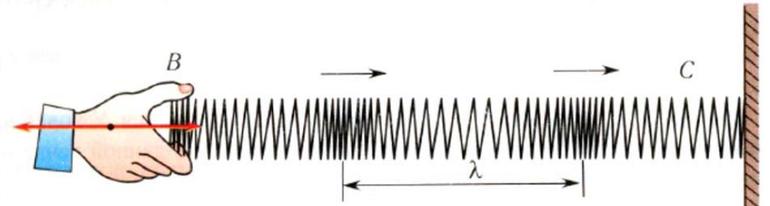
в чем состоит теорема о кинетической энергии

§ 44. РАБОТА СИЛ, ПРИЛОЖЕННЫХ К ТЕЛУ, И ИЗМЕНЕНИЕ ЕГО СКОРОСТИ. Вопросы

1. Что такое кинетическая энергия?

1. Кинетическая энергия тела равна произведению массы тела на квадрат его скорости, деленному пополам.

2. В чем состоит теорема о кинетической энергии?

2. Работа силы (равнодействующей сил) равна изменению кинетической энергии тела.

3. Как изменяется кинетическая энергия тела, если сила, приложенная к нему, совершает положительную работу? Отрица-тельную работу?

3. Кинетическая энергия тела растет, если сила, приложенная к телу совершает положительную работу и уменьшается, если сила совершает отрицательную работу.

4. Изменяется ли кинетическая энергия тела при изменении направления вектора его скорости?

5. Два шара одинаковой массы катятся навстречу друг другу с одинаковыми по модулю скоростями по очень гладкой поверхности. Шары сталкиваются, на мгновение останавливаются, после чего движутся в противоположных направлениях с такими же по модулю скоростями. Чему равна их общая кинетическая энергия до столкновения, в момент столкновения и после него?

5. Общая кинетическая энергия до столкновения:

в момент столкновения V₁=V₂=0, следовательно: Е_к=0. После столкновения

Источник

Кинетическая и потенциальная энергии

Кинетическая энергия

Работа всех сил, действующих на тело, равна работе равнодействующей силы.

Как видим, работа, совершенная силой, пропорционально изменению квадрата скорости тела.

Определение. Кинетическая энергия

Кинетическая энергия тела равна половине произведения массы тела на квадрат его скорости.

Теорема о кинетической энергии

Вновь обратимся к рассмотренному примеру и сформулируем теорему о кинетической энергии тела.

Теорема о кинетической энергии

Работа приложенной к телу силы равна изменению кинетической энергии тела. Данное утверждение справедливо и тогда, когда тело движется под действием изменяющейся по модулю и направлению силы.

Чтобы остановить тело, нужно совершить работу

Потенциальная энергия

Например, тело поднято над поверхностью земли. Чем выше оно поднято, тем больше будет потенциальная энергия. Когда тело падает вниз под действием силы тяжести, эта сила совершает работу. Причем работа силы тяжести определяется только вертикальным перемещением тела и не зависит от траектории.

Вообще о потенциальной энергии можно говорить только в контексте тех сил, работа которых не зависит от формы траектории тела. Такие силы называются консервативными.

Примеры консервативных сил: сила тяжести, сила упругости.

Когда тело движется вертикально вверх, сила тяжести совершает отрицательную работу.

При этом сила тяжести совершила работу, равную

Определение. Потенциальная энергия

Можно говорить о потенциальной энергии в поле силы тяжести, потенциальной энергии сжатой пружины и т.д.

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

Ясно, что потенциальная энергия зависит от выбора нулевого уровня (начала координат оси OY). Подчеркнем, что физический смысл имеет изменение потенциальной энергии при перемещении тел друг относительно друга. При любом выборе нулевого уровня изменение потенциальной энергии будет одинаковым.

При расчете движения тел в поле гравитации Земли, но на значительных расстояниях от нее, во внимание нужно принимать закон всемирного тяготения (зависимость силы тяготения от расстояния до цента Земли). Приведем формулу, выражающую зависимость потенциальной энергии тела.

Потенциальная энергия пружины

При этом работа силы упругости при изменении длины пружины на x в обоих случаях была одинакова и равна

Величина E у п р = k x 2 2 называется потенциальной энергией сжатой пружины. Она равна работе силы упругости при переходе из данного состояния тела в состояние с нулевой деформацией.

Источник

Теорема кинетической энергии. Доказательство

Теорема кинетической энергии. Доказательство

Такое уравнение уже встречалось в упражнении 6 ференциальное уравнение кривых, касательные к которым являются прямыми нулевого момента. Людмила Фирмаль

Важно отметить, что работа внутренних сил никуда не исчезает. С этим можно соврать Пожалуйста, проверьте напрямую. Действие На самом деле, рассмотрим 2 пункта и И и Рисунок 189 на расстоянии S НИИ р от. Действие м. На M представляет собой некую силу, S Он направлен вдоль LS и наоборот. Действие AG и g имеет равные силы И первый прямо opposite. As упоминалось ранее Рисунок 189. Wii 88 то, что мы называем взаимной властью 2 точки действия F, суммарная величина обеих сил, в зависимости от того, попадут ли точки отскока в знак плюс или минус В оригинале сумма 2mt 2 живых сил различных точек называется суммарной живой силой Лейбниц. Примечание, перевод или привлек.

Проверим непосредственно, что интеграл кинетической энергии действительно является следствием уравнений Лагранжа. Людмила Фирмаль

Таким образом, изменение кинетической энергии за период t tQ будет равно сумме работы всех сил, приложенных как к внешней, так и к внутренней системе. Внимание к твердым частицам. Если система является твердым телом в том смысле, который установлен в теоретической механике, то есть системой, в которой все точки находятся на определенном расстоянии друг от друга, то сумма основных действий всех внутренних сил равна zero. In факт, так как в этом случае расстояние r постоянно drA = 0 и iFjkdrjk Q.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Концепция и классификация

Ещё в древности энергию определяли как свойство или способность, которые тела и вещества должны производить вокруг себя и которые во время преобразований обмениваются через два механизма: в форме работы или тепла. Правда, тогда еще не знали, что таким образом выполняется закон сохранения энергии. Но кроме физических изменений, проявляющихся, например, в подъёме объекта, его транспортировке, деформации или нагревании, энергия также присутствует в химических изменениях, таких как сжигание куска дерева или разложение воды электрическим током.

Энергия — это способность тела работать, а также сила, которая выполняет работу. Она может быть представлена в виде различных переходных форм:

В физике самая важная форма называется механической энергией. Это сумма и определение потенциальной и кинетической энергии, формула которой: E = Ek + Wp.

Энергия движения

Кинетическая энергия тела — это та, которой тело обладает благодаря своему движению. Её определяют как силу, необходимую для ускорения тела определённой массы от покоя до максимальной указанной скорости. Как только достигается ускорение, тело сохраняет энергию, если скорость не изменяется. Чтобы тело вернулось в состояние покоя, необходима отрицательная работа той же величины.

Единица измерения кинетической энергии — джоуль. Обычно она обозначается буквой E c или E k. Расчёт мощности измеряется по-разному. Для того чтобы найти её количество можно использовать онлайн-калькулятор.

История и определение

Прилагательное «кинетический» в названии произошло от древнегреческого слова кίνησις kinēsis, что означает «движение».

Идею связи классической механики и кинематической энергии впервые выдвинули Готфрид Вильгельм Лейбниц и Даниэль Бернулли. Учёный Грейвсанд из Нидерландов предоставил экспериментальное подтверждение этой связи.

Но первые теоретические выкладки этих идей приписаны Гаспар-Гюстав Кориолису, который в 1829 году опубликовал статью, где была изложена математика этого процесса. Сам термин появился в 1849 году благодаря Уильяму Томсону, более известному как лорд Кельвин.

Теорема о кинетической энергии гласит: изменение кинетической силы тела равно работе равнодействующей всех сил, действующих на тело. Эта теорема справедлива независимо от того, какие силы действуют на тело.

Часто различают кинетическую силу поступательного и вращательного движения. Как и любая физическая величина, которая является функцией скорости, она не только зависит от внутренней природы этого объекта, но также зависит от отношений между объектом и наблюдателем (в физике наблюдатель формально определяется классом определённая система координат, называемая инерциальной системой отсчёта).

Эта энергия деградирует и сохраняется в каждой трансформации, теряя способность совершать новые трансформации, но она не может быть создана или разрушена, только трансформирована, поэтому её сумма во вселенной всегда постоянна.

Кинематика системы частиц

Для частицы или для твёрдого тела, которое не вращается, кинетическая энергия падает до нуля, когда тело останавливается. Однако для систем, которые содержат много частиц с независимыми движениями, это не совсем верно.

Для твёрдого тела, которое вращается, полная кинетическая сила может быть разбита на две суммы: энергия перемещения, связанная со смещением центра масс тела в пространстве, и вращения (с вращательным движением с определённой угловой скоростью).

Потенциальная энергия

Этот термин был введён в XIX веке учёным Уильямом Ренкином и связан с механической энергией, которая зависит от расположения тела в силовом поле (гравитационное, электростатическое и т. д. ) или с наличием силового поля внутри тела.

Теорема о потенциальной энергии утверждает, что она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень. Работа силы тяжести равна изменению потенциальной энергии тела, взятому с противоположным знаком.

Независимо от силы, её порождающей, потенциальная энергия, которой обладает физическая система, хранится благодаря своему положению и / или конфигурации, в чём и заключается её различие с кинетической энергией.

Значение потенциала всегда зависит от нахождения или конфигурации, выбранной для её измерения, поэтому иногда говорят, что физически имеет значение только его изменение отношений между двумя конфигурациями.

Потенциальная энергия присутствует не только в классической физике, но также в релятивистской и квантовой физике. Эта концепция также была распространена на физику элементарных частиц.

Смысл потенциальной силы связан с работой, выполняемой силами физической системы для перемещения её из одного состояния в другое. А её функция будет существенно зависеть от типа силового поля или взаимодействия, действующего на систему.

Это относится, например, к атомной физике при получении электронных состояний атома или к молекулярной физике для получения таких состояний молекулы, как:

В других более общих формулировках физики потенциальная функция также играет важную роль. Среди них лагранжева и гамильтонова формулировки механики.

Гравитационная сила

Потенциальной гравитацией обладают тела в силу того, что они имеют массу и находятся на определённом взаимном расстоянии. Среди огромных масс действуют силы притяжения. Применительно, например, к планетарному движению, основная масса солнечной системы состоит из массы Солнца, которая создаёт гравитационное силовое поле, воздействующее на малые массы планет. В свою очередь, каждая планета создаёт такое же поле, которое воздействует на второстепенные тела, находящиеся на её поверхности. Зависимость силы тяжести от высоты можно изобразить на графике. При увеличении массы тела линейно увеличивается и она.

Энергия упругой деформации

Эластичность — это свойство определённых материалов, благодаря которому, будучи деформированными, растянутыми или отделёнными от своего исходного положения, они могут восстановить своё первоначальное состояние или равновесие. Восстановительными силами, ответственными за восстановление, являются силы упругости, как в случае пружин, резиновых полос или струн музыкальных инструментов.

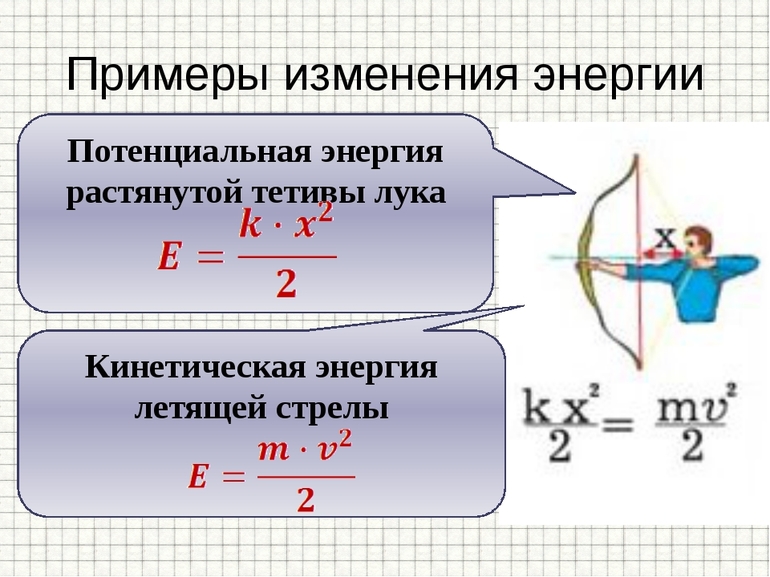
Многие древние военные машины использовали эти силы для запуска объектов на расстоянии, таких как дуга, которая стреляет стрелой, арбалет или катапульта. Вибрации или колебания материальных объектов, вызванные упругими силами, являются источником звуковых волн. Силы восстановления, когда объект восстанавливает свою первоначальную форму практически без какого-либо демпфирования или деформации, являются консервативными, и может быть получена упругая сила.

Пружина является примером упругого объекта, который точно восстанавливает первоначальную форму: при растяжении он создаёт упругую силу, стремящуюся вернуть его к первоначальной длине. Экспериментально подтверждено, что эта восстановительная сила пропорциональна растянутой длине пружины. Способ выразить эту пропорциональность между силой и растянутой суммой — через закон Гука.

Коэффициент пропорциональности при этой деформации зависит от типа материала и рассматриваемой геометрической формы. Для твёрдых тел сила упругости обычно описывается в терминах величины деформации, вызванной растягивающей силой, возникающей в результате этого растяжения, называемого упругостью или модулем Юнга. Для жидкостей и газов это выражается изменением давления, способного вызвать изменение объёма, и называется модулем сжимаемости.

Одним из свойств упругости твёрдого тела или жидкости при растяжении или деформации является то, что растяжение или деформация пропорциональны приложенному усилию. То есть для создания двойного растяжения потребуется двойная сила. Эта линейная зависимость смещения от приложенной силы известна как закон Гука.

Прикладное значение

Потенциальная электростатическая энергия может храниться с помощью конденсаторов. Конденсатор — это устройство, которое накапливает её внутри. Чтобы сохранить электрический заряд, он использует две проводящие поверхности, как правило, в форме листов или пластин, разделённых диэлектрическим материалом (изолятором). Эти платы являются электрически заряженными при подключении к источнику питания.

Две пластины имеют одинаковую величину, но с разными знаками, причём величина нагрузки пропорциональна приложенной разности потенциалов. Константа пропорциональности между зарядом, приобретённым конденсатором, и разностью потенциалов, достигнутой между двумя пластинами, называется ёмкостью конденсатора:

Области применения конденсаторов многочисленны в области электроники, и, следовательно, они также предназначены для бытовых приборов. В современных технологических приложениях их используют:

В этих применениях современной технологии конденсаторы способны накапливать электростатическую энергию в течение коротких периодов времени и с не слишком высокими значениями.

Источник

Учебники

Журнал «Квант»

Общие

Содержание

Механическая энергия

Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.

Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например: механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и др.

Энергия подчиняется закону сохранения, который является одним из важнейших законов природы.

Механическая энергия Е характеризует движение и взаимодействие тел и является функцией скоростей и взаимного расположения тел. Она равна сумме кинетической и потенциальной энергий.

Кинетическая энергия

Рассмотрим случай, когда на тело массой m действует постоянная сила \(

\vec F\) (она может быть равнодействующей нескольких сил) и векторы силы \(

\vec F\) и перемещения \(

\vec s\) направлены вдоль одной прямой в одну сторону. В этом случае работу силы можно определить как A = F∙s. Модуль силы по второму закону Ньютона равен F = m∙a, а модуль перемещения s при равноускоренном прямолинейном движении связан с модулями начальной υ₁ и конечной υ₂ скорости и ускорения а выражением \(

Отсюда для работы получаем

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела.

Кинетическая энергия обозначается буквой E_k.

Тогда равенство (1) можно записать в таком виде:

Теорема о кинетической энергии

работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела.

Так как изменение кинетической энергии равно работе силы (3), кинетическая энергия тела выражается в тех же единицах, что и работа, т. е. в джоулях.

Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения υ, то работа силы равна конечному значению кинетической энергии тела:

Физический смысл кинетической энергии

кинетическая энергия тела, движущегося со скоростью υ, показывает, какую работу должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

Потенциальная энергия

Потенциальная энергия – это энергия взаимодействия тел.

Потенциальная энергия поднятого над Землей тела – это энергия взаимодействия тела и Земли гравитационными силами. Потенциальная энергия упруго деформированного тела – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Потенциальными называются силы, работа которых зависит только от начального и конечного положения движущейся материальной точки или тела и не зависит от формы траектории.

При замкнутой траектории работа потенциальной силы всегда равна нулю. К потенциальным силам относятся силы тяготения, силы упругости, электростатические силы и некоторые другие.

Силы, работа которых зависит от формы траектории, называются непотенциальными. При перемещении материальной точки или тела по замкнутой траектории работа непотенциальной силы не равна нулю.

Потенциальная энергия взаимодействия тела с Землей

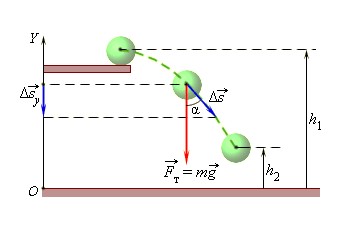
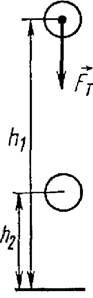
Найдем работу, совершаемую силой тяжести F_т при перемещении тела массой m вертикально вниз с высоты h₁ над поверхностью Земли до высоты h₂ (рис. 1). Если разность h₁ – h₂ пренебрежимо мала по сравнению с расстоянием до центра Земли, то силу тяжести F_т во время движения тела можно считать постоянной и равной mg.

Так как перемещение совпадает по направлению с вектором силы тяжести, работа силы тяжести равна

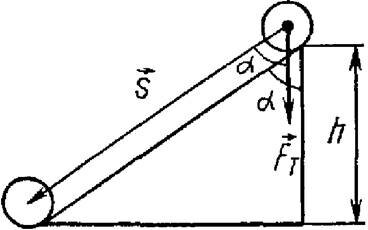
Рассмотрим теперь движение тела по наклонной плоскости. При перемещении тела вниз по наклонной плоскости (рис. 2) сила тяжести F_т = m∙g совершает работу

где h – высота наклонной плоскости, s – модуль перемещения, равный длине наклонной плоскости.

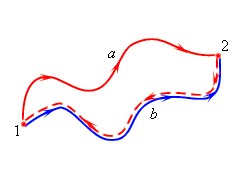
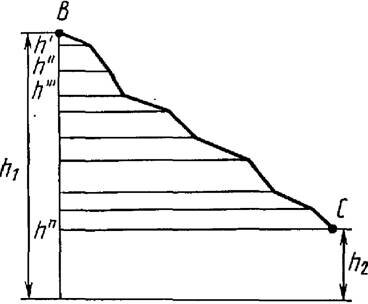
Движение тела из точки В в точку С по любой траектории (рис. 3) можно мысленно представить состоящим из перемещений по участкам наклонных плоскостей с различными высотами h’, h’’ и т. д. Работа А силы тяжести на всем пути из В в С равна сумме работ на отдельных участках пути:

где h₁ и h₂ – высоты от поверхности Земли, на которых расположены соответственно точки В и С.

Равенство (7) показывает, что работа силы тяжести не зависит от траектории движения тела и всегда равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.

При движении вниз работа силы тяжести положительна, при движении вверх – отрицательна. Работа силы тяжести на замкнутой траектории равна нулю.

Равенство (7) можно представить в таком виде:

Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.

Работа силы тяжести при перемещении тела массой m из точки, расположенной на высоте h₂, в точку, расположенную на высоте h₁ от поверхности Земли, по любой траектории равна изменению потенциальной энергии взаимодействия тела и Земли, взятому с противоположным знаком.

Потенциальная энергия обозначается буквой Е_p.

Значение потенциальной энергии тела, поднятого над Землей, зависит от выбора нулевого уровня, т. е. высоты, на которой потенциальная энергия принимается равной нулю. Обычно принимают, что потенциальная энергия тела на поверхности Земли равна нулю.

При таком выборе нулевого уровня потенциальная энергия Е_p тела, находящегося на высоте h над поверхностью Земли, равна произведению массы m тела на модуль ускорения свободного падения g и расстояние h его от поверхности Земли:

Физический смысл потенциальной энергии взаимодействия тела с Землей

потенциальная энергия тела, на которое действует сила тяжести, равна работе, совершаемой силой тяжести при перемещении тела на нулевой уровень.

В отличие от кинетической энергии поступательного движения, которая может иметь лишь положительные значения, потенциальная энергия тела может быть как положительной, так и отрицательной. Тело массой m, находящееся на высоте h, где h \(

Потенциальная энергия гравитационного взаимодействия

Потенциальная энергия гравитационного взаимодействия системы двух материальных точек с массами m и М, находящихся на расстоянии r одна от другой, равна

где G – гравитационная постоянная, а нуль отсчета потенциальной энергии (Е_p = 0) принят при r = ∞.

Потенциальная энергия гравитационного взаимодействия тела массой m с Землей, где h – высота тела над поверхностью Земли, M_e – масса Земли, R_e – радиус Земли, а нуль отсчета потенциальной энергии выбран при h = 0.

При том же условии выбора нуля отсчета потенциальная энергия гравитационного взаимодействия тела массой m с Землей для малых высот h (h « R_e) равна

g = G \cdot \frac\) – модуль ускорения свободного падения вблизи поверхности Земли.

Потенциальная энергия упруго деформированного тела

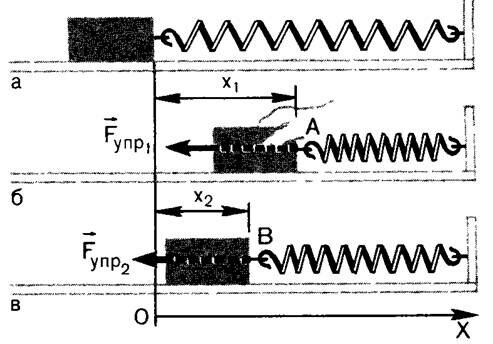
Вычислим работу, совершаемую силой упругости при изменении деформации (удлинения) пружины от некоторого начального значения x₁ до конечного значения x₂ (рис. 4, б, в).

Сила упругости изменяется в процессе деформации пружины. Для нахождения работы силы упругости можно взять среднее значение модуля силы (т.к. сила упругости линейно зависит от x) и умножить на модуль перемещения:

Физическая величина, равная половине произведения жесткости тела на квадрат его деформации, называется потенциальной энергией упруго деформированного тела:

Из формул (14) и (15) следует, что работа силы упругости равна изменению потенциальной энергии упруго деформированного тела, взятому с противоположным знаком:

Если x₂ = 0 и x₁ = х, то, как видно из формул (14) и (15),

Физический смысл потенциальной энергии деформированного тела

потенциальная энергия упруго деформированного тела равна работе, которую совершает сила упругости при переходе тела в состояние, в котором деформация равна нулю.

Закон сохранения энергии в механических процессах

Потенциальная энергия характеризует взаимодействующие тела, а кинетическая энергия – движущиеся тела. И потенциальная, и кинетическая энергия изменяются только в результате такого взаимодействия тел, при котором действующие на тела силы совершают работу, отличную от нуля. Рассмотрим вопрос об изменениях энергии при взаимодействиях тел, образующих замкнутую систему.

Замкнутая система – это система, на которую не действуют внешние силы или действие этих сил скомпенсировано. Если несколько тел взаимодействуют между собой только силами тяготения и силами упругости и никакие внешние силы на них не действуют, то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии тел, взятому с противоположным знаком:

По теореме о кинетической энергии, работа тех же сил равна изменению кинетической энергии:

Из сравнения равенств (17) и (18) видно, что изменение кинетической энергии тел в замкнутой системе равно по абсолютному значению изменению потенциальной энергии системы тел и противоположно ему по знаку:

Закон сохранения энергии в механических процессах:

сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и си-лами упругости, остается постоянной.

Сумма кинетической и потенциальной энергии тел называется полной механической энергией.

Основное содержание закона сохранения энергии заключается не только в установлении факта сохранения полной механической энергии, но и в установлении возможности взаимных превращений кинетической и потенциальной энергии тел в равной количественной мере при взаимодействии тел.

Приведем простейший опыт. Подбросим вверх стальной шарик. Сообщив начальную скорость υ_нач, мы придадим ему кинетическую энергию, из-за чего он начнет подниматься вверх. Действие силы тяжести приводит к уменьшению скорости шарика, а значит, и его кинетической энергии. Но шарик поднимается выше и выше и приобретает все больше и больше потенциальной энергии (Е_p = m∙g∙h). Таким образом, кинетическая энергия не исчезает бесследно, а происходит ее превращение в потенциальную энергию.

В момент достижения верхней точки траектории (υ = 0) шарик полностью лишается кинетической энергии (Е_k = 0), но при этом его потенциальная энергия становится максимальной. Дальше шарик меняет направление движения и с увеличивающейся скоростью движется вниз. Теперь происходит обратное превращение потенциальной энергии в кинетическую.

Закон сохранения энергии раскрывает физический смысл понятия работы:

работа сил тяготения и сил упругости, с одной стороны, равна увеличению кинетической энергии, а с другой стороны, – уменьшению потенциальной энергии тел. Следовательно, работа равна энергии, превратившейся из одного вида в другой.

Закон об изменении механической энергии

Если система взаимодействующих тел не замкнута, то ее механическая энергия не сохраняется. Изменение механической энергии такой системы равно работе внешних сил:

где Е и Е₀ – полные механические энергии системы в конечном и начальном состояниях соответственно.

Примером такой системы может служить система, в которой наряду с потенциальными силами действуют непотенциальные силы. К непотенциальным силам относятся силы трения. В большинстве случаев, когда угол между силой трения F_tr и элементарным перемещением Δr тела составляет π радиан, работа силы трения отрицательна и равна

где s₁₂ – путь тела между точками 1 и 2.

Силы трения при движении системы уменьшают ее кинетическую энергию. В результате этого механическая энергия замкнутой неконсервативной системы всегда уменьшается, переходя в энергию немеханических форм движения.

Например, автомобиль, двигавшийся по горизонтальному участку дороги, после выключения двигателя проходит некоторый путь и под действием сил трения останавливается. Кинетическая энергия поступательного движения автомобиля стала равной нулю, а потенциальная энергия не увеличилась. Во время торможения автомобиля произошло нагревание тормозных колодок, шин автомобиля и асфальта. Следовательно, в результате действия сил трения кинетическая энергия автомобиля не исчезла, а превратилась во внутреннюю энергию теплового движения молекул.

Закон сохранения и превращения энергии

при любых физических взаимодействиях энергия превращается из одной формы в другую.

Иногда угол между силой трения F_tr и элементарным перемещением Δr равен нулю и работа силы трения положительна:

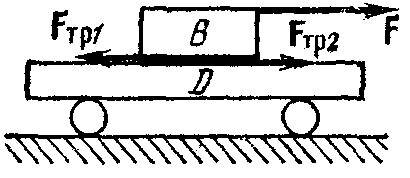
Пример 1. Пусть, внешняя сила F действует на брусок В, который может скользить по тележке D (рис. 5). Если тележка перемещается вправо, то работа силы трения скольжения F_tr2, действующей на тележку со стороны бруска, положительна:

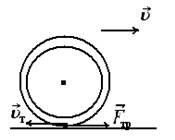
Пример 2. При качении колеса его сила трения качения направлена вдоль движения, так как точка соприкосновения колеса с горизонтальной поверхностью двигается в направлении, противоположном направлению движения колеса, и работа силы трения положительна (рис. 6):

Литература

Составители

Варахобова Анна (11 «А», МГОЛ № 1, 2008 г.)

Источник