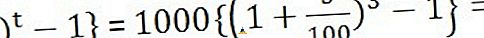в чем состоит принципиальная разница между простыми и сложными процентами
Сложный процент против простого процента
Содержание:
Сравнительная таблица
Что такое простой процент?
Формула простого процента
Математическая формула для расчета простых процентов:
Что такое сложные проценты?
Простые проценты редко используются в обычных займах и депозитах из-за временной стоимости денег. Когда проценты, полученные за определенный период, добавляются к основной сумме долга, это называется компаундирование. Это означает, что в следующем периоде проценты начисляются на новую (более высокую) сумму, а не на первоначальную сумму. Фактически, основная сумма долга увеличивается по мере начисления процентов, что приводит к еще большему процентному доходу. В течение длительного периода времени это оказывает огромное влияние на прибыль. Это явление называется магия сложения и дополнительно поясняется в примере ниже.
Формула сложных процентов
Математический способ расчета сложных процентов:
Обратите внимание: поскольку это экспоненциальная функция, сумма увеличивается нелинейно, когда продолжительность инвестиций (п) увеличивается.
Пример простого и сложного процента
Допустим, вы внесли 10 000 долларов и хранили их в банке в течение 10 лет, имея процентную ставку 10%. Если вы зарабатываете 10% простых процентов каждый год, вы закончите 10 лет с общим процентным доходом в размере 10 000 долларов (I = 10 000 x 0,10 x 10).
Однако, если бы проценты были сложными, процентный доход в каждом году был бы выше, чем в предыдущем году. А по истечении 10 лет вы бы заработали 15 937 долларов в виде процентов.
Почему взимаются проценты?
При заимствовании денег не всегда начисляются проценты. Например, при займе у друзей, родителей или других родственников кредитор может не требовать процентов. Однако есть несколько причин для обоснованного начисления процентов, в том числе:
Ставка процента зависит от всех этих факторов, но обычно существуют законы о ростовщичестве, которые запрещают взимать проценты выше определенной ставки. На протяжении всей истории существовало множество законов и религиозных запретов на ростовщичество.
Введение в финансовую математику
Учебное пособие содержит введение в финансовую математику. Оно описывает, что такое платежи, какие бывают процентные ставки наращения и дисконта, сложных и простых процентов, их связь, как рассчитывают стоимость потоков платежей, внутреннюю норму доходности, что такое аннуитет и другие вопросы. Книга будет полезна как студентам и аспирантам, изучающим финансовую математику, рассчитывающим доходность кредитов, банковских вкладов и инвестиционных проектов, так и специалистам-практикам, которые смогут найти в ней ответы на практические вопросы.
Оглавление
Приведённый ознакомительный фрагмент книги Введение в финансовую математику предоставлен нашим книжным партнёром — компанией ЛитРес.
2. Простые и сложные проценты
Обычно процентный доход выражается не в виде конкретной суммы I, а с помощью так называемой процентной ставки i. Ставка i используется как некоторый показатель, индикатор, применимый для множества различных ситуаций и позволяющий проводить сравнения, что объясняет удобство его использования.
Простые и сложные проценты
Исторически сложилось два разных вида используемых процентов: простые и сложные.
Простые проценты представляют собой равномерный по времени способ начисления процентного дохода на первоначальную сумму кредита:
Процентный доход прямо пропорционален сроку кредита:
Такие проценты являются наиболее простыми и исторически возникли первыми. Но если срок рассматриваемого кредита велик (например, составляет несколько лет), то возникает следующий вопрос. По прошествии года кредитор уже получил право на получение процентного дохода за прошедший год. Но согласно условиям сделки фактического получения этих денежных средств нужно ждать еще n — 1 лет. Значит, на эти денежные средства также должны начисляться проценты. Таким образом, по истечении двух лет кредитор должен получить
Рассуждая аналогично получим, что через n лет наращенная сумма составит:
Это и есть формула начисления сложных процентов. Их основным отличием от простых процентов является начисление процентов на уже начисленные за прошедшие периоды проценты. Присоединение процентов к основной сумме долга для дальнейшего наращения называется капитализацией.
Годовая процентная ставка
В приведенных выше формулах процентная ставка i предполагается годовой, т.е. срок необходимо выражать в годах.
Процентная ставка всегда считается годовой, если не указано противное.
Отметим, что при рассмотрении сложных процентов выше считалось, что они начисляются один раз в год (после истечения года, собственно, их можно капитализировать). Начисление сложным процентов считается начислением один раз в год, если не указано противное.
Нецелые значения срока
В формулах наращения простых и сложных процентов срок n может быть как целым числом (целое число лет), так и нецелым.
Действительно, для простых процентов процентных доход прямо пропорционален сроку. Соответственно, срок может быть любым: год, полтора, любая доля года и др.
Для сложных процентов нецелое число лет является логичным обобщением концепции капитализации. Например, срок в 2,5 года означает два полных года и еще половину, то есть два годовых начисления процентов и еще одно «половинное» начисление по истечении полугода.
Сравнение простых и сложных процентов
Предположим, что выдаются два кредита с одинаковой начальной суммой P и одинаковой процентной ставкой i на одинаковый срок n лет, но для первого кредита проценты начисляются по формуле простых процентов, а для второго — по формуле сложных процентов. Давайте сравним суммы начисленного процентного дохода.
Для простых процентов функция
представляет собой линейную функцию от n, а для сложных:
Сделаем иллюстративной расчет для случая P = 100 руб., различных сроков n и значений процентной ставки i. Полученные значения наращенной суммы S приведены в Таблице 1.
Изучив таблицу, легко увидеть, что при сроке меньше года наращенная сумма при расчете по формуле простых процентов превышает наращенную сумму при расчете по формуле сложных процентов, а при сроке более года — наоборот.
Для полного понимания изобразим на Рис. 1 график зависимости S(n) для сложных и простых процентов.
Из графика видно, что при сроке меньше года простые проценты превышают сложные, а при сроке более года — наоборот. Пользуясь этим, банки иногда в кредитных договорах устанавливают начисление процентов по формуле простых процентов при сроках до года и по формуле сложных процентов — в остальных случаях.
Различные процентные ставки
Процентная ставка рассматриваемого кредита может быть как фиксированной (постоянной), так и переменной, в зависимости от условий договора. Примером переменной ставки является ставка вида «LIBOR 1 + 1,5%». Ставки такого рода часто применяются на западных рынках. Произведем расчет наращенной суммы в случае переменной ставки.
Предположим, что ставка кредита меняется в течение его срока. Пусть полный срок кредита n разбит на периоды длины n1,…, nk лет, причем в течение первого периода действовала процентная ставка i1, в течение второго периода — i2,…, в течение k-ого периода — ik.
Тогда в случае расчета по формуле простых процентов процентный доход за промежуток времени n1 будет:
В итоге наращенная сумма составит:
Из полученной формулы можно сделать следующие выводы. Размер наращенной суммы не зависит от порядка чередования периодов с различными процентными ставками. Кроме того, если в два или более периода имело место одна и та же процентная ставка, то для целей расчета наращенной суммы их можно объединить в один период, длительность которого равна сумме длительностей исходных.
Формулу можно переписать еще и так:
где νm = nm / n — доля промежутка nm в полном сроке n рассматриваемого кредита. Получается, что для случая с переменной процентной ставкой можно ввести понятие эффективной процентной ставки простых процентов (см. об эффективных ставках подробнее ниже)
рассчитываемой как взвешенная сумма процентных ставок каждого периода. Эту ставку можно использовать как единый эквивалент для расчета наращенной суммы:
Теперь перейдем к аналогичному расчету с использованием методики сложных процентов. По истечении первого периода n1 наращенная сумма составит:
Поскольку сложные проценты начисляются на капитализированную сумму, после второго периода n2 наращенная сумма составит:
После k-ого периода nk найдем требуемую наращенную сумму:
Из полученной формулы можно сделать следующие выводы, аналогичные тем, что были сделаны ранее для простых процентов: размер наращенной суммы не зависит от порядка чередования периодов с различными процентными ставками. Кроме того, если в два или более периода имело место одна и та же процентная ставка, то для целей расчета наращенной суммы их можно объединить в один, длительность которого равна сумме длительностей исходных промежутков.
Аналогично предыдущему можно ввести понятие эффективной ставки сложных процентов (см. подробнее об этом ниже):
Здесь νr = nr / n — доля промежутка nr в полном сроке рассматриваемого кредита. Получается, что для случая с переменной процентной ставкой можно ввести понятие эффективной процентной ставки сложных процентов, рассчитываемой как взвешенное произведение процентных ставок каждого периода, и которую можно использовать как единый эквивалент для расчета наращенной суммы:
Сложные проценты с начислением чаще, чем раз в год
Во всех рассуждениях ранее при использовании сложных процентов предполагалось, что они начисляются один раз в год. Однако на практике встречаются случаи, когда начисление происходит чаще. Пусть оно происходит m раз в год, где m — натуральное число. Например, начисление может происходить ежемесячно (m = 12).
Для сложных процентов с начислением один раз в год была получена формула:
Теперь мысленно предположим, что в рассуждениях, из которых была выведена эта формула, период времени «год» будет заменен на период времени «1/m года» или «m-ая доля года». Поскольку все рассуждения останутся в силе, получим формулу:
где if — процентная ставка за «m-ую часть года», nf — срок, отраженный в «m-ых частях года» (а не в годах, как ранее). Для того, чтобы вернуться к используемым ранее обозначениям выразим if и nf через годовые переменные:
Последнее соотношение легко интерпретируемо: при сроке n лет количество периодов размером «1/m года» равно mn.
Тогда с использованием годовой процентной ставки итоговую формулу расчета наращенной суммы с использованием сложных процентов с начислением m раз в год можно записать как:
Поскольку, как было выяснено, формула сложных процентов с начислением m раз в год верна и для нецелого числа лет n, то и полученная формула верна для нецелого n. Более того, можно показать, что она остается верной и для нецелого m.
Отметим, что всегда предполагается, что сложные проценты начисляются один раз в год, если не указано противное.
Дня того, чтобы продемонстрировать зависимость наращенной суммы от количества начислений m раз в год, сведем в Таблицы 2 и 3 результаты расчетов при Р = 100 руб. и ставке i = 10% в Таблице 2 и ставке i = 25% в Таблице 3.
Дискретное и непрерывное начисление процентов
Зададимся вопросом: как изменится формула начисления процентов, если увеличивать количество m начислений процентов в год.
Например, сначала предполагать, что m = 12, затем 24, 365 (ежедневное начисление), 365*24 (ежечасное) и др. При m, стремящемся к бесконечности, получим непрерывные проценты (проценты с непрерывным начислением):
Вспомним, что замечательный предел внутри скобок равен e. Тогда:
Обычно годовую ставку начисления непрерывных процентов обозначают δ. Итоговая формула непрерывных процентов выглядит как:
Разница между простым процентом и сложным процентом
Сравнительная таблица
| Основа для сравнения | Простой интерес | Сложный процент |
|---|---|---|
| Имея в виду | Простые проценты относятся к процентам, которые рассчитываются как процент от основной суммы. | Сложный процент относится к проценту, который рассчитывается как процент от основной суммы и начисленных процентов. |
| Вернуть | Меньше | Сравнительно высокий |
| принципал | постоянная | Продолжает меняться в течение всего периода заимствования. |
| рост | Остается однородным | Быстро увеличивается |
| Проценты начисляются на | принципал | Основной + накопленный интерес |
| формула | Простой интерес = P * r * n | Сложный процент = P * (1 + r) ^ nk |
Определение простого интереса
Формула : простой интерес = P × i × n
Где P = основная сумма
я = процентная ставка
n = количество лет
Например : если вы одолжите рупий. 1000 от вашего друга при 10% годовых в течение 3 лет, затем вы должны вернуть 1300 рупий своему другу в конце 3-го года 1000 рупий за основную сумму и рупий. 300 в качестве процентов, для хранения суммы при себе. Если мы сложим основную сумму и проценты, то она будет известна как сумма. Следует иметь в виду, что чем больше денег и периодов, тем выше будет процент.
Определение сложного процента
Временной интервал между двумя периодами выплаты процентов называется Периодом конверсии. В конце конверсионного периода проценты начисляются следующим образом:
| Период конверсии | Составленный |
|---|---|
| 1 день | Ежедневно |
| 1 неделя | еженедельно |
| 1 месяц | ежемесячно |
| 3 месяца | квартальный |
| 6 месяцев | Раз в полгода |
| 12 месяцев | ежегодно |
Обычно банки выплачивают проценты раз в полгода, но финансовые учреждения проводят политику выплаты процентов ежеквартально. Для вычисления сложного процента вы должны использовать эту формулу:
Формула : сложный процент = P
Где P = принципал
n = количество лет
я = процентная ставка за период
Ключевые различия между простым интересом и сложным интересом
Ниже приведены основные различия между простым и сложным интересом:
Видео: Простой против сложного интереса
пример
Предположим, Алекс депонировал рупий. 1000 в банк под 5% годовых (простой и составной) в год на 3 года. Узнайте общий интерес, который он получит в конце третьего года?
Решение : здесь P = 1000, r = 5% и t = 3 года
Заключение
Что такое сложный процент и в чем его выгода
Ставка считается главным показателем доходности вклада. Хотя стоит обратить внимание и на способ начисления процентов. Разберемся, в чем разница между простыми и сложными процентами, а также какой вариант и в каком случае будет более выгодным.
В чем разница между простым и сложным процентом.
Как рассчитывается сложный процент по вкладу, пример начисления.
Сравнительная таблица доходности по вкладу с простым и сложным начислением процентов.
В чем преимущества вклада со сложным процентом.
Для большинства граждан только один параметр является решающим при выборе вклада — ставка. Высокая ставка — хороший доход от размещения средств, думают многие. Но есть и другой момент, который влияет на конечную доходность, — вид начисляемых процентов. Простые — предлагают большинство банков, сложные (с капитализацией) — встречаются реже. Разберемся, какой вариант в итоге окажется более выгодным.
В чем разница между простым и сложным процентом
Не трудно подсчитать, что сложные проценты в итоге принесут больший доход. Ведь происходит начисление процентов на сумму вклада + начисленные ранее проценты. То есть доходность растет как снежный ком. И чем больше срок размещения средств, тем более ощутимая будет выгода.
Чтобы понять, какой именно вид процентов предусмотрен по конкретному вкладу, проверьте его параметры. У простых процентов выплаты периодические или в конце срока, капитализации нет. У сложных — раз в месяц/квартал, с капитализацией.
Как рассчитывается сложный процент по вкладу, пример начисления
Допустим, вы размещаете во вкладе 100 тыс. рублей под ставку 7% годовых на срок 3 месяца. Капитализация — раз в месяц. Ставку переводим из процентов в десятичную дробь (7/100). А период (31 день) делим на количество дней в году (365).
Рассчитаем доходность за первый месяц (31 день):
100 000 * (7/100) * (31/365) = 595 рублей
Доходность за второй месяц будет рассчитана на сумму 100 5956 то есть с учетом уже начисленных процентов. И составит:
(100 000 + 595) * (7/100) * (31/365) = 599 рублей
Доходность за третий месяц составит:
(100 595 + 599) * (7/100) * (31/365) = 602 рубля
Доходность за весь срок (три месяца) составит 1 796 рублей, а вкладчик получит на руки 101 796 рублей.
Для сравнения: если бы вкладчик разместил бы ту же сумму (под аналогичную ставку и на такой же срок), то получил бы 1785 рублей дохода (на 11 рублей меньше, чем по вкладу с капитализацией). Разница при размещении на короткий срок не такая уж и большая. На длительные сроки перевес будет более ощутимым.
Сравнительная таблица доходности по вкладу с простым и сложным начислением процентов
Чтобы оценить выгоду разных схем на разные сроки, составим сравнительную таблицу. Сумма вклада 100 тыс. рублей, срок 1 год (12 месяцев), ставка — 12%. Капитализация по вкладу со сложным процентом — раз в месяц.
Таблица 1 «Сравнительная таблица доходности по вкладу с простым и сложным начислением процентов (при равных условиях)»
Простые и сложные проценты в банках. Где выгода?
Открывая банковский вклад нужно обращать внимание не только на размер процентной ставки, но и на вид начисления процентов. Бывает простое начисление процентов и сложное. В этой статье мы разберем разницу между видом начисления процентной ставки, а также определим в чем выгода того или иного способа начисления.
В чем разница между простыми и сложными процентами?
Обычно банки предлагают простое начисление процентов. Что это значит? Это значит, что проценты будут начислены на ваш вклад только в конце срока. Т.е. допустим вы открыли вклад под 10% годовых и вложили 10 000 рублей. Через год вам будет начислено в виде процентов 1 000 рублей. Если вы оставите вклад на второй год, то по истечении этого срока вам будет начислена еще 1 000 рублей.
За 2 года, при простом начислении процентов ваша итоговая сумма составит: 12 000 рублей.
Итого, за 2 года при сложном начислении ваша сумма составит: 12 100 рублей
Думаю, нет смысла объяснять, что вы выберите: 12 000 или 12 100 рублей. К тому же дополнительным преимуществом сложным процентов является тот факт, что они также входят в систему страхования вкладов. Т.е. если у банка отзывают лицензию, то все начисленные проценты также подлежат возврату вкладчику.
При простом начислении, деньги выплачиваются только в конце срока, т.е. по факту они не были начислены, даже если до окончания вашего вклада оставался только один день! И в данном случае вы имеете право на возврат только основного капитала.
Особенно привлекательным становится вклад с ежемесячной или ежеквартальной капитализацией процентов. Чем ниже период капитализации по вкладу, тем более высокий доход он дает. Дело тут в кумулятивном эффекте. Когда на начисленные проценты в виде прибыли также начисляется прибыль. Иногда сложные проценты называют процентами с учетом реинвестирования или капитализации. Обращайте на это внимание когда заключаете договор с банком. Если в договоре сказано, что проценты начисляются в конце срока вклада, то речь идет о простом начислении процентов.
Банки не очень часто предлагаю реинвестирование процентов. Даже если проценты начисляются ежемесячно или ежеквартально, банки предпочитают не использовать полученную прибыль для начисления на них дополнительных процентов, а перечисляют на отдельный счет. Дело здесь, как было указано выше, в эффекте рефинансирования, когда эффективная процентная ставка за счет капитализации будет выше, первоначально заявленной банком.
Банки обычно указывают номинальную процентную ставку, поскольку эффективная процентная ставка при условии снятия процентов может и не случиться.
Формула расчета сложного процента по вкладам в банках
Для тех, кто хочет сам понять какую сумму он получит вложив деньги под сложный процент в банке есть специальная формула реинвестирования или капитализации вклада:
S=K * (1+r/t)™
Пример.
Вы открыли вклад на срок 2 года, под 12% годовых, капитализация процентов ежеквартальная. Вы внесли 10 000 рублей.
Какая сумма будет у вас в конце срока?
Получаем, S=10 000 * (1+0.12/4)∧8 = 12 668 рублей.
Итого за 2 года подобный вклад принесет вам 2 668 рублей или 26,68% доходности.
Если, для примера взять простое начисление процентов под те же 12% годовых на 2 года, с ежегодным начислением, но без капитализации, то в конце срока сумма будет немного меньше, а именно 2 400 рублей или 24% доходности.
Конечно, разница в 2,68% не такая уж и большая. Но все меняется если изменится сумма вклада в большую сторону или же увеличиться срок вклада. Именно на больших временных интервалах разница между простым и сложным начисление процентов наиболее заметна. На длительных интервалах времени разница в достигнутом результате может изменяться в разы. Недаром Ротшильды (богатейшее семейство планеты) называли сложные проценты «восьмым чудом света».
Поэтому, при поиске более выгодного вклада в банках, обращайте внимание на вид начисление процентов.
Для того, чтобы точно рассчитать проценты по депозитам с капитализацией, воспользуйтесь калькулятором доходности вкладов.