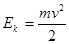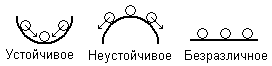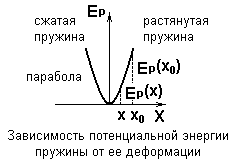в чем состоит принцип минимума потенциальной энергии

Принципы Материи. 4. Принцип минимума энергии

Все ПРИНЦИПЫ взаимосвязаны, дополняют друг друга и образуют нечто целое. Трудно выделить среди них главные. Если все же это сделать, то, скорее всего, главным является ПРИНЦИП МИНИМУМА ЭНЕРГИИ. Все процессы в Природе происходят с выполнением Принципа минимизации энергии, так как это повышает устойчивость системы. Каждая структура имеет минимально возможную для нее энергию, обеспечивающую устойчивость этой структуры. Принцип минимума энергии является своеобразным механизмом преобразования различных форм материи: избыточная энергия «консервируется» в виде вещества, связей новообразованных структур и энергетического поля (энергетической среды, в которой или с помощью которой происходит энергетический обмен в системах и поддержание стабильности). Если бы не было этой энергетической среды, то пришлось бы признать атом «вечным» двигателем. Энергия является носителем универсальной информации. Главным же носителем энергии и информации можно считать сегодня нейтрино – эти всепроникающие частицы, которые обеспечивают энергоинформационный обмен в любых условиях.

В живой Природе вы можете наглядно наблюдать этот принцип на примере животных: практически все животные минимизируют свои затраты энергии (кошки, например, порядка 20 часов спят или неподвижны). В живой Природе процессы окисления протекают медленно с минимальным выбросом энергии (плотность энергетического потока низкая). При этом выделившаяся энергия практически сразу используется следующим звеном системы. Микроорганизмы конечное и начальное звено. Они получают энергию как из живой Природы, так и неживой Природы. Биохимические окислительно-восстановительные процессы идут с минимальным выделением энергии.

Только человек не желает выполнять Принцип минимизации энергии. Все процессы в Техногенной Природе человека происходят с выбросами энергии с высокими плотностями потоков.

Источник

Принцип минимума потенциальной энергии

Если тела в начальном положении больше его в конечном положении, то работа потенциальной силы положительна. Состояние с меньшей потенциальной энергией является энергетически выгодным.

Принцип минимума : любая замкнутая система стремится перейти в такое состояние, в котором ее потенциальная энергия минимальна.

Кинетическая энергия –энергия движения, зависит от скорости тела, следовательно, ее значение зависит от выбора системы отсчета (т.е. относительная величина).

Кинетическая энергия тела массой m, движущегося со скоростью v, равна работе, которую совершает суммарная сила для сообщения покоящемуся телу этой скорости

Кинетическая энергия, как и работа, измеряется в джоулях (Дж).

Закон сохранения механической энергии:

Полная механическая энергия системы – сумма ее кинетической и потенциальной энергии .

Закон сохранения энергии: Полная механическая энергия замкнутой системы тел, между которыми действуют консервативные силы, остается постоянной. Взаимное превращение кинетической энергии в потенциальную и обратно в равных количествах. При этом полная энергия остается неизменной.

Под действием сил трения на опору механическая энергия тел превращается в кинетическую энергию хаотического движения атомов и молекул вещества, а также в потенциальную энергию их взаимодействия. Эта часть энергии называется внутренней.

С учетом изменения внутренней энергии закон сохранения энергии как всеобщий закон природы формулируется так: При любых процессах полная энергия изолированной системы не изменяется; энергия системы может только превращаться из одной формы в другую и перераспределяться между частями системы.

Источник

В чем состоит принцип минимума потенциальной энергии

9.7.8. Конечно-элементная формулировка плоской задачи теории упругости: вывод СЛАУ МКЭ

9.7.8.1. Принцип минимума потенциальной энергии

Согласно вариационному принципу Лагранжа полная потенциальная энергия тела, находящегося в равновесии под действием внешних объемных и поверхностных сил, достигает минимума на истинном поле перемещений, т.е. на поле перемещений, удовлетворяющем полной системе уравнений теории упругости. Отсюда следует, что вариация функционала энергии на истинных перемещениях должна быть равна нулю:

. (9.36)

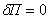
Поскольку полная потенциальная энергия тела складывается из потенциальной энергии деформации тела и работы внешних сил (5.1), то последнее соотношение (9.36) может быть записано следующим образом:

(9.37)

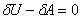
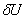
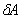
где — вариация потенциальной энергии деформации тела, — вариация работы внешних сил, совпадающая по своему виду с элементарной работой внешних сил на возможных перемещениях.

Вычислим первое слагаемое в формуле (9.37). В предыдущей лекции было отмечено, что потенциальная энергия деформации тела представляет собой интеграл по объему тела от удельной потенциальной энергии:

(9.38)

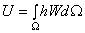
где W – удельная потенциальная энергия тела, или так называемый упругий потенциал.

Выражение упругого потенциала было получено в предыдущей лекции и в матричном виде может быть записано следующим образом:

(9.39)

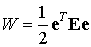
Как следует из соотношения ( 9.39) упругий потенциал представляет собой квадратичную форму относительно компонент вектора деформации. Запишем соотношение (9.39) в развернутом виде:

(9.40)

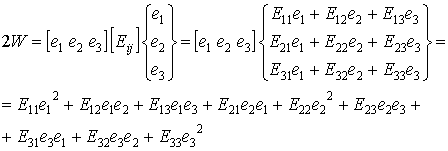
В данной формуле для сокращений записей были использованы индексные обозначения компонент вектора деформации:

(9.41)

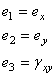
С учетом симметрии матрицы упругих модулей:

, (9.42)

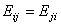
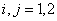
соотношение (6.5) может быть записано в виде квадратичной формы:

. (9.43)

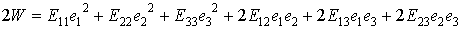
Применим теперь операцию варьирования к выражению потенциальной энергии деформации тела:

. (9.44)

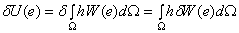
Отметим, что в данном случае потенциальная энергия является функцией деформаций, которые в свою очередь зависят от поля перемещений. Поэтому необходимо использовать правило варьирования сложной функции многих переменных:

, (9.45)

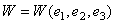
где перемещения являются независимыми варьируемыми функциями, а деформации – варьируемыми функциями, зависящими от перемещений.

Заметим также, что с формальной точки зрения математически операция вычисления вариации функции эквивалентна операции вычисления дифференциала функции, т.е. выполняется по тем же правилам:

(9.46)

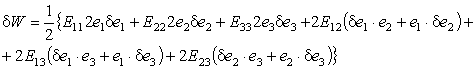
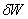
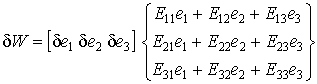
Перегруппировав слагаемые в соотношении (9.46), получим выражение в виде:

. (9.47)

Окончательно вариация упругого потенциала может быть записана в следующем матричном виде:

, (9.48)

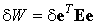
где 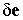— вариация вектора деформаций.

Тогда вариация потенциальной энергии деформации тела будет записана следующим образом:

. (9.49)

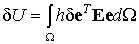
Вариация работы внешних сил находится простым варьированием соотношения (9.27) с учетом того, что варьируемой независимой функцией является поле перемещений:

, (9.50)

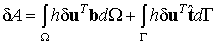
где 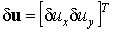— вариация вектора перемещений.

Заметим еще раз, что выражение (9.50) совпадает с выражением элементарной работы внешних сил на возможных перемещениях .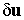

9.7.8.2. Вывод разрешающих уравнений

Согласно рассмотренному выше алгоритму конечно-элементной дискретизации область тела представляется в виде множества не пересекающихся подобластей. В соответствии с этим разбиением объемные и поверхностные интегралы, входящие в выражения потенциальной энергии и работы внешних сил, равны сумме интегралов по конечным элементам. Следовательно, интегральные соотношения (9.49) и (9.50) будут представлены в виде:

(9.51)

(9.52)

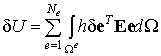
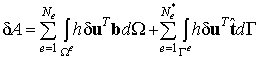
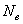
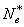
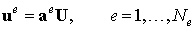
где — общее число конечных элементов, — число конечных элементов, выходящих на границу области.

. (9.53)

Когда формулы (5.6б) и (5.7б), представляющие собой перемещения и деформации в любой точке конечного элемента, могут быть представлены следующим образом:

(9.54)

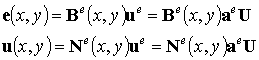
Соответственно вариации функций U и e вычисляются следующим образом:

, (9.55)

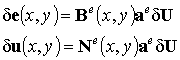
Применим операцию транспонирования к выражению (9.55). Согласно правилам вычисления транспонированной матрицы, представляющей собой произведение трех матриц, запишем:

(9.56)

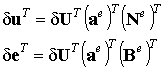
Подставим теперь выражения (9.56) и (9.54) в формулу вариации потенциальной энергии (9.51). Получим:

, (9.57)

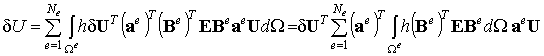
Введем следующие обозначения:

, (9.58)

, (9.59)

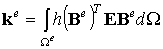
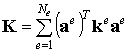
где k e называется элементной матрицей жесткости, K называется глобальной матрицей жесткости. В результате получим компактное матричное выражение потенциальной энергии тела:

. (9.60)

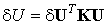
Аналогично предыдущему запишем выражение элементарной работы внешних объемных и поверхностных сил:

. (9.61)

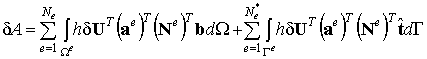
Введем стандартные обозначения элементных векторов сил:

, (9.62)

, (9.63)

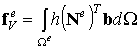
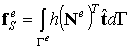
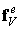
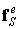
где называется элементным вектором узловых сил, статически эквивалентным заданным объемным силам, называется элементным вектором узловых сил, статически эквивалентным заданным поверхностным силам.

Аналогично предыдущему элементные вектора сил объединяются в глобальные вектора:

, (9.64)

, (9.65)

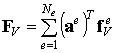
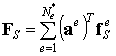
где F_V называется глобальным вектором узловых сил, статически эквивалентным заданным объемным силам, F_S называется глобальным вектором узловых сил, статически эквивалентным заданным поверхностным силам.

Таким образом, формула (9.61) будет представлена в следующем компактном виде:

(9.66)

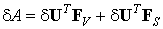
Подставим полученные выражения (9.60) и (9.66) в основную формулу принципа минимума потенциальной энергии Лагранжа (9.37):

(9.66)

. (9.67)

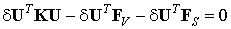
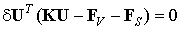
Поскольку вариация глобального вектора узловых перемещений представляет собой вектор, состоящий из независимых произвольных вариаций узловых перемещений, то в общем случае он отличен от нуля. Следовательно, в ноль должно обращаться выражение в круглых скобках. Откуда получаем разрешающую систему конечно-элементных уравнений относительно глобального вектора узловых перемещений:

(9.68)

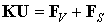
Матричное уравнение (9.68) представляет собой стандартную форму записи системы линейных алгебраических уравнений метода конечных элементов (СЛАУ МКЭ). Особенности формирования входящих в нее матриц и векторов и особенности решения СЛАУ будут рассмотрены в следующих разделах.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Источник

СОДЕРЖАНИЕ

Математическое объяснение

Видно, что энергия находится в экстремуме при равновесии. Аналогичным, но несколько более длинным аргументом можно показать, что

что больше нуля, показывая, что энергия на самом деле минимальна.

Примеры

Рассмотрим, например, знакомый пример мрамора на краю чаши. Если мы рассматриваем мрамор и чашу как изолированную систему, тогда, когда мрамор падает, потенциальная энергия будет преобразована в кинетическую энергию движения мрамора. Силы трения преобразуют эту кинетическую энергию в тепло, и в состоянии равновесия мрамор будет находиться на дне чаши, а мрамор и чаша будут иметь немного более высокую температуру. Общая энергия системы «мраморная чаша» останется неизменной. То, что раньше было потенциальной энергией мрамора, теперь будет заключаться в увеличенной тепловой энергии системы мраморных чаш. Это будет применение принципа максимальной энтропии, изложенного в принципе минимальной потенциальной энергии, поскольку из-за эффектов нагрева энтропия увеличилась до максимально возможного значения при фиксированной энергии системы.

Если, с другой стороны, мрамор опускается на дно чаши очень медленно, так медленно, чтобы не возникало никаких эффектов нагрева (т.е. обратимо), то энтропия мрамора и чаши останется постоянной, а потенциальная энергия мрамор будет передаваться в окружающую среду как энергия. Окружающая среда будет максимизировать свою энтропию с учетом вновь полученной энергии, которая эквивалентна энергии, переданной в виде тепла. Поскольку потенциальная энергия системы теперь минимальна без увеличения энергии из-за тепла мрамора или чаши, общая энергия системы минимальна. Это применение принципа минимума энергии.

Предположим, что x меньше своего равновесного значения. Сила газа, направленная вверх, больше, чем сила груза, направленная вниз, и, если ему дать возможность свободно перемещаться, газ в цилиндре будет быстро толкать гирю вверх, и возникнут силы трения, которые преобразуют энергию в тепло. Если мы укажем, что внешний агент давит на гирю так, чтобы очень медленно (обратимо) позволить весу переместиться вверх до положения равновесия, то тепла не будет, и энтропия системы будет оставаться постоянной, в то время как энергия передан как работа внешнему агенту. Полная энергия системы при любом значении x определяется внутренней энергией газа плюс потенциальная энергия груза:

Поскольку энтропия постоянна, мы можем сказать, что dS = 0 в состоянии равновесия, и по принципу минимума энергии мы можем сказать, что dU = 0 в состоянии равновесия, что дает условие равновесия:

в котором просто говорится, что сила давления газа, направленная вверх ( PA ) на верхнюю поверхность цилиндра, равна силе тяжести, направленной вниз, создаваемой массой ( mg ).

Термодинамические потенциалы

где температура заменила энтропию как естественную переменную. Чтобы понять значение термодинамических потенциалов, необходимо взглянуть на них в ином свете. Фактически их можно рассматривать как (отрицательные) преобразования Лежандра внутренней энергии, в которых некоторые из обширных параметров заменяются производной внутренней энергии по этой переменной (т. Е. Сопряженной с этой переменной). Например, свободная энергия Гельмгольца может быть записана:

и минимум будет, когда переменная T станет равной температуре, поскольку

Свободная энергия Гельмгольца является полезной величиной при изучении термодинамических превращений, при которых температура поддерживается постоянной. Хотя сокращение числа переменных является полезным упрощением, главное преимущество заключается в том, что свободная энергия Гельмгольца минимизирована в состоянии равновесия по отношению к любым неограниченным внутренним переменным для замкнутой системы при постоянной температуре и объеме. Это непосредственно следует из принципа минимума энергии, который гласит, что при постоянной энтропии внутренняя энергия минимизирована. Это можно сформулировать так:

Свободная энергия Гельмгольца в состоянии равновесия будет:

Меняя порядок экстремумов:

показывающий, что свободная энергия Гельмгольца минимизирована в состоянии равновесия.

Источник

В чем состоит принцип минимума потенциальной энергии

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ (уч.10кл. стр.135-142, 153)

Определение потенциальной силы

Работа потенциальной силы

Определение потенциальной энергии

Работа сил трения, тяжести га примере скатывания тела по наклонной плоскости

Принцип минимума потенциальной энергии http://www.skladovka.ru/ холодильники для хранения шуб в москве.

Устойчивое, неустойчивое, безразличное равновесия. Определения и примеры

Работа силы тяжести (уч.10кл.стр.139)

Потенциальная энергия в гравитационном поле. Формула

Работа силы тяжести в гравитационном поле

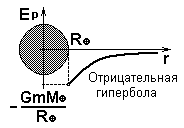
Зависимость потенциальной энергии в поле тяжести от расстояния до центра поля. График

Работа силы упругой деформации

Потенциальная энергия тела при упругом взаимодействии. Формула

Зависимость потенциальной энергии упругой деформации от деформации. График

Упругое и не упругое столкновение. Определения. Переход энергии. (уч.10кл.стр.153)

Закон сохранения полной механической энергии изолированной системы (коротко)

Потенциальная(Консервативная) сила – сила, работа которой при перемещении материальной точки зависит только от начального и конечного положений точки в пространстве.

Работа консервативной силы при перемещении материальной точки по замкнутому контуру равна нулю.

Например, сила тяжести – потенциальная сила, ее работа не зависит от формы траектории (см. выше сила тяжести)

Потенциальной (лат. потенция – возможность) энергией называется энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.

Потенциальная энергия тела в данной точке – скалярная физическая величина, равная работе, совершаемой потенциальной силой при перемещении тела из этой точки в точку, принятую за нуль отсчета потенциальной энергии.

Единица измерения – Дж (Джоуль)

Потенциальной энергией обладает всякое упруго деформированное тело.

Потенциальную энергию сжатого газа используют в тепловых двигателях, пневмоинструменте и т.д.

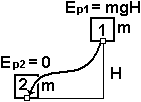
Так работа силы тяжести Ag = Ep1 – Ep2 = mgH

Потенциальная энергия в этом случае характеризует энергию гравитационного притяжения материальной точки к Земле.

Потенциальная энергия материальной точки, поднятой на высоту Н над «нулем»

Потенциальная энергия зависит от координаты (относительно «нуля» потенциальной энергии)

Изменение потенциальной энергии характеризует работу силы тяжести по перемещении тела. Эта работа равна изменению потенциальной энергии, взятому с противоположным знаком. Тело находящееся ниже поверхности земли, имеет отрицательную потенциальную энергию.

В общем случае работа всех сил, действующих на тело равна сумме работ потенциальных и не потенциальных сил: A = Ap + Anp

Принцип минимума потенциальной энергии:

Любая замкнутая система стремиться перейти в такое состояние, в котором ее потенциальная энергия минимальна.

Устойчивое равновесие – равновесие, при котором тело, выведенное из положения равновесия, возвращается в первоначальное положение.

Неустойчивое равновесие – равновесие, при котором тело, выведенное из положения равновесия, не возвращается в первоначальное положение.

Безразличное равновесие – равновесие, при котором соседние положения тела также являются равновесными.

Работа силы тяжести при перемещении тела на высоту Н:

Потенциальная энергия тела массой m в гравитационном поле:

Начало отсчета находится на бесконечно большом расстоянии от Земли (на бесконечности) На этом расстоянии стремиться к нулю и сила гравитационного притяжения к Земле

Расстояние во всех инерциальных системах отсчета одно и тоже. Поэтому потенциальная энергия не зависит от выбора системы отсчета, а зависит от выбора «нуля» отсчета.

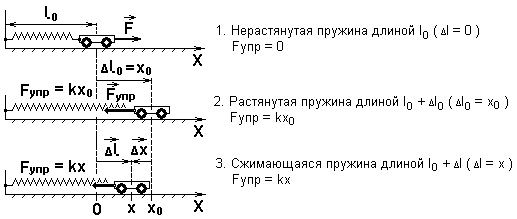
Работа силы упругости при растяжении и сжатии пружины

Потенциальную энергию имеют не только поднятые тела. Рассмотрим работу, совершаемую силой упругости при деформации пружины.

Сила упругости меняется от Fупр = kx0 до Fупр = kx

Средняя сила упругости Fупр.ср = = (x0 + x)

Направление средней силы упругости 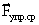и перемещения совпадают

Работа силы упругости зависит только от начального и конечного положений.

Потенциальная энергия пружины (упругодеформированного тела)

x – удлинение или сжатие тела (пружины)

k – жесткость тела (пружины)

Начало отсчета соответствует нерастянутой пружине, удлинение которой x=0

Потенциальная энергия упругодеформированной пружины равна работе силы упругости при переходе пружины из деформированного состояния в недеформированное.

Потенциальная энергия упругодеформированной (сжатой или растянутой) пружины зависит от степени ее деформации.

Важной характеристикой потенциальной энергии является то, что тело не может обладать ею, не взаимодействуя с другими телами.

Потенциальная энергия характеризует взаимодействующие тела, кинетическая – движущиеся. И та, и другая возникают в результате взаимодействия тел.

Если тела взаимодействую между собой только силами тяготения и силами упругости, и никакие внешние силы на них не действуют (или же их равнодействующая равна нулю), то при любых взаимодействиях тел работа сил упругости или сил тяготения равна изменению потенциальной энергии, взятой с противоположным знаком.

В то же время, по теореме о кинетической энергии (изменение кинетической энергии тела равно работе внешних сил) работа тех же сил равна изменению кинетической энергии:

Источник