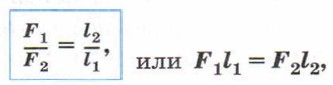в чем состоит правило равновесия рычага 7 класс физика

Правило равновесия рычага

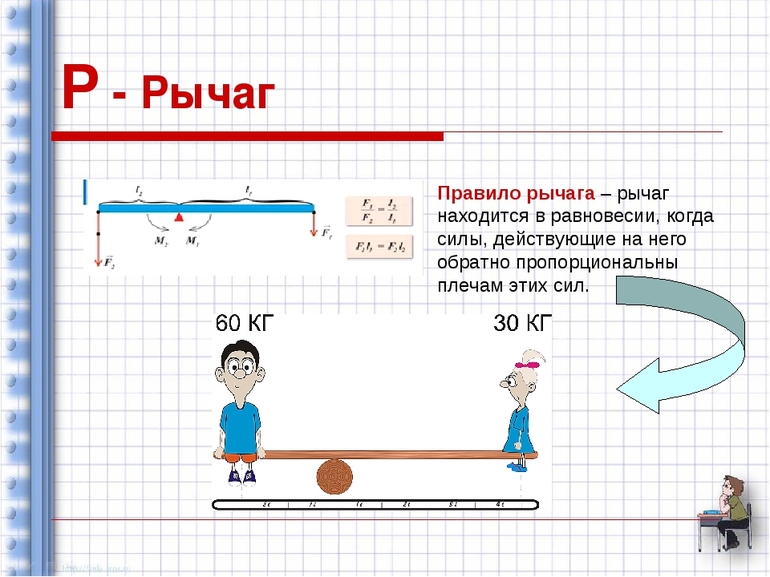
4. На основании подобных опытов более двух тысяч лет назад древнегреческим учёным Архимедом было установлено правило:

рычаг находится в равновесии, если силы, действующие на него, обратно пропорциональны плечам этих сил.

Это правило (условие) равновесия рычага записывают в виде формулы:

где F₁ и F₂ — силы, действующие на рычаг, l₁ и l₂ — плечи этих сил.

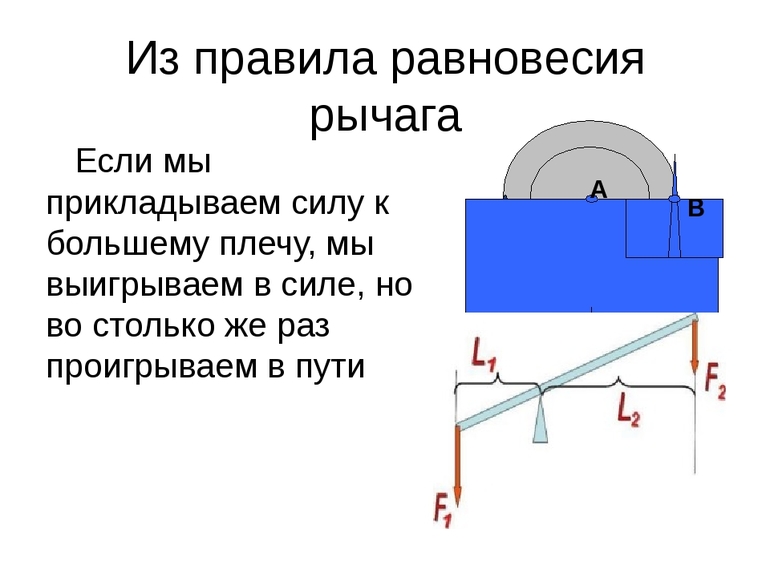
Зная правило равновесия рычага, можно объяснить, как с помощью простого механизма получить выигрыш в силе. Если к длинному концу рычага приложить небольшую силу, то можно уравновесить гораздо большую силу, приложенную к короткому концу рычага.

5. Как можно объяснить выигрыш в силе в примере с тачкой (см. рис. 93), используя правило равновесия рычага?

Силы ₁ и ₂, действующие на тачку, параллельны друг другу и направлены в противоположные стороны. Сила ₂ стремится вращать рычаг по ходу часовой стрелки, а сила ₁ — против её хода.

Плечи сил ₁ и ₂ соответственно равны l₁ и l₂. По правилу равновесия рычага плечо l₂ много меньше плеча l₁, следовательно, чтобы уравновесить рычаг, сила ₁ может быть меньше ₂. Выигрыш в силе очевиден.

6. В основе действия многих машин и механизмов, используемых в быту и технике, лежит правило равновесия рычага. Вы уже знакомы с устройством и принципом действия рычажных весов. Они именно так и называются — «рычажные весы», потому что их основной элемент — рычаг.

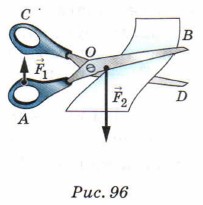
Рассмотрите внимательно обычные ножницы (рис. 96). Они представляют собой пару рычагов, скреплённых в точке О, относительно которой они могут вращаться. Будем считать, что рычаг CD остаётся в покое, а к концу рычага АВ в точке А прикладывается сила ₁ — сила пальцев человека, работающего ножницами. Сила ₂, действующая со стороны рычага на листок бумаги, окажется много больше приложенной силы ₁. На том же принципе основана работа и многих других инструментов: клещей, плоскогубцев, садового секатора и пр.

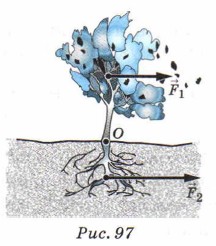
Рычаг встречается повсеместно в живой и неживой природе. Объясняя, например, причину падения деревьев во время урагана, придётся вспомнить о правиле равновесия рычага. Сила сопротивления земли (₂), действующая на корни дерева (рис. 97), может в какой-то момент оказаться недостаточной, чтобы удержать дерево в равновесии, и дерево упадёт под напором порыва ветра (сила ₁).

В организме человека и животного, в теле птиц и насекомых очень много различных рычагов. Только в вашем теле более 200 различных костных рычагов. Очень интересный вывод можно сделать, рассмотрев действие рычага в локтевом суставе человека (рис. 98). В этом рычаге точка опоры (точка О) находится в суставе. Вес груза ₂ приложен к концу рычага, а сила ₁, необходимая для удержания груза, приложена вблизи от точки О. Сила ₁ возникает благодаря сокращению мышц руки человека. В соответствии с правилам равновесия рычага сила ₁ должна быть много больше силы ₂, так как плечо l₁ намного меньше плеча l₂. В данном случае рычаг даёт проигрыш в силе, но выигрыш в расстоянии. Оказывается, сила мышц руки человека гораздо больше веса груза, который он поднимает рукой.

Источник

Рычаг. Равновесие сил на рычаге

Содержание

С древних времен люди используют различные устройства для совершения механической работы. Эти устройства позволяют поднимать груза большой массы или перемещать их. Они называются простыми механизмами.

Например, еще в Древнем Египте (около трех тысяч лет назад) использовали рычаги (рисунок 1). С их помощью передвигали и поднимали на большую высоту огромные каменные плиты.

Рисунок 1. Строительство пирамид по Геродоту (гравюра XVIII века).

В данном уроке мы рассмотрим этот механизм и его устройство. Именно рычаг дает возможность приложить меньшую силу, чем потребовалось бы без него. По этой причине рычаги присутствуют в составе сложных машин и устройств и в современном мире.

Устройство рычага

Рычаг – это любое твердое тело, которое может вращаться вокруг неподвижной опоры.

Взгляните на рисунок 2. В данном случае Образавр использует в качестве рычага обычную палку, чтобы поднять тяжелый камень.

В обоих случаях у этого рычага есть неподвижная точка опоры – точка О. Через нее проходит воображаемая ось, вокруг которой может поворачиваться рычаг.

Сила, с которой Образавр действует на палку (рычаг) меньше веса камня, но, тем не менее, у него получается сдвинуть этот камень. Это говорит о том, что с помощью рычага человек получает выигрыш в силе.

Таким образом, рычаги бывают двух видов (рисунок 3):

Рисунок 3 является схематическим изображением рычагов, показанных на рисунке 2.

Условие равновесия рычага

Рисунок 4. Рычаг.

Рисунок 5. Схематическое изображение рычага.

Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.

Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы. Длина этого перпендикуляра и есть плечо данной силы.

С помощью таких опытов было установлено правило равновесия рычага:

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил

Это правило было установлено Архимедом еще в III веке до н. э. Иногда правило равновесия рычага так и называют – правило Архимеда. Легенда гласит, что после этого открытия Архимед воскликнул: “Дайте мне точку опору, и я переверну Землю!”.

Из правила равновесия следует, что меньшей силой можно уравновесить большую силу при помощи рычага.

Примеры задач

Показать решение и ответ

Решение:

Запишем правило равновесия рычага:

$F_1 = F_2 \cdot \frac = gm \cdot \frac = 9.8 \frac<Н> <кг>\cdot 300 \space кг \cdot \frac<0.6 \space м> <3 \space м>= 2940 \space Н \cdot 0.2 = 588 \space Н$.

СИ:
$0.1 \space кг$
$0.2 \space кг$
$0.5 \space м$
$0.2 \space м$

Показать решение и ответ

$F_2 = P_2 = gm = g(m_1 + m_2) = 9.8 \frac<Н> <кг>\cdot (0.1 \space кг + 0.2 \space кг) = 9.8 \frac<Н> <кг>\cdot 0.3 \space кг \approx 3 \space Н$.

Запишем правило равновесия рычага:

Найдем массу груза:

$m_3 = \frac = \frac<1.2 \space Н><9.8 \frac<Н><кг>> \approx 0.1 \space г = 100 \space г$.

Источник

Характеристика понятия

Описываемое устройство является довольно простым. Но разбираясь в тонкостях правила рычага в физике, стоит отметить наличие у него нескольких составных частей:

Рычаг применяется для преобразования перемещения в силу и наоборот. Таким образом, удаётся добиться перераспределения выполняемой работы в пользу производимого перемещения или прикладываемой силы.

Если рассматривать строение человеческого скелета, можно прийти к выводу, что всем людям с самого рождения предоставляется способность пользоваться системой рычагов. При этом в роли механизма выступают плечи и предплечья.

Начало применения устройства с целью облегчения физической работы датируется древними временами. Имеются сведения, что ещё в Древнем Египте эти приборы шли в ход, когда люди поднимали из реки или колодца наполненный водой сосуд.

В 100 году до нашей эры была издана работа Плутарха под названием «Параллельные жизни». В ней говорится, что Архимеду удалось без посторонней помощи поднять над водой корабль, на борту которого на тот момент находились пассажиры и груз. Для этого были использованы блоки и рычаги. По сей день считается, что именно Архимед изобрёл механизм, поскольку самые древние сохранившиеся письменные работы, свидетельствующие о создании закона, принадлежат перу именно этого философа.

Момент силы

При изучении правила равновесия рычага следует отдельно разобраться в том, что значит единица измерения, называемая моментом силы (или крутящим моментом). Чтобы её изобразить с помощью формулы, необходимо умножить непосредственно величину силы (F) на плечо силы (d).

Схематически это будет изображаться так: М = d x F. Очень важное значение имеет ось вращения. Без её определения действующий момент силы лишён смысла. Использование величины М говорит о способности силы оборачивать систему вокруг оси. Применить её на практике можно на примере гайки, если постараться открутить последнюю без помощи гаечного ключа, а лишь одними руками. Тот же эффект будет наблюдаться и при попытке открыть дверь толчком около петель, а не за ручку.

При решении задач величина М способна приводить к вращению механизм как по ходу часовой стрелки, так и против него. При этом в первом случае момент отрицательный, а во втором — положительный.

Правило рычага

Чтобы разобраться, в чём заключается правило рычага, стоит рассмотреть пример работы классического механизма с двумя плечами и опорой, расположенной далеко от обоих концов доски. Во время применения прибора отмечается действие двух сил на него:

Обычно для создания F прикладываются человеческие усилия, а R определяется массой поднимаемого груза. Механизм достигнет равновесия лишь в том случае, если действующие на него моменты в сумме окажутся равны нулю. С учётом момента силы формулу для правила рычага можно записать так: R х DR — F х DF = 0, где D является плечом силы. F отрицательная из-за того, что стремится оборачивать плечо устройства по кругу в направлении движения часовой стрелки. Если записать формулу в виде равенства, она будет выглядеть так: R х DR = F х DF.

Отсюда следует, что для достижения простым рычагом равновесия достаточно добиться равенства моментов сил действия F и противодействия R. При применении механизма сохраняется энергия системы, свидетельствующая о необходимости проделывания определённой работы во время поднятия груза на какую-либо высоту.

Поскольку для получения значения правила рычага длину плеча умножают на силу, то существует возможность осуществления работы как с применением большей, так и меньшей силы. Но при первом варианте плечо механизма придётся установить на меньшую величину в вертикальном направлении, а второй случай предполагает перемещение плеча на большую величину. Эта особенность называется выигрышем и проигрышем в применении рычага.

Стоит отметить, что значения моментов никак не влияют на работу. Осуществление действия благодаря моменту силы отмечается лишь в тех случаях, когда система начинает поворачиваться на определённый угол по часовой стрелке.

Виды механизмов

Как известно, все рычаги подразделяются на три типа. Основывается эта классификация на относительном расположении опоры к силам R и F. Каждый из видов механизма стоит охарактеризовать отдельно:

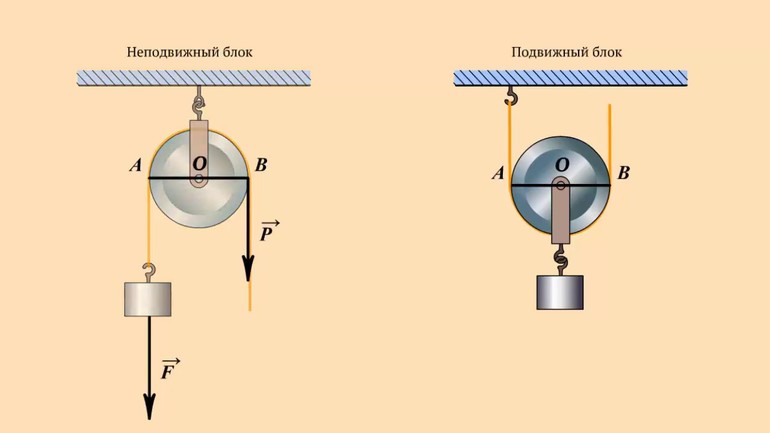
Помимо рычагов, при изучении правила равновесия стоит обратить внимание и на другой простой механизм, называемый блоком. Это цилиндр, оснащённый осью вращения и углублением, сформированным вдоль боковой поверхности. При его применении полностью отсутствует выигрыш в силе и пути, однако, благодаря использованию неподвижного блока, можно поменять направление воздействия F. К устройству применимо правило рычага, но только тогда, когда необходимо добиться выигрыша в силе для подвижных блоков, каждый из которых способен увеличить такое значение вдвое. Но при этом методе идентичная величина проигрывается в пути.

Пример решения задачи

В интернете существует масса приложений со встроенными онлайн-калькуляторами, позволяющими вычислить то или иное значение. Для решения задач по правилу рычага можно воспользоваться этими программами либо же научиться вычислять необходимые величины на основе примеров.

Итак, по условию задачи требуется узнать длину рычага, который позволит 50-килограммовой девушке поднять полуторатонный автомобиль, надавив на механизм всем весом. При этом точка опоры располагается в одном метре от края короткого плеча (D1), где D2 — длинное плечо.

Чтобы выяснить, во сколько раз механизм может дать выигрыш в силе, используется формула F/R=D1/D2. Обе силы оказывают воздействие на рычаг по разные стороны от его опоры, поэтому общая длина доски измеряется по формуле: D = D1+D2.

Согласно условию задачи, величина R, оказывающая действие на плечо D1, это вес автомобиля, обозначаемый Mg. При этом F представляет собой действующую на плечо D2 силу, являющуюся весом девушки (mg). Для получения длины рычага достаточно решить уравнение. Итак, в соответствии с вышеописанной формулой (mg/Mg = D1/D2), чтобы получить D2 необходимо произведение массы авто и длины короткого плеча разделить на вес девушки: (Mg x D1)/mg: D2 = (1500 кг х 1 м)/50 кг = 30 м. Чтобы получить общую длину рычага, понадобится сложить D2 и D1: 30м+1 м. Таким образом, искомая величина будет равна 31 метру.

В наши дни рычаги находят широкое применение как в быту, так и на производстве. Поэтому понимание принципа их работы очень важно практически для каждого человека.

Источник

В чем состоит правило равновесия рычага 7 класс физика

1. Что такое рычаг?

Самый простой и распространенный механизм — рычаг.
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной опоры.

2. Как используют рычаг?

Можно для поднятия груза использовать в качестве рычага лом.
Для этого надо с силой F нажимать на конец лома В или приподнимать конец В.
В любом случае при поднятии груза необходимо преодолеть вес груза Р — силу, направленную вертикально вниз.
Для этого надо повернуть лом вокруг оси, проходящей через неподвижную точку лома — точку его опоры О.

Сила F, с которой человек действует на рычаг, меньше силы Р.
Используя рычаг, получаем выигрыш в силе.

2. Что называют плечом силы?

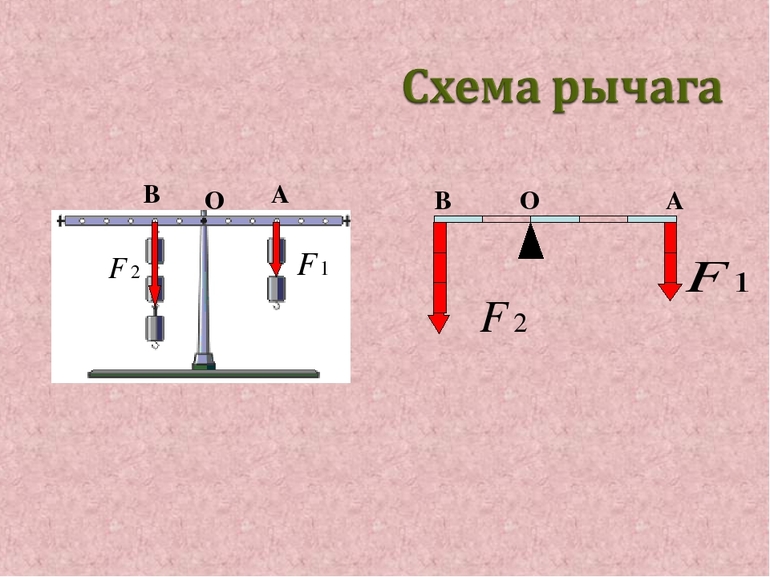
Например, есть рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В.
F1 и F2, действующие на рычаг, направлены в одну сторону.

Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.

3. Как найти плечо силы?

Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
Длина этого перпендикуляра и будет плечом данной силы.

OA — плечо силы F1,
OB — плечо силы F2.

4. Какое действие оказывают на рычаг силы?

Силы, действующие на рычаг, могут повернуть его вокруг оси или по ходу, или против хода часовой стрелки.
На рисунке выше:
С ила F2 вращает рычаг по ходу часовой стрелки.
Сила F1 вращает рычаг против хода часовой стрелки.
Результат действия силы зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу и как направлена.

5. В чем состоит правило (условие) равновесия рычага?

Правило равновесия рычага было установлено Архимедом (287—212 гг. до н. э.).

Правило (условие) равновесия рычага:
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.

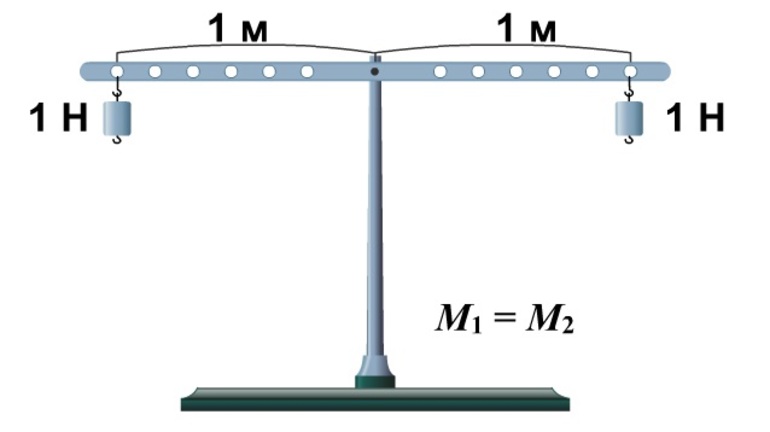
К рычагу по обе стороны от точки опоры подвешивают грузы так, чтобы рычаг оставался в равновесии.
Действующие на рычаг силы равны весам этих грузов.
Далее измеряют модули сил и их плечи.
Если сила F2 уравновешивает силу F1, то плечо меньшей силы в 2 раза больше плеча большей силы.

где
F1 и F2 — силы, действующие на рычаг,
l1 и l2 — плечи этих сил.

6. Как уравновесить меньшей силой большую?

При помощи рычага можно меньшей силой уравновесить большую силу.
При этом плечо меньшей силы должно быть длиннее плеча большей силы.

Задача.
Человеку необходимо поднять с помощью рычага плиту массой 240 кг.
Большее плечо рычага равно 2,4 м.
Меньшее плечо рычага равно 0,6 м.
Какую силу надо приложить человеку к большему плечу рычага?

Человек преодолевает силу 2400 Н, прикладывая свою силу, равную 600 Н.
Здесь рычаг дает выигрыш в силе в 4 раза.
Однако плечо, на которое действует человек, в 4 раза длиннее того, на которое действует вес плиты:
2,4 м : 0,6 м = 4.

Источник

Урок физики по теме «Простые механизмы. Рычаг»

Презентация к уроку

Цель урока: изучить самый простой и распространенный простой механизм – рычаг.

Оборудование: компьютер, проектор, презентация PowerPoint, рычаг-линейка, набор грузов, ножницы, рычажные весы, неподвижный блок, карточки-задания.

I. Актуализация опорных знаний

Повторение изученного материала. Учащимся предлагается выполнить тест по теме: «Механическая работа. Мощность». [3]

II. Изучение нового материала

Демонстрация: ножницы, рычажные весы, неподвижный блок, рычаг-линейка.
Подведение к изучению новой темы. Учащимся задается проблемный вопрос: Что объединяет эти устройства и приспособления? (Выслушиваются мнения учащихся). Попробуем выяснить это.

1. Простые механизмы(слайд 1)

Физические возможности человека ограничены, поэтому с давних времен он использовал устройства, которые были способны преобразовывать силу человека в значительно большую силу. Такие устройства – простые механизмы использовали еще 3 тыс. лет назад при строительстве пирамид в Др.Египте (слайд 2).

Записываем тему урока.

Простые механизмы – приспособления, служащие для преобразования силы.
Виды простых механизмов: рычаг (блок, ворот); наклонная плоскость (клин, винт)
Назначение – получить выигрыш в силе (слайд 3).

– Сегодня мы познакомимся с одним из видов простых механизмов – рычагом.

Цель: выяснить, что представляет собой рычаг, каково его устройство и назначение (слайд 4).
Из жизненного опыта мы знаем, что человеку трудно поднять тяжелый предмет. Сила, которую он прикладывает, порой, недостаточна, чтобы преодолеть силу тяжести предмета. В этом может помочь нехитрое приспособление, например лом, или рычаг.

Рычаг – твердое тело, которое может вращаться вокруг неподвижной опоры.

Рассмотрим устройство рычага. Изобразим его графически и перечислим основные части (слайд 5):

Существует два вида рычагов: рычаг 1 рода, рычаг 2 рода (слайд 6).
Учащимся демонстрируются рисунки рычагов и задается проблемный вопрос: В чем разница между этими видами рычагов?
У рычагов первого рода неподвижная точка опоры располагается между линиями действия приложенных сил. У рычагов второго рода неподвижная точка опоры располагается по одну сторону линий действия приложенных сил.

Назначение рычага – получить выигрыш в силе.

3. Условие равновесия рычага

Демонстрационный опыт: с помощью рычага уравновесить силу 6Н силой 3Н. (вызывается ученик). Вывод: рычаг позволил получить выигрыш в силе в 2 раза.
В 3 веке до н.э. Архимед открыл правило, по которому находят выигрыш в силе. Сейчас мы установим это правило.

Будем уравновешивать рычаг, результаты измерений занесем в таблицу:

l₁162263326234223626211

Учащиеся заполняют таблицу и выполняют расчеты: F₂/F₁, l₁/ l₂. Затем анализируем полученные результаты по последним колонкам таблицы. Формулируем вывод проведенного эксперимента (слайд 7) и записываем правило [1, стр. 139]:

Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил:

Из этого правила следует, что с помощью рычага меньшей силой можно уравновесить большую силу.

4. Применение рычагов

Рычаги нашли широкое применение в быту и технике. Правило равновесия рычага лежит в основе действия различных инструментов и устройств (слайд 8).
Я надеюсь, что теперь вы точно сможете ответить на вопрос, позвучавший в начале урока!

При равновесии рычага на его меньшее плечо действует сила 300 Н, на большее – 20 Н. Длина меньшего плеча 5 см. Определите длину большего плеча (слайд 14).

IV. Домашнее задание (слайд 15)

Перышкин А.В. Физика. 7 класс: §55, 56, Упр. 30 (1)

V. Рефлексия

Список литературы:

1) Перышкин А.В. Физика. 7 класс
2) Лукашик В.И. Сборник задач по физике. 7-9 классы.
3) Марон А.Е. Физика. 7 класс: учебно-методическое пособие.

Источник