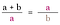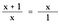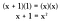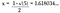в чем смысл золотого сечения
Божественная гармония: что такое золотое сечение простыми словами. Тайны мироздания в числах
Эта гармония поражает своими масштабами.
Вы что-нибудь слышали о Божественной гармонии или Золотом сечении? Задумывались ли о том, почему нам что-то кажется идеальным и красивым, а что-то отталкивает?
Если нет, то вы удачно попали на эту статью, потому что в ней мы обсудим золотое сечение, узнаем что это такое, как оно выглядит в природе и в человеке. Поговорим о его принципах, узнаем что такое ряд Фибоначчи и многое многое другое, включая понятие золотой прямоугольник и золотая спираль.
Да, в статье много изображений, формул, как-никак, золотое сечение — это еще и математика. Но все описано достаточно простым языком, наглядно. А еще, в конце статьи, вы узнаете, почему все так любят котиков =)
Что такое золотое сечение?
Если по-простому, то золотое сечение — это определенное правило пропорции, которое создает гармонию?. То есть, если мы не нарушаем правила этих пропорций, то у нас получается очень гармоничная композиция.
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому.
Но, кроме этого, золотое сечение — это математика: у него есть конкретная формула и конкретное число. Многие математики, вообще, считают его формулой божественной гармонии, и называют «асимметричной симметрией».
До наших современников золотое сечение дошло со времен Древней Греции, однако, бытует мнение, что сами греки уже подсмотрели золотое сечение у египтян. Потому что многие произведения искусства Древнего Египта четко построены по канонам этой пропорции.
Золотое сечение в математике
Считается, что первым ввел понятие золотого сечения Пифагор. До наших дней дошли труды Евклида (он при помощи золотого сечения строил правильные пятиугольники, именно поэтому такой пятиугольник назван «золотым»), а число золотого сечения названо в честь древнегреческого архитектора Фидия. То есть, это у нас число «фи» (обозначается греческой буквой φ), и равно оно 1.6180339887498948482… Естественно, это значение округляют: φ = 1,618 или φ = 1,62, а в процентном соотношении золотое сечение выглядит, как 62% и 38%.
В чем же уникальность этой пропорции (а она, поверьте, есть)? Давайте для начала попробуем разобраться на примере отрезка. Итак, берем отрезок и делим его на неравные части таким образом, чтобы его меньшая часть относилась к большей, как большая ко всему целому. Понимаю, не очень пока ясно, что к чему, попробую проиллюстрировать наглядней на примере отрезков:
Итак, берем отрезок и делим его на два других, таким образом, чтобы меньший отрезок а, относился к большему отрезку b, так же, как и отрезок b относится к целому, то есть ко всей линии (a + b). Математически это выглядит так:
Этот правило работает бесконечно, вы можете делить отрезки сколь угодно долго. И, видите, как это просто. Главное один раз понять и все.
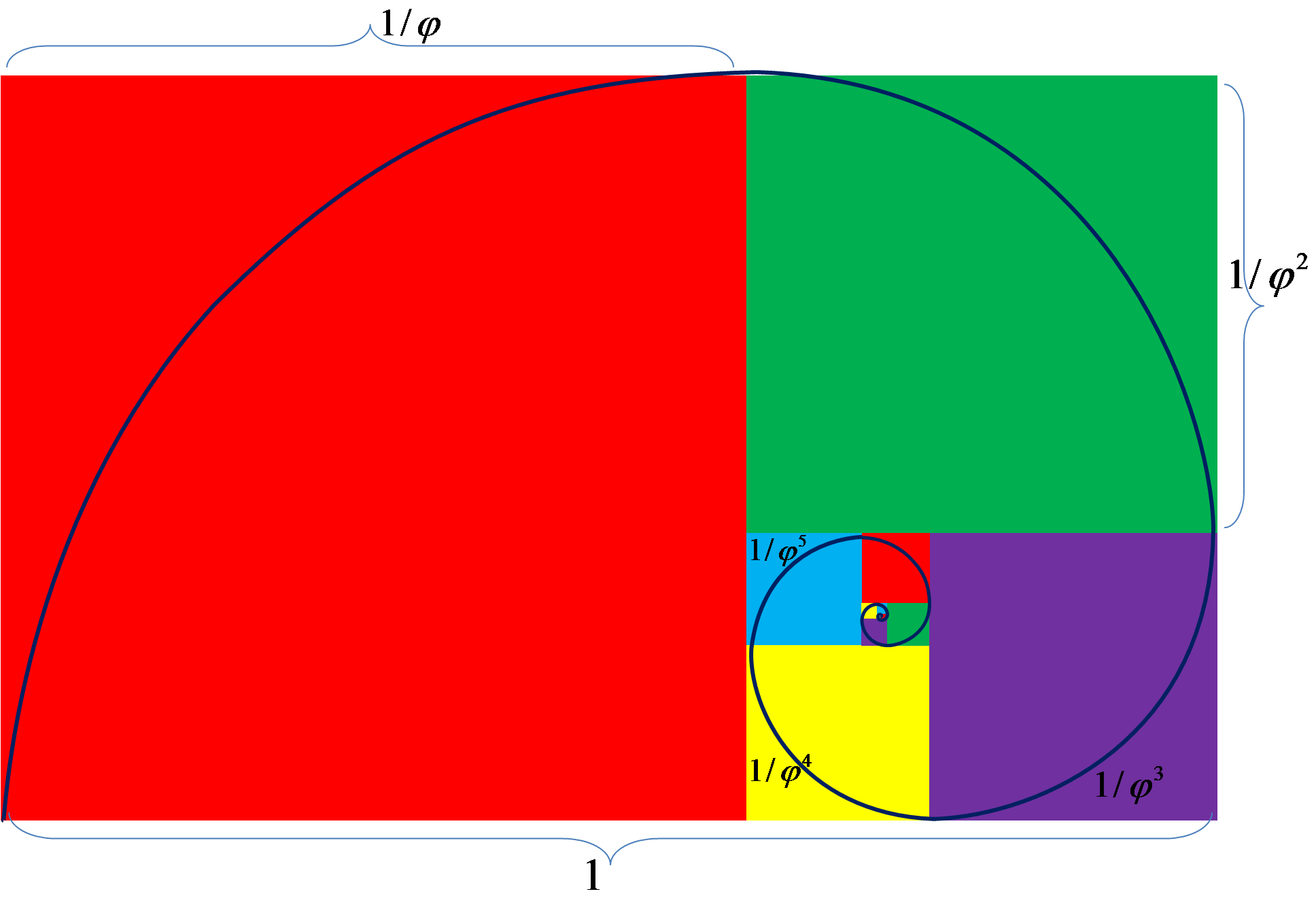
Но теперь рассмотрим более сложный пример, который попадается очень часто, так как золотое сечение еще представляют в виде золотого прямоугольника (соотношение сторон которого равно φ = 1,62). Это очень интересный прямоугольник: если от него «отрезать» квадрат, то мы снова получим золотой прямоугольник. И так бесконечно много раз. Смотрите:
Но математика не была бы математикой, если бы в ней не было формул. Так что, друзья, сейчас будет немножко «больно». Решение золотой пропорции спрятала под спойлер, очень много формул, но без них не хочу оставлять статью.
Что такое «золотое сечение»?
На протяжении веков «золотое сечение» считается самым прекрасным соотношением в искусстве и архитектуре.
«Золотое сечение», называемое также «золотая пропорция» или «золотое соотношение», было обнаружено во многих самых знаменитых творениях человечества — от древнегреческого Парфенона до творений Сальвадора Дали. Возможно, вы уже читали на эту тему статью «Нереализованное влияние золотого сечения».
Не важно, считаете ли вы, что эта божественная пропорция является поистине знамением красоты или просто предвзятым выбором, но, без сомнения, это одно из самых интригующих чисел в мире. Поэтому, сейчас мы поговорим о математической основе «золотого сечения».
Впервые о «золотом сечении» упоминает древнегреческий математик Евклид около 300 лет до нашей эры. В шестой книге своего трактата «Начала» Евклид дает определение «золотого сечения». Он поручает нам взять отрезок линии и разделить его на два меньших сегмента так, что отношение всей линии (a + b) к отрезку a будет таким же, как отношение отрезка a к сегменту b:
Что эквивалентно пропорции:
Евклид использовал «золотое сечение» для построения правильного пятиугольника. Отношение диагонали правильного пятиугольника к его стороне равно золотому сечению. Правильный пятиугольник (пентагон) еще называют «золотой пятиугольник».
Золотой прямоугольник
«Золотое сечение» часто представляют как «Золотой прямоугольник» — прямоугольник с отношением длин сторон примерно 1,618:1.
Этот прямоугольник обладает тем свойством, что если от него отрезать квадрат, то снова получится золотой прямоугольник меньшего размера и так до бесконечности.
На самом деле, соотношение сторон «золотого прямоугольника» — это иррациональное значение 1,618034…, т.е. бесконечная десятичная дробь, не имеющая периода.
Это число и есть пропорция «золотого сечения», оно обозначается греческой буквой Фи в честь древнегреческого скульптора и архитектора Фидия, мастера, воплотившего его в своих работах.
Решение «золотой пропорции»
Чтобы найти значение 1,618034…, мы должны решить пропорцию, показанную выше. Для простоты предположим, что b = 1 и a = x и найдем решение для x.
Шаг 1. Сделаем перекрестное умножение:
Шаг 2. Приведем уравнение к 0:
Шаг 3. Решим квадратное уравнение:
Поскольку мы работаем с длинами, нам нужно только положительное решение:
Решение найдено! «Золотое сечение» выражается, как дробь.
Для проверки подставим a = 1.618 и b = 1, чтобы убедиться, что наша пропорция верная:
Обратите внимание, как интересно: мы можем написать «золотое соотношение» при помощи самого себя. Это потрясающе!
Золотое сечение: почему оно везде и что о нем нужно знать
Золотое сечение – это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве – во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.
Определение
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая ко всему целому. Приблизительная его величина – 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.
Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом отражающим структуру и порядок нашего мироустройства.
История
Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой – Отца, а целое – Святой дух.
Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.
Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.
Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.
Природа
Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.
Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.
Человек
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек – это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.
В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века.
Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.
В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела – 8:5.
Искусство пространственных форм
Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика». Долгое время художники следователи этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.
Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна будь-то камин, этажерка, кресло или сам поэт строго вписаны в золотые пропорции.
Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.
И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.
Слово, звук и кинолента
Формы временно̀го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи – 5, 8, 13, 21, 34.
Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого сечения.
Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.
Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух – в Одессе. Переход на сцены в городе и есть золотая середина фильма.
Золотое сечение. Божественная пропорция
Числовая величина золотого сечения – 1, 6180339887 (и это еще округление =)) до десятого знака!)
Пример золотого сечения в лучах пятиконечной звезды.
С Вашего позволения, я опущу многострочные математические фомулы и фомулировки =) Перейдем сразу к Прекрасному!
Зачатки этого понятия встречаются еще в античной литературе, датированной 300 гг. до нашей эры, а «божественная пропорция» широко применялась в трудах и работах мастеров Эпохи Возрождения. Иоган Кеплер, астроном 16 в. назвал золотое сечение одним из сокровищ геометрии. Он впервые обращает внимание то, как проявляется ЗС в ботанике (рост растений и строение стеблей и соцветий).
В середине 19 в. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение лежит в основе некой среднестатистической пропорции человеческого тела. Деление тела точкой пупка – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 к 8 = 1,625 и несколько ближе подходят к ЗС, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 к 5 = 1,6. Пропорции золотого сечения проявляются и в отношении всех частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.
На протяжении веков существовало общеприянтое мнение, что рукотворные объекты, созданные с применением принципа ЗС, воспринимаются Человеком как наиболее гармоничные, совершенные. Пропорции золотого сечения можно выделить в проекциях египетских пирамид. Соотношение сторон плана Парфенона в Афинском Акрополе также являет собой не простое кратное число, а бесконечно дробное (догадайтесь, какое?). Таковыми же являются соотношение сторон планов и фасадов многих византийских церквей, романских готических соборов. Принято считать, что еще со времен Ренессанса многие художники и архитекторы сознательно используют принципы золотого сечения в своих творениях.
Золотое сечение на примере фасада храма Парфенона
Однако же, бытует и мнение, что значение ЗС в искусстве сильно преувеличенно, порой притянуто за уши исследователями, либо основано наошибочных расчетах. Тут каждый останется при своем. Помню, как на втором курсе в архитектурном нас, лопоухих, профессора пытались приобщить к прекрасному и долго-долго втолковывали про принципы золотого сечения в зодчестве, ряды Фибоначчи и прочее-прочее =)) Но настоящее понимание этой волшебной геометрии пришло ко мне много позже, при изучении бионики (один из стилей архитектуры), которая базируется именно на совершенстве природных форм. Согласитесь, мы не в силах оспаривать очевидное, а примеры идеальной пропорции встречаются сплошь и рядом: в раковинах аммонитов, в расположении ветвей на стебле растения, прожилках листьев. Ведь все, что приобретало какую-то форму, образовывалось, росло, осуществляло свое развитие в основном в двух вариантах – рост вверх или расстилание по поверхности земли и закручивание по спирали. Раковина закручена по спирали. И вообще, представление о золотом сечении будет неполным, если не сказать о спирали. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали: увеличение ее шага всегда равномерно.
Полюбуйтесь, как наглябно иллюстрирует природа принципы Золотого сечения! Совершенные спирали без изъян, соотношения витков которых строго соответсвует канонам и принципам построения ЗС.
«Золотое сечение» в экономике – что это?
Несколько слов о «золотом сечении» в традиционном смысле
Считается, что если отрезок разделить на части таким образом, что меньшая его часть будет относиться к большей, как бОльшая – к целому отрезку, то такое разделение дает пропорцию 1/1,618, которую древние греки, позаимствовав ее у еще более древних египтян, назвали «золотым сечением». И что многие архитектурные сооружения – соотношения контуров строений, соотношение между их ключевыми элементами — начиная с египетских пирамид и кончая теоретическими построениями Ле Корбюзье — основывались на этой пропорции.
Ей же соответствуют числа Фибоначчи, спираль которого дает развернутую геометрическую иллюстрацию этой пропорции.
Более того, размеры человеческого тела (от подошв до пупка, от пупка до головы, от головы до пальцев поднятой руки), начиная от идеальных пропорций, увиденных в Средневековье (витрувианский человек и проч.), и кончая антропометрическими измерения населения СССР, довольно-таки близки к этой пропорции.
А если добавить, что подобные фигуры обнаружены в совершенно разнородных биологических объектах: раковинах моллюсков, расположении семян в подсолнухе и в кедровых шишках, то понятно почему иррациональное число, начинающееся как 1,618 объявлялось «божественным» — его следы прослеживаются даже в форме галактик, тяготеющих к спирали Фибоначчи!
С учетом всех перечисленных примеров, можно предполагать:
В экономике
Широко известны и интенсивно используется диаграммы Лоренца для визуализации доходов населения. Эти мощный макроэкономический инструмент с разнообразными вариациями и уточнениями (децильный коэффициент, индекс Джини) используются в статистике для социально-экономического сопоставления стран и их особенностей и могут быть обоснованием для принятия больших политических и бюджетных решений в области налогообложения, здравоохранения, выработки планов развития стран и регионов.
И хотя в нормальном бытовом сознании доходы и расходы связаны между собой накрепко, в Гугле это не так… Поразительно, но найти связь диаграмм Лоренца с распределением расходов мне удалось только у двух российских авторов (буду признателен, если кто-то знает подобные работы как в русском, так и англоязычном секторе интернета).
Первая — диссертация Т. М. Буевой. Диссертация была посвящена, в частности, оптимизации расходов на марийских птицефабриках.
Другой автор, В.В. Матохин (взаимные ссылки авторов имеются), подходит к делу более масштабно. Матохин, физик по исходному образованию, занимается статистической обработкой данных, используемых при принятии управленческих решений, а также оценкой адаптивности и управляемости компаний.
Концепция и примеры, приводимые ниже, почерпнуты из работ В. Матохина и его коллег (Матохин, 1995), (Antoniou и др., 2002), (Крянев, и др., 1998), (Матохин и др. 2018). В связи с этим следует добавить, что возможные ошибки в интерпретации их работ являются исключительной собственностью автора этих строк и не могут быть приписаны исходным академическим текстам.
Неожиданное постоянство
Отраженное на ниже представленных графиках.
1. Распределение грантов по конкурсу научно-технических работ по Государственной программе “Высокотемпературная сверхпроводимость”. (Матохин, 1995)

Рис.1. Пропорции в ежегодном распределении средств по проектам в 1988-1994 гг..
Основные характеристики ежегодных распределений приведены в Табл.3, где SN — ежегодная сумма распределяемых средств (в млн. руб.), а N — число финансируемых проектов. С учетом того, что за эти годы менялся персональный состав жюри конкурса, бюджет конкурса и даже масштаб денег (до реформы 1991-го года и после), стабильность реальных кривых во времени поразительна. Черная полоса на графике составлена из экспериментальных точек.
| 1988 | 1989 | 1990 | 1991 | 1992 | 1993 | 1994 | ||
| S | 273 | 362 | 432 | 553 | 345 | 353 | 253 | X |
| Sn | 143.1 | 137.6 | 136.9 | 411.2 | 109.4 | 920 | 977 | Y |
2. Кривая расходов, связанных с продажами товарных запасов (Котляр, 1989) 
Рис.2
3. Тарифная сетка жалований чинам
В качестве примера для построения диаграммы взяты данные из документа «Ведомость: сколько каким чинам по штатам обыкновенного годового жалования в год иметь положено» (Суворов, 2014)(«Наука побеждать»).
| Чин | Жалование (руб.) |
| Полковник | 585 |
| Подполковник | 351 |
| Майор Пример | 292 |
| Майор Секунд | 243 |
| Квартермистр | 117 |
| Адъютант | 117 |
| Комиссар | 98 |
| . | . |

Рис. 3. Диаграмма соразмерности годовых жалований по чинам
4. Осредненный рабочий график американского менеджера среднего звена (Mintzberg, 1973) 
Рис.4
Приведенные нормированные графики позволяют предполагать, что в иллюстрируемых ими хозяйственных активностях имеется общая закономерность. При радикальном различии по конкретике хозяйственной деятельности, по ее месту и времени, весьма вероятно, что сходство графиков продиктовано неким фундаментальным условием функционирования экономических систем. Не иначе, как за тысячелетия ведения хозяйственной деятельности на основании огромного числа проб и ошибок субъекты этой деятельности нащупали некоторую оптимальную стратегию распределения ресурсов. И интуитивно используют ее в текущей деятельности. Такое предположение хорошо согласуется с известным принципом Парето: 20% наших усилий дают 80% результатов. Здесь явно наблюдается нечто подобное. Приведенные графики выражают эмпирическую закономерность, которая в случае преобразования в диаграмму Лоренца с достаточной точностью описывается при показателе степени «альфа» равном 2. При этом показателе диаграмма Лоренца превращается в часть окружности.
Можно назвать эту, еще не имеющую устойчивого наименования характеристику, выживаемостью. По аналогии с выживаемостью в дикой природе, выживаемость хозяйственной системы определяется ее наработанным приспособлением к условиям социально-экономической среды и способностью адаптироваться к изменениям рыночных условий.
Это значит, что система, в которой распределение расходов близко к идеальному (при показателе степени «альфа», равном 2, или распределением расходов «по окружности»), имеет наибольшие шансы сохраниться в существующем виде. Примечательно, что в ряде случаев такое распределение определяет и наибольшую рентабельность предприятия. Например, здесь. Чем меньше коэффициент отклонения от идеального, тем выше рентабельность предприятия (Буева, 2002).
| Наименование хозяйства, района | Рентабель-ность (%) | Коэффициент отклонения | |
| 1 | ГУП п/ф «Волжская» Волжского р-она | 13,0 | 0,336 |
| 2 | СПК п/ф «Горномарийская» | 11,1 | 0,18 |
| 3 | УМСП с-з «Звениговский» | 33,7 | 0,068 |
| 4 | ЗАО «Марийское» Медведевского р-на | 7,5 | 0,195 |
| 5 | ОАО «Тепличное» Медведевского р-на | 16,3 | 0,107 |
| . | |||
| 47 | СПК (к-з) «Рассвет» Советского р-она | 3,2 | 0,303 |
| 48 | С-з «Броневик» Килемарского р-она | 14,2 | 0,117 |
| 49 | СПК СХА «Авангард» Моркинского р-она | 6,5 | 0,261 |
| 50 | СХА к-з им. Петрова Моркинского р-она | 22,5 | 0,135 |
Практические выводы
Планируя расходы, как компании, так и домохозяйства, полезно построить по ним кривую Лоренца и сверить ее с идеальной. Чем ближе ваша диаграмма будет к идеальной, тем вероятнее, что планируете правильно и что ваша деятельность будет успешна. Такая близость подтверждает, что ваши планы близки к опыту хозяйственной деятельности человечества, отложившемся в таких общепризнанным эмпирических закономерностях, как принцип Парето.
Однако можно предположить, что здесь речь идет о функционировании зрелой хозяйственной системы, ориентированной на рентабельность. Если же речь не идет о максимизации прибыли, а, например, о задаче модернизации компании или о принципиальном увеличении ее доли рынка, ваша кривая распределения расходов будет отходить от окружности.
Понятно, что и в случае старт-апа с его специфической экономикой диаграмма Лоренца, отвечающая наибольшей вероятности успеха, будет также отклоняться от окружности. Можно высказать гипотезу, что отклонения кривой распределения расходов внутрь окружности соответствует как повышенным рискам, так и пониженной адаптивности компании. Однако без опоры на большие статистические массивы по старт-апам (как успешным, так и неуспешным) обоснованные квалифицированные прогнозы вряд ли возможны.
По другой гипотезе, отклонение кривой распределения расходов от окружности наружу, может быть сигналом как чрезмерной зарегулированности управления, так и сигналом надвигающегося банкротства. Для проверки этой гипотезы так же необходима определенная эталонная база, которая, как и в случае старт-апов, вряд ли существует в открытом доступе.