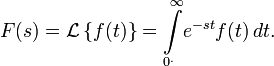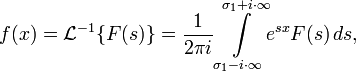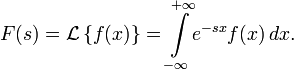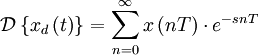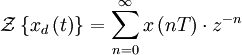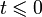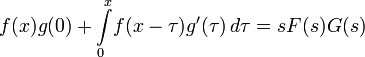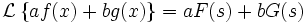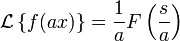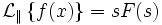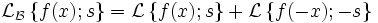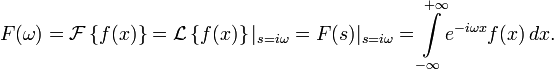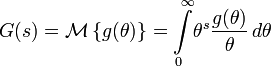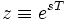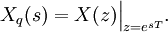в чем смысл преобразования лапласа
Преобразование Лапласа
По этой ссылке вы найдёте полный курс лекций по математике:
рассмотрели интегральное преобразование Фурье с ядром K(t, О = е Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t, Преобразование Лапласа позволяет освободиться от этого ограничения. Определение 1. Функцией-оригиналом будем называтьвсякую комплекснозначную функцию f(t) действитсл ьного аргумента t, удовлетворя юшую следующим условиям:
1. f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем накаждом конечном интервалеоси *такихточек можетбыть лишь конечное число; 2. функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при 3. при возрастании t модуль f(t) возрастает не быстрее показательной функции, т. е. существуют числа М > 0 и s такие, что для всех t Ясно, что если неравенство (1) выполняется при некотором s = aj, то оно будет ВЫПОЛНЯТЬСЯ и при ВСЯКОМ 82 > 8].
Точная нижняя грань s0 всех чисел з, «о = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t). Замечание. В общем случае неравенство не имеет места, но справедлива оценка где е > 0 — любое. Так, функция имеет показатель роста в0 = Для нее неравенство \t\ ^ М V* ^ 0 не выполняется, но верно неравенство |f| ^ Меи. Условие (1) гораздо менее ограничительное, чем условие (*). Пример 1. функция не удовлетворяет условию (»), но условие (1) выполнено при любом s ^ I и А/ ^ I; показатель роста 5о = • •
Так что является функцией-оригиналом. С другой стороны, функция не является функцией-оригиналом: она имеет бесконечный порядок роста, «о = +оо. Простейшей функцией-оригиналом является так называемая единичная функция Если некоторая функция удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение уже является функцией-оригиналом.
Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции /(/); ядро преобразования K(t> р) = e
pt. Тот факт, что функция имеет своим изображением F(p), будем записывать Пример 2. Найти изображение единичной функции r)(t).
Возможно вам будут полезны данные страницы:
Функция является функцией-оригиналом с показателем роста в0 — 0. В силу формулы (2) изображением функции rj(t) будет функция Если то при интеграл в правой части последнего равенства будет сходящимся, и мы получим так что изображением функции rj(t) будет функция £. Как мы условились, будем писать, что rj(t) = 1, и тогда полученный результат запишется так: Теорема 1. Лгя всякой функции-оригинала f(t) с показателем роста з0 изображение F(p) определено в полуплоскости R ер = s > s0 и является в этой полуплоскости аналитической функцией (рис. 3).
Пусть Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при a > Используя (3), получаем что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Дифференцируя выражение (2) формально под знаком интеграла по р, находим Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).
Если тонка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то Пример 3. Найдем еще изображение функции любое комплексное число. Показатель росга «о функции /(() равен а. 4 Считая Rep = я > а, получим Таким образом, При а = 0 вновь получаем формулу Обратим внимание на то, что изображение функции eat является аналитической функцией ар1умента р не только в полуплоскости Rep > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс.
В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Rep > «о функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Rep = so, или на самой этой прямой. Замечай не. В операционном исчислении иногда пользуются изображением функции /(f) по Хевисайду, определяемым равенством и отличающимся от мображения по Лапласу множителем р. §2.
Теорема 12. Если аналитическая в полуплоскости so функция F(p) 1) стремится к нулю при в любой полуплоскости R s0 равномерно относительно arg р; 2) интеграл сходится абсолютно, то F(p) является изображением некоторой функции-оригинала Задача. Может ли функция F(p) = служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению. 3.1. Отыскание оригинала с помощью таблиц изображений Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду.
Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа. Пример 1. Найти оригинал для Запишем функцию F Использование теоремы обращения и следствий из нее Теорема 13 (обращения). Если функция fit) есть функция-оригинал с показателем роста s0 и F(p) — ее изображение, то в любой точке непрерывности функции f(t) выполняется соотношение где интеграл берется вдоль любой прямой и понимается в смысле главного значения, т. е. как Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина. В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а) функция-оригинал-с показателем роста s0. Рассмотрим функцию любое. Функция удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье, Подставляя в (3) выражение найдем где F(p) — преобразование Лапласа функции f(t) при р = 8 + Формулу (2) можно переписать в виде откуда получаем формулу обращения преобразования Лапласа Как следствие из теоремы обращения получаем теорему единственности. Если число 5, фигурирующее в формуле (1), взять большим всех то по формуле обращения, которая в этих условиях применима, получим Рассмотрим замкнутый контур Гд (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = з), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри Гл. По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь Второе слагаемое слева в равенстве (5) стремится к нулю при R оо. если в ней заменить р на iz и учесть, что F(p) 0 при Rep +оо. Переходя в равенстве (5) к пределу при R-* оо, мы получим слева а справа,— сумму вычетов по всем полюсам функции F(p) ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Основные определения Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений Замечание. Перейдем в уравнении (1) от оригиналов к изображениям. Имеем Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) — Оригинал для Х(р) будет искомым решением x(t) задачи (1)-(2). Обший случай линейного дифференциального уравнения n-го порядка (n ^ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается. Приведем общую схему решения задачи Коши Х(р) = Задача Коши в пространстве оригиналов IV I Решение задачи Коши Т-Г’ Операторное уравнение в пространстве изображений Решение операторного уравнения III II Здесь Л означает применение к 1 преобразование Лапласа, JT1 — применение к III обратного преобразования Лапласа. Пример 1. Решить задачу Коши I. Операторное уравнение откуда По теореме о дифференцировании изображения Поэтому Формула Дюамеля В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля. Если известно решение Х\ (t) дифференциального уравнения с той же левой частью и правой частью, равной единице, при нулевых начальных условиях то формула Дюамеля (4) позволяет сразу получить решение исходной задачи В самом деле, операторные уравнения, отвечающие задачам ), имеют соответственно вид и где F(p) — изображение функции ) легко находим Отсюда по формуле Дюамеля t или, поскольку Пример 2. Решить задачу Коши Рассмотрим вспомогательную задачу Применяя операционный метод, находим По формуле (П) получаем решение x(t) исходной задачи: ПРЕОБРАЗОВАНИЕ ЛАПЛАСА Основные определения Свойства Свертка функций Теорема умножения Отыскание оригинала по изображению Использование теоремы обращения операционного исчисления Формула Дюамеля Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Решение интегральных уравнений 4.2. Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы. Оригинал для него будет решением исходной системы дифференциальных уравнений. Пример 3. Найти решение линейной системы удовлетворяющее начальным условиям 4 Пусть Пользуясь свойством линейности преобразования Лапласа и теоремой о дифференцировании оригиналов, сводим исходную задачу Коши к операторной системе Решение исходной задачи Коши 4.3. Решение интегральных уравнений Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла. Пример 4. Решить интегральное уравнение 4 Применяя преобразование Лапласа к обеим частям (14), получим Функция является решением уравнения (14) (подстановка уравнение (14) обращает поело дне© в тождество Замечание. Преобразование Лапласа может быть использовано также при решении некоторьж задач для уравнений математической физики. Функция-оригинал Преобразование Лапласа Упражнения Установите, каше из указанных функций являются функциями-оригиналами: Пользуясь свойствами преобразования Лапласа, найдите изображения следующих функций: Найдите изображение следующих функций, заданных графически: Найдите оригиналы по заданному изображению: Решите задачу Коши для следующих дифференциальных уравнений: Решите задачу Коши доя следующих систем дифференциальных уравнений: Решите интегральные уравнения: Присылайте задания в любое время дня и ночи в ➔ Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института. Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды. Исследование функции изображения часто дает гораздо лучшее физическое понимание поведения линейных систем по сравнению с исследованиями во временной области. Прежде всего, резонансное поведение физических систем легче описать в частотной области. Из-за лучшей сходимости по сравнению, например, с преобразованием Фурье, передаточные функции все еще можно анализировать, даже если линейная система нестабильна. Первые упоминания об идее преобразования Лапласа уже можно найти в работе базельского математика и физика Леонарда Эйлера (1707–1783, Institutiones Calculi Integratedis, vol. 2, 1768). Преобразование Лапласа названо в честь французского математика и астронома Пьера-Симона Лапласа (1749–1827), который ввел преобразование в 1782 году в рамках исследования вероятностей. Фактически, венгерский математик Йожеф Микса Петцваль (1807–1891) был первым, кто изучил его систематически, тогда как Лаплас использовал его только для решения своих задач. Однако работа Петцваля не привлекла внимания, в том числе потому, что один из его учеников ошибочно обвинил его в плагиате против Лапласа. Примерно через сто лет британский инженер-электрик и физик Оливер Хевисайд (1850–1925) применил операторное исчисление, которое он нашел методом проб и ошибок, для решения дифференциальных уравнений в теоретической электротехнике. Немецкий математик Густав Дойч (1892–1977) заменил это преобразованием Лапласа, разработал его математические основы и сделал преобразование Лапласа широко используемым для решения многих задач математической физики и теоретической электротехники. Описываются краевые задачи. Теория и применение преобразования Лапласа были найдены в учебниках и программах теоретической электротехники и, прежде всего, в книгах по обыкновенным уравнениям и уравнениям в частных производных, по крайней мере, с начала 1960-х годов. Примеры функций, для которых существует интеграл Лапласа, перечислены в таблицах соответствий ниже. Указанных условий достаточно только для существования интеграла Лапласа. Если они не выполняются, необходимо провести дополнительные исследования. В качестве примера рассмотрим обратное преобразование дробно-рациональных функций: для спектральной функции может быть выполнено с (табличным, здесь примерно вычисленным) соответствием Задайте обратное преобразование напрямую как можно нанести на карту. Решения преобразованных задач гораздо легче найти в области изображения, чем в исходной области. В особых случаях таким же образом могут быть решены линейные дифференциальные уравнения с полиномиальными коэффициентами. Недостатком является обычно сложное обратное преобразование. Это интегральное преобразование иногда называют односторонним преобразованием Фурье. Еще одним важным свойством преобразования Лапласа функций реального времени является сопряженная симметрия в области комплексного изображения. Ф. ( s ¯ ) знак равно Ф. ¯ ( s ) <\ Displaystyle F (<\ bar или разделены на действительную и мнимую части Преобразование Лапласа образует функцию конечного времени В приложениях преобразования Лапласа размерность также является преобразованием Лапласа. Ниже показано решение задачи начального значения обыкновенного дифференциального уравнения первого порядка с постоянными коэффициентами с использованием преобразования Лапласа: d d т ж ( т ) + λ ж ( т ) знак равно 0 <\ Displaystyle <\ гидроразрыва <\ mathrm Вышеупомянутое дифференциальное уравнение описывает простые процессы роста и уменьшения и, следовательно, может быть обнаружено во многих областях, в том числе. в естественных, экономических и социальных науках. Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими. Преобразованием Лапласа функции действительной переменной Правая часть этого выражения называется интегралом Лапласа. Обратным преобразованием Лапласа функции комплексного переменного где Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции Двусторонее преобразование Лапласа определяется следующим образом: Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций. Пусть Если применить следующую замену переменных: Преобразование Лапласа Примечание: это достаточные условия существования. Для существования обратного преобразования Лапласа достаточно выполнение следующих условий: 1. Если изображение F(s) — аналитичная функция для 2. Пусть Примечание: это достаточные условия существования. Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов. Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем. Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа. Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала деленное на свой аргумент. Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком. Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, деленный на свой аргумент. Теоремы о начальном и конечном значении (предельные теоремы): Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, к примеру, используется для анализа устойчивости траектории динамической системы. Умножение на число Ниже представлена таблица преобразования Лапласа для некоторых функций. Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники. Практически все интегральные преобразования имеют схожую природу и могут получаться одно из другого через выражения соответствия. Многие из них являются частными случаями других преобразований. Далее даны формулы, связывающие преобразования Лапласа с некоторыми другими функциональными преобразованиями. Преобразование Лапласа-Карсона получается из преобразования Лапласа путём домножения его на комплексную переменную. Двустороннее преобразование Лапласа Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом s = iω : Примечание: в этих выражениях опущен масштабирующий множитель Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы. Преобразование Меллина и обратное преобразование Меллина связаны с двусторонним преобразованием Лапласа простой заменой переменных. Если в преобразовании Меллина Z-преобразование — это преобразование Лапласа решётчатой функции, производимое с помощью замены переменных: где Интегральная форма преобразования Бореля идентична преобразованию Лапласа, существует также обобщённое преобразование Бореля, с помощью которого использование преобразования Лапласа распространяется на более широкий класс функций. Преобразование Абеля | Преобразования Бесселя | Преобразование Бушмана | Преобразование Гильберта | Преобразование Конторовича — Лебедева | Преобразование Лапласа | Преобразование Мейера | Преобразование Мелера — Фока | Преобразование Меллина | Преобразование Нерейна | Преобразование Радона | Преобразование Стильтьеса | Преобразование Фурье | Преобразование Хартли | Преобразование Хенкеля Лапласа преобразование — преобразование, переводящее функцию f (t) действительного переменного t (0 Большая советская энциклопедия ЛАПЛАСА ПРЕОБРАЗОВАНИЕ — трансформация Лапласа, в широком смысле интеграл Лапласа вида где интегрирование производится по нек рому контуру Lв плоскости комплексного переменного z, ставящий в соответствие функции f(z). определенной на L, аналитич. функцию… … Математическая энциклопедия ЛАПЛАСА ПРЕОБРАЗОВАНИЕ — в геометрии переход от одной фокальной сети конгруэнции к другой фокальной сети той же конгруэнции. Понятие Л. п. сети ввел Г. Дарбу (G. Darboux, 1888), обнаруживший, что аналитич. реобразование решений уравнения Лапласа где а, b, с известные… … Математическая энциклопедия Преобразование Фурье — Преобразование Фурье операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие … … Википедия Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917 го года[1]. Важнейшее свойство преобразования Радона обратимость, то есть возможность… … Википедия Преобразование Гегенбауэра — Преобразование Гегенбауэра интегральное преобразование функции : где многочлены Гегенбауэра. Если функция разлагается в обобщенный ряд Фурье по многочленам Гегенбауэра, то им … Википедия Преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются… … Википедия Преобразование — одно из основных понятий математики, возникающее при изучении соответствий между классами геометрических объектов, классами функций и т.п. Например, при геометрических исследованиях часто приходится изменять все размеры фигур в одном и… … Большая советская энциклопедия Преобразование Хенкеля — В математике, преобразование Ханкеля порядка ν функции f(r) задаётся формулой: где Jν функция Бесселя первого рода порядка ν и ν ≥ −1/2. Обратным преобразованием Ханкеля функции Fν(k) называют следующее выражение: которое можно проверить с… … ВикипедияЭто следует из леммы Жордана Преобразование Лапласа
содержание
Общий
история
определение
существование
Обратное преобразование Лапласа
утверждение
пример
Важные приложения
характеристики
Предельные наборы
Уникальность
Связь с преобразованием Фурье
Аналитические свойства
Аналитичность
Сопряженная симметрия
>) = <\ bar Конечное преобразование Лапласа
Физическое измерение
Таблицы соответствий
Общие свойства
Таблица соответствия
пример
Преобразование Лапласа для измерений
Лапласа преобразование


Содержание
Определение
Прямое преобразование Лапласа


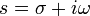
Обратное преобразование Лапласа


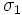
Двустороннее преобразование Лапласа

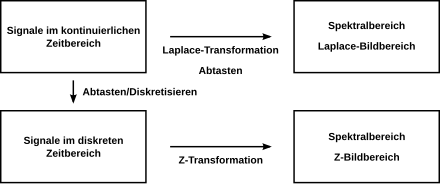
Дискретное преобразование Лапласа
Различают 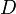
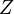
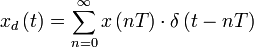
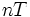
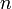
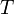
Тогда применяя преобразование Лапласа получим: 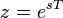
получим Z-преобразование: Свойства и теоремы
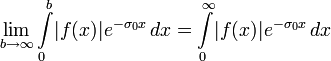
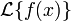
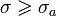
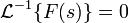
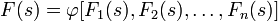
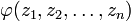
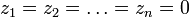
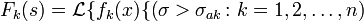
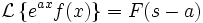
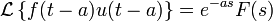
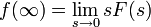
Прямое и обратное преобразование Лапласа некоторых функций
Применения преобразования Лапласа
Связь с другими преобразованиями
Фундаментальные связи
Преобразование Лапласа-Карсона
Двустороннее преобразование Лапласа
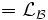
Преобразование Фурье
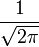
Преобразование Меллина
Z-преобразование
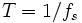
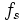
Преобразование Бореля
Библиография
См. также
Внешние ссылки
Полезное
Смотреть что такое «Лапласа преобразование» в других словарях: