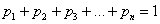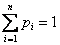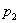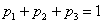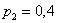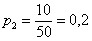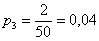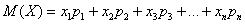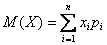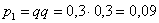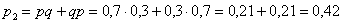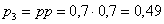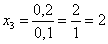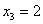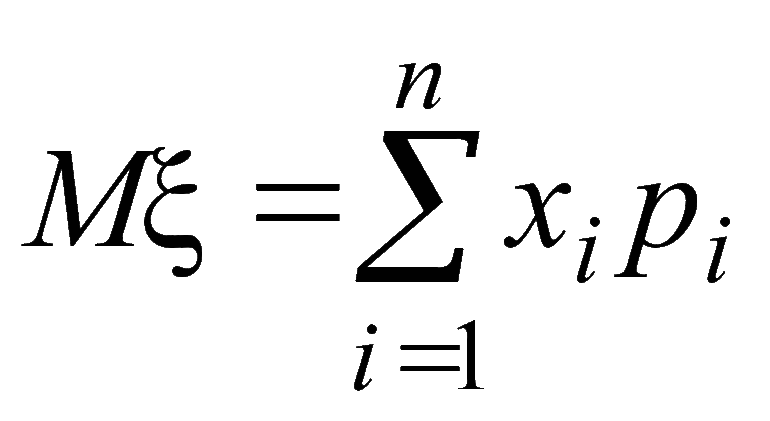в чем смысл математического ожидания
Случайные величины. Дискретная случайная величина.
Математическое ожидание
Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:
Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.
Случайные величины, как правило, обозначают через 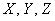
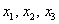
* Иногда используют 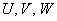
Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:
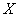
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина 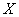
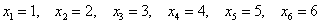
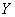
Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:
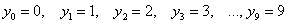
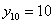
И, дабы соблюсти форму, немного физкультуры:
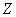
Её не в состоянии предугадать даже мастер спорта 🙂
Тем не менее, ваши гипотезы?
Коль скоро речь идёт о множестве действительных чисел, то случайная величина 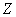
Таким образом, случайные величины целесообразно разделить на 2 большие группы:
1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.
…нарисовались непонятные термины? Срочно повторяем основы алгебры!
2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.
Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ
Сначала разберём дискретную случайную величину, затем – непрерывную.
Закон распределения дискретной случайной величины
– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей: 
Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».
А теперь очень важный момент: поскольку случайная величина 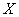
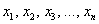
или, если записать свёрнуто:
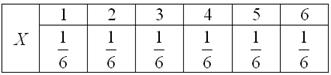
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:
Некоторая игра имеет следующий закон распределения выигрыша:
Найти
…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.
Решение: так как случайная величина 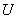
Разоблачаем «партизана»: 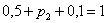
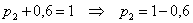
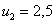
Контроль: 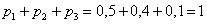
Ответ:
Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины 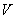
Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно 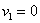
Всего таковых билетов 50 – 12 = 38, и по классическому определению:
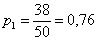
С остальными случаями всё просто. Вероятность выигрыша 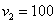
И для 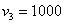
Проверка: 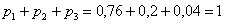
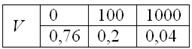
Ответ: искомый закон распределения выигрыша:
Следующее задание для самостоятельного решения:
Вероятность того, что стрелок поразит мишень, равна 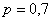
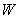
…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.
Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина 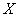
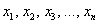
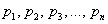
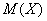
или в свёрнутом виде:
Вычислим, например, математическое ожидание случайной величины 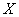
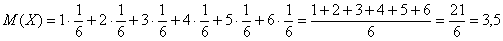
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.
Теперь вспомним нашу гипотетическую игру:
Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:
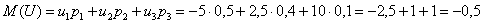
Не верь впечатлениям – верь цифрам!
Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.
Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.
Творческое задание для самостоятельного исследования:
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины 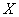
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.
Но прежде будет полезно размять пальцы на клавишах калькулятора:
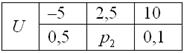
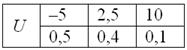
Случайная величина 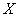
Найти 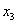
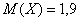
Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.
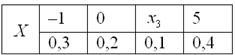
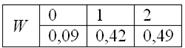
Пример 3. Решение: по условию 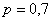
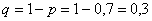
Составим 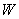
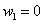
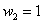
Проверка: 0,09 + 0,42 + 0,49 = 1
Ответ:
Примечание: можно было использовать обозначения 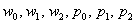
Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: 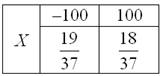
Вычислим математическое ожидание: 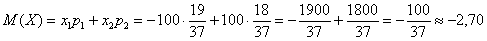
Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.
Пример 5. Решение: по определению математического ожидания: 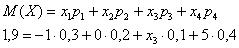
поменяем части местами и проведём упрощения: 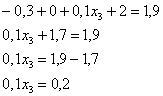
таким образом:
Выполним проверку: 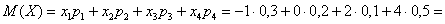
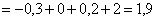
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Краткое описание
Чтобы понять смысл условного математического ожидания случайной величины, необходимо изучить ряд правил, а также ознакомится с примерами, дабы в будущем можно было избежать грубых ошибок. Одной из важнейших числовых характеристик дискретной величины является матожидание. Для изучения всех нюансов необходимо ввести понятие системы случайных процессов. Если представить значение в виде графика, то итоговое ожидание будет выступать в виде некоторого центра массы, изображённой на графике фигуры. Для решения классической задачи можно задействовать следующую формулу: Е (х) = Х1О1 + Х1О2 + … + Х n О n.
Расшифровка формулы выглядит следующим образом:
В теории вероятности специалистам удалось доказать, что среднее значение постоянной величины даже после многочисленных испытаний всё равно будет стремиться к матожиданию. В некоторых случаях результат может быть отрицательный. А это значит, что если количество итоговых испытаний слишком велико, то среднее значение обязательно будет равно матожиданию (прогноз среднего значения). Для более тщательного изучения темы специалисты рекомендуют использовать следствие (теорема с небольшим доказательством, которое следует из другой теоремы).
Гораздо проще разобраться в этой теме в том случае, если изучить наглядный пример. Если человек несколько раз бросит самый обычный шестигранный игральный кубик, и будет записывать все выпавшие значения, то при большом количестве испытаний можно получить число 3,5. Аналогичный результат будет достигнут и в том случае, если просчитать матожидание. Подсчёт выглядит следующим образом:
Правильный подход позволяет составить закон распределения случайных магнитуд выигрыша. Классическая формула математического ожидания часто используется для качественной оценки рентабельности какой-либо деятельности. Этот математический подход также используется на рынке ФОРЕКС при прогнозировании реальной суммы дохода какой-либо торговой стратегии опытных трейдеров.
Основы теории
Для случайной непрерывной величины незаменимая механическая интерпретация матожидания всегда сохраняет основное своё правило: центр массы соответствует единичной массе, которая непрерывным образом распределена на оси абсцисс g (a). В отличие от распространённой независимой величины, у которой итоговый аргумент функции х может меняться скачкообразно, у непрерывной величины аргумент таким колебаниям не подвержен.
Чтобы отыскать матожидание и дисперсию непрерывной случайной величины, обязательно нужно найти определённые интегралы. Если по условиям задачи была дана функция плотности величины непрерывного типа, то она обязательно входит в подынтегральное выражение. Когда дана функция распределения вероятностей, тогда обязательно нужно найти функцию плотности. Количество испытаний константы равно самой константе.
Арифметическое среднее всех задействованных значений непрерывной величины называется её матожиданием, что тоже нужно запомнить. Величина интеграла называется дисперсией непрерывной случайной величины.
Среднее квадратичное произведение непрерывной величины всегда определяется специалистами как арифметическое значение квадратного корня из дисперсии. Только тщательное изучение всех правил поможет решать все поставленные математические задачи без допущения ошибок.
Ключевые особенности дисперсии
За дисперсию принято понимать средний квадрат отклонений полученных значений признака от среднего арифметического числа. Для обозначения используется одна заглавная латинская буква D.
Для правильного расчёта дисперсии необходимо посчитать разность между имеющимся числом и средним арифметическим, чтобы в итоге возвести результат в квадрат. Значений получится столько, сколько может быть реальных исходов у рассматриваемого события. После этого остаётся только просуммировать все полученные данные и разделить на количество элементов в последовательности. Если максимальное количество исходов приравнивается к 5, тогда делить нужно именно на эту цифру.
У дисперсии также есть свойства, которые обязательно нужно знать, чтобы решать различные математические задачи. К примеру:
К примеру: нужно представить, что был проведён 21 эксперимент и в итоге 7 разных исходов. Первым делом нужно рассчитать среднее арифметическое: сумма элементов равняется 21. Эту цифру нужно разделить на 7. В результате получится цифра 3. После этого из каждого числа исходной последовательности нужно вычесть 3. Каждое значение возводят в квадрат, а результат слаживают вместе. Если всё сделать правильно, то в итоге можно получить 12. На финальном этапе остаётся разделить число на количество элементов.
Зависимость итога от количества экспериментов
Многочисленные свойства математического ожидания очень важны для правильного решения поставленных задач. Для изучения этой темы необходимо знать, что собой представляет квадратическое отклонение. Для обозначения этого термина используются буквы sd, либо греческая строчная «сигма». Квадратическое отклонение отображает то, насколько именно отклоняются значения от центрального признака. Если в основе лежит нахождение нужного значения, тогда следует постараться правильно рассчитать квадратный корень из дисперсии.
Можно построить график равномерного распределения, чтобы непосредственно на нём увидеть реальную величину среднего квадратного отклонения. Для этих целей необходимо выполнить несколько несложных заданий. Нужно взять половину изображения справа и слева от моды (центральное значение), дабы постараться провести перпендикуляр к горизонтальной оси так, чтобы площади получившихся фигур были абсолютно равными.
Размер отрезка между серединой распределения и получившейся проекцией на горизонтальную ось и будет самое обычное среднее квадратичное отклонение.
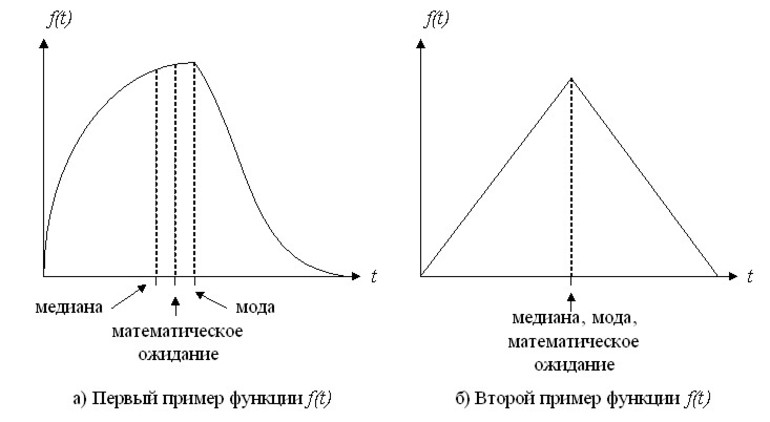
Актуальность применения медианы и моды
Математики склонны утверждать, что средние величины представляют собой своего рода отвлечённую величину. Отвлекаясь от определённых величин каждого варианта, эти числа отлично отображают общее положение, которое присуще всей совокупности единиц. В некоторых случаях можно наблюдать, что величина не имеет какого-либо равенства ни с одним из конкретных вариантов распространённых вариантов.
К примеру: среднее число членов одной семьи приравнивается к 4,85. Этот показатель был получен на основе исчисления соответствующей совокупности данных. Число не имеет ничего общего с определённым составом конкретной семьи, так как дробного числа членов семьи быть не может. В этом случае принято понимать за основу показатель средней величины состава семьи. Возле дробного числа группируются реальные варианты.
Когда стоит задача определить какую-либо абстрактную величину, тогда можно смело задействовать величины конкретных вариантов, содержащихся в рассматриваемой совокупности величин. Именно эти величины занимают определённое место в ранжированном ряду индивидуальных значений признака. Такими величинами чаще всего являются медиана, а также мода. Мода — это самая распространённая величина, которую принято обозначать символами Мо.
Мода как величина в прерывистом ряду всегда определяется на примере выявления самого большого процента мужчин, которые носят одинаковый размер обуви. После несложных математических действий можно понять, что большинство мужчин носят обувь 40 размера. А это значит, что Мо = 40, модой является сорок первый размер обуви.
А вот когда необходимо отыскать достоверную медиану, то первым делом нужно постараться найти один из центральных вариантов рассматриваемой совокупности. На примере изучаемого варианта за основу будет взят эксперимент, в котором участвовали 100 человек: 100:2 = 50. После этого по накопленным частотам выполняют определение достоверной величины пятидесятого ряда. Если следовать накопленной частотности, то полученная цифра будет находиться между 41 и 69 позициями. Это значит, что 50-й член ряда имеет величину 40 (Ме = 40-й размер обуви).
Доступное программное обеспечение
Из всех перечисленных правил и формул можно сделать вывод, что используемое математическое ожидание обозначается самым простым образом, но в этой теме нужно хорошо разбираться. Правильные расчёты дисперсии и математического ожидания — это не самая простая задача, с арифметической точки зрения.
Чтобы не тратить драгоценное время на поиски решения можно воспользоваться специальной онлайн-калькулятор, которая активно используется в высших учебных заведениях. Это программное обеспечение носит название R. В ней предусмотрено наличие специальных функций, которые позволяют рассчитать значения для многих понятий из статистики и теории вероятности.