в чем смысл комбинированного метода шифрования электронных документов
Комбинированная криптосистема шифрования
Анализ рассмотренных выше особенностей симметричных и асимметричных криптографических систем показывает, что при совместном использовании они эффективно дополняют друг друга, компенсируя недостатки.
Действительно, главным достоинством асимметричных криптосистем с открытым ключом является их потенциально высокая безопасность: нет необходимости ни передавать, ни сообщать кому-либо значения секретных ключей, ни убеждаться в их подлинности. Однако их быстродействие обычно в сотни (и более) раз меньше быстродействия симметричных криптосистем с секретным ключом.
В свою очередь, быстродействующие симметричные криптосистемы страдают существенным недостатком: обновляемый секретный ключ симметричной криптосистемы должен регулярно передаваться партнерам по информационному обмену и во время этих передач возникает опасность раскрытия секретного ключа.
Совместное использование этих криптосистем позволяет эффективно реализовывать такую базовую функцию защиты, как криптографическое закрытие передаваемой информации с целью обеспечения ее конфиденциальности. Комбинированное применение симметричного и асимметричного шифрования устраняет основные недостатки, присущие обоим методам, и позволяет сочетать преимущества высокой секретности, предоставляемые асимметричными криптосистемами с открытым ключом, с преимуществами высокой скорости работы, присущими симметричным криптосистемам с секретным ключом.
Метод комбинированного использования симметричного и асимметричного шифрования заключается в следующем.
Симметричную криптосистему применяют для шифрования исходного открытого текста, а асимметричную криптосистему с открытым ключом применяют только для шифрования секретного ключа симметричной криптосистемы. В результате асимметричная криптосистема с открытым ключом не заменяет, а лишь дополняет симметричную криптосистему с секретным ключом, позволяя повысить в целом защищенность передаваемой информации. Такой подход иногда называют схемой электронного «цифрового конверта».
Пусть пользователь А хочет использовать комбинированный метод шифрования для защищенной передачи сообщения М пользователю В.
Тогда последовательность действий пользователей А и В будет следующей.
Действия пользователя А:
1. Он создает (например, генерирует случайным образом) сеансовый секретный ключ Ks, который будет использован в алгоритме симметричного шифрования для зашифрования конкретного сообщения или цепочки сообщений.
2. Зашифровывает симметричным алгоритмом сообщение М на сеансовом секретном ключе Ks.
3. Зашифровывает асимметричным алгоритмом секретный сеансовый ключ Ks на открытом ключе Кв пользователя В (получателя сообщения).
4. Передает по открытому каналу связи в адрес пользователя В зашифрованное сообщение М вместе с зашифрованным сеансовым ключом Ks.
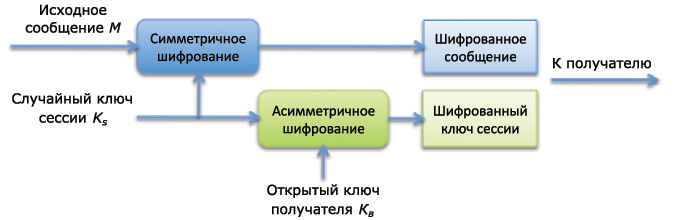
Действия пользователя А иллюстрируются схемой шифрования сообщения комбинированным методом (рис. 5.4).
Рис. 5.4. Схема шифрования сообщения комбинированным методом
Эта статья была опубликована Вторник, 11 августа, 2009 at 18:33 в рубрике Принципы криптографической защиты информации. Вы можете следить за ответами через RSS 2.0 feed.
Комбинированный метод шифрования



Главным достоинством криптосистем с открытым ключом является их потенциально высокая безопасность: нет необходимости ни передавать, ни сообщать кому бы то ни было значения секретных ключей, ни убеждаться в их подлинности. В симметричных криптосистемах существует опасность раскрытия секретного ключа во время передачи.
Oднако алгоритмы, лежащие в основе криптосистем с открытым ключом, имеют следующие недостатки:
· генерация новых секретных и открытых ключей основана на генерации новых больших простых чисел, а проверка простоты чисел занимает много процессорного времени;
· Процедуры шифрования и расшифрования, связанные с возведением в степень многозначного числа, достаточно громоздки.
Поэтому быстродействие криптосистем с открытым ключом обычно в сотни и более раз меньше быстродействия симметричных криптосистем с секретным ключом.
Комбинированный (гибридный) метод шифрования позволяет сочетать преимущества высокой секретности, предоставляемые асимметричными криптосистемами с открытым ключом, с преимуществами высокой скорости работы, присущими симметричным криптосистемам с секретным ключом. При таком подходе криптосистема с открытым ключом применяется для шифрования, передачи и последующего расшифрования только секретного ключа симметричной криптосистемы. А симметричная криптосистема применяется для шифрования и передачи исходного открытого текста. В результате криптосистема с открытым ключом не заменяет симметричную криптосистему с секретным ключом, а лишь дополняет ее, позволяя повысить в целом защищенность передаваемой информации. Такой подход иногда называют схемой электронного цифрового конверта.
Если пользователь а хочет передать зашифрованное комбинированным методом сообщение м пользователю в, то порядок его действий будет таков.
1. Создать (например, сгенерировать случайным образом) симметричный ключ, называемый в этом методе сеансовым ключом КS.
2. Зашифровать сообщение М на сеансовом ключе КS.
3. Зашифровать сеансовый ключ КS на открытом ключе КВ пользователя В.
4. Передать по открытому каналу связи в адрес пользователя В зашифрованное сообщение вместе с зашифрованным сеансовым ключом.
Действия пользователя в при получении зашифрованного сообщения и зашифрованного сеансового ключа должны быть обратными:
5. Расшифровать на своем секретном ключе kВ сеансовый ключ КS.
6. С помощью полученного сеансового ключа КS расшифровать и прочитать сообщение М.
При использовании комбинированного метода шифрования можно быть уверенным в том, что только пользователь В сможет правильно расшифровать ключ КS и прочитать сообщение М.
Таким образом, при комбинированном методе шифрования применяются криптографические ключи как симметричных, так и асимметричных криптосистем. Очевидно, выбор длин ключей для каждого типа криптосистемы следует осуществлять таким образом, чтобы злоумышленнику было одинаково трудно атаковать любой механизм защиты комбинированной криптосистемы.
В табл. 4.3. приведены распространенные длины ключей симметричных и асимметричных криптосистем, для которых трудность атаки полного перебора примерно равна трудности факто-ризации соответствующих модулей асимметричных криптосистем [121].
Комбинированный метод шифрования
Криптосистема шифрования данных RSA
Однонаправленные функции
Асимметричные криптосистемы
1. Концепция криптосистемы с открытым ключом
Для расшифровки данных получатель зашифрованной информации использует второй ключ, который является секретным. Ключ расшифровки не может быть определен без определения ключа шифрования.
2.Концепция асимметричных криптографических систем с открытым ключом основана на применении однонаправленных функций. Основным критерием отнесения функции к классу однонаправленных функций является отсутствие эффективных алгоритмов обратного преобразования.
Вторым важным классом функций, используемых при построении криптосистем с открытым ключом, являются так называемые однонаправленные функции с «потайным ходом» (с «лазейкой»). Функция относится к классу однонаправленных функций с «потайным ходом» в том случае, если она является однонаправленной и, кроме того, возможно эффективное вычисление обратной функции, если известен «потайной ход» (секретное число, строка или другая информация, ассоциирующаяся с данной функцией).
3.Алгоритм RSA предложили в 1978 г. Алгоритм получил свое название по первым буквам фамилий его авторов. Алгоритм RSA стал первым полноценным алгоритмом с открытым ключом, который может работать как в режиме шифрования данных, так и в режиме электронной цифровой подписи.
Надежность алгоритма основывается на трудности факторизации больших чисел и трудности вычисления дискретных логарифмов.
Криптосистемы RSA реализуются как аппаратным, так и программным путем.
Для аппаратной реализацииопераций шифрования и расшифровки RSA разработаны специальные процессоры. Эти процессоры, реализованные на сверхбольших интегральных схемах (СБИС), позволяют выполнять операции RSA, связанные с возведением больших чисел в колоссально большую степень по модулю N, за относительно короткое время. И все же аппаратная реализация RSA примерно в 1000 раз медленнее аппаратной реализации симметричного криптоалгоритма DES.
Программная реализацияRSA примерно в 100 раз медленнее программной реализации DES. С развитием технологии эти оценки могут несколько изменяться, но асимметричная криптосистема RSA никогда не достигнет быстродействия симметричных криптосистем.
Медлительность реализации криптосистем RSA ограничивает область их применения, но не перечеркивает их ценность.
4. Главным достоинством криптосистем с открытым ключом является их потенциально высокая безопасность: нет необходимости ни передавать, ни сообщать кому бы то ни было значения секретных ключей, ни убеждаться в их подлинности. В симметричных криптосистемах существует опасность раскрытия секретного ключа во время передачи.
Алгоритмы, лежащие в основе криптосистем с открытым ключом, имеют следующие недостатки:
• генерация новых секретных и открытых ключей основана на генерации новых больших простых чисел, а проверка простоты чисел занимает много процессорного времени;
• процедуры шифрования и расшифровки, связанные с возведением в степень многозначного числа, достаточно громоздки.
Комбинированный (гибридный) метод шифрования позволяет сочетать преимущества высокой секретности, предоставляемые асимметричными криптосистемами с открытым ключом, с преимуществами высокой скорости работы, присущими симметричным криптосистемам с секретным ключом. При таком подходе криптосистема с открытым ключом применяется для шифрования, передачи и последующей расшифровки только секретного ключа симметричной криптосистемы. А симметричная криптосистема применяется для шифрования и передачи исходного открытого текста. В результате криптосистема с открытым ключом не заменяет симметричную криптосистему с секретным ключом, а лишь дополняет ее, позволяя повысить в целом защищенность передаваемой информации. Такой подход иногда называют схемой электронного цифрового конверта.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Комбинированные методы шифрования
1. Комбинированные методы шифрования
Важнейшим требованием к системе шифрования является стойкость данной системы. К сожалению, повышение стойкости при помощи любого метода приводит, как правило, к трудностям и при шифровании открытого текста и при его расшифровке. Одним из наиболее эффективных методов повышения стойкости шифртекста является метод комбинированного шифрования. Этот метод заключается в использовании и комбинировании нескольких простых способов шифрования. Шифрование комбинированными методами основывается на результатах, полученных К.Шенноном. Наиболее часто применяются такие комбинации, как подстановка и гамма, перестановка и гамма, подстановка и перестановка, гамма и гамма. Так, например, можно использовать метод шифрования простой перестановкой в сочетании с методом аналитических преобразований или текст, зашифрованный методом гаммирования, дополнительно защитить при помощи подстановки.
Рассмотрим несколько примеров:
Пример 1. Возьмем в качестве открытого текста сообщение: «Я пишу курсовую».
Защитим этот текст методом простой перестановки, используя в качестве ключа слово «зачет» и обозначая пробел буквой «ь». Выписываем буквы открытого текста под буквами ключа. Затем буквы ключа расставляем в алфавитном порядке. Выписываем буквы по столбцам и получаем шифртекст: ььоиууяусшрюпкв.
Полученное сообщение зашифруем с помощью метода подстановки:
Итак, имея открытый текст: «Я пишу курсовую», после преобразований получаем шифртекст: ююркххбхуьтасмд, используя методы перестановки и замены. Раскрыть текст расшифровщик сможет, зная, что ключами являются число 2 и слово «зачет» и соответственно последовательность их применения.
Пример 2. В качестве примера также рассмотрим шифр, предложенный Д. Френдбергом, который комбинирует многоалфавитную подстановку с генератором псевдослучайных чисел. Особенность данного алгоритма состоит в том, что при большом объеме шифртекста частотные характеристики символов шифртекста близки к равномерному распределению независимо от содержания открытого текста.
1. Установление начального состояния генератора псевдослучайных чисел.
2. Установление начального списка подстановки.
3. Все символы открытого текста зашифрованы?
5. Осуществление замены.
6. Генерация случайного числа.
7. Перестановка местами знаков в списке замены.
8. Переход на шаг 4.
Пример 3. Открытый текст: «АБРАКАДАБРА».
Используем одноалфавитную замену согласно таблице 1.
| А | Б | Д | К | Р |
| X | V | N | R | S |
Последовательность чисел, вырабатываемая датчиком: 31412543125.
После перестановки символов исходного алфавита получаем таблицу 2 (h1=3).
| Д | Б | А | К | Р |
| X | V | N | R | S |
2. у2=V. Таблица 2 после перестановки (h2=1) принимает вид, представленный в таблице 3.
| Б | Д | А | К | Р |
| X | V | N | R | S |
Осуществляя дальнейшие преобразования в соответствии с алгоритмом Френдберга, получаем шифртекст: «XVSNSXXSSSN».
Одной из разновидностей метода гаммирования является наиболее часто применяемый метод многократного наложения гамм. Необходимо отметить, что если уi=Гk(Г1(xi)), то Гk(Г1(xi))=Г1(Гk(xi)). (1*)
Тождество (1*) называют основным свойством гаммы.
Пример 4. Открытый текст: «ШИФРЫ»(25 09 21 17 28»);
Г1= «ГАММА» («04 01 13 13 01»);
Г2 = «ТЕКСТ» («19 06 11 18 19»), согласно таблице 1.
Используемая операция: сложение по mod 2.
11001 01001 10101 10001 11100
00100 00001 01101 01101 00001
11101 01000 11000 11100 11101.
11101 01000 11000 11100 11101
10011 00110 01011 10010 10011
01110 01110 10011 01110 01110.
Проведем операцию шифрования, поменяв порядок применения гамм.
11001 01001 10101 10001 11100
10011 00110 01011 10010 10011
01010 01111 11110 00011 01111.
01010 01111 11110 00011 01111
00100 00001 01101 01101 00001
01110 01110 10011 01110 01110.
Таким образом, y2i=y2i’, что является подтверждением основного свойства гаммы.
При составлении комбинированных шифров необходимо проявлять осторожность, так как неправильный выбор составлявших шифров может привести к исходному открытому тексту. Простейшим примером служит наложение одной гаммы дважды.
Пример 5. Открытый текст: «ШИФРЫ»(«25 09 21 17 28»);
Г1 = Г2= «ГАММА» («04 01 13 13 01»), согласно таблице 1.
Используемая операция: сложение по mod 2:
11001 01001 10101 10001 11100
00100 00001 01101 01101 00001
00100 00001 01101 01101 00001
11001 01001 10101 10001 11100.
Таким образом, результат шифрования представляет собой открытый текст.
2. Теория проектирования блочных шифров
К. Шеннон выдвинул понятия рассеивания и перемешивания. Спустя пятьдесят лет после формулирования этих принципов, они остаются краеугольным камнем проектирования хороших блочных шифров.
Перемешивание маскирует взаимосвязи между открытым текстом, шифртекстом и ключом. Даже незначительная зависимость между этими тремя составляющими может быть использована в дифференциальном и линейном криптоанализе. Хорошее перемешивание настолько усложняет статистику взаимосвязей, что пасуют даже мощные криптоаналитические средства.
Рассеивание распространяет влияние отдельных битов открытого текста на возможно больший объем шифртекста. Это тоже маскирует статистические взаимосвязи и усложняет криптоанализ.
Для обеспечения надежности достаточно только перемешивания. Алгоритм, состоящий из единственной, зависимой от ключа таблицы подстановок 64 бит открытого текста в 64 бит шифртекста был бы достаточно надежным. Недостаток в том, что для хранения такой таблицы потребовалось бы слишком много памяти: 10 20 байт. Смысл создания блочного шифра и состоит в создании чего-то подобного такой таблице, но предъявляющего к памяти более умеренные требования.
Тонкость, состоит в том, что в одном шифре следует периодически перемежать в различных комбинациях перемешивание (с гораздо меньшими таблицами) и рассеивание. Такой шифр называют составным шифром (product cipher). Иногда блочный шифр, который использует последовательные перестановки и подстановки, называют сетью перестановок-подстановок, или SP-сетью.
Кроме того, на примере DES можно продемонстрировать еще несколько принципов проектирования блочных шифров. Первый принцип реализует идею итеративного блочного шифра. При этом предполагается, что простая функция раунда последовательно используется несколько раз. Двухраундовый алгоритм DES слишком ненадежен, чтобы все биты результата зависели от всех битов ключа и всех битов исходных данных. Для этого необходимо 5 раундов. Весьма надежен 16-раундовый алгоритм DES, а 32-раундовый DES еще более стоек.
В чем смысл комбинированного метода шифрования электронных документов
8. КОМБИНИРОВАННЫЕ ШИФРЫ
8.1. Шифры ADFGX и ADFGVX
Комбинированные (составные) шифры предполагают использование для шифрования сообщения сразу нескольких методов (например, сначала замена символов, а затем их перестановка).
Таблица шифрозамен ADFGX представляет собой матрицу 5 х 5, а для ADFGVX – 6 х 6. Строки и столбцы обозначаются буквами, входящими в название шифра. Пример таблицы шифрозамен для шифра ADFGVX применительно к русскому алфавиту показан на следующем рисунке.
| A | D | F | G | V | X | |
| A | Ю | У | И | Ч | К | Б |
| D | В | Г | Е | Ф | Ж | З |
| F | Й | А | Л | М | О | П |
| G | Р | Щ | Т | Я | Ё | Х |
| V | Ц | Н | Ш | С | Ъ | Ы |
| X | Ь | Э | Д | — | — | — |
Рис.8.1. Пример таблицы шифрозамен для шифра ADFGVX
Шифрозамена для буквы исходного текста состоит из букв, обозначающих строку и столбец, на пересечении которых она находится (см. шифр «Полибианский квадрат»). Например, для сообщения «АБРАМОВ» набор шифрозамен будет «FD AX GA FD FG FV DA».
На втором этапе для выполнения перестановки полученный набор шифрозамен вписывается построчно сверху-вниз в таблицу, количество столбцов в которой строго определено (ADFGX) или соответствует количеству букв в ключевом слове (ADFGVX). Нумерация столбов либо оговаривается сторонами (ADFGX) либо соответствует положению букв ключевого слова в алфавите, как в шифре вертикальной перестановки (ADFGVX). Например, для полученного выше набора шифрозамен перестановочная таблица с ключевым словом «ДЯДИНА» показана на следующем рисунке.
Рис.8.2. Перестановочная таблица шифра ADFGVX с ключевым словом «ДЯДИНА»
На третьем этапе буквы выписываются из столбцов в соответствии с их нумерацией, при этом считывание происходит по столбцам, а буквы объединяются в пятибуквенные группы. Таким образом, окончательная шифрограмма для рассматриваемого примера будет выглядеть «AVFFD AFXGG FDDA».
8.2. Основы блочного комбинированного шифрования
Среди комбинированных методов шифрования наиболее распространенными являются методы блочного шифрования. Блочное шифрование предполагает разбиение исходного открытого текста на равные блоки, к которым применяется однотипная процедура шифрования. В настоящее время блочные шифры широко используются на практике. Российский и бывший американский стандарты шифрования (DES) относятся именно к этому классу шифров. В основе шифров лежат так называемые «сети Фейстеля» [17]. В 1971 г. Хорст Фейстель (Horst Feistel) запатентовал два устройства с различными алгоритмами шифрования, названные затем общим именем «Люцифер» (Lucifer). Одно из устройств использовало конструкцию, впоследствии названную «сетью Фейстеля» («Feistel cipher», «Feistel network»). Работа над созданием новых криптосистем велась им в стенах IBM вместе с Доном Копперсмитом (Don Coppersmith). Проект «Люцифер» был скорее экспериментальным, но стал базисом для алгоритма Data Encryption Standard (DES). В 1977 г. DES стал стандартом в США на шифрование данных вплоть до 2001 г. и до последнего времени широко использовался в криптографических системах.
Сеть Фейстеля состоит из нескольких ячеек.
Рис.8.3. Ячейка Фейстеля
В общем виде, центральная часть блочных шифров, основанных на сетях Фейстеля, выглядит следующим образом.
Рис.8.4. Сеть Фейстеля
Как видно, процедуры зашифрования и расшифрования полностью идентичны, за исключением порядка использования ключевых элементов ki. При этом функция шифрования f может быть сколь угодно сложной и не обязательно обратимой. Обратимость гарантирует сама конструкция сети.
Шифрование при помощи данной конструкции легко реализуется как на программном уровне, так и на аппаратном, что обеспечивает широкие возможности применения. На основе сетей Фейстеля разработано большое количество шифров, среди которых: DES, ГОСТ 28147-89, Blowfish, CAST, FEAL, IDEA, Khufu, Twofish и многие другие.
В алгоритме, лежащем в основе DES, используются методы замены, перестановки и гаммирования (сложение по модулю 2).
Открытое сообщение разбивается на блоки длиной 64 бита. Если длина сообщения не кратна 64, оно дополняется справа недостающим количеством битов.
Данные шифруются ключом длиной 56 битов. На самом деле ключ имеет размер 64 бита, однако реально для выработки ключевых элементов используются только 56 из них. Самые младшие биты каждого байта ключа (8-ой, 16-ый, …, 64-ый) не попадают в ключевые элементы и служат исключительно для контроля четности. Требуется, чтобы сумма битов каждого байта ключа, включая контрольный, была нечетной (нечетный паритетный бит).
Для решения разнообразных криптографических задач, разработаны четыре рабочих режима, реализующих DES:
Открытое сообщение разбивают на 64-битовые блоки. Каждый из них шифруют независимо с использованием одного и того же ключа шифрования.
Общая схема шифрования блока изображена на рис.8.5 [24].
Рис.8.5. Схема шифрования блока
1. Шифрование 64-битового блока данных T начинается с начальной перестановки битов IP.
Таблица 8.1. Начальная перестановка IP
| 58 | 50 | 42 | 34 | 26 | 18 | 10 | 2 |
| 60 | 52 | 44 | 36 | 28 | 20 | 12 | 4 |
| 62 | 54 | 46 | 38 | 30 | 22 | 14 | 6 |
| 64 | 56 | 48 | 40 | 32 | 24 | 16 | 8 |
| 57 | 49 | 41 | 33 | 25 | 17 | 9 | 1 |
| 59 | 51 | 43 | 35 | 27 | 19 | 11 | 3 |
| 61 | 53 | 45 | 37 | 29 | 21 | 13 | 5 |
| 63 | 55 | 47 | 39 | 31 | 23 | 15 | 7 |
В таблице указывается новое положение соответствующего бита. Таким образом, при выполнении начальной перестановки 58-ый бит станет 1-ым, 50-ый – 2-ым, 42-ой – 3-им и т.д.
2. Результат перестановки Т* разделяется на две 32-битовые части H1 и L1, с которыми выполняются 16 раундов преобразования.
3. В каждом раунде i старшая половина Hi блока модифицируется путем побитового прибавления к ней по модулю 2 ( ⊕ ) результата вычисления функции шифрования f, зависящей от младшей половины блока Li и 48-битового ключевого элемента ki. Ключевой элемент ki вырабатывается из ключа шифрования. Между раундами старшая и младшая половины блока меняются местами. В последнем раунде происходит то же самое, за исключением обмена значениями половинок блока.
Таблица 8.2. Конечная перестановка IP –1
| 40 | 8 | 48 | 16 | 56 | 24 | 64 | 32 |
| 39 | 7 | 47 | 15 | 55 | 23 | 63 | 31 |
| 38 | 6 | 46 | 14 | 54 | 22 | 62 | 30 |
| 37 | 5 | 45 | 13 | 53 | 21 | 61 | 29 |
| 36 | 4 | 44 | 12 | 52 | 20 | 60 | 28 |
| 35 | 3 | 43 | 11 | 51 | 19 | 59 | 27 |
| 34 | 2 | 42 | 10 | 50 | 18 | 58 | 26 |
| 33 | 1 | 41 | 9 | 49 | 17 | 57 | 25 |
Результат последней операции и является выходным значением цикла шифрования – зашифрованным блоком С.
Все перестановки в таблицах IP и IP –1 подобраны разработчиками таким образом, чтобы максимально затруднить процесс расшифровки путём подбора ключа.
Схема функции шифрования f приведена на рис.8.6.
Рис.8.6. Схема функции шифрования
1. На вход поступает 32-битовая половина шифруемого блока Li и 48-битовый ключевой элемент ki.
2. Li разбивается на 8 тетрад по 4 бита. Каждая тетрада по циклическому закону дополняется крайними битами из соседних тетрад до 6-битного слова (функция расширения Е). Цикличность означает, что первый бит Li добавляется последним в последнее слово, а последний бит Li добавляется первым в первое слово. Далее выполняется объединение тетрад в 48-битный блок X. Например, Li = 0111 0110 1… …0 11012, тогда X = 101110 101101 … 0110102.
3. Х побитово суммируется по модулю 2 ( ⊕ ) с ключевым элементом ki.
4. 48-битовый блок данных H разделяется на восемь 6-битовых элементов, обозначенных h1, h2, …, h8.
5. Каждое из значений hj преобразуется в новое 4-битовое значение tj с помощью соответствующего узла замены Sj.
Таблица 8.3. Значения tj
| Узел замены | Номер строки | Номер столбца | |||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | ||
| S1 | 0 | 14 | 4 | 13 | 1 | 2 | 15 | 11 | 8 | 3 | 10 | 6 | 12 | 5 | 9 | 0 | 7 |
| 1 | 0 | 15 | 7 | 4 | 14 | 2 | 13 | 1 | 10 | 6 | 12 | 11 | 9 | 5 | 3 | 8 | |
| 2 | 4 | 1 | 14 | 8 | 13 | 6 | 2 | 11 | 15 | 12 | 9 | 7 | 3 | 10 | 5 | 0 | |
| 3 | 15 | 12 | 8 | 2 | 4 | 9 | 1 | 7 | 5 | 11 | 3 | 14 | 10 | 0 | 6 | 13 | |
| S2 | 0 | 15 | 1 | 8 | 14 | 6 | 11 | 3 | 4 | 9 | 7 | 2 | 13 | 12 | 0 | 5 | 10 |
| 1 | 3 | 13 | 4 | 7 | 15 | 2 | 8 | 14 | 12 | 0 | 1 | 10 | 6 | 9 | 11 | 5 | |
| 2 | 0 | 14 | 7 | 11 | 10 | 4 | 13 | 1 | 5 | 8 | 12 | 6 | 9 | 3 | 2 | 15 | |
| 3 | 13 | 8 | 10 | 1 | 3 | 15 | 4 | 2 | 11 | 6 | 7 | 12 | 0 | 5 | 14 | 9 | |
| S3 | 0 | 10 | 0 | 9 | 14 | 6 | 3 | 15 | 5 | 1 | 13 | 12 | 7 | 11 | 4 | 2 | 8 |
| 1 | 13 | 7 | 0 | 9 | 3 | 4 | 6 | 10 | 2 | 8 | 5 | 14 | 12 | 11 | 15 | 1 | |
| 2 | 13 | 6 | 4 | 9 | 8 | 15 | 3 | 0 | 11 | 1 | 2 | 12 | 5 | 10 | 14 | 7 | |
| 3 | 1 | 10 | 13 | 0 | 6 | 9 | 8 | 7 | 4 | 15 | 14 | 3 | 11 | 5 | 2 | 12 | |
| S4 | 0 | 7 | 13 | 14 | 3 | 0 | 6 | 9 | 10 | 1 | 2 | 8 | 5 | 11 | 12 | 4 | 15 |
| 1 | 13 | 8 | 11 | 5 | 6 | 15 | 0 | 3 | 4 | 7 | 2 | 12 | 1 | 10 | 14 | 9 | |
| 2 | 10 | 6 | 9 | 0 | 12 | 11 | 7 | 13 | 15 | 1 | 3 | 14 | 5 | 2 | 8 | 4 | |
| 3 | 3 | 15 | 0 | 6 | 10 | 1 | 13 | 8 | 9 | 4 | 5 | 11 | 12 | 7 | 2 | 14 | |
| S5 | 0 | 2 | 12 | 4 | 1 | 7 | 10 | 11 | 6 | 8 | 5 | 3 | 15 | 13 | 0 | 14 | 9 |
| 1 | 14 | 11 | 2 | 12 | 4 | 7 | 13 | 1 | 5 | 0 | 15 | 10 | 3 | 9 | 8 | 6 | |
| 2 | 4 | 2 | 1 | 11 | 10 | 13 | 7 | 8 | 15 | 9 | 12 | 5 | 6 | 3 | 0 | 14 | |
| 3 | 11 | 8 | 12 | 7 | 1 | 14 | 2 | 13 | 6 | 15 | 0 | 9 | 10 | 4 | 5 | 3 | |
| S6 | 0 | 12 | 1 | 10 | 15 | 9 | 2 | 6 | 8 | 0 | 13 | 3 | 4 | 14 | 7 | 5 | 11 |
| 1 | 10 | 15 | 4 | 2 | 7 | 12 | 9 | 5 | 6 | 1 | 13 | 14 | 0 | 11 | 3 | 8 | |
| 2 | 9 | 14 | 15 | 5 | 2 | 8 | 12 | 3 | 7 | 0 | 4 | 10 | 1 | 13 | 11 | 6 | |
| 3 | 4 | 3 | 2 | 12 | 9 | 5 | 15 | 10 | 11 | 14 | 1 | 7 | 6 | 0 | 8 | 13 | |
| S7 | 0 | 4 | 11 | 2 | 14 | 15 | 0 | 8 | 13 | 3 | 12 | 9 | 7 | 5 | 10 | 6 | 1 |
| 1 | 13 | 0 | 11 | 7 | 4 | 9 | 1 | 10 | 14 | 3 | 5 | 12 | 2 | 15 | 8 | 6 | |
| 2 | 1 | 4 | 11 | 13 | 12 | 3 | 7 | 14 | 10 | 15 | 6 | 8 | 0 | 5 | 9 | 2 | |
| 3 | 6 | 11 | 13 | 8 | 1 | 4 | 10 | 7 | 9 | 5 | 0 | 15 | 14 | 2 | 3 | 12 | |
| S8 | 0 | 13 | 2 | 8 | 4 | 6 | 15 | 11 | 1 | 10 | 9 | 3 | 14 | 5 | 0 | 12 | 7 |
| 1 | 1 | 15 | 13 | 8 | 10 | 3 | 7 | 4 | 12 | 5 | 6 | 11 | 0 | 14 | 9 | 2 | |
| 2 | 7 | 11 | 4 | 1 | 9 | 12 | 14 | 2 | 0 | 6 | 10 | 13 | 15 | 3 | 5 | 8 | |
| 3 | 2 | 1 | 14 | 7 | 4 | 10 | 8 | 13 | 15 | 12 | 9 | 0 | 3 | 5 | 6 | 11 | |
6. Полученные восемь элементов tj вновь объединяются в 32-битовый блок H’.
7. В H’ выполняется перестановка битов P.
Таблица 8.4. Перестановка P
| 16 | 7 | 20 | 21 | 29 | 12 | 28 | 17 |
| 1 | 15 | 23 | 26 | 5 | 18 | 31 | 10 |
| 2 | 8 | 24 | 14 | 32 | 27 | 3 | 9 |
| 19 | 13 | 30 | 6 | 22 | 11 | 4 | 25 |
Результат последней операции и является выходным значением функции шифрования Li’.
Ключевые элементы вырабатываются из ключа с использованием сдвигов и битовых выборок-перестановок. Таким образом, ключевые элементы состоят исключительно из битов исходного ключа, «перетасованных» в различном порядке. Схема выработки ключевых элементов показана на следующем рисунке.
Рис.8.7. Схема выработки ключевых элементов
1. Выработка ключевых элементов из ключа K начинается со входной выборки-перестановки битов PC1, которая отбирает 56 из 64 битов ключа и располагает их в другом порядке.
Таблица 8.5. Перестановка PC1
| 57 | 49 | 41 | 33 | 25 | 17 | 9 |
| 1 | 58 | 50 | 42 | 34 | 26 | 18 |
| 10 | 2 | 59 | 51 | 43 | 35 | 27 |
| 19 | 11 | 3 | 60 | 52 | 44 | 36 |
| 63 | 55 | 47 | 39 | 31 | 23 | 15 |
| 7 | 62 | 54 | 46 | 38 | 30 | 22 |
| 14 | 6 | 61 | 53 | 45 | 37 | 29 |
| 21 | 13 | 5 | 28 | 20 | 12 | 4 |
2. Результат выборки-перестановки K* разделяется на две 28-битовые части: старшую H1 и младшую L1.
3. 16 раз выполняется процедура.
3а. В зависимости от номера итерации обе части циклически сдвигаются на 1 или 2 бита влево.
Таблица 8.6. Циклический сдвиг
| Номер итерации | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Сдвиг (бит) | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 1 |
3б. После сдвига части объединяются и из них с помощью выборки-перестановки PC2 отбираются 48 битов, которые и формируют очередной ключевой элемент.
Таблица 8.7. Перестановка PC2
| 14 | 17 | 11 | 24 | 1 | 5 |
| 3 | 28 | 15 | 6 | 21 | 10 |
| 23 | 19 | 12 | 4 | 26 | 8 |
| 16 | 7 | 27 | 20 | 13 | 2 |
| 41 | 52 | 31 | 37 | 47 | 55 |
| 30 | 40 | 51 | 45 | 33 | 48 |
| 44 | 49 | 39 | 56 | 34 | 53 |
| 46 | 42 | 50 | 36 | 29 | 32 |
Алгоритмы шифрования и расшифрования DES-ECB в общем виде выражаются следующими схемами
Как видно схема алгоритма остается неизменной, меняется лишь порядок использования ключевых элементов. Таким образом, для расшифрования необходимо «прогнать» DES с тем же ключом, но использовать ключевые элементы в обратном порядке.
Использование различных методов шифрования:
Из-за небольшого числа возможных ключей (всего 2 56 ), появляется возможность их полного перебора на быстродействующей вычислительной технике за реальное время. В 1998 г. Electronic Frontier Foundation, используя специальный компьютер DES-Cracker, удалось взломать DES за 3 дня. По неподтвержденным данным Агентство национальной безопасности США уже в 1996 г. могло вскрывать ключ DES за 3-15 мин. с помощью устройства стоимостью 50000 долларов.
Схемы алгоритмов представлены на следующем рисунке. По каждой из стрелок передается 64 бита информации.
Рис.8.8. Схемы алгоритмов DES в режиме сцепления блоков шифра (CBC)
3. Полученная сумма затем шифруется с использованием ключа DES.
4. 64-битовый шифр C1 складывается по модулю 2 со вторым блоком текста, ре¬зультат шифруется и получается второй 64-битовый шифр С2, и т.д.
Очевидно, что последний 64-битовый блок шифртекста является функцией секретного ключа, начального вектора и каждого бита открытого текста независимо от его длины. Этот блок шифртекста называют кодом аутентификации сообщения (КАС). Код КАС может быть легко проверен получателем, владеющим секретным ключом и начальным вектором, путем повторения процедуры, выполненной отправителем. Достоинство данного режима в том, что он не позволяет накапливаться ошибкам при передаче. Блок Ti является функцией только Сi-1 и Ci. Поэтому ошибка при передаче приведет к потере только двух блоков исходного текста.
В алгоритмах CFB и OFB используется такой же подход, что и в алгоритме CBC, когда результат шифрования (расшифрования) блока на предыдущем шаге используется для шифровки (расшифровки) очередного блока. В этих режимах размер входного блока может быть меньше 64 бит.
Рис.8.9. Схемы алгоритмов DES в режимах CFB и OFB
2. Синхропосылка шифруется с использованием ключа DES.
3. Из полученного результата выбираются старшие k бит, которые складываются с блоком открытого текста Ti по модулю 2 для получения шифртекста Сi.
4. Процедура повторяется до тех пор, пока не будут обработаны все блоки текста. При этом, содержимое входного блока сдвигается на k бит влево (причем сдвиг не циклический) и младшие k бит заполняются либо шифртекстом (CFB), либо старшими k бит выходного блока (OFB).
Алгоритм расшифрования аналогичен алгоритму шифрования и отличается только входом и выходом стрелок в блок сложения по модулю 2.
При тройном DES текст шифруется 3 раза DES. Таким образом, длина ключа возрастает до 168-бит (56×3). Однако, применение тройного DES не всегда означает увеличение уровня безопасности сообщения.
Типы тройного шифрования DES:
— DES-EEE3: Шифруется 3 раза с 3 различными ключами.
— DES-EDE3: 3 DES операции шифровка-расшифровка-шифровка с 3 различными ключами.
— DES-EEE2 и DES-EDE2: Как и предыдущие, за исключением того, что первая и третья операции используют одинаковый ключ.
Сферы применения разных режимов DES.
| оригинальная битовая карта изображения | криптограмма в режиме ECB (сохранились статистические особенности) | другие режимы шифрования (псевдослучайная последовательность) |
Рис.8.10. Сохранение статистических особенностей открытого текста
Сцепление блоков шифра СВС и тройной DES могут использоваться для шифрование больших объемов данных (в частности тройной DES используется для эмиссии и обработки кредитных карт VISA, EuroPay и других платежных систем).
Обратная связь по шифртексту CFB и обратная связь по выходу OFB рекомендуется для шифрования отдельных символов или небольших сообщений.
В алгоритме, лежащем в основе ГОСТ, используются методы замены, перестановки и гаммирования (сложение по модулю 2 и 2 32 ).
Открытое сообщение разбивается на блоки длиной 64 бита. Если длина сообщения не кратна 64, оно дополняется справа недостающим количеством битов.
Длина ключа – 256 битов.
— гаммирования с обратной связью;
Режим простой замены.
Открытое сообщение разбивают на 64-битовые блоки. Каждый из них шифруют независимо с использованием одного и того же ключа шифрования. Перед шифрованием 256-битный ключ разбивается на восемь 32-битных ключевых элементов (блоков) k1, k2, …, k8.
Общая схема шифрования блока изображена на следующем рисунке.
Рис.8.11. Схема шифрования блока
1. Шифрование 64-битового блока данных T начинается с его разбиения на две 32-битовые части H1 и L1, с которыми выполняются 32 раунда преобразования.
2. В каждом раунде i:
2.1. Младшая половина Li складывается с ключевым элементом ki по модулю 2 32 ( ⊞ ).
Порядок использования ключевых элементов указан в следующей таблице.
Таблица 8.8. Порядок использования ключевых элементов
| Раунд | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Ключевой элемент | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Раунд | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| Ключевой элемент | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
2.2. Результат сложения Xi разбивается на восемь 4-битных фрагментов xij (j = 1..8), каждый из которых поступает на вход своего S-блока (узла замены) и заменяется на другой 4-битовый фрагмент yij (j = 1..8). В самом ГОСТ S-блоки не приведены. Указывается только, что они должны быть откуда-то взяты. В ГОСТ Р 34.11-94 «Информационная технология. Криптографическая защита информации. Функция хэширования» в приложении А приведены «проверочные» S-блоки, которые использовал ЦБ РФ в своих приложениях.
Таблица 8.9. Значения yij
| S-блок (Sj) | Значение xij | |||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| S1 | 4 | 10 | 9 | 2 | 13 | 8 | 0 | 14 | 6 | 11 | 1 | 12 | 7 | 15 | 5 | 3 |
| S2 | 14 | 11 | 4 | 12 | 6 | 13 | 15 | 10 | 2 | 3 | 8 | 1 | 0 | 7 | 5 | 9 |
| S3 | 5 | 8 | 1 | 13 | 10 | 3 | 4 | 2 | 14 | 15 | 12 | 7 | 6 | 0 | 9 | 11 |
| S4 | 7 | 13 | 10 | 1 | 0 | 8 | 9 | 15 | 14 | 4 | 6 | 12 | 11 | 2 | 5 | 3 |
| S5 | 6 | 12 | 7 | 1 | 5 | 15 | 13 | 8 | 4 | 10 | 9 | 14 | 0 | 3 | 11 | 2 |
| S6 | 4 | 11 | 10 | 0 | 7 | 2 | 1 | 13 | 3 | 6 | 8 | 5 | 9 | 12 | 15 | 14 |
| S7 | 13 | 11 | 4 | 1 | 3 | 15 | 5 | 9 | 0 | 10 | 14 | 7 | 6 | 8 | 2 | 12 |
| S8 | 1 | 15 | 13 | 0 | 5 | 7 | 10 | 4 | 9 | 2 | 3 | 14 | 6 | 11 | 8 | 12 |
Так, если третий фрагмент xi3 = 610 (01102), то он заменяется на yi3 = 410 (01002).
2.3. Замененные фрагменты yij объединяются обратно в 32-битовый блок Yi. После чего выполняется циклический сдвиг влево на 11 бит – Zi = Yi ⊕ ) результата сдвига Zi.
2.5. Между раундами старшая и младшая половины блока меняются местами.
3. Полублоки H33 и L33 объединяются в зашифрованный блок С.
Расшифрование отличается зашифрования обратным порядком использования ключевых элементов, представленного в табл.8.8.
Использование различных методов шифрования:
— гаммирование – по модулю 2 32 ( ⊞ ) и 2 ( ⊕ ).
Основные различия между DES и ГОСТ [8]:
— DES использует сложную процедуру для генерации подключей из ключей. В ГОСТ эта процедура очень проста;
— у S-блоков DES 6-битовые входы и 4-битовые выходы, а у S-блоков ГОСТ 4-битовые входы и выходы. В обоих алгоритмах используется по восемь S-блоков;
— в DES используются перестановка, названная Р-блоком, а в ГОСТ используется 11-битовый циклический сдвиг влево;
По мнению одного из авторитетных специалистов в области криптографии Брюса Шнайера увеличенная длина ключа и использование в вдвое больше раундов шифрования делает ГОСТ
… более устойчивым к дифференциальному и линейному криптоанализу, чем DES. … Разработчики ГОСТ пытались достигнуть равновесия между безопасностью и эффективностью. Они изменили идеологию DES так, чтобы создать алгоритм, который больше подходит для программной реализации. Они, по видимому, менее уверены в безопасности своего алгоритма и попытались скомпенсировать это очень большой длиной ключа, сохранением в секрете S-блоков и удвоением количества итераций. Вопрос, увенчались ли их усилия созданием более безопасного, чем DES, алгоритма, остается открытым.
По типу относится к подстановочно-перестановочным сетям (англ. Substitution-Permutation network, SP-сеть). В алгоритме используются методы замены, перестановки и гаммирования (сложение по модулю 2).
Основные параметры AES приведены в следующей таблицы.
Таблица 8.10. Основные параметры AES
| Тип шифра | Длина ключа Nk, битов (слов 1 ) | Размер блока зашифрования / расшифрования Nb, битов (слов) | Количество раундов Nr | Количество ключевых элементов 2 Nw = Nb (Nr + 1) |
| AES-128 | 128 (4) | 128 (4) | 10 | 44 |
| AES-192 | 192 (6) | 12 | 52 | |
| AES-256 | 256 (8) | 14 | 60 |
1 Слово (англ. word) – последовательность из 4 байтов (32 битов).
2 Ключевой элемент – 4-байтовое слово, формируемое из ключа.
Схемы зашифрования и расшифрования одного блока изображены на следующем рисунке.
А. Формирование ключевых элементов – KeyExpansion.
Перед процедурой зашифрования или расшифрования из ключа К формируются набор ключевых элементов wi. На следующем рисунке отображена схема формирования ключевых элементов при длине ключа Nk = 128 битов. При большей длине ключа (192 и 256 битов) имеются особенности получения wi (см. спецификацию [57]).
Рис.8.13. Cхема формирования ключевых элементов (AES-128)
Циклический сдвиг в слове wi на один байт влево.
Замена каждого байта слова wi на байт S-box в соответствии со следующей таблицей.
Таблица 8.11. S-box
(16-теричное представление)
| _0 | _1 | _2 | _3 | _4 | _5 | _6 | _7 | _8 | _9 | _A | _B | _C | _D | _E | _F | |
| 0_ | 63 | 7C | 77 | 7B | F2 | 6B | 6F | C5 | 30 | 01 | 67 | 2B | FE | D7 | AB | 76 |
| 1_ | CA | 82 | C9 | 7D | FA | 59 | 47 | F0 | AD | D4 | A2 | AF | 9C | A4 | 72 | C0 |
| 2_ | B7 | FD | 93 | 26 | 36 | 3F | F7 | CC | 34 | A5 | E5 | F1 | 71 | D8 | 31 | 15 |
| 3_ | 04 | C7 | 23 | C3 | 18 | 96 | 05 | 9A | 07 | 12 | 80 | E2 | EB | 27 | B2 | 75 |
| 4_ | 09 | 83 | 2C | 1A | 1B | 6E | 5A | A0 | 52 | 3B | D6 | B3 | 29 | E3 | 2F | 84 |
| 5_ | 53 | D1 | 00 | ED | 20 | FC | B1 | 5B | 6A | CB | BE | 39 | 4A | 4C | 58 | CF |
| 6_ | D0 | EF | AA | FB | 43 | 4D | 33 | 85 | 45 | F9 | 02 | 7F | 50 | 3C | 9F | A8 |
| 7_ | 51 | A3 | 40 | 8F | 92 | 9D | 38 | F5 | BC | B6 | DA | 21 | 10 | FF | F3 | D2 |
| 8_ | CD | 0C | 13 | EC | 5F | 97 | 44 | 17 | C4 | A7 | 7E | 3D | 64 | 5D | 19 | 73 |
| 9_ | 60 | 81 | 4F | DC | 22 | 2A | 90 | 88 | 46 | EE | B8 | 14 | DE | 5E | 0B | DB |
| A_ | E0 | 32 | 3A | 0A | 49 | 06 | 24 | 5C | C2 | D3 | AC | 62 | 91 | 95 | E4 | 79 |
| B_ | E7 | C8 | 37 | 6D | 8D | D5 | 4E | A9 | 6C | 56 | F4 | EA | 65 | 7A | AE | 08 |
| C_ | BA | 78 | 25 | 2E | 1C | A6 | B4 | C6 | E8 | DD | 74 | 1F | 4B | BD | 8B | 8A |
| D_ | 70 | 3E | B5 | 66 | 48 | 03 | F6 | 0E | 61 | 35 | 57 | B9 | 86 | C1 | 1D | 9E |
| E_ | E1 | F8 | 98 | 11 | 69 | D9 | 8E | 94 | 9B | 1E | 87 | E9 | CE | 55 | 28 | DF |
| F_ | 8C | A1 | 89 | 0D | BF | E6 | 42 | 68 | 41 | 99 | 2D | 0F | B0 | 54 | BB | 16 |
При этом байт в 16-теричном представлении состоит из двух символов, первый из которых указывает на номер строки S-box, а второй – на номер столбца. Например, если один из байтов wi = С516, то он заменяется на w’i = A616.
Иначе, таблицу S-box можно представить в виде одномерного массива. Тогда wi – это индекс элемента массива, который служит заменой – w’i = S-box[wi].
Изначально шифруемый блок T представляется массивом байтов state размером 4х4. При этом согласно спецификации AES [57] байты выписываются в массив по столбцам.
Далее над массивом state выполняются последовательные преобразования.
Сложение state по модулю 2 с четырьмя 4-байтовыми ключевыми элементами.
Замена байтов state по аналогии с SubWord в соответствии с табл.8.11.
Построчный циклический сдвиг байтов state влево на 0, 1, 2 и 3 байта.
Смешивание байтов в столбцах state. Достигается за счет умножения вектора-столбца state на квадратную матрицу mc. Умножение выполняется в поле Галуа GF(2 8 ) по модулю x 8 + x 4 + x 3 + x + 1 – обозначается жирной точкой (•).
В результате выполняется замена байтов по формулам:
Операция s • mc выполняется по правилам полиномиальной арифметики. Для этого элементы вектора и матрицы представляются в двоичном виде. Например, [s0.0, s1.0, s2.0, s3.0] = [D4, BF, 5D, 30]16 = [11010100, 10111111, 1011101, 110000]2 и [mc0.0, mc0.1, mc0.2, mc0.3] = [02, 03, 01, 01]16 = [10, 11, 01, 01]2.
Дальнейшие преобразования иллюстрируются на примере умножения и деления в столбик. Умножение выполняется классически, но со сложением единиц в столбцах по модулю 2.
| * | 11010100 10 | * | 10111111 11 |
| ⊕ | 00000000 11010100 | ⊕ | 10111111 10111111 |
| 110101000 | 111000001 |
Взятие остатка от произведения по модулю x 8 + x 4 + x 3 + x + 1 (= 1000110112) в поле Галуа GF(2 8 ) выполняется делением в столбик до тех пор, пока остаток превышает 8 битов. При этом вместо вычитания делителя из делимого также используется сложение по модулю 2.
Для s2.0 = 1 • s2.0 = 10111012 и s3.0 = 1 • s3.0 = 1100002 умножение и взятие остатка не требуется, так как их длина не превышает 8 битов. Более сложный пример деления числа C54316 = 11000101010000112 по модулю x 8 + x 4 + x 3 + x + 1 в поле Галуа GF(2 8 ) показан ниже.
| ⊕ | 1100010101000011 100011011 |
| ⊕ | 100100011 100011011 |
| ⊕ | 111000000 100011011 |
| ⊕ | 110110110 100011011 |
| ⊕ | 101011011 100011011 |
| 10000001 = 8116 |
Окончательное значение элемента s’0.0 вектора state’ получается сложением по модулю 2 полученных остатков.
При расшифровании меняется не только порядок использования ключевых элементов (как в DES и ГОСТ 28147-89), но и выполняется инверсия всех операций.
Построчный циклический сдвиг байтов state вправо на 0, 1, 2 и 3 байта.
Замена байтов state в соответствии со следующей таблицей.
Таблица 8.12. Inverse S-box
(16-теричное представление)
| _0 | _1 | _2 | _3 | _4 | _5 | _6 | _7 | _8 | _9 | _A | _B | _C | _D | _E | _F | |
| 0_ | 52 | 09 | 6A | D5 | 30 | 36 | A5 | 38 | BF | 40 | A3 | 9E | 81 | F3 | D7 | FB |
| 1_ | 7C | E3 | 39 | 82 | 9B | 2F | FF | 87 | 34 | 8E | 43 | 44 | C4 | DE | E9 | CB |
| 2_ | 54 | 7B | 94 | 32 | A6 | C2 | 23 | 3D | EE | 4C | 95 | 0B | 42 | FA | C3 | 4E |
| 3_ | 08 | 2E | A1 | 66 | 28 | D9 | 24 | B2 | 76 | 5B | A2 | 49 | 6D | 8B | D1 | 25 |
| 4_ | 72 | F8 | F6 | 64 | 86 | 68 | 98 | 16 | D4 | A4 | 5C | CC | 5D | 65 | B6 | 92 |
| 5_ | 6C | 70 | 48 | 50 | FD | ED | B9 | DA | 5E | 15 | 46 | 57 | A7 | 8D | 9D | 84 |
| 6_ | 90 | D8 | AB | 00 | 8C | BC | D3 | 0A | F7 | E4 | 58 | 05 | B8 | B3 | 45 | 06 |
| 7_ | D0 | 2C | 1E | 8F | CA | 3F | 0F | 02 | C1 | AF | BD | 03 | 01 | 13 | 8A | 6B |
| 8_ | 3A | 91 | 11 | 41 | 4F | 67 | DC | EA | 97 | F2 | CF | CE | F0 | B4 | E6 | 73 |
| 9_ | 96 | AC | 74 | 22 | E7 | AD | 35 | 85 | E2 | F9 | 37 | E8 | 1C | 75 | DF | 6E |
| A_ | 47 | F1 | 1A | 71 | 1D | 29 | C5 | 89 | 6F | B7 | 62 | 0E | AA | 18 | BE | 1B |
| B_ | FC | 56 | 3E | 4B | C6 | D2 | 79 | 20 | 9A | DB | C0 | FE | 78 | CD | 5A | F4 |
| C_ | 1F | DD | A8 | 33 | 88 | 07 | C7 | 31 | B1 | 12 | 10 | 59 | 27 | 80 | EC | 5F |
| D_ | 60 | 51 | 7F | A9 | 19 | B5 | 4A | 0D | 2D | E5 | 7A | 9F | 93 | C9 | 9C | EF |
| E_ | A0 | E0 | 3B | 4D | AE | 2A | F5 | B0 | C8 | EB | BB | 3C | 83 | 53 | 99 | 61 |
| F_ | 17 | 2B | 04 | 7E | BA | 77 | D6 | 26 | E1 | 69 | 14 | 63 | 55 | 21 | 0C | 7D |
Смешивание байтов в столбцах – умножение вектора-столбца state на квадратную матрицу mcinv с взятием остатков по модулю x 8 + x 4 + x 3 + x + 1 в поле Галуа GF(2 8 ).
Замена байтов выполняется по формулам:
В заключение несколько слов о стойкости шифра. В отличие от большинства других шифров, AES имеет простое математическое описание. Это обстоятельство беспокоит многих криптографов. Вот что по этому поводу написали известные популяризаторы криптографии Нильс Фергюсон и Брюс Шнайер.
У нас есть одно критическое замечание к AES: мы не совсем доверяем его безопасности. Что беспокоит нас больше всего в AES, так это его простая алгебраическая структура… Ни один другой блочный шифр не имеет столь простого алгебраического представления. Мы понятия не имеем, ведёт это к атаке или нет, но незнание этого является достаточной причиной, чтобы скептически относиться к использованию AES.
ГОСТ 34.12-2015 – российский стандарт симметричного блочного шифрования, введённый в действие 19 июня 2015 г. («ГОСТ 34.12-2015. Информационная технология. Криптографическая защита информации. Блочные шифры»).
Содержит описание двух блочных шифров:
— «Магма» («Magma») – с длиной блока n = 64 бит;
— «Кузнечик» («Kuznyechik») – с длиной блока n = 128 бит.
Длина ключа для обоих шифров – K = 256 бит.
Полностью соответствует ГОСТ 28147-89. В отличие от старого ГОСТ в новом явно определены значения S-блоков (подстановок π).
Таблица 8.13. Значения yij (π)
| S-блок (Sj) | Значение xij | |||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
| S1 | 12 | 4 | 6 | 2 | 10 | 5 | 11 | 9 | 14 | 8 | 13 | 7 | 0 | 3 | 15 | 1 |
| S2 | 6 | 8 | 2 | 3 | 9 | 10 | 5 | 12 | 1 | 14 | 4 | 7 | 11 | 13 | 0 | 15 |
| S3 | 11 | 3 | 5 | 8 | 2 | 15 | 10 | 13 | 14 | 1 | 7 | 4 | 12 | 9 | 6 | 0 |
| S4 | 12 | 8 | 2 | 1 | 13 | 4 | 15 | 6 | 7 | 0 | 10 | 5 | 3 | 14 | 9 | 11 |
| S5 | 7 | 15 | 5 | 10 | 8 | 1 | 6 | 13 | 0 | 9 | 3 | 14 | 11 | 4 | 2 | 12 |
| S6 | 5 | 13 | 15 | 6 | 9 | 2 | 12 | 10 | 11 | 7 | 8 | 1 | 4 | 3 | 14 | 0 |
| S7 | 8 | 14 | 2 | 5 | 6 | 9 | 1 | 12 | 15 | 4 | 11 | 0 | 13 | 10 | 3 | 7 |
| S8 | 1 | 7 | 14 | 13 | 0 | 5 | 8 | 3 | 4 | 15 | 10 | 6 | 9 | 12 | 11 | 2 |
По типу, как и AES, относится к подстановочно-перестановочным сетям. В алгоритме развертывания ключа (процедуре формирования итерационных ключей – ключевых элементов) используется сеть Фейстеля.
Схема зашифрования / расшифрования одного блока изображена на следующем рисунке.
Формирование 10 итерационных ключей (ключевых элементов) выполняется по следующей схеме.
Рис.8.15. Развертывание K
Изначально ключ делится на две половины по 128 битов с получение первых двух итерационных ключей (k1 и k2).
Далее, в течение 4 раундов i, формируются остальные 8 итерационных ключей (k2i+1 и k2i+2). Каждая последующая пара итерационных ключей получается в результате прогона предыдущей пары через сеть, состоящую из 8 ячеек Фейстеля (в ГОСТ ячейка обозначена F). При этом в начале каждой итерации j (ячейки F) должна быть получена итерационная константа С8(i-1)+j (не путать с обозначением блока шифрограммы С на рис.8.14). Для этого целое число 8(i-1)+j, представленное в двоичном виде на 128 битов, должно пройти преобразование L.
A.1. Линейное преобразование L.
Преобразование байтов ai входного 128-битового (16-байтового) массива V в течение 16 раундов по следующей схеме.
Рис.8.16. Линейное преобразование L
Один раунд состоит из следующей последовательности операций:
— умножение (•) каждого байта ai массива V на соответствующую константу, определенную в ГОСТ;
— сложение по модулю 2 результатов умножения (a ⊕ );
— сдвиг вправо элементов массива V на 1 байт;
— занесение a ⊕ в качестве первого (старшего) байта массива V.
Массив констант по ГОСТ представлен в следующей таблице.
Таблица 8.14. Массив констант
| № п/п | Основание системы счисления | ||
| 16 | 10 | 2 | |
| 1 | 94 | 148 | 10010100 |
| 2 | 20 | 32 | 00100000 |
| 3 | 85 | 133 | 10000101 |
| 4 | 10 | 16 | 00010000 |
| 5 | C2 | 194 | 11000010 |
| 6 | C0 | 192 | 11000000 |
| 7 | 01 | 1 | 00000001 |
| 8 | FB | 251 | 11111011 |
| 9 | 01 | 1 | 00000001 |
| 10 | C0 | 192 | 11000000 |
| 11 | C2 | 194 | 11000010 |
| 12 | 10 | 16 | 00010000 |
| 13 | 85 | 133 | 10000101 |
| 14 | 20 | 32 | 00100000 |
| 15 | 84 | 148 | 10010100 |
| 16 | 01 | 1 | 00000001 |
Проиллюстрируем выполнение операций на примере 4 раунда определения итерационной константы C1 (см. п.A.1.4 приложения А к ГОСТ 34.12-2015).
Массив V в начале итерации – [84, 94, 01, 00, 00, …, 00]16 = [10000100, 10010100, 00000001, 00000000, 00000000, …, 00000000]2.
Умножение (•) байта на константу выполняется в поле Галуа GF(2 8 ) по модулю x 8 + x 7 + x 6 + x + 1 (=1110000112 = 1C316) в соответствии с правилами полиномиальной арифметики (см. функцию MixColumns шифра AES):
| 84 * 94 | 94 * 20 | 01 * 85 | |||
| * | 10000100 10010100 | * | 10010100 00100000 | * | 00000001 10000101 |
| ⊕ | 00000000 00000000 10000100 00000000 10000100 00000000 00000000 10000100 | ⊕ | 00000000 00000000 00000000 00000000 00000000 10010100 00000000 00000000 | ⊕ | 00000001 00000000 00000001 00000000 00000000 00000000 00000000 00000001 |
| 100100001010000 = 485016 | 001001010000000 = 128016 | 000000010000101 = 8516 |
— полиномиальное деление (для 8516 не требуется, т.к. число не превышает 8 битов):
| 4850 mod 1C3 | 1280 mod 1C3 | ||
| ⊕ | 100100001010000 111000011 | ⊕ | 1001010000000 111000011 |
| ⊕ | 111000100 111000011 | ⊕ | 111010110 111000011 |
| 11110000 = F016 | 10101000 = A816 |
Сдвиг массива V вправо – [ _, 84, 94, 01, 00, …, 00]16.
Занесение a ⊕ в качестве первого (старшего) байта массива V – [DD, 84, 94, 01, 00, …, 00]16.
A.2. Нелинейное биективное преобразование S.
Замена каждого байта ai входного 128-битового (16-байтового) массива V на байт подстановки π в соответствии со следующей таблицей.
Таблица 8.15. Подстановки π
(16-теричное представление)
| _0 | _1 | _2 | _3 | _4 | _5 | _6 | _7 | _8 | _9 | _A | _B | _C | _D | _E | _F | |
| 0_ | FC | EE | DD | 11 | CF | 6E | 31 | 16 | FB | C4 | FA | DA | 23 | C5 | 04 | 4D |
| 1_ | E9 | 77 | F0 | DB | 93 | 2E | 99 | BA | 17 | 36 | F1 | BB | 14 | CD | 5F | C1 |
| 2_ | F9 | 18 | 65 | 5A | E2 | 5C | EF | 21 | 81 | 1C | 3C | 42 | 8B | 01 | 8E | 4F |
| 3_ | 05 | 84 | 02 | AE | E3 | 6A | 8F | A0 | 06 | 0B | ED | 98 | 7F | D4 | D3 | 1F |
| 4_ | EB | 34 | 2C | 51 | EA | C8 | 48 | AB | F2 | 2A | 68 | A2 | FD | 3A | CE | CC |
| 5_ | B5 | 70 | 0E | 56 | 08 | 0C | 76 | 12 | BF | 72 | 13 | 47 | 9C | B7 | 5D | 87 |
| 6_ | 15 | A1 | 96 | 29 | 10 | 7B | 9A | C7 | F3 | 91 | 78 | 6F | 9D | 9E | B2 | B1 |
| 7_ | 32 | 75 | 19 | 3D | FF | 35 | 8A | 7E | 6D | 54 | C6 | 80 | C3 | BD | 0D | 57 |
| 8_ | DF | F5 | 24 | A9 | 3E | A8 | 43 | C9 | D7 | 79 | D6 | F6 | 7C | 22 | B9 | 03 |
| 9_ | E0 | 0F | EC | DE | 7A | 94 | B0 | BC | DC | E8 | 28 | 50 | 4E | 33 | 0A | 4A |
| A_ | A7 | 97 | 60 | 73 | 1E | 00 | 62 | 44 | 1A | B8 | 38 | 82 | 64 | 9F | 26 | 41 |
| B_ | AD | 45 | 46 | 92 | 27 | 5E | 55 | 2F | 8C | A3 | A5 | 7D | 69 | D5 | 95 | 3B |
| C_ | 07 | 58 | B3 | 40 | 86 | AC | 1D | F7 | 30 | 37 | 6B | E4 | 88 | D9 | E7 | 89 |
| D_ | E1 | 1B | 83 | 49 | 4C | 3F | F8 | FE | 8D | 53 | AA | 90 | CA | D8 | 85 | 61 |
| E_ | 20 | 71 | 67 | A4 | 2D | 2B | 09 | 5B | CB | 9B | 25 | D0 | BE | E5 | 6C | 52 |
| F_ | 59 | A6 | 74 | D2 | E6 | F4 | B4 | C0 | D1 | 66 | AF | C2 | 39 | 4B | 63 | B6 |
При этом байт ai в 16-теричном представлении состоит из двух символов, первый из которых указывает на номер строки подстановки π, а второй – на номер столбца. Например, если один из байтов ai = С516, то он заменяется на a’i = AC16.
Иначе, таблицу подстановок π можно представить в виде одномерного массива. Тогда ai – это индекс элемента массива, который служит заменой – a’i = π[ai].
Зашифрование представляет собой последовательное применение к исходному блоку текста Т в течение 9 раундов r гаммирования по модулю 2 с итерационными ключами kr, а также преобразований S и L (см. A.1 и A.2). Для окончательного получения блока шифрограммы С результат раундовых преобразований складывается по модулю 2 с последним итерационным ключом k10.
При расшифровании меняется не только порядок использования итерационных ключей (как в DES и ГОСТ 28147-89), но и выполняется инверсия всех операций.
Преобразование байтов ai входного 128-битового (16-байтового) массива V в течение 16 раундов по следующей схеме.
— сдвиг выполняется в начале итерации;
— используется циклический сдвиг влево вместо простого сдвига вправо;
— результат сложения a ⊕ заносится как последний (младший) байт массива V.
| _0 | _1 | _2 | _3 | _4 | _5 | _6 | _7 | _8 | _9 | _A | _B | _C | _D | _E | _F | |
| 0_ | A5 | 2D | 32 | 8F | 0E | 30 | 38 | C0 | 54 | E6 | 9E | 39 | 55 | 7E | 52 | 91 |
| 1_ | 64 | 03 | 57 | 5A | 1C | 60 | 07 | 18 | 21 | 72 | A8 | D1 | 29 | C6 | A4 | 3F |
| 2_ | E0 | 27 | 8D | 0C | 82 | EA | AE | B4 | 9A | 63 | 49 | E5 | 42 | E4 | 15 | B7 |
| 3_ | C8 | 06 | 70 | 9D | 41 | 75 | 19 | C9 | AA | FC | 4D | BF | 2A | 73 | 84 | D5 |
| 4_ | C3 | AF | 2B | 86 | A7 | B1 | B2 | 5B | 46 | D3 | 9F | FD | D4 | 0F | 9C | 2F |
| 5_ | 9B | 43 | EF | D9 | 79 | B6 | 53 | 7F | C1 | F0 | 23 | E7 | 25 | 5E | B5 | 1E |
| 6_ | A2 | DF | A6 | FE | AC | 22 | F9 | E2 | 4A | BC | 35 | CA | EE | 78 | 05 | 6B |
| 7_ | 51 | E1 | 59 | A3 | F2 | 71 | 56 | 11 | 6A | 89 | 94 | 65 | 8C | BB | 77 | 3C |
| 8_ | 7B | 28 | AB | D2 | 31 | DE | C4 | 5F | CC | CF | 76 | 2C | B8 | D8 | 2E | 36 |
| 9_ | DB | 69 | B3 | 14 | 95 | BE | 62 | A1 | 3B | 16 | 66 | E9 | 5C | 6C | 6D | AD |
| A_ | 37 | 61 | 4B | B9 | E3 | BA | F1 | A0 | 85 | 83 | DA | 47 | C5 | B0 | 33 | FA |
| B_ | 96 | 6F | 6E | C2 | F6 | 50 | FF | 5D | A9 | 8E | 17 | 1B | 97 | 7D | EC | 58 |
| C_ | F7 | 1F | FB | 7C | 09 | 0D | 7A | 67 | 45 | 87 | DC | E8 | 4F | 1D | 4E | 04 |
| D_ | EB | F8 | F3 | 3E | 3D | BD | 8A | 88 | DD | CD | 0B | 13 | 98 | 02 | 93 | 80 |
| E_ | 90 | D0 | 24 | 34 | CB | ED | F4 | CE | 99 | 10 | 44 | 40 | 92 | 3A | 01 | 26 |
| F_ | 12 | 1A | 48 | 68 | F5 | 81 | 8B | C7 | D6 | 20 | 0A | 08 | 00 | 4C | D7 | 74 |
Является дополнением к ГОСТ 34.12-2015 и определяет режимы работы блочных шифров:
— простой замены (Electronic Codebook, ЕСВ);
— гаммирования (Counter, CTR);
— гаммирования с обратной связью по выходу (Output Feedback, OFB);
— простой замены с зацеплением (Cipher Block Chaining, СВС);
— гаммирования с обратной связью по шифртексту (Cipher Feedback, CFB);
— выработки имитовставки (Message Authentication Code algorithm).
Для каждого из режимов в стандарте приведены схемы зашифрования / расшифрования, которые в качестве базовых операций используют процедуры зашифрования / расшифрования по ГОСТ 34.12-2015.