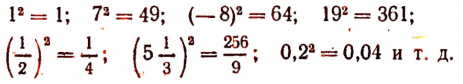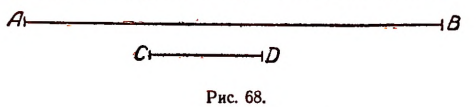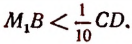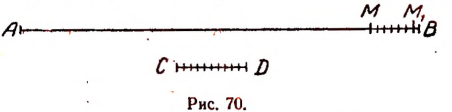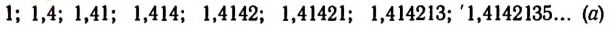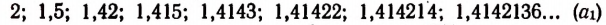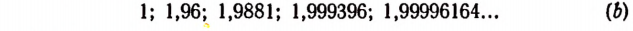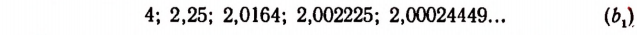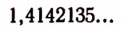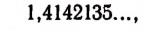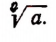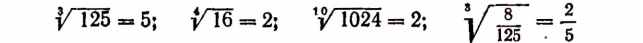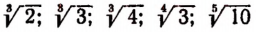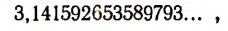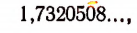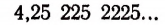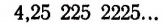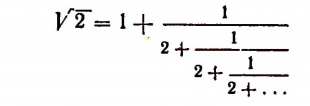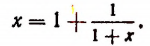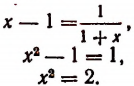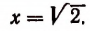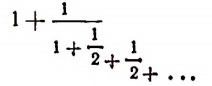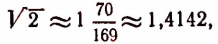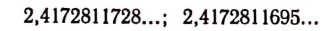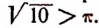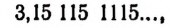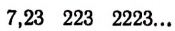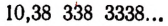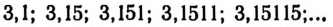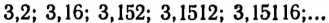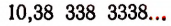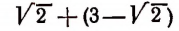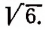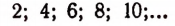в чем смысл иррациональных чисел

В чем смысл иррациональных чисел

Множество иррациональных чисел обычно обозначается заглавной латинской буквой в полужирном начертании без заливки. Таким образом: , т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.

О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа .

Свойства

Примеры

Примеры доказательства иррациональности

Корень из 2

Допустим противное: рационален, то есть представляется в виде несократимой дроби , где — целое число, а — натуральное число. Возведём предполагаемое равенство в квадрат:

.

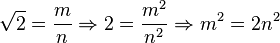
Отсюда следует, что 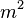чётно, значит, чётно и . Пускай , где целое. Тогда

Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.

Двоичный логарифм числа 3

Допустим противное: рационален, то есть представляется в виде дроби , где и — целые числа. Поскольку 0″ src=»http://upload.wikimedia.org/math/d/1/3/d1351d4222403731e31419faebbe54bc.png» />, и могут быть выбраны положительными. Тогда

Но чётно, а нечётно. Получаем противоречие.

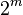
История

Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. — ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.

Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок. 500 гг. до н. э.), пифагорейцу, который нашёл это доказательство, изучая длины сторон пентаграммы. Во времена пифагорейцев считалось, что существует единая единица длины, достаточно малая и неделимая, которая целое число раз входит в любой отрезок. Однако Гиппас обосновал, что не существует единой единицы длины, поскольку предположение о её существовании приводит к противоречию. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным. Доказательство выглядело следующим образом:

Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.

Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному предположению Жана Итара (1961), оно было основано на пифагорейской теории чётных и нечётных чисел, в том числе — на теореме о том, что нечётное квадратное число за вычетом единицы делится на восемь треугольных чисел.

Позже Евдокс Книдский (410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию пропорций, которая принимала во внимание как рациональные, так и иррациональные отношения. Это послужило основанием для понимания фундаментальной сути иррациональных чисел. Величина стала считаться не числом, но обозначением сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени — сущностей, которые могут меняться непрерывно (в современном понимании этого слова). Величины были противопоставлены числам, которые могут меняться лишь «прыжками» от одного числа к соседнему, например, с 4 на 5. Числа составляются из наименьшей неделимой величины, в то время как величины можно уменьшать бесконечно.

Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами. «Книга 10 Элементов» Евклида посвящена классификации иррациональных величин.

Средние века

Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сперва индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.

Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 Элементов Евклида, персидский математик Аль Махани (ок 800 гг. н. э.) исследовал и классифицировал квадратичные иррациональные числа (числа вида) и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например:

Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких так 10, 15, 20 — не являющихся квадратами.

В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин:

результат сложения иррациональной величины и рациональной, результат вычитания рациональной величины из иррациональной, результат вычитания иррациональной величины из рациональной.

Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени. В X веке иракский математик Аль Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами. Ал Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины:

Пусть единична величина содержится в данной величине один или несколько раз, тогда эта [данная] величина соответствует целому числу… Каждая величина, которая составляет половину, или треть, или четверть единичной величины, или, сравненная с единичной величиной составляет три пятых от нее, это рациональная величина. И в целом, всякая величина, которая относится к единичной как одно число к другому, является рациональной. Если же величина не может быть представлена как несколько или часть (l/n), или несколько частей (m/n) единичной длины, она иррациональная, то есть невыразимая иначе как с помощью корней.

Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввел современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к π, а также показали иррациональность некоторых тригонометрических функций. Джестадева привел эти результаты в книге Йуктибхаза.

Наше время

В XVII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер (1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с Гейне, именно 1872 год принято считать годом рождения теории. Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемым) Дедекиндовым сечением множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.

Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей.

Источник

Иррациональные числа в математике и их свойства с примерами решения и образцами выполнения

На первый взгляд может показаться, что никаких других чисел, кроме рациональных, и быть не может. В действительности же это не так. Мы увидим, что, кроме рациональных чисел, существуют и другие.

Станем исходить из того, что нам известны лишь рациональные числа и никакие другие. Тогда действие возведения в квадрат иад этими числами окажется выполнимым всегда.

Между тем действие извлечения квадратного корня выполнимо уже далеко не всегда.

Например, действие извлечения квадратного корня из двух окажется невыполнимым, так как во множестве рациональных чисел нет такого числа, квадрат которого был бы равен двум (см. стр. 244).

Таким образом, чтобы сделать возможным выполнение действия извлечения арифметического квадратного корня, во всех случаях снова требуется прибегнуть к дальнейшему расширению нашего понятия о числе.

Здесь мы снова видим, что для выполнения прямого действия (возведения в квадрат) не требовалось расширять рациональную числовую область, а для безотказного выполнения обратного действия (извлечения квадратного корня) такое расширение уже становится необходимым.

К расширению области рациональных чисел нас приводит и рассмотрение вопроса об отношении несоизмеримых отрезков (см. стр. 247).

Действительно, оставаясь в области рациональных чисел, мы не можем выразить точно отношение несоизмеримых отрезков, а следовательно, и длину отрезка, несоизмеримого с единицей длины (см. стр. 248).

Таким образом, к расширению рациональной числовой области приводят нас потребности не только алгебры, но и геометрии.

Существование на числовой оси точек, не являющихся рациональными

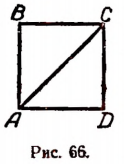
Было доказано, что диагональ и сторона квадрата несоизмеримы (см. стр. 246). Отсюда вытекает следующее: если длину стороны квадрата принять за единицу, то не будет существовать никакого рационального числа, которое выражало бы точно длину диагонали.

Пусть ABCD (рис. 66) есть квадрат, сторона которого принята за единицу длины.

Отложим на числовой оси (рис. 67) отрезки ОМ и равные диагонали АС. Тогда точки М и не будут рациональными («черными») точками числовой оси, а следовательно, будут точками, которые мы назвали образно «красными».

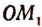
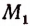
Но так как отрезков, несоизмеримых с единицей; длины, существует бесконечное множество то и точек на числовой оси, не являющихся рациональными, также существует бесконечное множество.

Выше мы назвали образно все рациональные точки числовой оси «черными», а все остальные «красными». Отсюда следует, что «черные» и «красные» точки заполняют собой всю числовую ось сплошь. Иначе говоря, на числовой оси, кроме рациональных («черных») и нерациональных («красных») точек, никаких других точек нет.

В § 5, гл. XVII было доказано, что между двумя любыми различными рациональными («черными») точками существует бесконечное множество других рациональных («черных») точек. В связи с этим примем к сведению без доказательства следующее: на любом сколь угодно малом отрезке числовой, оси, где бы он ни был расположен, имеется бесконечное множество рациональных („черных») и бесконечное множество „красных» точек.

При этом оказывается, что бесконечное множество нерациональных (т. е. «красных») точек числовой оси существенно «богаче» множества ее рациональных (т. е. «черных») точек. Это же самое в точных терминах можно сформулировать так: множество нерациональных (т. е. «красных») точек числовой оси имеет мощность (см. §6 этой же главы) более высокую, чем мощность множества рациональных (т. е. «черных») точек.

Выражаясь образно, можно сказать, что числовая ось настолько сильно насыщена «красными» (т. е. нерациональными) точками, что вся она, по нашей условной терминологии, представлялась бы нам как бы сплошь красной.

Понятие об иррациональном числе

1. Мы убедились в том, что одних рациональных чисел недостаточно для потребностей алгебры и геометрии.

Мы видели, что нет такого рационального числа, которое равнялось бы точно . (Аналогично можно было бы убедиться, что нет таких рациональных чисел, которые равнялись бы точно, например, и многим другим квадратным корням.) Мы знаем еще и то, что существуют отрезки, точное отношение которых не выражается никаким рациональным числом (см. стр. 247). Мы также знаем, что на числовой оси существуют такие точки, точные расстояния которых от начальной точки числовой оси не выражаются никакими рациональными числами (см. стр. 254). Значит, для изображения этих величин необходимы какие-то новые числа.

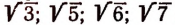
Как же составить представление об этих новых числах.

Во-первых, заметим, что такими новыми числами никак не могут быть ни конечные десятичные дроби, ни бесконечные периодические десятичные дроби, так как те и другие являются числами рациональными (см. стр. 251).

Во-вторых, заметим, что никакая бесконечная непериодическая дробь не может изображать собой рациональное число, так как всякое рациональное число (как известно из арифметики), будучи изображенным в форме бесконечной дроби, дает дробь обязательно периодическую.

Чтобы составить себе представление об этих новых числах, рассмотрим еще раз вопрос об измерении отрезка, несоизмеримого с единицей длины, и вопрос о квадратном корне из двух.

Пусть отрезки АВ и CD (рис. 68)

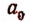
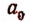
Первый шаг. Примем отрезок CD за единицу измерения и станем откладывать его последовательно на отрезке АВ. Пусть отрезок CD отложился раз и получился остаток MB, меньший CD. (На рис. 69 = 5.) Эту операцию назовем первым шагом.

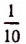
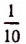
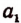
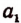
Второй шаг. Разделим отрезок CD на десять равных частей и будем откладывать часть CD на остатке MB. Пусть часть CD отложилась на MB раз (на рис. 70 = 6).

Тогда обязательно получится второй остаток

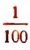
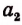
Третий шаг. На втором остатке откладываем часть CD. Получим целое число и третий остаток

Этот процесс мы продолжаем дальше, делая четвертый, пятый и дальнейшие шаги.

В силу несоизмеримости отрезков АВ и CD этот процесс теоретически никогда не кончится и длина АВ выразится бесконечной десятичной дробью. Эта бесконечная десятичная дробь не будет периодической, так как в таком случае отрезки АВ и CD оказались бы соизмеримыми, тогда как по условию они несоизмеримы.

Вот эта бесконечная непериодическая десятичная дробь и будет примером нового числа, не являющегося рациональным и называемого иррациональным. Этим числом и будет выражаться длина отрезка АВ.

Определение:

Иррациональным числом называется бесконечная непериодическая десятичная (положительная или отрицательная) дробь.

Например, бесконечная непериодическая дробь

8,121121112…

есть вполне определенное иррациональное число.

Ниже будет показано, что математическое выражение, например есть также определенное иррациональное число.

Мы уже умеем находить приближенные значения с любой сколь угодно высокой степенью точности, т. е. мы можем находить сколько угодно десятичных знаков, идущих после запятой в десятичной дроби, которая изображает приближенное значение .

При этом нам ясно, что процесс извлечения никогда не может закончиться. Если бы этот процесс мог закончиться, то был бы равен некоторой дроби , что невозможно.

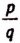
Нам также ясно, что в результате бесконечного процесса извлечения не может получиться периодическая бесконечная дробь. Если бы получилась периодическая бесконечная дробь, то это означало бы опять, что равен некоторой дроби , что невозможно. (Ведь периодическая бесконечная дробь есть число рациональное.)

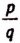
Бесконечный ряд чисел

представляет собой приближенные значения с недостатком, с точностью до и т. д.

Бесконечный же ряд чисел

представляет собой приближенные значения с избытком, с точностью до и т. д.

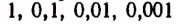
Квадратами чисел ряда (а) будут

Квадратами чисел ряда (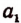) будут

Числа, записанные в рядах (b) и , становятся тем ближе к числу 2, чем больше десятичных знаков мы берем.

Ряд (а) обладает той особенностью, что раз полученный десятичный знак навсегда сохраняется при продолжении процесса.

Это, естественно, приводит к мысли принять за бесконечную десятичную дробь

Но эта бесконечная дробь не может оказаться периодической, как это уже было доказано выше.

Итак, квадратный корень из двух изображается бесконечной непериодической десятичной дробью. Следовательно, есть число иррациональное.

Написать бесконечную непериодическую десятичную дробь, разумеется, нельзя. Мы, однако, считаем ее определенной, если имеется то или иное правило, позволяющее написать любой его десятичный знак, как бы далеко ни стоял этот знак в последовательности десятичных знаков.

Например, тысячный знак в бесконечной десятичной дроби

изображающей иррациональное число имеет вполне определенную величину, несмотря на то, что его едва ли кто знает. Впрочем, при помощи современных электронных цифровых вычислительных машин найти этот тысячный знак можно довольно быстро.

Аналогично тому, как мы доказали, что есть число иррациональное, можно доказать, что числа и т. д. также являются иррациональными.

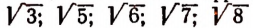
Чтобы показать существование других иррациональных чисел, введем понятие арифметического корня n-й степени.

Определение:

Арифметическим корнем n-й степени из положительного числа а называется такое новое положительное число, п-я степень которого равна а.

Корень n-й степени из а обозначается символом

Примеры:

Корни 3-й степени называют кубическими корнями. Например, 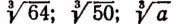суть кубические корни.

Примем к сведению без доказательства, что, например,

и им подобные представляют собой числа иррациональные.

Но ошибочно было бы думать, что иррациональные числа порождаются только корнями. Наоборот, существует много других источников, порождающих иррациональные числа. Например, мы видели, что длина всякого отрезка, несоизмеримого с единицей длины, есть число иррациональное, независимо от того, может или не может эта длина выражаться точно с помощью одного или нескольких корней.

Доказано, что отношение длины окружности к своему диаметру есть число иррациональное. Доказано, кроме того, что это иррациональное число не может быть точно представлено с помощью одного или нескольких корней.

Отношение длины окружности к своему диаметру принято обозначать греческой буквой 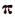(«пи»).

Иррациональность числа 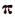впервые была доказана немецким математиком Ламбертом в 1766 году.

Число 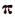изображается бесконечной непериодической дробью

первые 15 десятичных знаков которой здесь выписаны.

Число 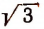изображается бесконечной непериодической дробью

первые 7 десятичных знаков которой здесь выписаны.

Мы уже знаем, что любая бесконечная непериодическая десятичная дробь представляет собой число иррациональное.

Теперь может возникнуть вопрос о том, как же понимать смысл самой бесконечной непериодической десятичной дроби.

Возьмем какую-нибудь бесконечную непериодическую десятичную дробь, например 4,25 225 2225… Составим две последовательности чисел.

Первая последовательность: 4,2; 4,25; 4,252; 4,2522; 4,25225…

Вторая последовательность: 4,3; 4,26; 4,253; 4,2523, 4,25226…

Доказано (доказательства мы здесь не приводим), что этими двумя бесконечными последовательностями определяется единственное число, которое больше каждого числа первой последовательности и меньше каждого числа второй последовательности. Это единственное число мы и понимаем под символом

Таким образом, конкретное представление об иррациональном числе

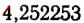
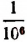
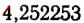
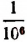
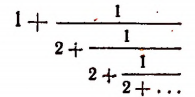
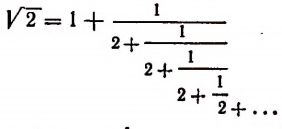
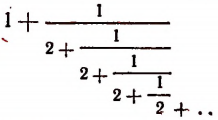
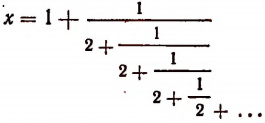
мы можем себе составить путем рассмотрения указанных выше двух бесконечных последовательностей. Эти две бесконечные последовательности дают возможность находить приближенные значения определяемого ими иррационального числа с любой точностью— с недостатком и с избытком. Например, число есть приближенное значение с недостатком с точностью до . Число же есть приближенное значение с избытком с точностью до .

Мы уже убедились в том, что всякая бесконечная десятичная непериодическая дробь является числом иррациональным. Однако существуют и другие бесконечные процессы, определяющие собой то или иное иррациональное число. Например, бесконечный процесс

определяет собой иррациональные числа , так что

Пояснения к формуле

представляет собой некоторый, идущий по определенному закону, бесконечный процесс. Если допустить, что этот бесконечный процесс определяет собой некоторое число то получим

Перепишем эту формулу в следующем виде:

Выражение в предыдущей формуле, отмеченное одной фигурной скобкой, представляет тот же самый бесконечный процесс, которым (как мы допустили) определяется число х. Поэтому получим, что

Из этого уравнения следует, что

Но так как х — число положительное, то

Итак, доказано следующее. Если допустить, что бесконечным процессом

определяется некоторое число, то этим числом будет как раз иррациональное число .

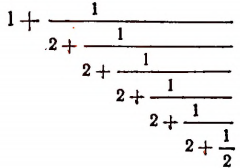
Примем к сведению без доказательства, что, беря все большее и большее число звеньев этого бесконечного процесса, мы можем получать рациональные приближения иррационального числа 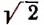все с большей и большей точностью.

Например, значение выражения

равно 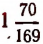. Отсюда

что как раз и представляет приближенное значение 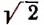с недостатком с точностью до 0,0001.

Сравнение иррациональных чисел

Два иррациональных числа называются равными, если их изображения с помощью бесконечных непериодических десятичных дробей одинаковы (тождественны).

Из двух положительных иррациональных чисел больше то, у которого целая часть больше. Если же целые части равны, то большим будет то, у которого больше первый десятичный знак после запятой. Если же и первые десятичные знаки одинаковы, то большим будет то, у которого больше второй десятичный знак и т. д.

Например, сравним следующие иррациональные числа:

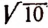
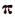
Здесь одинаковы целые части; первые семь десятичных знаков во втором числе такие же, как и в первом. Восьмой десятичный знак первого числа больше восьмого десятичного знака второго числа. Поэтому первое иррациональное число больше второго. Выписав достаточное число десятичных знаков бесконечных непериодических десятичных дробей изображающих иррациональные числа и , убедитесь, что

Сложение и умножение иррациональных чисел

Поясним, что такое сумма двух иррациональных чисел. Пусть иррациональное число а изображается следующей бесконечной непериодической десятичной дробью

а иррациональное число b — дробью

Тогда сумма а + b изобразится дробью

Эта дробь бесконечная, непериодическая, десятичная; значит, она изображает собой определенное иррациональное число.

Напишем последовательности чисел, изображающих приближенные значения числа а:

с недостатком:
с избытком:

Сделаем то же самое и для числа b:

Составим еще две следующие последовательности:

В последовательности (I) идут суммы соответствующих приближенных значений чисел a и b с недостатком, ав(II)с избытком.

Под суммой а + b подразумевается такое число, которое больше каждого члена бесконечной последовательности (I) и меньше каждого члена бесконечной последовательности (II).

Таким числом как раз будет дробь

Определение:

Суммой двух положительных иррациональных чисел называется число, которое больше суммы любых их приближенных значений с недостатком, но меньше суммы любых их приближенных значений с избытком. Такое число, как это доказано в строгой теории иррациональных чисел, всегда существует и притом только одно.

Сумма двух иррациональных чисел, вообще говоря, будет числом иррациональным, но может оказаться и рациональным.

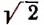
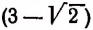
Например, числа и оба иррациональные, между тем как их сумма

есть рациональное число 3.

Определение:

Произведением двух положительных иррациональных чисел называется число, которое больше произведений любых их приближенных значений с недостатком, но меньше произведений любых их приближенных значений с избытком.

Такое число также всегда существует и притом только одно.

Произведение двух иррациональных чисел, вообще говоря, будет числом иррациональным, но может оказаться и рациональным.

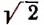
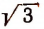
Например, произведение иррациональных чисел и будет иррациональным числом, равным

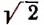
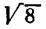
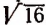
Произведение же иррациональных чисел и будет равно , т. е. рациональному числу 4.

По аналогии с приведенными рассуждениями читатель сможет сам составить определения сложения и умножения двух чисел для того случая, когда одно из них рациональное, а другое иррациональное.

Подобно этому определяется вычитание и деление иррациональных чисел.

Понятие действительного числа

Определение:

Все рациональные и иррациональные числа, как положительные, так и отрицательные, называются действительными, или вещественными, числами.

Примем к сведению без доказательства, что особенности нуля и единицы (см. стр. 41), а также переместительный и сочетательный законы сложения и переместительный сочетательный и распределительный законы умножения (см. стр. 32 и 39) остаются в силе для всех действительных чисел (рациональных и иррациональных).

Примеры для закрепления терминологии

Слово «рациональный» происходит от латинского слова «rationalis», что означает — «разумный», «обоснованный».

Слово «иррациональный» происходит также от латинского слова «irratlonalis», что означает — «неразумный», «необоснованный».

Можно было бы подумать, что числа, несоизмеримые с единицей, были названы «иррациональными» потому, что их действительно считали не поддающимися логическому пониманию. На самом деле это не так. Еще у древнегреческого математика Евклида встречаются такие определения, из которых видно, что он отнюдь не считал «иррациональные числа» «неразумными», «нелогичными».

Строгая теория иррациональных чисел была построена впервые лишь во второй половине XIX века немецким математиком Дедекиндом. Со строгой теорией иррациональных чисел можно ознакомиться, например, по книге А. Н. Колмогорова и П. С. Александрова «Введение в теорию функций действительного переменного».

Примечание:

Примем к сведению без доказательства, что правила и формулы, выведенные для рациональных чисел, остаются в силе и для всех действительных чисел. Например, правила умножения и деления степеней, формулы умножения, свойства пропорций, свойство ряда равных отношений и т. д.

Некоторые понятия и предложения элементарной теории множеств

О бесконечных множествах

В математике постоянно приходится иметь дело с бесконечными множествами.

Приведем несколько примеров таких множеств:

1) множество всех натуральных чисел;
2) множество всех четных чисел;
3) множество всех простых чисел;
4) множество всех, рациональных чисел;
5) множество всех иррациональных чисел;
6) множество всех действительных чисел;
7) множество всех различных прямоугольных треугольников с гипотенузой, равной единице;
8) множество всех различных квадратных уравнений с действительными числовыми коэффициентами.

Введем понятие о взаимно однозначном соответствии.

Мы уже знаем, что каждому действительному числу соответствует определенная точка числовой оси и, наоборот, каждой точке числовой оси соответствует определенное действительное число. Имея это в виду, говорят, что между множеством действительных чисел и множеством точек числовой оси имеет место взаимно однозначное соответствие.

Приведем другой пример взаимно однозначного соответствия.

Между множеством всех целых положительных чисел и множеством целых отрицательных чисел можно установить взаимно однозначное соответствие. Например, каждому целому положительному числу можно поставить в соответствие число, ему противоположное.

Определение:

Если между элементами двух множеств можно установить взаимно однозначное соответствие, то такие два множества называются эквивалентными.

Пример:

Множество точек числовой оси и множество действительных чисел эквивалентны. Каждой точке числовой оси соответствует одно и только одно определенное действительное число и, наоборот, каждому действительному числу соответствует одна и только одна определенная точка числовой оси.

Пример:

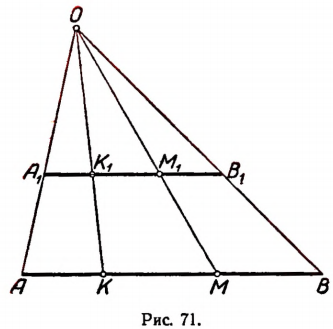
Множество точек отрезка АВ (рис. 71) и множество точек отрезка 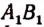— эквивалентны.

Каждой точке М отрезка А В можно поставить в соответствие одну и только одну точку отрезка лежащую на луче ОМ. Наоборот, каждой точке отрезка можно поставить в соответствие одну и только одну точку К отрезка АВ, лежащую на луче ОК.

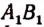
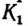
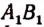
Пример:

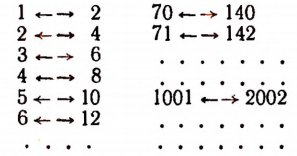
Множество всех целых положительных чисел

эквивалентно множеству всех положительных четных чисел

В самом деле, мы можем поставить в соответствие каждому целому числу число, вдвое большее его. Наоборот, каждому четному числу мы можем поставить в соответствие число, вдвое меньшее его.

Взаимно однозначное соответствие между рассмотренными множествами (пример 3) мы можем записать в виде следующей таблицы:

Относительно двух эквивалентных бесконечных множеств говорят также, что они имеют одинаковую мощность. Другими словами, два бесконечных множества имеют одинаковую мощность, если эти множества эквивалентны.

Счетные множества и множества мощности континуума

Множество, эквивалентное множеству всех целых положительных чисел, называется счетным множеством. Например, множество всех положительных четных чисел есть счетное множество. Множество всех положительных нечетных чисел также будет счетным, так как оно тоже эквивалентно множеству всех целых положительных чисел.

Так как всякое множество эквивалентно самому себе, то и множество целых положительных чисел также является счетным множеством.

Множество, эквивалентное множеству всех действительных чисел, называется множеством мощности континуума.

Множество точек числовой оси эквивалентно множеству действительных чисел. Поэтому множество точек числовой оси также имеет мощность континуума.

Приведем еще примеры множеств, имеющих мощность континуума.

Пример:

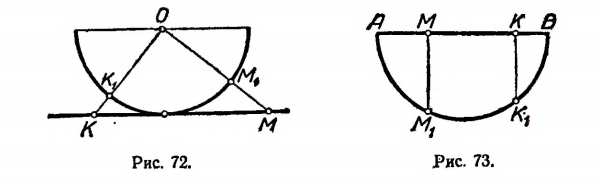
Множество точек полуокружности имеет мощность континуума. В самом деле, легко убедиться в том, что множество точек полуокружности эквивалентно множеству точек числовой оси. Каждой точке полуокружности (рис. 72) можно поставить в соответствие одну и только одну точку М числовой оси, лежащую на луче . Наоборот, каждой точке К числовой оси можно поставить в соответствие одну и только одну точку полуокружности, лежащую на луче ОК.

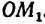
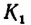
Пример:

Множество точек любого отрезка прямой имеет мощность континуума.

Доказательство:

Множество точек отрезка прямой эквивалентно множеству точек полуокружности, построенной на этом отрезке как на диаметре.

В самом деле, каждой точке М отрезка АВ (рис. 73) можно поставить в соответствие одну и только одну определенную точку полуокружности, лежащую на перпендикуляре к прямой АВ, восставленном из точки М. Далее, каждой точке полуокружности можем поставить в соответствие одну и только одну точку К отрезка АВ, лежащую на перпендикуляре, опущенном из точки на прямую АВ.

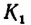
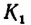
Но ранее было доказано, что множество точек полуокружности имеет мощность континуума. Следовательно, и мощность множества точек любого отрезка прямой также ийеет мощность континуума, что и требовалось доказать.

Так как всякое множество эквивалентно самому себе, то множество действительных чисел также имеет мощность континуума.

Примем к сведению без доказательства следующее.

С теорией множеств можно ознакомиться, например, по книге А. Н. Колмогорова и С. Ф. Фомина «Элементы теории функций и функционального анализа».

Дополнение к иррациональным числам

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник