в чем сходство между математической и естественнонаучной грамотностью
Тема: «Справочный материал о международных исследованиях, связанных с оценкой математической грамотности».
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Курсы повышения квалификации учителей математики
« Развитие функциональной математической грамотности учащихся в рамках проведения международного исследования PISA » 04.08-15.08.2014 г.
Тема: «Справочный материал о международных исследованиях, связанных с оценкой
Выполнил: учитель математики
1. Цели и задачи исследований……. ………………………………….…………..3
2. Понятие математической грамотности в исследованиях …….………………..4
3.Оценка уровня математической грамотности учащихся в международных исследованиях…………………………………………………………………………..6
Список использованных источников……. ……………………………………. 13
1. Цели и задачи исследований.
Организациями и проведения международных сравнительных исследований оценки образовательных достижений обучающихся являются PISA и TIMSS.
Основной целью международного исследования TIMSS является сравнительная оценка качества математического и естественнонаучного образования в начальной и основной школе. Каждые четыре года оцениваются образовательные достижения учащихся 4 и 8 классов, включающие не только их знания и умения, но и отношения к предметам, интересы и мотивации к обучению. Исследование спланировано таким образом, что его результаты позволяют отслеживать тенденции в математическом и естественнонаучном образовании участвующих стран каждые 4 года, когда учащиеся 4 классов становятся учащимися 8 класса. Таким образом, осуществляется мониторинг учебных достижений учащихся начальной и основной школы, а также изменений, происходящих в математическом и естественнонаучном образовании при переходе из начальной в основную школу.
Дополнительно изучаются особенности содержания школьного математического и естественнонаучного образования в странах-участницах исследования, особенности учебного процесса, а также факторы, связанные с характеристиками образовательных учреждений, учителей, учащихся и их семей. Для этого дополнительно к международному тестированию проводится анкетирование учащихся, учителей и администрации школ, участвовавших в исследовании. Полученные данные позволяют выявить факторы, влияющие на результаты тестирования, и объяснить состояние математического и естественнонаучного образования в странах-участницах исследования.
В проведении исследования и разработке его инструментария принимают участие многие научно-исследовательские центры и профессиональные организации мира: Служба тестирования в области образования (ETS – Educational Testing Service, США), Канадский Центр Статистики (Statistics Canada), Секретариат Международной ассоциации по оценке образовательных достижений (IEA, Нидерланды), Центр обработки данных Международной ассоциации по оценке образовательных достижений (DPC IEA – Data Processing Center IEA, Германия) и др. Для координации усилий специалистов разных стран были созданы совещательные комитеты, состоящие из ведущих специалистов мира. Координация всего исследования осуществлялась Международным координационным центром в Бостонском колледже (ISC – International Study Center, Boston College, США).
PISA (Programme for International Student Assessment)- международная программа по оценке образовательных достижений учащихся.
Цель международного исследования PISA – оценить математическую грамотность и грамотность в области чтения и естествознания 15-16 летних учащихся организаций общего среднего, технического и профессионального, а также послесреднего образования.
В исследовании используется письменная и компьютерная форма контроля (тесты). В тест включены закрытые и открытые задания. Некоторые задания состоят из нескольких вопросов различного уровня сложности, которые относятся к одной и той же жизненной ситуации.
Основными областями для оценки образовательных достижений являются:
2. Математическая грамотность.
Математическая грамотность – способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину.
Анализ заданий, оценивающих математическую грамотность, позволяет выделить относительно небольшой перечень знаний и умений, которые считаются необходимыми для математически грамотного современного человека, с точки зрения международных экспертов. К ним относятся: пространственные представления, пространственное воображение, некоторые свойства пространственных фигур, использование масштаба, нахождение периметра и площадей нестандартных фигур; умение читать и интерпретировать количественную информацию, представленную в различной форме (таблиц, диаграмм, графиков реальных зависимостей), характерную для средств массовой информации; работа с формулами, знаковые и числовые последовательности; вычисления с рациональными числами, действия с процентами; умение выполнять действия с различными единицами измерения (длины, массы, времени, скорости); использование среднего арифметического для характеристики явлений и процессов, близких к реальной действительности, и др. Успешное выполнение большинства заданий связано с развитием таких важнейших общеучебных умений, как например, умение внимательно прочитать некоторый связный текст, выделить в приведенной в нем информации только те факты и данные, которые необходимы для получения ответа на поставленный вопрос.
3. Как оценивались результаты.
Подход к оценке уровня математической грамотности учащихся PISA .
Пример: «Обменный курс».
Мей-Линг из Сингапура готовилась в качестве студентки по обмену отправиться на 3 месяца в Южную Африку. Ей нужно было обменять некоторую сумму сингапурских долларов (SGD) на южно-африканские рэнды (ZAR).
Вопрос 1 :После возвращения в Сингапур через 3 месяца у Мей-Линг осталось 3900 ZAR. Она обменяла их снова на сингапурские доллары, обратив внимание на то, что обменный курс изменился следующим образом: 1 SGD = 4,0 ZAR.
Пример: «Скейтборд».Сергей большой любитель кататься на скейтборде. Он нередко заходит в магазин «Спорт», чтобы выяснить цены на некоторые товары.
В этом магазине можно купить полностью собранный скейтборд. Но можно купить платформу, один комплект из 4 колес, один комплект из двух держателей колес, а так же комплект металлических и резиновых составных частей и собрать свой собственный скейтборд. Цены в магазине на эти товары представлены в таблице.
Один комплект из 4 колес
Один комплект из 2 держателей колес
Один комплект металлических и резиновых деталей скейтборда
Вопрос 1: Сергей хочет сам собрать для себя скейтборд. Какую наименьшую цену и какую наибольшую цену можно заплатить в этом магазине за все составные части скейтборда?
Вопрос 2: В магазине предлагают на выбор три различных вида досок, два различных комплекта колес, два различных комплекта металлических и резиновых деталей. При этом имеется только один выбор комплекта держателей колес.
Сколько различных скейтбордов может собрать Сергей из предлагаемых составных частей?
Пример: «Садовник». У садовника имеется 32 метра провода, которым он хочет обозначить на земле границу клумбы. Форму клумбы ему надо выбрать из следующих вариантов.
Хватит ли 32 м провода, чтобы обозначить границу клумбы
Подход к оценке уровня математической грамотности учащихся TIMSS .
В связи со сложностью задач, а именно, оценки уровня образовательных достижений по математике и естествознанию учащихся 4 и 8 классов при условии временных ограничений при тестировании и невозможности предоставления всем учащимся возможности выполнить все задания международного банка (который содержит несколько сотен заданий по математике и естествознанию), при конструировании международного теста и обработке результатов используется современная теория тестирования (IRT – Item Response Theory). Данная теория позволяет на основе выполнения учащимися ограниченного числа заданий (60-70) и с учетом их личностных характеристик, характеристик учителей и образовательных учреждений (ответов на вопросы анкет) определить количественные показатели для каждого учащегося и каждой страны, которые характеризуют вероятность выполнения всех заданий международного банка отдельными учащимися или всей выборкой учащихся.
Результаты международного тестирования по математике и естествознанию для учащихся 4 и 8 классов обрабатываются и анализируются отдельно. В результате статистической обработки результатов исследования каждому учащемуся приписываются баллы по международной 1000-бальной шкале отдельно за выполнение заданий по математике и естествознанию.
Международные шкалы результатов учащихся 4 и 8 классов были построены в 1995 году с учетом того, что среднее значение средних баллов всех стран-участниц исследования было принято за 500 со стандартным отклонением 100. Результаты всех последующих исследований отображаются на шкале 1995 года, что позволяет обеспечить сравнение результатов и выявление тенденций в их изменении.
В рамках данной модели образование рассматривается с позиции трех уровней:
-Планируемый уровень — социальный заказ учебному заведению. На планируемом уровне формируются официальные цели образования и совокупность педагогических и методических идей, накопленных в обществе, которая отражается в учебных программах и методических пособиях.
— Реализуемый уровень — реальный учебный процесс учебного заведения. На реализуемом уровне преподаватель учебного заведения формирует планируемое содержание образования в реальном учебном процессе.
— Достигнутый уровень — результаты обучения в учебном заведении. На достигнутом уровне оцениваются образовательные достижения учащегося, его знания, навыки и отношения.
При оценке образовательных достижений по математике используются задания различного типа (с выбором ответа, с кратким и полным развернутым ответом, практические задания). Задания разрабатываются по следующим темам: числа, алгебра, измерения, геометрия, работа с данными. Оцениваются следующие навыки: знания фактов и процедур, использование понятий, решение рутинных проблем, анализ, выдвижение гипотез, оценка, доказательства и другие.
Задания,аналогичные заданиям PISA с критериями оценивания по направлению «Естественнонаучная грамотность»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Естественнонаучная грамотность PISA
Это способность использовать естественнонаучные знания для постановки вопросов, освоения новых знаний, объяснения естественнонаучных явлений и формулирования выводов, основанных на научных доказательствах в отношении естественнонаучных проблем;
понимать основные особенности естествознания как формы человеческого познания;
демонстрировать осведомленность о влиянии естественных наук и технологий на материальную, интеллектуальную и культурную сферы жизни общества;
проявлять активную гражданскую позицию по вопросам, связанных с естествознанием.
Уровень естественнонаучной грамотности
В 2018 году 78,8% российских обучающихся достигли и превысили пороговый (второй по шкале PISA) уровень естественнонаучной грамотности.
На 0,3% увеличилось количество обучающихся, не достигших первого уровня естественнонаучной грамотности, почти на 3% увеличился первый уровень.
Число обучающихся, достигших наивысших уровней естественнонаучной грамотности, составило 3,1%, что на 0,6% меньше, чем в предыдущем цикле исследования.
Измерительный инструментарий исследования PISA по оцениванию естественнонаучной грамотности составляют задания, направленные на проверку компетенций:
научно объяснять явления;
понимать основные особенности естественнонаучного исследования;
интерпретировать данные и использовать научные доказательства для получения выводов.
Блок заданий включают в себя:
описание реальной ситуации, представленное, как правило, в проблемном ключе,
+ ряд вопросов-заданий, относящихся к этой ситуации.
При этом каждый из вопросов-заданий классифицируется по следующим категориям:
компетенция, на оценивание которой направлено задание;
тип естественнонаучного знания, затрагиваемый в задании;
познавательный уровень (или степень трудности) задания
Задания, аналогичные заданиям PISA c критериями оценивания по направлению «Естественнонаучная грамотность»
Стихийные явления на территории России
Азиатское побережье Тихого океана относится к числу самых неспокойных в геологическом отношении районов планеты. Здесь часто происходят и подводные землетрясения, которые порождают в океане огромные волны — цунами. Сильные извержения происходят в этой части страны довольно часто, но ввиду малонаселённости территории большой угрозы для людей они не представляют. Здесь же, на Тихоокеанском побережье, находится единственный в стране район современного вулканизма.
Кроме того, во всех горных районах страны достаточно обычны обвалы, оползни, селевые потоки и снежные лавины.
В 2002 г. россияне стали свидетелями страшной трагедии. В Кодорском ущелье на Кавказе произошло катастрофическое обрушение ледника Колка. О возможности такого бедствия уже давно предупреждали гляциологи, работающие на Кавказе. К сожалению, практически никаких мер по защите населения ущелья не было предпринято. Катастрофа повлекла за собой многочисленные человеческие жертвы.
Прочитайте текст и ответьте на вопросы.
Назовите, какие острова и полуостров, относящиеся к территории России, являются единственным в стране районом современного вулканизма?
Компетенции и умения: научное объяснение явлений (вспомнить и применить соответствующие естественнонаучные знания)
Тип научного знания: науки о Земле и Вселенной
Контекст: окружающая среда(местный/национальный)
Познавательный уровень: низкий
Формат вопроса: с открытым ответом
Какие процессы часто являются толчком и приводят к возникновению обвалов, оползней, селевых потоков и снежных лавин?
Компетенции и умения: научное объяснение явлений (вспомнить и применить соответствующие естественнонаучные знания)
Тип научного знания: науки о Земле и Вселенной
Контекст: окружающая среда(местный/национальный)
Познавательный уровень: низкий
Формат вопроса: с открытым ответом
Толчком для начала движения могут стать землетрясения, сильные дожди, неосторожно брошенный камень или даже громкий звук.
Другие варианты ответа
С чем связаны частые землетрясения, извержения вулканов и цунами на территории Азиатского побережья России?
Компетенции и умения: интерпретация данных и использование научных доказательств для получения выводов.
Тип научного знания: науки о Земле и Вселенной
Контекст: окружающая среда(местный/национальный)
Познавательный уровень: средний
Формат вопроса: с развёрнутым ответом
В ответе говорится о том, что данная область России находится на стыке 2-х литосферных плит и входит в Тихоокеанское огненное кольцо
Другие варианты ответа
Природными причинами обвалов могут быть:
А) Воздействие сейсмических толчков;
Б) Неправильное проведение работ при строительстве;
В) Горные разработки;
Г) Увеличение крутизны склона в результате подмыва водой;
Компетенции и умения: научное объяснение явлений (вспомнить и применить соответствующие естественнонаучные знания)
Тип научного знания: науки о Земле и Вселенной
Контекст: окружающая среда(местный/национальный)
Познавательный уровень: низкий
Формат вопроса: с простым множественным выбором ответа.
Другие варианты ответа
Прочитайте текст и ответьте на вопросы
Природопользование представляет собой систему взаимоотношений человека с природой. Составными частями природопользования являются: изучение, освоение, преобразование и охрана природной среды.
Поэтому необходимо не только изучать пути вовлечения природных ресурсов в хозяйственную деятельность человека, но и находить пути и разрабатывать мероприятия по восстановлению, преобразованию и охране естественных ресурсов и природной среды.
Какие виды деятельности относятся к рациональному природопользованию? Обведите «да» или «нет» для каждого утверждения
А) Создание заповедных территорий
Б) Повторное применение отходов
Г) Образование культурных ландшафтов
Компетенции и умения: интерпретация данных и использование научных доказательств для получения выводов.
Тип научного знания: науки о Земле и Вселенной
Содержание: качество окружающей среды
Формат вопроса: с простым множественным выбором ответа
Задание 2: Природопользование
Как вторичное использование сырья решает проблему истощения ресурсов и загрязнения окружающей среды?
Компетенции и умения : интерпретация данных и использование научных доказательств для получения выводов.
Тип научного знания : науки о Земле и Вселенной
Контекст : окружающая среда(глобальный)
Познавательный уровень : средний
Формат вопроса : развёрнутый ответ
Ожидаемый ответ: экономить ресурсы, так как можно уменьшить добычу и сократить количество отходов, за счет превращения их в нужную продукцию
Другие варианты ответа
Задание 3: Природопользование
Может ли отдельный человек внести вклад в сбережение ресурсов воды, как это сделать?
Компетенции и умения : интерпретация данных и использование научных доказательств для получения выводов.
Тип научного знания : науки о Земле и Вселенной
Контекст : окружающая среда(личностный)
Содержание: природные ресурсы
Познавательный уровень : средний
Формат вопроса : развёрнутый ответ
Примерный ответ: да, экономно использовать воду: следить, чтобы кран не капал, экономить воду при использовании душа, а не ванны, закрывать кран. Не засорять водоемы, не мыть в них автомобили, не сливать в водоемы бытовые отходы
Другие варианты ответа
Задание 4: Природопользование
Международный символ переработки обозначает, что упаковка может быть переработана или уже изготовлена из перерабатываемого сырья. Переработка или утилизация отходов позволяет повторно использовать такие материалы, как стекло, бумага, железо, аккумуляторы, батареи, ткани и пластик.
Если вы будете отдавать предпочтение таким товарам, то вы участвуете в рациональном природопользовании путем:
А) Комплексной переработки сырья
Б) Создании водооборотных циклов
В) Вторичного использования ресурсов
Г) Создании новых технологий
Компетенции и умения : интерпретация данных и использование научных доказательств для получения выводов.
Тип научного знания : науки о Земле и Вселенной
Контекст : окружающая среда(личностный)
Содержание: природные ресурсы
Познавательный уровень : средний
Формат вопроса : с простым выбором ответа
Ситуационные задачи как средство формирования естественнонаучной функциональной грамотности обучающихся
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Ситуационные задачи как средство формирования естественнонаучной функциональной грамотности обучающихся
Ключевые слова: ситуационная задача, грамотность, функциональная грамотность, естественнонаучная грамотность.
Новые условия образовательной политики, компетентностный подход в обучении требуют формирования у обучающихся разных видов функциональной грамотности, в том числе естественнонаучной.
В исследованиях PISA «грамотность» подразумевает набор определенных компетентностей.
Компетентность понимается как способность применять полученные в школе знания и умения в реальных жизненных ситуациях.
• использовать естественнонаучные знания,
Это требует от естественнонаучно-грамотного человека следующих компетентностей:
• научно объяснять явления,
• оценивать и планировать научные исследования,
• научно интерпретировать данные и доказательства.
Одним из новых методических ресурсов является ситуационная задача, сочетающая компетентностно ориентированный подход с традиционным содержанием образования. Ситуационная задача позволяет обучать школьников решать жизненные проблемы с помощью предметных знаний, которые относятся к понятию методических ресурсов. Они дают возможность представить предметные и метапредметные результаты образования в комплексе умений и навыков, основанных на знаниях за счёт усвоения разных способов деятельности, методов работы с информацией.
Ситуационная задача – это прием обучения нового поколения, сочетающий в себе целый ряд функций:
· Функция организации познавательной деятельности учащихся — решение ситуационных задач способствует формированию у школьников естественнонаучной грамотности как способности учащихся использовать естественнонаучные знания для выделения в реальных ситуациях проблем, которые могут быть исследованы и решены с помощью научных методов, для получения выводов, основанных на наблюдениях и экспериментах.
· Правильно организованная самостоятельная учебная деятельность школьников дает возможность учащимся самостоятельно приобретать знания, проверять свои достижения с помощью разноуровневых заданий, вести учет результатов.
· Корректирующая функция в форме сводной таблицы позволяет учителю оценивать результаты работы учащихся, а также осуществлять корректировку в качестве формирующего оценивания.
С другой стороны, ситуационная задача – это способ оценки образовательных результатов обучающихся, так как обучение учащихся решению проблем предполагает освоение универсальных способов деятельности, применимых в самых разных ситуациях.
Результаты решения ситуационных задач оцениваются с помощью таблицы
«Матрица оценивания выполнения ситуационных заданий»
Где (в классе, дома) и как (само стоя тельно, в группе) вы полнено задание
Понимание представленной информации (задания)
Предложение способа решения проблемы
Обоснование способа решения проблемы (своего выбора)
Математическая грамотность
Математическая грамотность
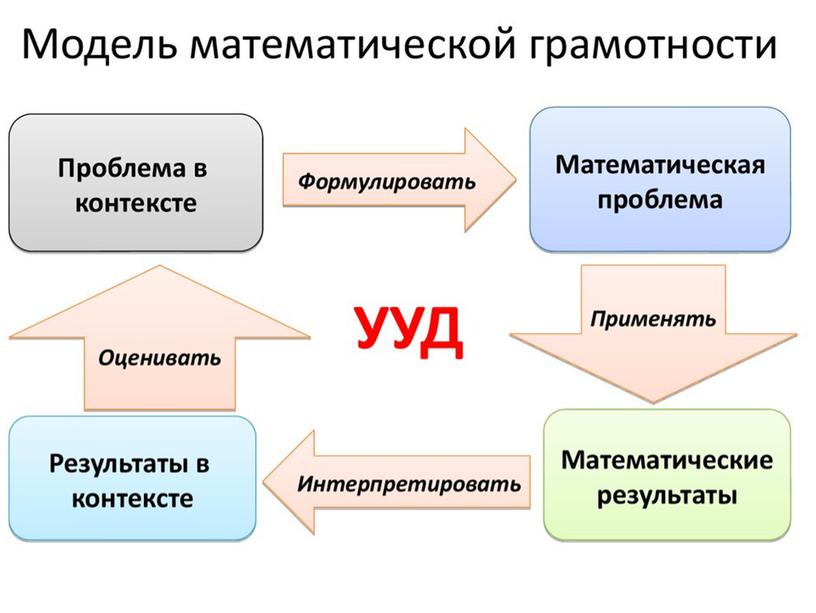
Определение «Математическая грамотность – это способность индивидуума проводить математические рассуждения и формулировать, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира
«Математическая грамотность – это способность индивидуума проводить математические рассуждения и формулировать, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира.
Она включает использование математических понятий, процедур, фактов и инструментов, чтобы описать, объяснить и предсказать явления.
Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые необходимы конструктивному, активному и размышляющему гражданину.»
Математическая грамотность
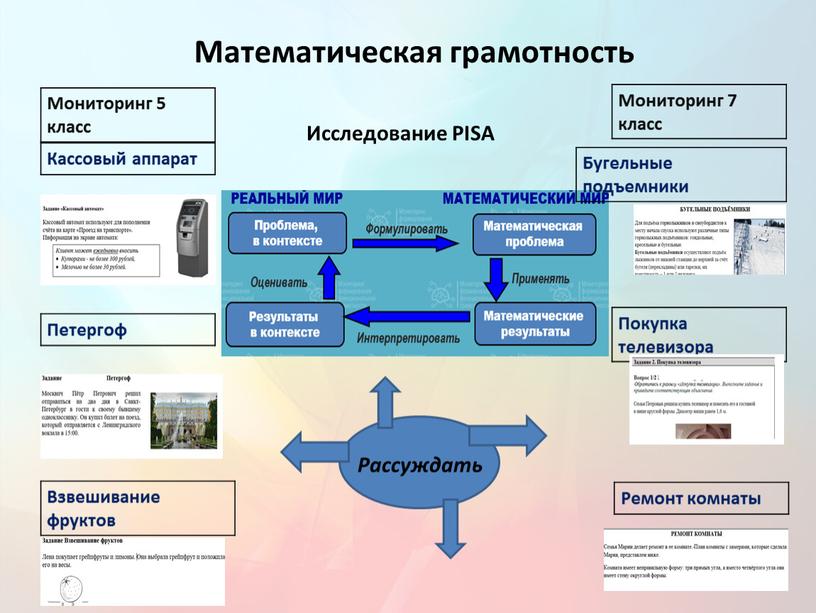
Математическая грамотность Кассовый аппарат
Мониторинг 5 класс
Мониторинг 7 класс
Математическая грамотность
Математическая грамотность
PISA-2021 Особое внимание к оценке математических рассуждений
Особое внимание к оценке математических рассуждений.
Новая точка зрения на связь между математическими рассуждениями и решением поставленной проблемы:
Для решения проблемы математически грамотный учащийся сначала должен увидеть математическую природу проблемы, представленной в контексте реального мира, и сформулировать ее на языке математики.
Это преобразование требует математических рассуждений и, возможно, является центральным компонентом того, что значит быть математически грамотным.
Структура оценки математической грамотности
Структура оценки математической грамотности
Математическое содержание, которое используется в тестовых заданиях (предметное ядро функциональной грамотности):
Изменения и зависимости (алгебра)
Пространство и форма (геометрия)
Неопределенность и данные (ТВ и статистика)
Количество (арифметика)
Когнитивные процессы (составляющие интеллектуальной деятельности), которые описывают, что делает ученик, чтобы связать контекст, в котором представлена проблема, с математикой, необходимой для её решения
формулировать ситуацию математически
применять математические понятия, факты, процедуры
интерпретировать, использовать и оценивать результаты
рассуждать
Контекст, в котором представлена проблема.
Личная жизнь – Мир человека Общественная жизнь – Мир социума
Образование/профессиональная деятельность – Мир профессий
Научная деятельность – Мир науки
Мягкий» мониторинг Контекст: Личная жизнь
Контекст:
Личная жизнь
Образование/
профессии
Общественная жизнь
Научная деятельность
Когнитивная область:
формулировать
применять
интерпретировать/оценивать
рассуждать
Область содержания:
Изменения и зависимости
Пространство и форма
Неопределенность и данные
Количество
Основные положения:
Соответствие ФГОС
Актуальность мат. содержания (по классам)
Использование компьютера
Принципы:
Мотивация (возраст, интерес, доступность)
Реалистичность
Проблемность
Вариативность способов решения
Структура:
Текст-описание – вербальный, графический
Иллюстрации
Справочный материал
Вопрос – сложность от 1 до 3; оценивание – 1-2 балла
Характеристика задания Область содержания (всего 4 данные области): пространство и форма; изменение и зависимости; неопределенность и данные; количество
Область содержания (всего 4 данные области): пространство и форма; изменение и зависимости; неопределенность и данные; количество.
Контекст (всего 4 контекста): общественная жизнь; личная жизнь; образование/профессиональная деятельность; научная деятельность.
Мыслительная деятельность (всего 4 деятельности): рассуждать; формулировать; применять; интерпретировать.
Объект оценки (предметный результат): например, чтение графиков реальных зависимостей.
Уровень сложности: 1, 2 или 3.
Формат ответа: с развёрнутым ответом; с выбором ответа; с кратким ответом.
Критерии оценивания (1 или 2 балла): полный ответ – 2 балла, частично верный ответ – 1 балл.
Использование заданий для оценки и формирования математической грамотности
Использование заданий для оценки и формирования математической грамотности
Для достижения целей мониторинга математической грамотности предлагается использовать блок заданий, рассчитанный на 20 минут выполнения. Предлагается такая структура блока: 2 задания (сюжета) по 2 вопроса в каждом задании, всего 4 вопроса.
Суммарно в каждый блок входят:
-задания из 2-3-х (из 4-х) областей математического содержания,
-задания из 2-х (из 4-х) контекстов,
-задания из 3-4-х (из 4-х) мыслительных процессов;
-задания трёх видов по сложности: одно лёгкое, два средних, одно сложное;
-задания со следующими критериями оценивания: лёгкое задание оценивается одним баллом, остальные –2-мя баллами;
общая сумма баллов за верно выполненный блок заданий – 7.
Структура блока для мониторинга математической грамотности
Структура блока для мониторинга математической грамотности
Пример «Тормозной путь». 7 класс
Пример «Тормозной путь». 7 класс
Тормозным путем называется расстояние, которое прошло транспортное средство от момента нажатия на педаль тормоза до полной остановки. При движении автомобиля его тормозной путь зависит от скорости и от состояния дорожного полотна, связанного с погодными условиями.
Вопрос 1.
Используя данные диаграммы «Зависимость
длины тормозного пути от скорости автомобиля
и состояния дороги», проверьте истинность
следующих утверждений и заполните таблицу.
Чем хуже состояние дороги, тем короче тормозной путь
Чем больше начальная скорость, тем длиннее тормозной путь на сухом асфальте
Длина тормозного пути на мокром асфальте более чем в 1,5 раза больше длины тормозного пути на сухом асфальте
Вопрос 2 Для расчета ориентировочной длины тормозного пути легкового автомобиля можно использовать формулу:
Автомобиль, двигавшийся на резине без шипов по мокрой дороге со скоростью 60км/ч, начал торможение. Вычислите длину его тормозного пути. Результат округлите до целого.
Особенности движения автомобиля
на резине без шипов по сухому асфальту по ровной траектории
на резине без шипов по мокрой дороге
по укатанному снегу
по обледенелой дороге
Характеристики задания «Тормозной путь»
Характеристики задания «Тормозной путь»
Апробация. Результаты Положительное: учащиеся практически не пропускают задания, очень мало ответов «не знаю», «не могу решить», есть положительные отзывы о задачах («интересное задание»)
Положительное: учащиеся практически не пропускают задания, очень мало ответов «не знаю», «не могу решить», есть положительные отзывы о задачах («интересное задание»).
Отрицательное: значительная часть демонстрирует неготовность вычленять математические аспекты из реальной ситуации, выбирать существенную информацию, обрабатывать, используя математический аппарат. Не понимают, когда надо привлекать жизненный опыт, а когда математические знания.
Не понимают, что означает «доказать», «обосновать».
Нет развития навыков смыслового чтения. Плохо читают условие, не сопоставляют текстовую и табличную, графическую информацию, не используют справочную информацию.
Проявляют известные недостатки: несформированность чувства числа, недостаточность вычислительной подготовки, развития геометрических представлений, воображения, навыков измерения геометрических величин, неумение решать даже учебные задачи.
Недостатки в овладении метапредметными умениями работать с нетрадиционным заданием, в частности, с задачей, отличной от текстовой, для которой известен способ решения; работать с информацией, представленной…
Недостатки в овладении метапредметными умениями
работать с нетрадиционным заданием, в частности, с задачей, отличной от текстовой, для которой известен способ решения;
работать с информацией, представленной в различных формах (текста, таблицы, диаграммы, схемы, рисунка, чертежа)
отбирать информацию, если задача содержит избыточную информацию; привлекать информацию, использовать личный опыт
задавать самостоятельно точность данных с учетом условий задачи
моделировать ситуацию
размышлять: использовать здравый смысл, перебор возможных вариантов, метод проб и ошибок
представлять в словесной форме обоснование решения
находить и удерживать все условия, необходимые для решения и его интерпретации
Формирование МГ. Что делать?
Формирование МГ. Что делать?