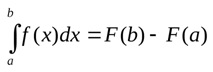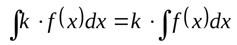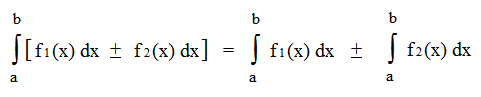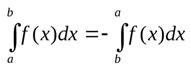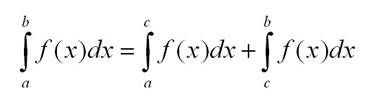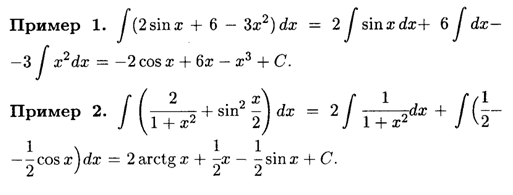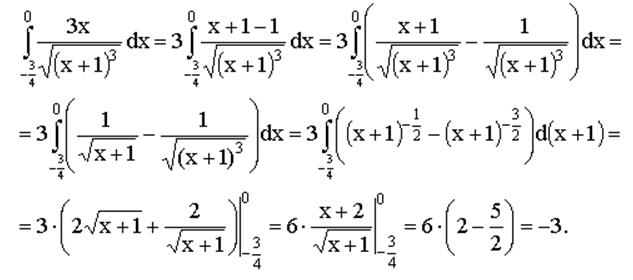в чем разница определенного и неопределенного интеграла
Интегралы для чайников: как решать, правила вычисления, объяснение
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Изучаем понятие « интеграл »
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x).
Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
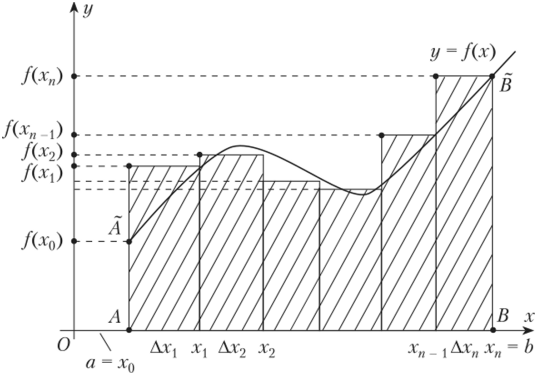
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
Свойства определенного интеграла
Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Интегралы – что это, как решать, примеры решений и объяснение для чайников
За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов
Почему вы не знаете, как решать интегралы
А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.
Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:
Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.
Главная причина незнания – отсутствие понимания практической значимости интегралов.
Нужна помощь в написании работы?
Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Интеграл – что это?
Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.
Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.
Метод исчерпывания для определения площади круга
В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.
Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.
Объясняем понятие «Интеграл»
Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.
Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».
Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.
Интеграл записывается так:
Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).
Неопределённый интеграл
Неопределенный интеграл не имеет границ интегрирования.
Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».
Определённый интеграл
В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.
Точки A и B на оси X – есть ограничение зоны определения интеграла
Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:
Таблица интегралов для студентов (основные формулы)
Скачайте формулы интегралов, они вам еще пригодятся
Как вычислять интеграл правильно
Существует несколько простейших операций для преобразования интегралов. Вот основные из них:
Вынесение константы из-под знака интеграла
Разложение интеграла суммы на сумму интегралов
Если поменять местами a и b, знак изменится
Можно разбить интеграл на промежутки следующим образом
Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.
Примеры вычисления интегралов
Решение неопределенного интеграла
Решение определенного интеграла
Базовые понятия для понимания темы
Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.
Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.
Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.
Приращение – количественное изменение функции при некотором изменении аргумента.
Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.
Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.
Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.
Заключение
Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.
Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:
Первообразная
Определение. Непрерывная функция F(x) называется первообразной функции f(x), если на промежутке X, если для каждого 
Операция нахождения первообразной функции f(x), называется интегрированием.
Неопределенный интеграл
Неопределённый интеграл-это совокупность всех первообразных функции f(x). В общем случае, нахождение неопределённого интеграла выглядит следующим образом:

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования. Неопределённый интеграл представляет собой, как бы, «пучок» первообразных, из-за наличия постоянной интегрирования.
Дифференциал-произвольное, бесконечно малое приращение переменной величины.
Свойства неопределённого интеграла
Таблица основных неопределённых интегралов
В виде

где f(x)-подынтегральная функция, F(x)-первообразная функция функции f(x), dx-дифференциал, C-константа интегрирования.
Определённый интеграл
Определенный интеграл— Приращение одной из первообразных функции f(x) на отрезке [a;b].
Общий вид определённого интеграла:
где f(x)–подынтегральная функция, a и b-пределы интегрирования, dx-дифференциал
Свойства определённого интеграла: см. св-ва определённого интеграла.
Определённый интеграл вычисляется по формуле Ньютона –Лейбница:
Применение определённого интеграла:
1. Нахождение площади криволинейной трапеции
2. Нахождение величины скорости v по заданному закону ускорения a(t) за промежуток времени [t1;t2], т.е
Пример: Точка движется по закону ускорения a(t)=t+1. Найти величину ее скорости за промежуток времени [2;4] секунд.
Решение:
3. Нахождение пути S по закону изменения скорости v(t) за промежуток времени [t1;t2], т.е.
Пример: Найти путь, который проделала материальная точка за промежуток времени [2;4], двигаясь со скоростью, которая изменялась по закону: v(t)=2t+2.
Решение:
Стоит отметить, что, на сегодняшний день, интегральное и дифференциальное исчисление занимают лидирующие позиции в математике. Советую вам ознакомиться, более подробно, с широким применением интегралов в естествознании.
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Понятие первообразной
Однако на практике значительно чаще встречается прямо противоположная задача. Известно, как меняется скорость тела, и найти требуется путь, пройденный им. В таком случае необходимо по производной определить ту функцию, которая «подверглась» дифференцированию.
Задание. Известна производная функции у(х):
В этом примере мы выполнили операцию, обратную дифференцированию. В математическом анализе он называется интегрированием. Если интегрируют некоторую произвольную функцию f(х), то в итоге получают новую функцию, которую чаще всего обозначают как F(x). Её называют первообразной функции f(x).
Приведем несколько примеров первообразной:
Последний пример показывает, что иногда первообразная может и совпадать с исходной функцией.
Задание. Докажите, что функция
Первообразные встречаются и в ряде практических задач, особенно в тех, где рассматривается движение тел.
Задание. Автомобиль Buggati Veyron разгоняется от 0 до 40 м/с за 4 секунды. Какое расстояние проедет эта машина за эти 4 секунды, если разгон осуществляется равномерно?
Решение: Если за 4 секунды машина разгоняется до 30 м/с, то за одну секунду она увеличивает скорость на
Примечание – в будущем мы научимся более строго решать такие задачи, и «угадывать» подходящую первообразную не придётся.
Бесконечное количество первообразных
Оказывается, что g1 также является первообразной для у. То есть у одной функции у = 4х 3 есть сразу две первообразных:g = x 4 и g = x 4 + 1! Более того, можно доказать, что у любой функции есть бесконечное количество первообразных!
Действительно, рассмотрим сразу все функции
где С – некоторая константа, то есть параметр. В данном случае можно сказать, что мы рассматриваем не одну функцию, а семейство функций. Продифференцируем g:
Данная особенность операции интегрирования может быть сформулирована в виде следующей теоремы:
Можно дать и графическую иллюстрацию этого правила. Построим произвольный график g = F(x). Далее построим ещё один график
Очевидно, что он может быть получен параллельным переносом первого графика на С единиц вверх:
Теперь в какой-нибудь точке х0 проведем касательные к обоим графикам первообразных. Очевидно, что они будут иметь одинаковый угол наклона, так как по сути тоже могут быть получены параллельным переносом:
Если же углы наклона касательных совпадают, то и производные в этих точках также равны.
В связи с наличием у каждой функции бесконечного количества первообразных их часто записывают в общем виде. Например, пусть надо записать первообразную для
Однако 2х 2 – это лишь одна из бесконечного множества первообразных. Все вместе они образуют семейство, которое записывается так:
Неопределенный интеграл
Каждая математическая операция имеет какое-то особое обозначение. Например, чтобы показать, что мы дифференцируем некоторую функцию, мы ставим после неё штрих (и при необходимости берем в скобки):
Напомним, что операция нахождения первообразной называется интегрированием. Для ее обозначения используется особый знак – интеграл. Например, мы знаем, что первообразная для у = х 2 – это семейство функций вида
Рассмотрим элементы записанного нами равенства:
Исходная функция – это та самая функция, для которой необходимо найти первообразную, то есть интегрируемая функция. Справа от знака «равно» как раз записывается первообразная. Сразу после первообразной надо писать «+ С». Тем самым мы показываем, что у интегрируемой функции есть бесконечное количество первообразных.
После интегрируемой функции стоит так называемый дифференциал dх (читается как «дэ икс»). В данном случае он указывает, что именно буквой х мы обозначаем переменную в интегрируемой функции. Его значение мы разберем несколько позже. Пока что надо запомнить, что после интегрируемой функции необходимо писать «dx». В целом вся запись
читается так: «интеграл от два икс по дэ икс равен икс в квадрате плюс цэ».
В чем разница между первообразной и интегралом? Первообразная – это функция, при дифференцировании которой получается исходная функция. Интеграл же – это не функция, а целое семейство функций (или их множество), которое включает в себя сразу все первообразные интегрируемой функции.
Так как интегрирование – это действие, обратное дифференцированию, то мы можем проверить результат своих вычислений. Пусть мы записали, что
Получили подынтегральное выражение. Значит, мы всё сделали правильно.
Здесь важно заметить, что в математике существует сразу несколько видов интегралов, каждый из которых имеет разное определение. Здесь описан так называемый «неопределенный интеграл». Несложно догадаться, что существует ещё и «определенный интеграл», который мы рассмотрим на следующих уроках. Теперь можно дать следующее определение:
Задание. Найдите неопределенный интеграл
Решение. Вспомним таблицу производных элементарных функций. Производная синуса равна косинусу:
Заметим, что непосредственно из определения следует важное свойство неопределенного интеграла – производная интеграла равна его подынтегральному выражению:
Грубо говоря, операции интегрирования дифференцирования «сокращают» друг друга.
Задание. Вычислите производную:
Таблица первообразных
Как же вычислять интегралы? Проще всего начать с тех функций, которые уже есть в таблице производных. Напомним, как она выглядит:
Из определения первообразной следует, что для тех функций, которые указаны во втором столбце таблицы, одной из первообразных является соответствующая функция из первого столбца. То есть можно составить такую таблицу первообразных:
Обратите внимание на третью строку снизу. Здесь произошло небольшое изменение – вместо первообразной lnx мы записали ln |x|, то есть использовали модуль числа. Дело в том, что функция
определена при любом значении аргумента, кроме нуля. В то же время функция
не определена при отрицательных значениях х, так как под знаком логарифма не может стоять отрицательное число. Однако области определения интегрируемой функции и ее первообразной должны совпадать. Использование модуля обеспечивает выполнение этого условия.
Полученная нами таблица интегралов не совсем удобна. Предположим, нам надо проинтегрировать функцию
Однако можно догадаться, что в качестве подходящей первообразной можно взять функцию
В связи с этим есть смысл немного подкорректировать таблицу первообразных таким образом, чтобы в первом столбце стояли стандартные функции без неудобных множителей. В результате таблица примет следующий вид:
Можно доказать, что каждое равенство в третьем столбце является справедливым. Возьмем, например, равенство
Получили подынтегральное выражение, а это значит, что равенство справедливо. Таким же образом можно доказать и все остальные равенства в таблице.
Задание. Вычислите неопределенный интеграл:
Решение. Этот интеграл присутствует в таблице (7-ая строка), а потому мы просто переписываем равенство из неё:
Задание. Найдите первообразную функции
Правила вычисления интегралов
Что делать в том случае, если надо вычислить интеграл, которого нет в таблице? Существует три несложных правила интегрирования, которые могут помочь в такой ситуации.
Докажем это правило. Для этого просто продифференцируем правую часть равенства:
Получили именно то выражение, которое стоит под знаком интеграла в левой части равенства. Это значит, что формула справедлива.
Рассмотрим пример использования этого правила. Пусть надо найти первообразную функции
Здесь мы представили исходный интеграл как сумму двух более простых интегралов, которые являются табличными
Обратите внимание, что мы не стали складывать константы интегрирования С как подобные слагаемые и писать 2С. Дело в том, что С – это некоторое произвольное число. Но если сложить два произвольных числа, то в итоге получится третье произвольное число, которое также будет обозначаться как С! Поэтому обычно константу С просто дописывают в самом конце решаемого примера.
Естественно, что правило сложения интегралов работает и в случае суммы не двух, а большего количества слагаемых.
Задание. Вычислите неопределенный интеграл
Возможна ситуация, когда мы не уверены в правильности полученного решения. В таком случае можно легко проверить себя, просто продифференцировав получившийся интеграл. В итоге мы должны получить исходную функцию (подынтегральное выражение):
Следующее правило позволяет выносить множитель из-под знака интеграла.
Для доказательства тождества снова продифференцируем его левую часть:
Получили как раз то выражение, которое стоит под интегралом справа. Следовательно, формула верна.
Рассмотрим несколько простейших примеров использования этого метода интегрирования неопределенных интегралов:
Естественно, что правила 1 и 2 можно комбинировать друг с другом, решая более сложные примеры.
Задание. Вычислите неопределенный интеграл от квадратичной функции
Первые два правила достаточно просты и напоминают аналогичные правила дифференцирования. А вот третий метод вычисления неопределенного интеграла более сложный.
Проиллюстрируем его на примере. Пусть надо найти первообразную для функции
Но в нашем случае под знаком косинуса стоит не х, а выражение 5х + 7, являющееся линейной функцией. Поэтому, согласно правилу, мы должны написать впервообразной не sinx, а sin (5x + 7), то есть изменить аргумент. Также надо добавить перед синусом «поправочный множитель», равный 1/k, то есть в нашем случае 1/5:
Проверим себя. Продифференцируем получившуюся первообразную. При этом мы используем правило дифференцирования сложной функции:
Получили ту самую функцию, которую и надо было проинтегрировать.
Приведем ещё несколько примеров использования правила 3:
Напомним, что при изучении производной мы познакомились также с правилами дифференцирования произведения, дроби и сложной функции. Используя их, мы могли найти производную для почти любой функции, которую только могли записать. С решением неопределенных интегралов ситуация значительно сложнее. С помощью приведенных трех правил не получится вычислить такие интегралы, как
Более того, в записанной нами таблице интегралов отсутствует ряд элементарных функций, поэтому мы не сможем даже проинтегрировать такую простую функцию, как
Дело в том, что задача интегрирования является значительно более сложной, чем задача дифференцирования. Отметим три момента. Во-первых, в нашей школьной таблице интегралов, содержащей всего 11 формул, указаны лишь самые простые элементарные функции. Существуют справочники, где в качестве табличных указаны интегралы десятков, а то и сотен функций. Во-вторых, есть и более сложные правила интегрирования, которые изучаются уже в институте. В-третьих, существуют такие элементарные функции, первообразную которых в принципе невозможно записать, используя элементарные функции (синус, косинус, логарифм и т.п.). В связи с этим приходится вводить в рассмотрение новые специальные функции, а также использовать приближенные методы вычислений.
Физический смысл неопределенного интеграла
Напомним физический смысл производной – если известен закон движения материальной точки, то есть некоторая функция S(t), то производная этого закона будет выражать скорость тела в момент времени t:
Отсюда прямо вытекает физический смысл первообразной. Если известен закон изменения скорости v(t), то его первообразная будет являться законом движения S(t). Точнее говоря, законом движения будет являться только одна из первообразных, так как их существует бесконечно много.
Задача. Скорость тела в произвольный момент времени t может быть вычислена по закону
Найдите закон движения материальной точки S(t). Известно, что в начальный момент времени тело находилось в точке с координатой 1,5, то есть S(0) = 1,5.
Решение. Нам надо просто проинтегрировать функцию v(t):
Интеграл вычислен, но это ещё не закон движения, ведь в нем присутствует константа интегрирования. Как от неё избавиться? Надо использовать условие, согласно которому S(0) = 1,5. В общем виде закон движения имеет вид
Мы нашли конкретное значение константы интегрирования. С учетом этого закон движения (1) примет вид: