в чем разница между передаточным отношением и передаточным числом

Передаточное отношение, передаточное число

Передаточное отношение – это отношение мгновенных угловых или линейных скоростей ведущего и ведомого звеньев. u = ω₁/ω₂.

Передаточное число – это отношение чисел зубьев или диаметров (радиусов) ведомого и ведущего звеньев. i = z₂/z₁.

В производственном лексиконе эти два понятия зачастую путают, поскольку в численном выражении u = i. Определим uи i при последовательном и параллельном соединении зубчатых колес.

Последовательное соединение (рис.4.3).

u _1-4 = ω₁/ω₂* ω₂/ω₃* ω₃/ω₄ = ω₁/ω₄

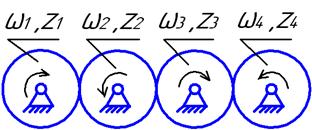
Видим, что промежуточные шестерни z₂ иz₃не влияют на передаточное отношение и передаточное число. Эти шестерни называются паразитными. Они

Рис. 4.3устанавливаются в двух случаях:

1 – для изменения направления вращения; 2 – для получения большого межосевого расстояния при малых поперечных габаритах передачи.

Параллельное соединение (рис.4.4).

u _1-4 = ω₁/ω₂* ω₃/ω₄ = ω₁/ω₄,

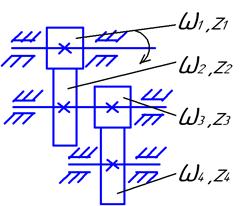
ω₂ = ω₃ – это один вал.

При параллельном соединении нет паразитных шестеренок. Больше того, у зубчатых колес 1-й ступени (z₁и z₂) модуль меньше чем модуль колес 2-й ступени (z₃и z₄), поскольку крутящий момент на входе 1-й ступени в i _1-2 = z₂/z₁раз меньше момента на входе 2-й ступени (при условии, что обе

Рис. 4.4ступени редукторные, то есть

Редуктор –понижает обороты, но увеличивает крутящий момент.

Мультипликатор – повышает обороты, но понижает крутящий момент.

Источник

ПЕРЕДАТОЧНОЕ ОТНОШЕНИЕ И ПЕРЕДАТОЧНОЕ ЧИСЛО

Важнейшей характеристикой всякого зубчатого механизма является передаточное отношение. Передаточным отношением называется отношение угловых скоростей колес. Передаточное отношение принято обозначать буквой U и снабжать индексами, указывающими номера зубчатых колес, например U₁₂ = ω₁ ⁄ ω₂. Из рассмотрения зубчатой передачи на рис.5.23 следует:

Передаточное отношение не следует путать с передаточным числом, под которым понимается отношение угловой скорости большего колеса к угловой скорости меньшего, называемого обычно шестерней. Передаточное число всегда больше единицы и знака не имеет.

Рядовой зубчатой передачей (зубчатым рядом) называется зубчатый механизм, образованный зубчатыми колесами с неподвижными осями. Зубчатый ряд состоит из одной или нескольких зубчатых передач. Рассмотрим механизм на рис. 5.24. Он составлен из трех зубчатых передач, образованных колесами z₁, z₂, z₃, z₄, z₅, z₆. Запишем их передаточные отношения:

Производя последовательную подстановку выражений для ω₂, ω₄, ω₅, получим

Полученная формула является частным случаем общего правила, формулируемого следующим образом:

Передаточное отношение рядовой зубчатой передачи равно произведению передаточных отношений входящих в нее зубчатых передач, при этом следует учитывать знаки передаточных отношений составляющих зубчатых передач.

Передаточное отношение также можно выразить через числа зубьев:

Отсюда следует второе правило:

Передаточное отношение рядовой зубчатой передачи равно дроби, в числителе которой стоят числа зубьев выходных колес, а в знаменателе – входных. Знак берется согласно указанному выше правилу знаков. В формуле колесо Z₄ не влияет на численное значение передаточного отношения, но влияет на знак. Такое колесо называется паразитным

РАСЧЕТ РЯДОВОЙ КОРОБКИ ПЕРЕДАЧ

В качестве примера рассмотрим коробку передач легкового автомобиля, в основе которой рядовой зубчатый механизм (рис. 5.24).

Она состоит из входного вала 1, выходного вала 2 и промежуточного вала 3. На промежуточном валу жестко закреплены колеса с числом зубьев Z₁ = 29, Z₂ = 24, Z₃ = 20, Z₄ = 15, Z₅ = 15, на входном валу – колесо Z₆ = 17. На выходном валу подвижно установлены колеса Z₇ = 24, Z₈ = 27, Z₉ = 33. Для включения передачи 1 рычагом переключения передач передвигается кулачковая муфта М₁ направо так, что она кулачками сцепляется с колесом Z₉. Передвигая муфту влево, включаем передачу II, аналогично посредством муфты М₂ происходит включение передач III IY. При указанных числах зубьев колес рассчитаем передаточные отношения на I II III IY передачах:

U I = 29 33 / 17 15 = 3.75

U II ₌ 29 27 / 17 20 = 2.303

U III = 29 21/ 17 24 = 1.49

Вводя в зацепление с колесами Z₅ и Z₁₀ = 34 паразитное колесо Z₁₁, получаем передачу заднего хода с передаточным отношением

ПЛАНЕТАРНЫЕ ЗУБЧАТЫЕ МЕХАНИЗМЫ

Планетарным называется зубчатый механизм, содержащий колеса с подвижными осями. Планетарные зубчатые механизмы широко распространены в технике, особенно транспортной, так как, обладая большим передаточным отношением, имеют малые габариты и вес. Иногда эти механизмы называют эпициклическими, так как траектории точек колес с подвижными осями при внешнем зацеплении представляют эпициклоиды. Простейший планетарный механизм представлен на рис. 5.25. Колесо 2 с подвижной осью называется сателлитом, центральное колесо 1 – солнечным, звено, несущее ось сателлита, называется водилом, его принято обозначать буквой Н.

Если колесо 1 подвижно, степень подвижности механизма, рассчитанная по формуле Чебышева, равна 2, Если остановить колесо 1, получим механизм с W = 1 (рис. 5.25б) Механизмы, у которых W>1, называются дифференциальными (зубчатыми дифференциальными). Если у планетарного механизма остановить водило, оставив колеса свободными, получим рядовую передачу.

Схема планетарных механизмов могут быть очень разнообразными. Практическое применение нашло, в основном, только несколько схем. Наиболее распространенные схемы представлены на рис. 5.26.

Механизм по схеме а получил название механизма Джеймса, а механизм по схеме в – механизм Давида. Наибольшее распространение получила схема а. Она характеризуется высоким к.п.д., практический диапазон передаточных отношений U = 3 – 8. Механизмы по схемам в и г могут иметь очень большие передаточные отношения, но у них низкий к.п.д. По схеме е выполняются мотор – редукторы, представляющие в одном агрегате двигатель и редуктор. Особенно перспективна схема д, здесь всего два колеса, высокий к.п.д., большое передаточное отношение.

АНАЛИТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОГО ОТНОШЕНИЯ И УГЛОВЫХ СКОРОСТЕЙ ПЛАНЕТАРНЫХ МЕХАНИЗМОВ

Кинематический расчет планетарных механизмов значительно более сложен, чем рядовых механизмов. Он основан на методе обращения движения. Рассмотрим его на примере механизма на рис. 5.27. Считаем, что заданы числа зубьев колес Z₁, Z₂, Z₃, Z₄, угловая скорость входного колеса ω₁. Требуется определить передаточное отношение U_1н, угловую скорость выходного звена Н и угловую скорость колеса 2.

Сущность метода обращения движения состоит в следующем: придадим стойке механизма скорость вращения водила ω_н, но в противоположном направлении. Тогда водило окажется неподвижным в абсолютной системе отсчета, а остальные звенья приобретут дополнительную скорость – ω_н. Изобразим обращенный механизм рядом на схеме. Механизм с неподвижным водилом является зубчатым рядом, для него справедливы полученные ранее соотношения:

Здесь верхний индекс Н указывает, что параметры относятся к обращенному механизму. Согласно формуле (5.11) имеем:

Из формулы (5.12) после некоторых преобразований следует:

Полученная формула справедлива для любой схемы планетарного механизма. Она носит название формулы Виллиса.

Если требуется определить передаточное отношение от водила к колесу 1, то, имея в виду, что U_H1 = 1 / U_1H, получим

Зная U_1H, можно найти ω_Н: ω_Н = ω₁ / U_1H. Для определения скорости ω2 следует рассмотреть одну ступень планетарного механизма и изобразить соответствующий ей обращенный механизм (рис.5.28). Для обращенного механизма

Отсюда уже не представляет сложности определить ω₂.

5.25 КИНЕМАТИЧЕСКИЙ АНАЛИЗ АВТОМОБИЛЬНОГО ДИФФЕРЕНЦИАЛА

Рассмотренный метод кинематического исследования применим также к анализу дифференциальных зубчатых механизмов. Одним из наиболее известных является автомобильный дифференциал (рис.5.29). Его назначение – передача движения от карданного вала к колесам автомобиля. Механизм, представленный на рис.5.29, включает главную передачу, образованную коническими колесами Z₁и Z₂, корпус дифференциала, являющийся в то же время водилом дифференциального механизма, нескольких сателлитов Z₄ и двух центральных колес Z₃ и Z₅, жестко посаженных на полуоси колес.

Применим к этому механизму принцип обращения движения, сообщив ему скорость – ω_Н. На рис. представлен обращенный механизм. Для него можно записать

Произведем анализ формулы (5.13). При движении по прямому участку дороги ω₃ = ω₅ = ω_Н, следовательно, дифференциал как бы жестко связывает полуоси, происходит кинематическая блокировка дифференциала. Совершенно по другому ведет себя дифференциал при движении по закруглению. Внешнее колесо движется с большой угловой скоростью, чем внутренне, но так, что их средняя скорость равна скорости водила. Если бы колеса были связаны жесткой осью, происходило бы пробуксовка одного или обоих колес, ухудшая эксплуатацию автомобиля. В том случае, когда одно колесо свободно пробуксовывает, второе колесе неподвижно. Скорость буксующего колеса равно 2ω_Н. В таких случаях применят механическую блокировку дифференциала.

Источник

О зубчатой, ременной, цепной, червячной и планетарной передачах

Незаменимыми помощниками человека в любой его деятельности являются механизмы. Но сам по себе механизм – просто набор деталей. Для того чтобы он работал, его надо обеспечить энергией. Ее подают от отдельного устройства – двигателя или силовой установки при помощи специальных механизмов, называемых передачами. Так уж сложилось исторически – в технике чаще всего используется вращательное движение, хотя применяются и другие виды. При процессе перехода энергии она может меняться, это изменение происходит в соответствии с тем, какое передаточное отношение имеет механизм.

О том, что при этом происходит

Самый простой пример передачи – от вращающегося колеса водяной мельницы к жернову. При этом зачастую происходит изменение первоначальной энергии, полученной колесом от текущей воды, по величине и направлению. Величину такого изменения будет определять передаточное отношение. Оно описывает одну из важнейших характеристик преобразования энергии при вращательном движении, определяемую как отношение частоты или скорости вращения элемента, получающего энергию, к тем же параметрам элемента, отдающего энергию.

Иными словами, передаточное отношение описывает, как изменяется исходная энергия, получаемая от двигателя или любого другого источника энергии (водяного, ветряного колеса, турбины и т.д.), при ее передаче. За всю историю развития техники человечество создало самые разнообразные передачи, для каждой из которых существует передаточное число, являющимся частным от деления скорости ведущего звена на скорость ведомого.

Передаточное отношение ременной передачи

Ременной передачей называют два шкива, которые соединяет ремень, как это показано на рисунке. Возможно, что она была одним из первых способов, которые применял человек. Менялся материал, используемый для изготовления ремня, менялась его форма, но неизменным оставалось передаточное отношение, определяемое как частое от деления скорости ведущего вала, на скорость ведомого, или как результат деления числа оборотов этих валов (n1/n2 или ω1/ω2).
Для ременной передачи оно может быть рассчитано с использованием диаметров (радиусов) шкивов. Передаточное число в таком случае также определяется как частное от деления оборотов.

Если при преобразовании энергии число оборотов понижается, то есть передаточное число больше 1, то передача будет понижающей, а само устройство носит название редуктора. Если результат меньше единицы, то устройство называется мультипликатором, хотя оно также выполняет функции редуктора, только понижающего. Передаточное отношение редуктора позволяет уменьшить число оборотов (угловую скорость), поступающих с ведущего вала на ведомый, увеличив при этом передаваемый момент.

Это свойство редуктора дает возможность добиваться инженерам при проектировании различных устройств изменения параметров передаваемой энергии, а передаточное отношение редуктора служит при этом мощным инструментом в решении поставленной задачи.

Несмотря на значительный возраст, для ременной передачи и сейчас находится работа на автомобиле, она используется как привод генератора, газораспределительного механизма, а также в некоторых других случаях.

Передаточное отношение цепной передачи

В подобной ременной передаче ремень может быть заменен на цепь, в этом случае шкивы также должны быть заменены на звездочки. Полученная передача называется цепной, она знакома каждому, ведь именно такая применяется на велосипедах. Для нее передаточное отношение определяется так же, как для ременной, но можно воспользоваться и соотношением количества зубьев на звездочках (ведущей и ведомой). Однако при таком расчёте передаточное отношение будет обратным, то есть передаточное число определяется делением числа зубьев ведомой звездочки на число зубьев ведущей (z2/z1).

Отличительной особенностью цепной передачи является повышенный уровень шума, а также износ при работе на высоких скоростях, поэтому ее при необходимости использования лучше всего ставить после уменьшения оборотов. В автомобиле возможно применение цепной передачи для привода ГРМ, правда, ограничением такого применения является повышенный уровень шума при ее работе.

Передаточное отношение зубчатой передачи

Так называется механизм, в котором используются колеса с зубьями, находящимися в зацеплении. Она считается наиболее рациональной и востребованной для машиностроения. Существует множество разнообразных вариантов изготовления подобных колес, отличающихся по расположению осей, форме зубьев, способу их зацепления и т.д. Как в случае с цепной, для зубчатой передаточное число определяется делением числа зубьев шестерен (z2/z1).

Многообразие вариантов построения зубчатой передачи предоставляет возможность использовать их в разных условиях, от тихоходного редуктора до высокоточных приводов.

Для зубчатой передачи характерны:

Одной из разновидностей зубчатой передачи считается червячная. Она используется в тех случаях, когда передача момента осуществляется между скрещивающимися валами, для чего применяется такой элемент как червяк, представляющий собой винт специальной конструкции с резьбой. Для определения передаточного отношения червячной передачи выполняют деление количества зубьев колеса (червячного) z2 на число заходов резьбы червяка z1.

Планетарная передача

Этот вид зубчатой передачи, содержащей колеса с геометрическими осями, имеющими возможность перемещения. Что она собой представляет, можно понять из приведенного ниже рисунка. По сути дела, это уже конструкция своеобразного планетарного редуктора, включающего в свой состав некоторое число шестерен, взаимодействующих между собой. У каждой из них свое название – солнце, корона, сателлит.

Для такого планетарного редуктора изменение момента зависит от того, какая из его шестерен неподвижна, на какую подан крутящий момент, и с какой он снимается.

При любом использовании планетарного редуктора, один из трех его элементов будет неподвижен. У такого, планетарного варианта построения передач, по отношению к простой зубчатой или ременной, есть возможность получить существенное изменение момента при небольшом количестве колес и габаритах устройства. В автомобиле у подобного планетарного устройства своя сфера применения – в составе АКПП, а также в гибридных транспортных средствах, для обеспечения совместной работы ДВС и электромотора. Широкое применение планетарного редуктора осуществляется в гусеничной технике.

О главной паре

Практически все виды передач используются в автомобиле – крутящий момент от двигателя проходит цепочку различных устройств и претерпевает изменения, начиная от КПП, главной пары, и заканчивая колесами автомобиля. Все передаточные отношения для КПП и главной пары влияют непосредственным образом на динамику автомобиля.
Поэтому с целью

передаточные отношения, в том числе и для главной пары, должны быть уменьшены. Для улучшения разгонной динамики все должно быть наоборот.

Работа различных механизмов и устройств, в том числе и в автомобиле, не может происходить без преобразования используемой энергии, как по величине, так и по направлению. Оценить и рассчитать величину необходимого изменения, а также его последствия, помогает передаточное отношение.
» alt=»»>

Источник

Передаточное число

Любое подвижное соединение, передающее усилие и меняющее направление движения, имеет свои технические характеристики. Основным критерием, определяющим изменение угловой скорости и направления движения, является передаточное число. С ним неразрывно связано изменение силы – передаточное отношение. Оно вычисляется для каждой передачи: ременной, цепной, зубчатой при проектировании механизмов и машин.

Перед тем как узнать передаточное число, надо посчитать количество зубьев на шестернях. Затем разделить их количество на ведомом колесе на аналогичный показатель ведущей шестерни. Число больше 1 означает повышающую передачу, увеличивающую количество оборотов, скорость. Если меньше 1, то передача понижающая, увеличивающая мощность, силу воздействия.

Общее определение

Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.

Передачи с крутящим моментом

В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки. Наиболее распространенные передачи:

Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудование для изменения скорости вращения рабочего узла, в автомобилях.

Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.

Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.

Переходной конструкцией является ременная зубчатая передача.

На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.

Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.

Характеристика зубчатой передачи

В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.

Модуль – размер между одинаковыми точками двух соседних зубьев.

Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.

Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.

Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.

Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает. Такие передачи называют понижающими.

Зачем нужна паразитка

При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:

Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.

Виды зубчатых соединений

Зубчатое зацепление может иметь различную форму зуба на деталях. Это зависит от исходной нагрузки и расположения осей сопрягаемых деталей. Различают виды зубчатых подвижных соединений:

Самое распространенное и простое в исполнении прямозубое зацепление. Наружная поверхность зуба цилиндрическая. Расположение осей шестерни и колеса параллельное. Зуб расположен под прямым углом к торцу детали.

Когда нет возможности увеличить ширину колеса, а надо передать большое усилие, зуб нарезают под углом и за счет этого увеличивают площадь соприкосновения. Расчет передаточного числа при этом не изменяется. Узел становится более компактным и мощным.

Недостаток косозубых зацеплений в дополнительной нагрузки на подшипники. Сила от давления ведущей детали действует перпендикулярно плоскости контакта. Кроме радиального, появляется осевое усилие.

Компенсировать напряжение вдоль оси и еще больше увеличить мощность позволяет шевронное соединение. Колесо и шестерня имеют 2 ряда косых зубьев, направленных в разные стороны. Передающее число рассчитывается аналогично прямозубому зацеплению по соотношению количества зубьев и диаметров. Шевронное зацепление сложное в исполнении. Оно ставится только на механизмах с очень большой нагрузкой.

В конической зубчатой передачи оси расположены под углом. Рабочий элемент нарезается по конической плоскости. Передаточное число таких пар может равняться 1, когда надо только изменить плоскость действия силы. Для увеличения мощности нарезается полукруглый зуб. Передающееся количество оборотов считается только по зубу, диаметр в основном используется при расчетах габаритов узла.

Винтовая передача имеет зуб, нарезанный под углом 45⁰. Это позволяет располагать оси рабочих элементов перпендикулярно в разных плоскостях.

У червячной передачи нет шестерни, ее заменяет червяк. Оси деталей не пересекаются. Они расположены перпендикулярно в пространстве, но разных плоскостях. Передаточное число пары определяется количеством заходов резьбы на червяке.

Кроме перечисленных производят и другие виды передач, но они встречаются крайне редко и к стандартным не относятся.

Многоступенчатые редукторы

Как подобрать нужное передаточное число. Двигатель обычно выдает несколько тысяч оборотов в минуту. На выходе – колесах автомобиля и шпинделе станка, такая скорость вращения приведет к аварии. Мощности исполняющего механизма не хватит, чтобы рабочий инструмент мог резать металл, а колеса сдвинули автомобиль. Одна пара зубчатого зацепления не сможет обеспечить требуемое понижение или ведомая деталь должна иметь огромные размеры.

Создается многоступенчатый узел с несколькими парами зацеплений. Передаточное число редуктора считается как произведение чисел каждой пары.

U_р – передаточное число редуктора;

Перед тем как подобрать передаточное число редуктора, надо определиться с количеством пар, направлением вращения выходного вала, и делать расчет в обратном порядке, исходя из максимально допустимых габаритов колес.

В многоступенчатом редукторе все зубчатые детали, находящиеся между ведущей шестерней на входе в редуктор и ведомым зубчатым венцом на выходном валу, называются промежуточными. Каждая отдельная пара имеет свое передающееся число, шестерню и колесо.

Редуктор и коробка скоростей

Любая коробка скоростей с зубчатым зацеплением является редуктором, но обратное утверждение неверно.

Коробка скоростей представляет собой редуктор с подвижным валом, на котором расположены шестерни разного размера. Смещаясь вдоль оси, он включает в работу то одну, то другую пару деталей. Изменение происходит за счет поочередного соединения различных шестерен и колес. Они отличаются диаметром и передающимся количеством оборотов. Это дает возможность изменять не только скорость, но и мощность.

Трансмиссия автомобиля

В машине поступательное движение поршня преобразуется во вращательное коленвала. Трансмиссия представляет собой сложный механизм с большим количеством различных узлов, взаимодействующих между собой. Ее назначение — передать вращение от двигателя на колеса и регулировка количества оборотов – скорости и мощности автомобиля.

В состав трансмиссии входит несколько редукторов. Это, прежде всего:

Коробка передач в кинематической схеме стоит сразу за коленвалом, изменяет скорость и направление вращения.

Посредством переключения – перемещения вала, шестерни на валу соединяются поочередно с разными колесами. При включении задней скорости, через паразитку меняется направление вращения, автомобиль в результате движется назад.

Дифференциал представляет собой конический редуктор с двумя выходными валами, расположенными в одной оси напротив друг друга. Они смотрят в разные стороны. Передаточное число редуктора – дифференциала небольшое, в пределах 2 единиц. Он меняет положение оси вращения и направление. Благодаря расположению конических зубчатых колес напротив друг друга, при зацеплении с одной шестерней они крутятся в одном направлении относительно положения оси автомобиля, и передают вращательный момент непосредственно на колеса. Дифференциал изменяет скорость и направление вращения ведомых коничек, а за ними и колес.

Как рассчитать передаточное число

Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.

Расчет без учета сопротивления

В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.

Где u₁₂ – передаточное число шестерни и колеса;

Z₂ и Z₁ – соответственно количество зубьев ведомого колеса и ведущей шестерни.

Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».

При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.

Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.

Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:

Способ расчета передаточного числа позволяет спроектировать редуктор с заранее заданными выходными значениями количества оборотов и теоретически найти передаточное отношение.

Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.

КПД зубчатой передачи

Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:

Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.

Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.

При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.

Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.

Передаточное отношение зубчатой передачи

Значение передаточного числа зубчатой передачи совпадает передаточным отношением. Величина угловой скорости и момента силы изменяется пропорционально диаметру, и соответственно количеству зубьев, но имеет обратное значение.

Чем больше количество зубьев, тем меньше угловая скорость и сила воздействия – мощность.

При схематическом изображении величины силы и перемещения шестерню и колесо можно представить в виде рычага с опорой в точке контакта зубьев и сторонами, равными диаметрам сопрягаемых деталей. При смещении на 1 зубец их крайние точки проходят одинаковое расстояние. Но угол поворота и крутящий момент на каждой детали разный.

Например, шестерня с 10 зубьями проворачивается на 36°. Одновременно с ней деталь с 30 зубцами смещается на 12°. Угловая скорость детали с меньшим диаметром значительно больше, в 3 раза. Одновременно и путь, который проходит точка на наружном диаметре имеет обратно пропорциональное отношение. На шестерне перемещение наружного диаметра меньше. Момент силы увеличивается обратно пропорционально соотношению перемещения.

Крутящий момент увеличивается вместе с радиусом детали. Он прямо пропорционален размеру плеча воздействия – длине воображаемого рычага.

Передаточное отношение показывает, насколько изменился момент силы при передаче его через зубчатое зацепление. Цифровое значение совпадает с переданным числом оборотов.

Передаточное отношение редуктора вычисляется по формуле:

где U₁₂ – передаточное отношение шестерни относительно колеса;

ω₁ и ω₂ – угловые скорости ведущего и ведомого элемента соединения;

Отношение угловых скоростей можно считать через число зубьев. При этом направление вращения не учитывается и все цифры с положительным знаком.

Зубчатая передача имеет самый высокий КПД и наименьшую защиту от перегруза – ломается элемент приложения силы, приходится делать новую дорогостоящую деталь со сложной технологией изготовления.

Источник