в чем преимущества вычислительного эксперимента

Вычислительный эксперимент

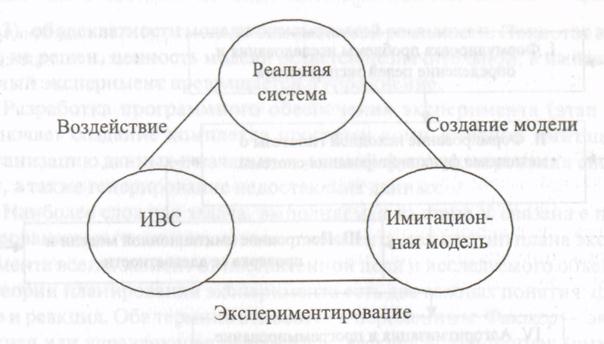
Принципиальное отличие вычислительного эксперимента от классического состоит в том, что он проводится не с реальной системой, а с ее моделью. В этом контексте особенно заслуживают внимания имитационные эксперименты. Под вычислительным экспериментом понимается численный метод проведения экспериментов с математическими и имитационными моделями, описывающими поведение сложных систем в некоторый период времени. В процессе вычислительного эксперимента исследователь имеет дело с тремя основными моделями (рис. 42):

1) реальным объектом (система);

2) имитационной моделью объекта;

3) информационно-вычислительной системой (ИВС).

В понятие «имитационная модель объекта» (или имитация) при вычислительном эксперименте вкладывается широкий смысл. Здесь понимается не только «чисто» имитационная модель, но и комплекс математических моделей, описывающих функционирование системы разной природы. Таким образом, вычислительный эксперимент — это всегда имитация некоторой реальности.

Область применения вычислительных экспериментов в экономике и управлении простирается от имитации конкретных видов деятельности до имитации функционирования корпорации и даже экономики страны с применением различного класса моделей. Об этом свидетельствуют исследования Т. Нейлора и его коллег из Университета социальных систем и имитационного моделирования, а также разработки в области моделирования экономики, управления и практического менеджмента — деловые игры, «case — stade» и практические управленческие задачи.

Рис. 4.1. Агрегированная структура вычислительного эксперимента

Вычислительные эксперименты позволяют исследовать все то, что не подвластно классическому эксперименту, а именно:

а) изучить сложные внутренние взаимодействия подсистем и эле­ментов системы и воздействие на их функционирование различного характера изменений во внешней среде;

в) получить новые знания, изучить и оценить новые ситуации, рас­полагая неполной информацией о событиях будущего;

г) проработать варианты стратегий и политики и предсказать узкие места и другие трудности до их фактического применения.

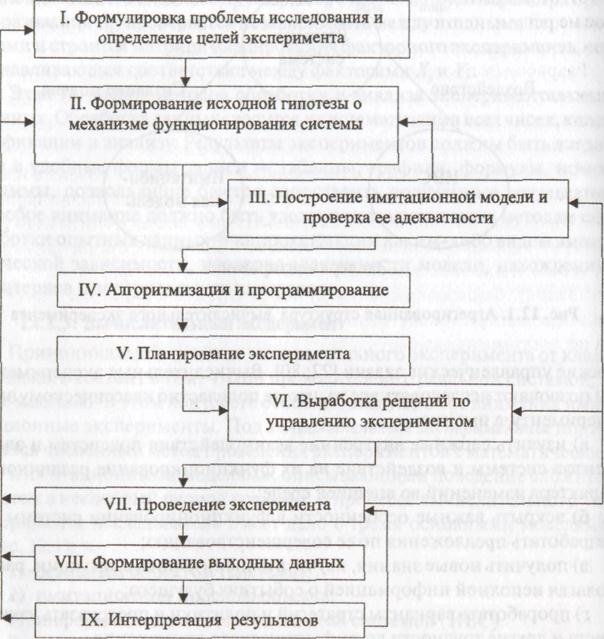
Схема основных этапов вычислительного эксперимента, составленная с учетом рекомендаций из публикаций, приводится на рис. 43.

Дадим краткое пояснение выделенным на рис. 43 этапам вычислительного эксперимента. Как и любое исследование, вычислительный эксперимент начинается с формулировки проблемы (этап I) и ясного изложения целей эксперимента. Цели эксперимента задают в виде:

• рабочих гипотез, которые надо проверить;

• вопросов, на которые надо ответить;

• управляющих воздействий, которые надо оценить.

Построению базовой модели всегда предшествует принятие гипотезы об особенностях функционирования исследуемой системы (этап II), например она динамическая или статическая, детерминированная или вероятностная, характер ее функционирования непрерывный или дискретный и т.д.

При построении имитационной модели системы (этап III) возникает несколько проблемных вопросов:

1) о сложности модели — надо строить такие математические мо­дели, которые давали бы точное описание поведения системы и не тре­бовали бы сложного программирования и вычисления;

2) о продолжительности программирования и вычислений на компьютере — эксперимент должен проходить за приемлемое для исследователя время;

3) об адекватности модели описываемой реальности. Пока этот вопрос не решен, ценность модели остается незначительной, а имитационный эксперимент превращается в упражнение.

Разработка программного обеспечения эксперимента (этап IV) включает создание комплекса программ компьютерной имитации, организацию данных и начальных условий функционирования системы, а также генерирование недостающих данных.

Наиболее сложная задача, выполняемая на этапе V, связана с планированием вычислительного эксперимента, так как тип плана эксперимента всегда зависит от поставленной цели и исследуемого объекта.

Рис. 4.2. Содержание и последовательность этапов

В теории планирования эксперимента есть два важных понятия: фактор и реакция. Оба термина относятся к переменным. Фактор — экзогенная или управляющая переменная, реакция — эндогенная (выходная) переменная. Анализ факторов при выполнении вычислительных экспериментов производится по следующей общепринятой схеме.

1. Управляем ли рассматриваемый фактор?

2. Наблюдаемы ли (измеряются, регистрируются, фиксируются) значения фактора?

3. Составляет ли влияние фактора предмет изучения или он включен только для увеличения точности эксперимента?

4. Являются ли уровни фактора количественными или качественными?

5. Является ли фактор фиксированным или случайным?

Планирование вычислительного эксперимента проводится с целью сокращения числа вычислительных прогонов и их продолжительности, количества наблюдаемых переменных, шагов изменения параметров и т.д. Не исключаются случаи, когда исследователь отказывается строго фиксировать схему проведения эксперимента. Принимаемая им стратегия предусматривает возможность принятия решений в зависимости от результатов, получаемых на отдельных этапах исследования. Например, исследователь, в зависимости от априорных сведений и ранее полученных результатов, прибегает последовательно к различным методам нахождения решения: линейному приближению, описанию полиномами второго, а иногда и третьего порядка и т.д. Здесь каждый последующий шаг определяется ранее полученными результатами. Планирование вычислительного эксперимента сопровождается рядом таких проблем, как «проблема объема» или проблема слишком большого количества факторов, проблема выбора плана эксперимента в соответствии с его целью, проблема многокомпонентной реакции, порождающая проблему оценки результатов имитационного моделирования. Планирование вычислительного, как и любого другого, экс­перимента заслуживает специального изучения.

Выработка решений по управлению экспериментом (этап VI) основана на оценке исходной гипотезы о поведении исследуемой системы и отладке имитационной модели и построении алгоритма (блок-схемы) организации эксперимента.

Имитационный эксперимент (этап VII) — это проведение серии имитационных расчетов в системном масштабе времени и по разработанному алгоритму. Каждая реализация модели отличается от другой только в одном изучаемом аспекте. Таким образом, в результате имитационного эксперимента образуются ряды статистических данных (выборки), обработка которых требует определенных знаний.

После того как эксперимент проведен и получены результаты, возникает задача — представить эти результаты в компактной форме, выдать рекомендации и сделать заключение (этапы VIII и IX). Основным требованием к обработке (редукции) выходных данных служит извлечение максимума информации. К основным методам обработки данных относятся методы математической статистики: дисперсионный анализ (критерий F, методы множественных сравнений упорядочения), спектральный анализ и эвристические процедуры, основанные на оценке параметров статистических распределений. Применение идей и методов математической статистики резко сокращает объем экспериментальных исследований и, что самое главное, увеличивает четкость суждений исследователя о полученных результатах в ходе эксперимента.

Каждый рассмотренный этап классического и вычислительного экспериментов — это этап исследования, требующий от исполнителя специальных знаний, больших затрат интеллектуальных и временных ресурсов.

Источник

Вычислительный эксперимент: способы и этапы проведения

Что это?

Для начала приведем актуальные для научного мира определения вычислительного эксперимента:

Использование вычислительных экспериментов связано с изучением таких процессов, лабораторное или натурное исследование которых было затруднено или вовсе невозможно. Например, в 40-50-е годы прошлого века советский академик Келдыш М. В. разработал математическое описание полетов в космос.

Отличительные характеристики метода

Вычислительные эксперименты позволяют узнать то, что не подвластно классическим (лабораторной и натурной) методикам:

Лабораторный и натурный эксперименты

Чем же они отличны от моделирования, вычислительного эксперимента? Разницу можно осознать, ознакомившись с определениями:

Ключевые преимущества метода

Перечислим главные достоинства вычислительного эксперимента перед другими методиками:

Методы эксперимента

Перечислим основные методы вычислительного эксперимента:

Этапы

Проведение вычислительного эксперимента, как и любого другого исследования, начинается с постановки целей последующей работы:

А теперь предлагаем вам подробно разобрать каждый из этапов исследования.

Первый этап

Здесь первой главной задачей для ученого становится выбор из всего многообразия свойств объекта исследования тех, которые действительно необходимо изучить во время проведения эксперимента.

Далее для исследуемого процесса обязательно строится вычислительная (математическая) модель. Она создается так, что способна разделять все факторы, влияющие на объект эксперимента, на две группы:

Затем обязательно сформировать рамки применимости модели, до которых считаются справедливыми полученные результаты.

Второй этап

Третий этап

На этом шаге компьютерного вычислительного эксперимента создается программа, позволяющая реализовать составленный алгоритм. Это этап программирования для электронно-вычислительных устройств.

Фактически здесь создается проект подготовки кода, составленного на языке высокого уровня. Он будет реализацией алгоритма численного решения задач.

Здесь перед учеными возникают следующие проблемные вопросы:

Четвертый этап

На этой ступени проводятся расчеты непосредственно на ЭВМ. Надо сказать, данный этап во многом напоминает осуществление лабораторного эксперимента. Различие лишь одно: если в лаборатории ученые с помощью специально созданной установки задают свои вопросы природе, то здесь при помощи ЭВМ вопросы задаются уже математической модели.

Пятый этап

Вот мы и подошли к завершению вычислительного эксперимента. Здесь важно получить результаты расчета, представленные некоторой цифровой информацией, которая в дальнейшем нуждается в расшифровке.

Ученые переходят к проведению расчетов и анализу полученных результатов. Это требует не только значительных интеллектуальных усилий, но и достаточных навыков по представлению, обработке и переосмыслению имеющихся выводов:

Источник

В чем преимущества вычислительного эксперимента

Конфигурационные построения, разбиравшиеся в предшествующих главах, могут использоваться практически всюду, где требуется разработка достаточно сложных программ. Область применения вариантного программирования, о котором пойдет речь в данной главе, также весьма широка. (Достаточно вспомнить вариантные фрагменты, настраивающие приложение на ту или иную вычислительную платформу, — с ними, вероятно, многим доводилось иметь дело.) Но относительный вес манипуляций над вариантами в общем объеме работ зачастую оказывается не таким уж заметным, из-за чего потребности в рациональном их оформлении отодвигаются на задний план.
Существует, однако, важный класс задач, для которого эффективное обеспечение многовариантности совершенно необходимо, более того, оно превращается в центральную проблему организации программирования. Этот класс задач — вычислительный эксперимент.

4.1. Вычислительный эксперимент

Вычислительный эксперимент — метод изучения устройств или физических процессов с помощью математического моделирования. Он предполагает, что вслед за построением математической модели проводится ее численное исследование, позволяющее «проиграть» поведение исследуемого объекта в различных условиях или в различных модификациях [Самарский, 1979; Горбунов-Посадов, 1990].
Численное исследование модели дает возможность определять разнообразные характеристики процессов, оптимизировать конструкции или режимы функционирования проектируемых устройств. Более того, случается, что в ходе вычислительного эксперимента исследователь неожиданно открывает новые процессы и свойства, о которых ему ранее ничего не было известно.

4.1.1. Сфера применения. Вычислительный эксперимент занимает промежуточное положение между натурным экспериментом и аналитическим исследованием.
Натурный (физический) эксперимент при надлежащей постановке может, вообще говоря, дать исчерпывающие и надежные результаты. И все же во многих случаях предпочтение отдается вычислительному эксперименту.
Дело в том, что в вычислительном эксперименте в роли опытной установки выступает не конкретное физическое устройство, а программа. Ее построение и последующие модификации, как правило, требуют существенно меньших затрат, чем подобные манипуляции над реальным объектом.
Кроме того, в опытной установке нередко просто невозможно бывает воссоздать некоторые критические режимы или экстремальные условия. Поэтому математическое моделирование может оказаться практически единственно возможным способом исследования.
При аналитическом подходе так же, как и в вычислительном эксперименте, строится математическая модель. Но исследуется эта модель исключительно посредством аналитических выкладок, без привлечения каких-либо численных методов. Если аналитических выкладок оказывается достаточно, то данный подход приводит к строгому точному решению.
Однако на практике, как это ни парадоксально, аналитическому подходу обычно отводится роль инструмента для (сравнительно быстрого) получения грубых оценок. Объясняется это тем, что аналитическими выкладками удается ограничиться только для несложных, сильно упрощенных моделей реальных процессов. Получаемое тут строгое аналитическое решение на самом деле в силу исходного огрубления модели оказывается весьма далеким от совершенства. Напротив, численные методы, применяемые в вычислительном эксперименте, дают возможность изучать более сложные модели, достаточно полно и точно отражающие исследуемые процессы.
Отмеченные достоинства вычислительного эксперимента вывели его в число основных методов исследования таких крупных физических и инженерно-технических проблем, как задачи ядерной энергетики, освоения космического пространства и др. Программные комплексы, обслуживающие вычислительный эксперимент, объемны и сложны, в их создание вовлечен многочисленный отряд программистов. Поэтому особую актуальность приобретает изучение возникающих здесь конфигурационных построений, которые, как будет видно из дальнейшего изложения, постоянно находятся в центре внимания участников такого рода разработок.

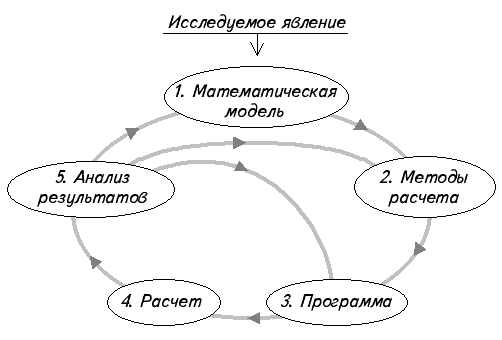
4.1.2. Цикл вычислительного эксперимента. В цикле вычислительного эксперимента можно выделить следующие этапы (рис. 4.1).

Рис. 4.1. Этапы вычислительного эксперимента

Э т а п 1. Построение математической модели (составление уравнений, описывающих исследуемое явление).
Э т а п 2. Выбор численных методов расчета (построение дискретной модели, аппроксимирующей исходную математическую задачу, построение разностной схемы, разработка вычислительного алгоритма и т. д.).
Э т а п 3. Создание программы, реализующей вычислительный алгоритм.
Э т а п 4. Проведение расчетов и обработка полученной информации.
Э т а п 5. Анализ результатов расчетов, сравнение (если это возможно) с натурным экспериментом.

Обычно на последнем (5-м) этапе исследователь приходит к заключению о том, что необходимо внести определенные изменения в решения, принятые на этапах 1, 2 или 3.
Так, может выясниться, что построенная модель недостаточно хорошо отражает особенности исследуемого явления. В этом случае модель корректируется, вносятся соответствующие поправки в численные методы и реализующие их программы и выполняется новый расчет. Тем самым цикл вычислительного эксперимента воспроизводится в полном объеме.
При анализе результатов могут быть выявлены какие-либо недостатки используемых численных методов, связанные, в частности, с соображениями точности или эффективности. Изменение методов влечет за собой изменение соответствующих программ и т. д. Иначе говоря, цикл повторяется в несколько сокращенном виде (этапы 2–5).
Наконец, может оказаться неудачным некоторое программное решение, например выбранный способ работы с внешней памятью. Пересмотр таких решений приводит к повторению этапов 3–5.

4.1.3. Особенности программирования. Разумеется, циклы, подобные циклу вычислительного эксперимента, возникают практически в любом мало-мальски сложном программном проекте. Самая первая версия программы обычно чем-нибудь не удовлетворяет разработчика или заказчика, и приходится уточнять постановку задачи, улучшать отдельные алгоритмы и т. д. Однако в большинстве случаев достаточно бывает выполнить несколько циклов, требующих сравнительно небольших усилий, и программа обретает желаемый вид.
Совершенно иначе обстоит дело в вычислительном эксперименте. Здесь программа мыслится как экспериментальная установка, от первых опытов с которой вряд ли следует ожидать сколько-нибудь интересных результатов. Данные первых опытов послужат всего-навсего отправной точкой длительного процесса изменений и усовершенствований установки, который только и способен привести к достаточно обоснованным заключениям об исследуемом объекте.
Таким образом, появление первоначальной версии программы лишь в самых общих чертах намечает направление исследований. Основная же работа по программированию еще впереди — она связана с многократными модификациями программы, отражающими эволюцию математической модели и методов ее расчета. Число циклов вычислительного эксперимента, каждый из которых сопряжен с модификацией расчетной программы, нередко достигает десятков тысяч. Поэтому рациональная организация таких модификаций — ключ к эффективному программированию данного класса задач.
Продолжая параллель с натурным экспериментом, можно заметить, что там обычно не спешат выбрасывать на свалку отдельные узлы, изъятые или замененные в экспериментальной установке при проведении очередного опыта: они еще не раз могут пригодиться впоследствии. Аналогично и решения (а вместе с ними и соответствующие им фрагменты программ), пересматриваемые на очередном цикле вычислительного эксперимента, как правило, не отбрасываются и могут использоваться затем для других расчетов. Например, метод, оказавшийся непригодным для одной модели, вполне может подойти для расчета следующей модели и т. д.
Итак, главное направление деятельности программиста, занятого вычислительным экспериментом, — не создание новых, а развитие существующих программ. Это развитие осуществляется, как правило, не за счет замены имеющихся модулей их более совершенными версиями, а за счет расширения: включения в программный фонд все новых и новых модулей, отражающих различные решения, принимаемые в ходе эксперимента.
Накапливаемые модули могут затем комбинироваться в самых разнообразных сочетаниях, позволяя тем самым провести достаточно систематическое и глубокое исследование. Потребность в подобных манипуляциях над модулями регулярно возникает в связи с тем, что исследователь постоянно конструирует новые варианты модели, сочетающие в себе те или иные выполнявшиеся когда-либо изменения или уточнения. Таким образом, интересующая нас многовариантность программ вычислительного эксперимента является закономерным следствием изначальной многовариантности модели.
Сложность реализуемых математических моделей, а также необходимость хранения многочисленных вариантных модулей приводят к тому, что характерные размеры программного фонда вычислительного эксперимента оказываются довольно внушительными. Число участвующих в расчетах модулей здесь нередко достигает нескольких тысяч, а суммарная длина текстов программ — сотен тысяч строк.
Организовать эффективное функционирование и развитие столь обширного, сложного и специфичного программного хозяйства очень нелегко. Тем не менее жизнь показала, что все возникающие здесь трудности вполне преодолимы — методом вычислительного эксперимента были успешно решены многие важные практические задачи. История программирования задач вычислительного эксперимента насчитывает свыше трех десятилетий, и за это время накоплен весьма значительный опыт, позволяющий говорить о существовании определенной технологии работы с многовариантными программами. Эта технология оказалась достаточно надежной и эффективной; именно добротностью применявшейся технологии объясняется жизнестойкость известных программных реализаций вычислительного эксперимента.
В задачах вычислительного эксперимента в полной мере проявляются практически все специфические особенности многовариантных программ. В то же время вычислительный эксперимент является наиболее крупным потребителем технологии многовариантности. Поэтому выражения «программирование задач вычислительного эксперимента» и «создание многовариантных программ» иногда будут использоваться как синонимы.

Источник

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ И ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ КАК НОВАЯ ФОРМА НАУЧНОГО ПОЗНАНИЯ

Компьютерное моделирование – один из прогрессивных методов научного исследования, который можно применить в различных сферах деятельности (промышленность, экономика, производство, образование и т.д.).

Вычислительный эксперимент позволяет заменить дорогостоящий натурный эксперимент расчетами на ЭВМ. Он позволяет в короткие сроки и без значительных материальных затрат осуществить исследование большого числа вариантов проектируемого объекта или процесса для различных режимов его эксплуатации, что значительно сокращает сроки разработки сложных систем и их внедрение в производство. Прибором эксперимента здесь является компьютер. Это процедура часто отождествляется с компьютерным моделированием.

Компьютерное моделирование и вычислительный эксперимент как новый метод научного исследования заставляет совершенствовать математический аппарат, используемый при построении математических моделей, позволяет, используя математические методы, уточнять, усложнять математические модели. Наиболее перспективным для проведения вычислительного эксперимента является его использование для решения крупных научно-технических и социально-экономических проблем современности (проектирование реакторов для атомных электростанций, проектирование плотин и гидроэлектростанций, магнитогидродинамических преобразователей энергии, и в области экономики – составление сбалансированного плана для отрасли, региона, для страны и др.). В некоторых процессах, где натурный эксперимент опасен для жизни и здоровья людей, вычислительный эксперимент является единственно возможным (термоядерный синтез, освоение космического пространства, проектирование и исследование химических и других производств).

Многие пользователи, искренне желая применить компьютерное моделирование в своей практической деятельности, сталкиваются с серьезными трудностями при освоении и использовании современных программных средств. Для работы с ними все еще требуются знания, не относящиеся непосредственно к моделированию, а проведение вычислительного эксперимента остается кропотливой и многотрудной работой. В то же время типовых задач моделирования не так уж и много, и для них можно создать удобный и понятный интерфейс в рамках одного, «универсального» пакета.

Создание прототипа универсального пакета из стандартных модулей, ориентированного на пользователя, не являющегося специалистом в области программирования и численного моделирования, приведет к тому, что компьютерное моделирование действительно станет инструментом научного работника, инженера и преподавателя.

Программные средства для моделирования можно разделить на две группы.

К первой отнесем пакеты, предназначенные для решения сложных промышленных и научно-исследовательских задач большими производственными или научными коллективами. Пакеты первой группы условно назовем промышленными. Такие проекты невозможны без предварительных исследований, выполняемых отдельными учеными или проектировщиками. Стартовой точкой в них является гипотеза, а основной задачей — ее проверка.

Промышленные пакеты слишком сложны и громоздки для проведения исследований на ранних стадиях и тем более обучения, для этого нужны специальные программные средства. Именно они, с нашей точки зрения, и образуют вторую группу пакетов. Назовем пакеты второй группы универсальными, подчеркивая этим, что они уступают по количеству уникальных возможностей промышленным, зато более просты для освоения и доступны отдельному исследователю при решении относительно несложных задач из практически любой прикладной области. Под несложными мы понимаем не простые задачи, а задачи, посильные одному разработчику, не являющемуся специалистом в области программирования и методов вычислений. В универсальных пакетах нужны разнообразные численные библиотеки, способные справиться с широким спектром проблем, а не методы, ориентированные на узкий класс задач. Для них нужны графические библиотеки, обеспечивающие показ изучаемого явления с разных сторон, а не одним, принятым в конкретной области, способом и, конечно же, поддержка интерактивного вмешательства в ход компьютерного эксперимента.

С момента появления пакета Simulink универсальные, не ориентированные на конкретные прикладные области пакеты для моделирования и исследования динамических систем в широком понимании этого термина, включая и дискретные, и непрерывные, и гибридные модели, стали повседневной реальностью. Относительная простота и интуитивная ясность входных языков универсальных пакетов в сочетании с разумными требованиями к мощности компьютеров позволяют использовать эти пакеты в учебном процессе. Изучаемые с помощью универсальных пакетов модели можно условно разделить на модели для естественнонаучных областей и модели технических объектов. В первом случае мы обычно имеем дело с моделью, сведенной к одной, итоговой системе уравнений, или, другими словами, с однокомпонентной моделью, а во втором — со структурированной, многокомпонентной моделью, итоговая система для которой должна строиться автоматически по описанию отдельных компонент.

И среди однокомпонентных, и среди многокомпонентных, наибольший интерес представляют модели, чье поведение меняется во времени в зависимости от наступающих событий. Их часто называют гибридными системами. В отечественной литературе также используются синонимы — непрерывно-дискретные, системы с переменной структурой, реактивные, событийно-управляемые.

Необходимость обеспечения обратной связи между исследователем и моделью опять же приводит нас к событийно-управляемым системам и дополнительно заставляет проводить и визуализировать вычислительный эксперимент в реальном времени. Назовем такой способ познания действительности активным компьютерным экспериментом, в отличие от традиционного пассивного вычислительного эксперимента, план которого может быть составлен заранее.

Отличительной чертой современных пакетов является объектно-ориентированный подход, позволяющий обеспечить еще одно очень важное и характерное для научных исследований и обучения требование — возможность легко пополнять и модифицировать разрабатываемую библиотеку, представляющую обычно последовательность все более сложных моделей, свойства которых приходится постоянно сравнивать.

Практически все существующие современные и широко используемые пакеты не приспособлены в полной мере для проведения активного вычислительного эксперимента.

Из всего множества современных пакетов моделирования, пакеты Model Vision Studium(MVS) [3], AnyLogic [4] наиболее приспособлены для проведения активных компьютерных экспериментов. Пакет AnyLogic разработанный фирмой «Экспериментальные объектные технологии» более мощная профессиональная система моделирования, которая для непрерывных и гибридных моделей использует решения апробированные в пакете Model Vision Studium, но является слишком сложным и дорогим. В силу этого и того, что разработчики пакета визуального моделирования MVS решили продолжать совершенствовать свой пакет, позиционируя его как компактный, несложный и недорогой инструмент для научных исследований и обучения, мы решили свой выбор остановить на пакете MVS. Кроме всего этого разработчики пакета визуального моделирования MVS объявили также об изменении политики его распространения. Вместо ограниченной бесплатной версии MVS Lite предлагается полноценная, свободная для некоммерческого использования версия MVS Free. Одновременно с экспериментальной версией будет продолжено распространение недорогой версии MVS Standard для отдельных преподавателей и университетов.

MVS использует современные объектно-ориентированные входные языки, используют гибридные автоматы как элементы входного языка, однако не может работать с неориентированными блоками. Пакет Model Vision Studium снабжен редактором трехмерной анимации (рис. 1), компактен и прост в освоении.

Достоинства гибридного автомата при использовании его в пакетах моделирования.:

· компактно и наглядно описывает всевозможные варианты смены поведения подобно тому, как конечный автомат столь же наглядно описывает все допустимые цепочки принимаемого им языка;

· требует указания в явном виде особых событий, приводящих к смене поведения, и облегчает работу численных методов в окрестности точки смены поведения;

· позволяет ввести «алгебру» локальных поведений, упрощая тем самым применение объектно-ориентированного подхода;

· позволяет легко описать сложные эксперименты с моделью, облегчая проектирование испытательных стендов;

· позволяет в наглядной форме следить за появлением событий, приводящих к смене поведения, и самими переключениями при отладке (рис.2).

Основным направлением развития пакета MVS является объектно-ориентированное моделирование непрерывно-дискретных систем с использованием формализма гибридного автомата. В ближайшее время предполагается внедрить в пакет «свободную» форму записи уравнений (с использованием производных произвольного порядка, а также уравнений, не разрешенных относительно производных), неориентированные блоки и связи, а также динамические структуры и графический язык управления экспериментом на основе карт состояния.

Главное окно пакета MVS Free 3.1

Литература

Колесов Ю. Б., Сениченков Ю. Б. Визуальное моделирование сложных динамических систем.— СПб.: Мир и семья и Интерлайн, 2000.— 240 с.

Бенькович Е. С., Колесов Ю. Б., Сениченков Ю. Б. Практическое моделирование сложных динамических систем.— СПб.: БХВ, 2001.— 441 с.

Колесов Ю. Б., Сениченков Ю. Б. Model Vision Studium — инструмент для объектно-ориентированного визуального моделирования сложных динамических систем // Труды Международ­ной научно-технической конференции: Гибрид­ные системы (7–9 июня, 2001).— СПб.— С. 5–46.

Колесов Ю. Б., Сениченков Ю. Компьютерное моделирование в научных исследованиях и в образовании// Компьютерные инструменты в образовании (№1(1)2003) – СПб.

Колесов Ю. Б., Сениченков Ю. Б. Компьютерное моделирование динамических систем // Научно-технические ведомости СПбГТУ.— 2002.— № 3.— С. 93–102.

Сениченков Ю. Б. CoLoS — новые методы в обучении. Опыт международного сотрудничества // Компьютерные инструменты в образовании.— 1999.— № 1.— С. 11–15.

Иванов В. Б. Опыт использования пакета MODELLUS при обучении физике и математике // Компьютерные инструменты в образовании.— 2000.— № 3–4.— С. 53–59.

Источник