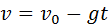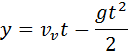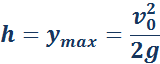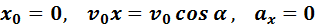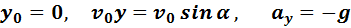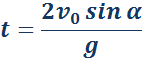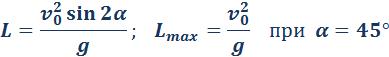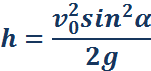в чем особенность свободного падения

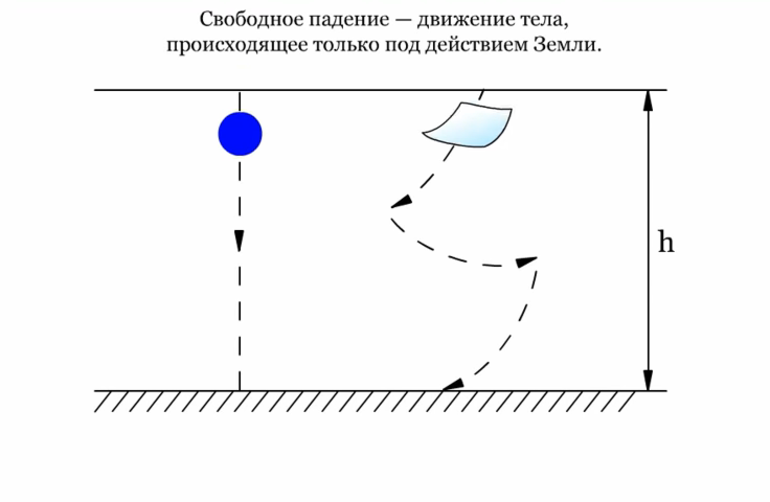
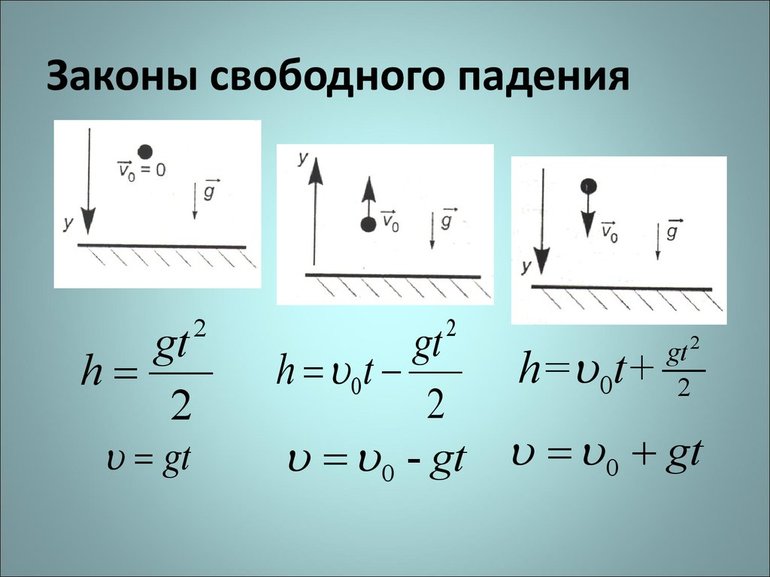
В чем особенность свободного падения

В условиях Земли падение тел считается условно свободным, т.к. при падении тела в воздушной среде всегда возникает еще и сила сопротивления воздуха.

Идеальное свободное падение возможно лишь в вакууме, где нет силы сопротивления воздуха, и независимо от массы, плотности и формы все тела падают одинаково быстро, т. е. в любой момент времени тела имеют одинаковые мгновенные скорости и ускорения.

Наблюдать идеальное свободное падение тел можно в трубке Ньютона, если с помощью насоса выкачать из неё воздух.

В дальнейших рассуждениях и при решении задачпренебрегаем силой трения о воздух и считаем падение тел в земных условиях идеально свободным.

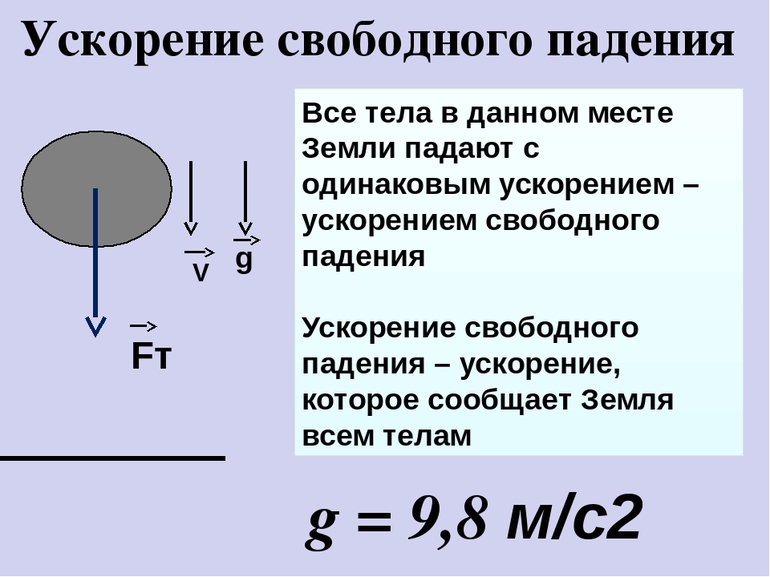
УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ

Ускорение свободного падения на Земле приблизительно равно :
g = 9,81м/с2.

Ускорение свободного падения всегда направлено к центру Земли.

Вектор силы тяжести и создаваемого ею ускорения свободного падения направлены всегда одинаково.

Все формулы для равноускоренного движения применимы для свободного падения тел.

Величина скорости при свободном падении тела в любой момент времени:

В этом случае вместо ускорения а, в формулы для равноускоренного движения вводится ускорение свободного падения g =9,8м/с2.

В условиях идеального падения падающие с одинаковой высоты тела достигают поверхности Земли, обладая одинаковыми скоростями и затрачивая на падение одинаковое время.

При идеальном свободном падении тело возвращается на Землю со скоростью, величина которой равна модулю начальной скорости.

Время падения тела равно времени движения вверх от момента броска до полной остановки в наивысшей точке полета.

Только на полюсах Земли тела падают строго по вертикали. Во всех остальных точках планеты траектория свободно падающего тела отклоняется к востоку за счет силы Кариолиса, возникающей во вращающихся системах (т.е. сказывается влияние вращения Земли вокруг своей оси).

Лишь итальянскому ученому Галилео Галилею удалось установить, что траекторией тела, брошенного под углом к горизонту в безвоздушном пространстве, является парабола.
А итальянец Тарталья (1500 – 1557г.), даже не зная законов движения, пришел к выводу, что наибольшей дальности стрельбы можно достичь, если наклонить орудие к горизонту под углом 45 градусов.

Минимальная скорость, которую достаточно сообщить брошенному вертикально вверх телу для того, чтобы оно не вернулось обратно, называют второй космической скоростью.

ЗАГЛЯНИ НА КНИЖНУЮ ПОЛКУ

А КАКОВО ПАДЕНИЕ ТЕЛ В РЕАЛЬНЫХ УСЛОВИЯХ?

Если выстрелить из ружья вертикально вверх, то, учитывая силу трения о воздух, свободно падающая с любой высоты пуля приобретет у земли скорость не более 40 м/с.

В реальных условиях из-за наличия силы трения о воздух механическая энергия тела частично переходит в тепловую. В результате максимальная высота подъема тела оказывается меньше, чем могла бы быть при движении в безвоздушном пространстве, а в любой точке траектории при спуске скорость оказывается меньшей, чем скорость на подъеме.

При наличии трения падающие тела имеют ускорение, равное g, только в начальный момент движения. По мере увеличения скорости ускорение уменьшается, движение тела стремится к равномерному.

Как ведут себя падающие тела в реальных условиях?

Возьмите небольшой диск из пластмассы, толстого картона или фанеры. Вырежьте из обычной бумаги диск такого же диаметра. Поднимите их, держа в разных руках, на одинаковую высоту и одновременно отпустите. Тяжелый диск упадет быстрее, чем легкий. На каждый диск действует при падении одновременно две силы: сила тяжести и сила сопротивления воздуха. В начале падения равнодействующая силы тяжести и силы сопротивления воздуха будет больше у тела с большей массой и ускорение более тяжелого тела будет больше. По мере увеличения скорости тела сила сопротивления воздуха увеличивается и постепенно сравнивается по величине с силой тяжести, падающие тела начинают двигаться равномерно, но с разной скоростью ( у более тяжелого тела скорость выше).
Аналогично движению падающего диска можно рассматривать движение падающего вниз парашютиста при прыжке с самолета с большой высоты.

Положите легкий бумажный диск на более тяжелый пластмассовый или фанерный, поднимите их на высоту и одновременно отпустите. В этом случае они будут падать одновременно. Здесь сопротивление воздуха действует только на тяжёлый нижний диск, а сила тяжести сообщает телам равные ускорения в независимости от их масс.

Если Землю просверлить насквозь и бросить туда камень, что будет с камнем?
Камень будет падать, набрав посередине пути максимальную скорость, дальше полетит по инерции и достигнет противоположной стороны Земли, причем его конечная скорость будет равна начальной. Ускорение свободного падения внутри Земли пропорционально расстоянию до центра Земли. Камень будет двигаться как груз на пружинке, по закону Гука. Если начальная скорость камня равна нулю, то период колебания камня в шахте равен периоду обращения спутника вблизи поверхности Земли, независимо от того, как прорыта прямая шахта: через центр Земли или по любой хорде.

Знаменитая «падающая» башня — это колокольня собора в городе Пизе, часть редкостного по своей красоте архитектурного ансамбля. Благодаря своему конструктивному изъяну она известна во всем мире. Башня достигает в высоту 55 метров, а надпись на ней свидетельствует, что заложена она в 1174 году. В 1564 году в Пизе родился Галилео Галилей, будущий знаменитый ученый. Судя по его собственным рассказам, он использовал Пизанскую башню для своих опытов. С верхнего ее этажа он бросал различные предметы, чтобы доказать, что скорость падения не зависит от веса падающего тела.

Источник

Свободное падение тел

Ускорение свободного падения

Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.

Ускорение свободного падения

Свободное падение тела

Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его.

Так как начальна скорость равна нулю, перепишем:

Отсюда находится выражение для времени падения тела с высоты h :

Движение тела, брошенного вертикально вверх

Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.

Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:

Максимальная высота подъема тела, брошенного вертикально:

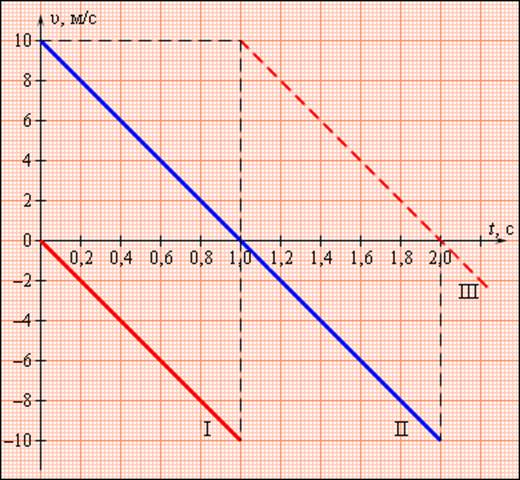
Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.

Движение тела, брошенного под углом к горизонту

С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.

Условия для движения вдоль оси О Х :

Условия для движения вдоль оси O Y :

Приведем формулы для движения тела, брошенного под углом к горизонту.

Дальность полета тела:

Максимальная высота подъема:

Источник

Общие сведения

Основоположником создания учения о движении стал Аристотель. Он утверждал, что скорость падения тела зависит от его веса. Значит, тяжёлый предмет сможет долететь до Земли быстрее, чем лёгкий. Если же на объект не будут воздействовать какие-либо силы, его движение невозможно.

Но Галилео Галилей, известный итальянский изобретатель и физик, изучая падение различных предметов и их инерцию, смог опровергнуть догадки Аристотеля. Результаты его исследований были революционными в науке. При этом даже была выпущена книга «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению», в которой были изложены основные размышления Галилея.

За дату рождения кинематики как науки можно принять 20 января 1700 года. В это время проходило заседание Академии наук, на котором Пьер Вариньона не только дал определения понятиям скорость, ускорение, но и описал их в дифференциальном виде. Уже после Ампер использовал для изучения процессов вариационное исчисление. Наглядные опыты провёл Лейбниц, а потом. профессор МГУ Н. А. Любимов смог продемонстрировать появление невесомости при свободном падении.

Под невесомостью понимают состояние тела, при котором силы взаимодействия с опорой, существующие из-за гравитационного притяжения, не оказывают никакого влияния. Такое положение имеет место, когда воздействующие на тело внешние силы можно охарактеризовать массовостью, например, тяготения.

В этом случае силы поля сообщают всем частицам предмета в любом из его положений равные по модулю и направлению ускорения, либо при движении возникают одинаковые по модулю скорости всех частиц тела. Например, поступательное движение. Состояние невесомости особо ярко проявляется в начальный момент при падении тела в атмосфере. Это связано с тем, что сопротивление воздуха ещё невелико.

Таким образом, для существования свободного падения нужно выполнение как минимум двух условий:

Что интересно, движение вверх тоже считается свободным падением, несмотря на обратное интуитивное восприятие, поэтому траектория движения может иметь форму как участка параболы, так и отрезка прямой. Например, камень, брошенный с небольшой высоты или поверхности под любым углом.

Опыт Галилея

Падение относится к реальному движению. Любое взаимодействие с Землёй приводит к изменению скорости из-за чего возникает ускорение. В 1553 году итальянец Джованни Бенедетти заявил, что 2 тела с разной массой, но одинаковой формы, брошенные в одной среде за одинаковое время пролетят равные расстояния. Это утверждение нуждалось в доказательстве, так как противоречило общепринятому на тот момент времени пониманию процессов. В частности, высказываниям Аристотеля.

Одним из экспериментаторов стал Галилей. Для проведения опыта учёному понадобилось:

Существует мнение, что вместо шара учёный использовал мушкетную пулю. Эксперимент заключался в следующем. Подняв 2 предмета на Пизанскую башню, Галилей сбросил их одновременно. Наблюдающие люди воочию смогли убедиться, что 2 тела упали на землю одновременно. Когда же один из учеников Аристотеля упрекнул итальянца, что на такой малой высоте невозможно оценить достоверно разницу, экспериментатор ответил: «Проделайте опыт самостоятельно, вы найдёте, что более тяжёлый предмет опередит тот, что легче на 2 пальца, поэтому, когда первый упадёт на землю, то второй будет от него на расстоянии толщины двух пальцев».

В своих работах Галилей рассуждал, что если связать верёвкой 2 тела разной тяжести, то с большим весом, по мнению Аристотеля, предмет будет лететь быстрее. Причём лёгкий объект начнёт замедлять падение тяжёлого. Но так как система в целом тяжелее, чем отдельно взятые тела, падать она должна быстрее самого тяжёлого тела. Другими словами, возникает противоречие, значит, предположение о влиянии веса на скорость падения неверно.

Сегодня эксперимент, подтверждающий доводы Галилея, может провести самостоятельно, пожалуй, каждый интересующийся. Такой опыт часто демонстрируют в средних классах общеобразовательной школы. Для этого нужно взять 2 трубки, длиной более метра и поместить в них 2 шарика разной массы. Затем создать внутри вакуум и одновременно их перевернуть. Если все условия соблюдены верно, то 2 тела опустятся на дно ёмкостей одновременно.

Если же опыт повторить не в вакууме, на шары будет действовать сила сопротивления, поэтому время падения уже не будет совпадать. Причём зависеть оно будет от формы предмета и его плотности.

Закон ускорения

Формула для свободного падения была выведена из выражения, определяющего силу тяжести: F = m * g. В соответствии с законом, падение предметов выполняется с одним и тем же ускорением вне зависимости от массы тела. По сути, это частный случай равноускоренного движения, обусловленное силой тяжести.

Для количественного анализа нужно ввести систему координат, взяв начало у поверхности Земли. Тогда можно рассмотреть падение тела массой m с высоты y0. Причём вращением планеты и сопротивлением воздушной среды нужно пренебречь.

Из полученных формул становится понятно, почему свободное падение не зависит от массы тела. При этом если начальная скорость будет равна нулю, то есть при падении предмету не сообщается импульс, текущее движение пропорционально времени, а пройденный путь определяется его квадратом.

Значения силы тяжести также зависит от строения земной коры и содержащихся в недрах полезных ископаемых. С учётом этого рассчитываются гравитационные аномалии: Δg = g — gср. Например, если g > gcp, то с большой вероятностью в земле содержатся залежи железной руды, в ином случае — нефти или газа.

Решение задач

Свободно двигаться, то есть не испытывать действие сторонних сил, могут любые тела в вакууме. Но в реальности на них оказывается воздействие как атмосферными явлениями, так и сопротивлением среды. При решении задач учитывается только сила тяжести, а вот остальными явлениями пренебрегают, считая их ничтожно малыми.

Вот некоторые из типовых задач, используемые при обучении в среднеобразовательных школах:

Тело вылетает вертикально вверх со скоростью 45 м/с. Какой высоты оно достигнет перед изменением направления полёта и сколько для этого понадобится времени. Для начала следует записать формулу скорости: v = v0 — gt. Отсюда можно рассчитать время полёта: t = v0 / g = 45 / 9,8 = 4,6 c. Теперь можно определить максимальную высоту: h = vot — (gt 2 / 2) = 45 м / с * 4,6 с — 9,8 м / с 2 * (4,6 c) 2 / 2 = 207 м — 103,7 м = 103,3 м.

Рассмотренные задания довольно простые. Но есть и повышенной сложности, требующие не только знания формул, но и умения выполнять анализ. Вот одно из таких.

Вертикальную составляющую можно вычислить, руководствуясь геометрическими принципами: v0y = v0 * sin (a). Учитывая, что h = (gt 2 / 2), для высоты горки можно записать: H = (g * (t 2 1 + t 2 2) / 2) — t1 * v0 sin (a). Так как gt1 = v0 sin (a), то рабочая формула примет вид: H = (g * (t 2 1 + t 2 2) / 2) — gt 2 1. После подстановки данных в ответе должна получиться высота равная 30 метров. Задача решена.

Источник

Свободное падение

1. Свободное падение — падение тел в безвоздушном пространстве под действием притяжения к Земле. Наблюдения свидетельствуют о том, что скорость свободно падающего тела увеличивается с течением времени. Поскольку на свободно падающее тело действует единственная сила — сила тяжести, то его ускорение постоянно, т.е. свободное падение — движение равноускоренное.

2. Опыт показывает, что все свободно падающие тела движутся с одинаковым ускорением. Так, если вертикально расположенную трубку, в которой находятся три тела, имеющие разную массу: пёрышко, кусочек пробки и дробинку, перевернуть, то эти тела будут падать на дно трубки. При этом, если в трубке есть воздух, то из-за сопротивления воздуха они упадут не одновременно: дробинка упадёт раньше всех, а пёрышко позже всех тел. Если же воздух из трубки откачать, то тела упадут на дно одновременно.

Ускорение свободного падения зависит от высоты тела над поверхностью Земли. Чем выше поднято тело, тем слабее оно притягивается к Земле, тем меньше ускорение свободного падения.

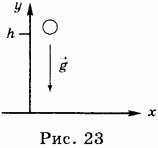
4. Уравнения зависимости от времени модуля скорости, пути и модуля перемещения свободно падающего тела с высоты ​ \( h \) ​ (рис. 23).

Уравнения зависимости от времени проекции скорости и координаты свободно падающего тела с некоторой высоты тела:

Знаки проекций зависят от направления оси координат и начала координат. В соответствии с рисунком

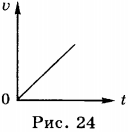
5. График зависимости модуля скорости от времени при свободном падении приведён на рисунке (рис. 24).

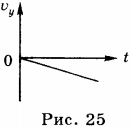
6. График зависимости проекции скорости от времени при свободном падении приведены на рисунке (ось Y направлена вертикально вверх) (рис. 25).

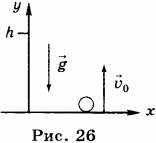
7. Тело, брошенное вертикально вверх, тоже движется равноускоренно с ускорением ​ \( g \) ​, которое направлено вертикально вниз. В этом случае, в отличие от свободного падения, скорость и ускорение движения направлены в противоположные стороны (рис. 26).

8. Уравнения зависимости от времени модуля скорости, пути и модуля перемещения тела, брошенного вертикально вверх с начальной скоростью ​ \( v_0 \) ​:​

\[ v=v_0-gt; l=v_0t-gt^2/2; s=v_0t-gt^2/2 \]

​Записанная формула зависимости пути от времени может быть использована только при движении тела в одну сторону (в данном случае вверх).

Уравнения зависимости от времени проекции скорости и координаты тела, брошенного вертикально вверх с начальной скоростью ​ \( v_0 \) ​ (ось Y направлена вертикально вверх): ​ \( v_y=v_<0y>+g_yt;y=y_0+v_<0y>t+g_yt^2/2 \) ​. Если тело брошено из начала координат, то ​ \( y_0=0 \) ​ и ​ \( y=v_0t-gt^2/2,v_y=v_0-gt \) ​.

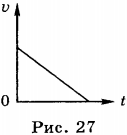
9. График зависимости модуля скорости от времени при движении тела вертикально вверх приведён на рисунке (рис. 27).

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Свободное падение — это

1) любое движение тела в безвоздушном пространстве
2) движение тела вертикально вверх в безвоздушном пространстве
3) падение тела в безвоздушном пространстве
4) падение тела в как безвоздушном пространстве, так и в воздухе

2. В трубке, из которой откачали воздух, одновременно с одной высоты начали падать три шарика: пенопластовый, пластилиновый и железный. Какой из шариков раньше коснется дна трубки?

1) пенопластовый
2) пластилиновый
3) железный
4) все шарики коснутся дна одновременно

3. Значение ускорения свободного падения зависит от

А. Массы тела.
Б. Широты местности.

Верными являются ответы:

1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б

4. Мяч падает с одинаковой высоты на поверхность Земли из состояния покоя на экваторе и на широте Москвы. В отсутствие сопротивления воздуха время падения мяча на экваторе

1) равно времени его падения на широте Москвы
2) больше времени его падения на широте Москвы
3) меньше времени его падения на широте Москвы
4) ответ может быть любым в зависимости от объёма

5. Мяч падает с одинаковой высоты на поверхность Земли из состояния покоя на экваторе и на широте Москвы. В отсутствие сопротивления воздуха скорость мяча у поверхности Земли на экваторе

1) равна его скорости на широте Москвы
2) больше его скорости на широте Москвы
3) меньше его скорости на широте Москвы
4) ответ может быть любым в зависимости от объёма

6. По какой формуле рассчитывается модуль скорости тела, брошенного вертикально вверх с поверхности Земли

1) ​ \( v=v_0+gt \) ​
2) \( v=v_0-gt \)
3) \( v=v_0+gt/2 \)
4) \( v=gt \)

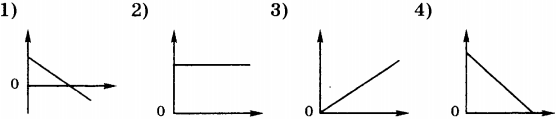
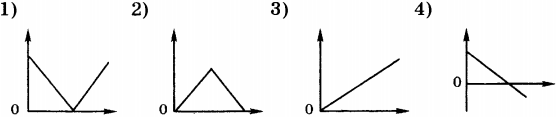
7. Какой из приведённых ниже графиков является графиком зависимости модуля скорости от времени свободного падения тела?

8. Какой из приведённых ниже графиков является графиком зависимости от времени проекции скорости тела, брошенного вертикально вверх, достигшего верхней точки и затем упавшего на Землю?

9. Чему равен модуль скорости свободно падающего тела через 4 с после начала падения?

1) 0,4 м/с
2) 4 м/с
3) 40 м/с
4) 160 м/с

10. На какую высоту поднимется тело, брошенное вверх со скоростью 20 м/с?

1) 20 м
2) 10 м
3) 2 м
4) 1 м

11. Тело, брошенное вертикально вверх, долетело до верхней точки и начало падать вниз. Установите соответствие между величиной, приведенной в левом столбце, и характером её изменения, приведенном в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА
A) модуль перемещения
Б) путь
B) координата относительно поверхности Земли

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется

1) ускорение движения первого тела больше ускорения движения второго тела
2) ускорение движения первого тела равно ускорению движения второго тела
3) скорость падения на Землю второго тела равна скорости падения на Землю первого тела
4) скорость падения на Землю второго тела больше скорости падения на Землю первого тела
5) тела упадут на Землю одновременно

Часть 2

13. Определите время и координату места встречи двух тел, одно из которых надает на землю с высоты 100 м, а другое тело брошено с поверхности Земли вертикально вверх со скоростью 25 м/с.

Источник

Свободное падение тел

Свободным падением тел называют падение тел на Землю в отсутствие сопротивления воздуха (в пустоте). В конце XVI века знаменитый итальянский ученый Г.Галилей опытным путем с доступной для того времени точностью установил, что в отсутствие сопротивления воздуха все тела падают на Землю равноускоренно, и что в данной точке Земли ускорение всех тел при падении одно и то же. До этого в течение почти двух тысяч лет, начиная с Аристотеля, в науке было принято считать, что тяжелые тела падают на Землю быстрее легких.

Простым примером свободного падения является падение тела с некоторой высоты h без начальной скорости. Свободное падение является прямолинейным движением с постоянным ускорением. Если направить координатную ось OY вертикально вверх, совместив начало координат с поверхностью Земли, то для анализа свободного падения без начальной скорости можно использовать формулу в 1.4, положив υ₀ = 0, y₀ = h, a = –g. Обратим внимание на то, что если тело при падении оказалось в точке с координатой y 0, a = –g. Это дает:

Через время υ₀ / g скорость тела υ обращается в нуль, т. е. тело достигает высшей точки подъема. Зависимость координаты y от времени t выражается формулой

Тело возвращается на землю (y = 0) через время 2υ₀ / g, следовательно, время подъема и время падения одинаковы. Во время падения на землю скорость тела равна –υ₀, т. е. тело падает на землю с такой же по модулю скоростью, с какой оно было брошено вверх.

Максимальная высота подъема

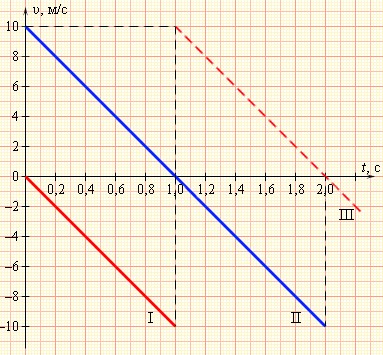
Графики скоростей для различных режимов движения тела с ускорением a = –g

На рис. 1.5.1 представлены графики скоростей для трех случаев движения тела с ускорением a = –g. График I соответствует случаю свободного падения тела без начальной скорости с некоторой высоты h. Падение происходило в течение времени t_п = 1 с. Из формул для свободного падения легко получить: h = 5 м (все числа в этих примерах округлены, ускорение свободного падения принято равным 10 м/с 2 ).

График II – случай движения тела, брошенного вертикально вверх с начальной скоростью υ₀ = 10 м/с. Максимальная высота подъема h = 5 м. Тело возвращается на землю через время t = 2 с.

График III – продолжение графика I. Свободно падающее тело при ударе о землю отскакивает (мячик), и его скорость за очень короткое время меняет знак на противоположный. Дальнейшее движение тела не отличается от случая II.

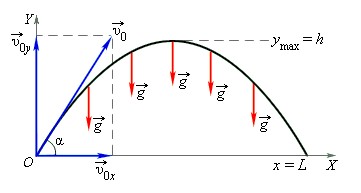
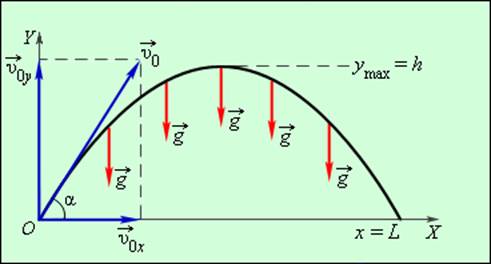
Задача о свободном падении тел тесно связана с задачей о движении тела, брошенного под некоторым углом к горизонту. Для кинематического описания движения тела удобно одну из осей системы координат (ось OY) направить вертикально вверх, а другую (ось OX) – расположить горизонтально. Тогда движение тела по криволинейной траектории можно представить как сумму двух движений, протекающих независимо друг от друга – движения с ускорением свободного падения вдоль оси OY и равномерного прямолинейного движения вдоль оси OX. На рис. 1.5.2 изображен вектор начальной скорости 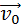тела и его проекции на координатные оси.

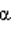
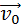
Движение тела, брошенного под углом к горизонту. Разложение вектора начальной скорости тела по координатным осям

Таким образом, для движения вдоль оси OX имеем следующие условия:

а для движения вдоль оси OY

Приведем здесь некоторые формулы, описывающие движение тела, брошенного под углом α к горизонту.

Время полета:

Дальность полета:

Максимальная высота подъема:

Движение тела, брошенного под углом к горизонту, происходит по параболической траектории. В реальных условиях такое движение может быть в значительной степени искажено из-за сопротивления воздуха, которое может во много раз уменьшить дальность полета тела.

Источник