в чем измеряются ставки
Что такое тарифная ставка
Все вопросы, касающиеся вознаграждения за выполненную работу, всегда живо волнуют и работодателя, и персонал. Ежемесячные выплаты могут иметь разный характер, состоять из разнородных компонентов и начисляться, исходя из отличающихся оснований. Рассмотрим понятие тарифной ставки, подробно проанализируем, как происходит ее расчет, а также проясним основные отличия между тарифной ставкой и окладом.
Что такое тарифная ставка
Люди не могут получать одинаковое вознаграждение за свою работу. Размер суммы, предназначенной к выплате в качестве зарплаты, зависит от:
Дифференциация зарплаты по степени выраженности этих пунктов выполняется в рамках тарифной системы трудового вознаграждения. Ключевым ее элементом является тарифная ставка как главная составляющая зарплаты.
Тарифная ставка – закрепленная документально величина финансового вознаграждения за достижение трудовой нормы той или иной степени трудности работником определенной квалификации за принятую единицу времени. Это «костяк», минимальная составляющая расчета за труд, на основании которой и строится сумма, получаемая сотрудниками «на руки».
СПРАВКА! Сумму, меньшую, нежели тарифная ставка, работник не может получать ни при каких обстоятельствах, если все функциональные обязанности им выполнены в полной мере, – это гарантированный законом минимум.
Не являются частью тарифной ставки:
Вопрос: В организации планируются организационные преобразования (кадровые перестановки, сокращение штата, изменение условий оплаты труда и т.д.). В каком случае потребуется внести изменения в штатное расписание и как часто их нужно вносить? Достаточно ли в трудовом договоре отразить только тарифную ставку (оклад), а поощрительные выплаты прописать в коллективном договоре?
Посмотреть ответ
Расчетное время тарифной ставки
Временным периодом, за который рассчитывается тарифная ставка, может быть любой удобный работодателю промежуток:
Часовые тарифные ставки удобно устанавливать, если на предприятии действует сменный график, обусловливающий режим суммированного учета рабочего времени, а также когда работают сотрудники-почасовики.
Дневные тарифные ставки применяются, когда работа имеет статус поденной, при этом количество рабочих часов в каждом таком дне одинаковое, но отличается от обычной нормы, установленной ТК РФ.
Месячные тарифные ставки действуют при постоянном соблюдении нормирования рабочего времени: стабильном графике, твердых выходных. В таких условиях работник «закроет» месяц независимо от того, сколько часов было отработано им по факту: отработав месячную норму, он зарабатывает свою ставку.
Функции тарифной ставки
Применение для начисления в денежной форме вознаграждения за выполнение трудовых функций – тарифная система оплаты – имеет ряд преимуществ перед другими формами оплаты.
Тарифная ставка как единица расчета заработной платы выполняет ряд важных функций:
ОБРАТИТЕ ВНИМАНИЕ! Главный принцип применения тарифных ставок – одинаковое вознаграждение за равную меру труда.
Как происходит расчет тарифной ставки
ВАЖНО! Образец трудового договора с указанием размера тарифной ставки от КонсультантПлюс доступен по ссылке
Единичной ставкой, с которой соотносятся все остальные разряды, является тарифная ставка 1 разряда – она определяет сумму, положенную сотруднику без квалификации за его работу в течение установленного временного промежутка.
Остальные разряды располагаются в зависимости от роста сложности работы и требуемой для нее квалификации (тарифные разряды), либо по уровню профподготовленности сотрудников (квалификационные разряды). Комплекс всех разрядов оставляет тарифную сетку предприятия. В ней каждый следующий разряд в несколько раз больше единичной ставки (то есть 1 разряда) – этот показатель отражает тарифный коэффициент.
К СВЕДЕНИЮ! МРОТ устанавливается государством, а все остальные элементы тарифной сетки принимаются отдельно для каждой организации и закрепляются в соответствующих локальных актах. Исключение – труд в организациях, финансируемых из государственного бюджета, где начисления происходят по Единой тарифной сетке (ЕТС).
Зная тарифный коэффициент и величину единичной ставки, всегда можно рассчитать полагающийся конкретному сотруднику размер выплаты согласно тарифу.
Пример расчета тарифа по ЕТС
На философский факультет государственного университета устраивается преподаватель, имеющий ученую степень кандидата философских наук и звание доцента. Он принят на должность доцента кафедры культурологии и назначен куратором студенческой группы. По Единой тарифной сетке, расчетный период которой равняется месяцу, его квалификация соответствует 15 разряду. Рассчитаем его заработную плату.
Минимальная оплата по ЕТС, соответствующая 1 разряду, равна значению МРОТ. Ее нужно умножить на тарифный коэффициент по 15 разряду тарифной сетки, а именно, 3,036.
В настоящее время на рассмотрении находится законопроект, регламентирующий порядок и размер полагающихся преподавательскому составу надбавок. Для нашего примера воспользуемся данными из этого законопроекта.
Для расчета тарифа нужно:
Пример расчета тарифа для почасовой ставки
Если сотрудник трудится по системе суммированного учета рабочего времени, то его тарифная ставка будет зависеть от часовой нормы на данный год – ее покажет производственный календарь, а также установленную на предприятии месячную тарифную ставку.
1 способ. Можно разделить на показатель ставки месячную норму по рабочим часам. Например, для рабочего определенной квалификации установлен тариф 25 000 руб. в месяц. При этом установленная норма рабочего времени на месяц составляет 150 часов. Таким образом, часовая тарифная ставка такого рабочего составит 25 000 / 150 = 166, 6 руб.
2 способ. Если нужно вычислить среднюю тарифную ставку почасовика в текущем году, сначала нужно определить среднечасовую месячную норму времени. Для этого соответствующий годовой показатель производственного календаря делим на 12 (количество месяцев). После этого уменьшаем в полученное количество раз среднемесячную тарифную ставку рабочего, установленную тарифной сеткой. Например, годовая норма составляет 1900 часов. Возьмем ту же месячную ставку, что и для предыдущего примера – 25 000 руб. Посчитаем, какую сумму в среднем зарабатывал в час этот рабочий в течение данного года: 25 000 / (1900 /12) = 157,9 руб.
Чем отличается тарифная ставка от оклада
Эти два понятия во многом схожи, так как оба они отображают денежное выражение трудового вознаграждения. Сейчас сходство между ними больше, чем несколько десятков лет назад, поскольку в трудовом праве происходят значительные изменения. Однако, имеются и существенные различия
Общие черты оклада и тарифной ставки
Различия тарифной ставки и должностного оклада
Сравним эти два понятия в следующей таблице.
Общие сведения о ПС
Таблица 1. Свойства процентной ставки
| Высокие процентные ставки | Низкие процентные ставки |
| Местная валюта становится более устойчивой | Местная валюта теряет свою устойчивость |
| Меньшая доходность для покупателей валюты за рубежом | Для зарубежных покупателей местная валюта становится более доступной |
| Увеличивается экономия | Увеличиваются расходы |
| Меньше доходов | Больше доходов |
| Выплаты по кредитам увеличиваются | Выплаты по кредитам уменьшаются |
| Больше процентов по депозитам | Меньше процентов по депозитам |
Сумма переплаты по простой процентной ставке = сумма кредита х годовая ПС х количество лет
Важно! Если вы оформили срочный кредит или займ, скорее всего, получите простую ПС.
Вся сумма = сумма кредита x (1 + процентная ставка / 100) лет
Важно! Сложные ПС используются для выплат по сберегательным и банковским вкладам, кредитным картам, автокредитам и ипотекам. Процент по кредитным картам может рассчитываться бесконечно долго, поэтому погашать задолженность по ним стоит как можно быстрее.
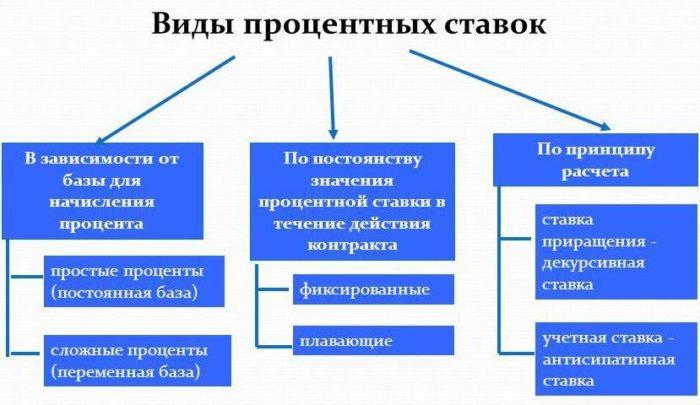
Виды процентных ставок
Фиксированные проценты
Важно! Банк всеми способами будет стараться удерживать вас в качестве должника. В большинстве случаев фиксированные ставки обычно выше, чем переменные, поскольку банки должны защитить себя. Если рыночные ставки внезапно увеличатся, ваши выплаты останутся неизменными, что для банка является убытком.
Переменные процентные ставки
Важно! Переменные ставки не всегда доступны для личных займов, но их использование с ипотекой является гораздо более распространенным явлением.
Чему равен 1 пункт (pips, point) на Forex и как его рассчитать
Добавлено в закладки: 0

На графике любого тренда валютной пары или самой валюты можно наглядно посмотреть на пункты и как они изменяются. Например, на валютной паре EUR/USD, стоимость которого изначально была 1.3600, а затем стала 1.3601 – смена цены произошла на 1 пункт. Трейдер в пунктах определяет свою прибыль, либо убыток.

Чтобы окончательно разобраться, что такое пункт на форексе, необходимо рассмотреть следующий пример: в утреннее время стоимость пары EUR/USD была на уровне 1.3705, а к вечеру доллар подешевел до курса 1.3755. Следовательно, в данной ситуации, можно говорить о том, что евро вырос на 50 пунктов. Если посмотреть те же изменения, но на валютной паре USD/JPY, стоимость которой была 85.55, а затем стала 85.00, то изменение курса произошло на 55 пунктов.
Большинство брокерских компаний (см. здесь наш рейтинг а здесь рейтинг брокерских компаний Форекс сайта http://ru.i-like-trading.com/) выдают четырехзначные расценки. Некоторые посредники используют пятизначные котировки, то есть после точки следует пять числовых знаков. Применение такого котирования в торговых условиях является наиболее точным и зачастую его используют при плавающем спрэде. Соответственно, один пункт при изменении цены при четырехзначном котировании будет равен 10 pips при использовании пятизначного котирования.
Особое внимание трейдерам следует обращать во время торговли. Когда он устанавливает стоп-или лимит-ордера, а также используя торговых роботов и другие индикаторы, чтобы не перепутать количество необходимых пунктов для закрытия позиции.
Как высчитать стоимость пункта при прямых котировках
Для правильной оценки цены пункта, чтобы сделка получилась прибыльная, необходимо научится самостоятельно рассчитывать соотношение размера лота и текущего курса.
Далее в примере, основой депозита будут использоваться доллары. Таким образом, необходимо вычислить стоимость одного пункта по этой валюте.

Например, в валютной паре USD/CHF текущее значение 1.2000. трейдеру необходимо рассчитать цену одного пипса для сделки равной 10000 (0.1 лот) основной валюты, т.е. доллара. Допустим текущий курс 10000USD=12000GHF. Далее соответствуя прогнозам трейдера, цена прошла в направлении вверх (либо вниз), изменилась на 1 пункт, и курс составил 1.2001. Теперь 10000 американских долларов уже будут стоить 12001 франков. Получается, что при изменение цены на один пункт трейдер заработал один швейцарский франк. Для более наглядного примера следует рассмотреть соотношение 1 к 1.2001. Получается 1/1.2001=0.83$. Получается цена пункта доллара 0.83.
Биржевые игроки пользуются следующей формулой для быстрых расчетов:
Цена pips=размер pips* объем позиции/текущий курс
Расчет стоимости пункта в обратной котировке
При расчетах стоимости пункта вобратнойрасценки валюты используется следующая формула:
Цена pips=размер pips*объем pips
На примере валютной пары EUR/USD можно увидеть расчет пункта в цифрах:
Стоимость одного пункта на форекс – автоматический расчет
Указанные выше формулы не обязательно запоминать, не нужно утруждать себя еще дополнительными самостоятельными вычислениями и расчетами. Ведь брокерские компании зачастую бесплатно предлагают современные торговые терминалы, которые автоматически сделают необходимые вычисления за трейдера. При установке ордеров игрок на бирже уже может увидеть автоматически просчитанную стоимость пункта, с учетом уже открытых сделок.
В MetaTrader для удобства участников международного рынка есть возможность видеть текущую прибыль, либо убыток, даже если в это время уже открыты позиции. После того, как трейдер закрывает позицию, то полученная прибыль автоматически фиксируется и пересчитывается в необходимую валюту.
Более того, у большинства брокерских компаний на сайте предоставлен специальный калькулятор для тех, кто не желает самостоятельно рассчитывать свою возможную прибыль по формулам. Единственное, трейдеру необходимо будет заполнить параметры, требуемые для заключения сделки (тип счета, размер кредитного рычага, депозита и лота). Далее с помощью выбранного калькулятора рассчитаются стоимость пункта, а также залог, спред и своп.
Любой начинающий трейдер может воспользоваться калькулятором на сайте брокера. Возможная прибыль покажется новичку очень легким способом заработка. Однако, не следует начинать торговлю на рынке без предварительного опыта на учебном счете. Здесь начинающий свою финансовую карьеру трейдер сможет на практике посмотреть зависимость прибыли от изменения валютного курса, а также сможет научиться самостоятельно рассчитывать стоимость пункта.
На видео: Как рассчитать лот вручную на Forex
Тема 1. Простые процентные и учетные ставки
Цель и задачи:
Цель и задачи изучения темы — ознакомить студентов с общими принципами и характеристиками финансовых расчетов, научить их грамотно проводить расчеты с простыми процентными и учетными ставками, реализовывать расчеты в Excel. Студенты должны определять результаты роста и дисконтирования, уметь выводить и корректно применять формулы перевода ставок из одних периодов времени в другие, знать и уметь использовать основные соотношения между результатами расчетов по простым процентным и учетным ставкам.
Оглавление
1.1. Характеристики доходности вложений
1.1.1. Текущее и будущее потребление
Доходы предприятия могут использоваться по различным направлениям. В общем случае часть доходов направляется на выплату дивидендов собственникам предприятия, владельцам акций, а другая часть инвестируется. Первая часть обеспечивает текущие потребности собственников, вторая часть служит для получения будущих доходов и обеспечивает отложенные потребности.
Инвестирование также предполагает различные направления. Часть средств может использоваться для расширения или модернизации производственных мощностей, часть — для совершенствования системы сбыта, часть — для повышения квалификации работников, часть — для совершенствования контроля качества и т. д.
Доходы физического лица, доходы человека также распределяются по различным направлениям. Часть своего дохода человек тратит на удовлетворение повседневных потребностей. Другая часть дохода представляет собой накопления. Она откладывается на будущее.
Этими деньгами можно распорядиться по-разному. Можно положить их на счет в тот или иной банк. Разные банки предоставляют свои услуги на различных условиях. Можно купить на эти деньги ценные бумаги, например государственные облигации или акции каких-либо предприятий. Можно вложить в конкретное дело, конкретный проект, рассчитывая на последующее участие в прибылях. Можно оплатить получение образования, рассчитывая на профессиональный рост в дальнейшем, и повышение доходов. Можно вложить деньги в пенсионный фонд в расчете обеспечить себе определенную пенсию через много лет. Можно приобрести страховой медицинский полис в расчете на получение в дальнейшем бесплатной медицинской помощи.
Возможны самые различные варианты вложений. Все эти варианты характеризуются тремя обстоятельствами.
Во-первых, предполагается отказ от текущего использование денежных средств в пользу будущего. Это означает, что момент вложения средств и момент получения результатов от вложения отделены друг от друга промежутком времени. Промежуток может быть коротким и измеряться несколькими днями или месяцами, например, если деньги даются в долг под проценты. Промежуток может быть длинным и измеряться годами и даже десятилетиями, если речь идет о вложениях в пенсионный фонд. Но в любом случае такой промежуток времени имеется. Момент вложения и момент получения результатов разнесены во времени.
Во-вторых, отказ от текущего потребления во имя будущего, отказ от сегодняшнего ради завтрашнего, должен окупаться. Другими словами, предполагается, что результаты вложений окажутся больше, чем вложенные средства. Увеличение вложенных средств — это и есть денежная оценка приносимой жертвы, денежная оценка отсрочки в потреблении. Поговорка «время — деньги» обретает в этой связи совершенно конкретный смысл. Разные варианты вложений могут дать разную денежную оценку одному и тому же промежутку времени, но в любом случае он получает некоторую денежную оценку, денежный эквивалент.
В-третьих, всякое вложение связано с риском. Иногда этот риск весьма мал. Так обстоит дело, например, с вложением в государственные ценные бумаги. Риск здесь связан с возможностью возникновения ситуации, когда государство не может выполнить свои финансовые обязательства. Такое может возникнуть при крахе государственных структур. В условиях политической и экономической стабильности вероятность такого краха можно считать близкой к нулю, риск вложений в государственные ценные бумаги практически отсутствует.
По-иному обстоит дело с негосударственными банковскими структурами. Здесь риск выше, причем для разных банков он различен. Еще более высокий риск обычно связан с вложениями в коммерческие предприятия.
Риск должен окупаться. Это означает, что ожидаемая прибыль рискованных вложений заметно выше обычной. Чем выше риск, тем выше должна быть эта прибыль. Если риск мал, то и прибыль будет не столь высокой. Поэтому обычно государственные ценные бумаги, являясь практически безрисковыми, дают малую прибыль. Ценные бумаги коммерческих структур, связанные со значительно более высоким риском, обещают и заметно более высокую прибыль.
Таким образом, расставаясь с частью своего дохода, предприятие или человек с определенной степенью уверенности рассчитывает вернуть через заданное время вложенные средства с вознаграждением, с прибылью.
1.1.2. Проценты и процентные ставки
В финансовых расчетах вознаграждение, получаемое в связи с вложением средств, носит название процента (или процентных денег). Под процентом понимается та сумма, измеряемая в денежных единицах, которую инвестор или вкладчик получает в виде прибыли, в виде вознаграждения.
Отношение этой прибыли к величине вложенных средств, выраженное в сотых долях, называется процентной ставкой (или ставкой процента).
При этом используют две формы выражения. Одну и ту же величину, например пятипроцентную, можно представить как 5 %, а можно как 0,05. В финансовых вычислениях следует использовать дробную форму записи. Именно в этой форме она будет в дальнейшем включаться в расчетные формулы.
Процент — это цена услуги, состоящей в отказе от использования денежных средств на текущее потребление в пользу предоставления этих средств в качестве ссуды.
Процентная ставка — это цена каждой денежной единицы (например, рубля) таких ссужаемых средств, цена каждой единицы такой услуги. Та или иная величина процентной ставки ориентирует на разное распределение средств между настоящим и будущим.
Процесс увеличения суммы вклада, связанный с присоединением процентов, называется наращением, или ростом, этой суммы.
Интервал времени, на который вкладываются денежные средства и за который выплачиваются проценты, называется периодом начисления.
Начисление процентов происходит, как правило, с определенной периодичностью (раз в год, квартал, месяц и т. п.). В таких случаях говорят о дискретных процентах. Иногда проценты начисляют каждый день, а в некоторых случаях и еще чаще. Тогда говорят о непрерывных процентах.
Во многих случаях экономический анализ, основывающийся на непрерывном начислении процентов, оказывается более простым и удобным, чем при предположении о дискретном начислении. Поэтому формулы для непрерывного начисления используют часто также и в тех случаях, когда проценты начисляются дискретно. Процентная ставка в финансовом анализе используется не только как измеритель доходности непосредственно денежных вложений, но и как измеритель эффективности самых различных финансовых, производственно-хозяйственных, коммерческих операций. Ее применяют и в тех случаях, когда непосредственное вложение денег в явном виде в операции не присутствует.
Существуют различные формы начисления и выплат процентных денег. Обычно эти деньги присоединяются к сумме вклада и выплачиваются по окончании периода начисления. В некоторых случаях проценты выплачиваются регулярно до окончания срока вклада (например, деньги вложены на год, а проценты начисляются и выплачиваются каждый месяц). Иногда проценты начисляют и выплачивают в начале операции. Вкладчику часть средств возвращается в виде процентов не в конце срока, а в его начале, в момент вклада. По сути дела, можно считать, что он вкладывает не всю оговоренную сумму средств, а сумму за вычетом процентов. В конце же срока он получит оговоренную сумму. В таких случаях часто ставку процента называют учетной ставкой.
Чем раньше вкладчик вернет свои средства или хотя бы их часть, тем раньше он сможет воспользоваться этими средствами (например, вложить их еще раз). При прочих равных обстоятельствах. Отказываясь от своих средств на длительный срок, вкладчик приносит большую жертву, чем при отказе на короткий срок. Заинтересовать вкладчика на длительный срок вклада труднее, чем на короткий. Поэтому обычно при длительных сроках процентная ставка предлагается большей, чем при коротких. При выплате процентов в конце, вместе с возвратом вклада, процентная ставка бывает выше, чем при выплатах по ходу срока вклада. Выплата процентов в начале срока наиболее выгодна вкладчику, поэтому учетная ставка обычно оказывается меньше других видов процентных ставок.
Ставка процента может применяться к одной и той же первоначальной сумме на протяжении всего срока вклада. В этом случае говорят о простых процентных ставках (простых процентах). Однако возможны и другие ситуации, когда ставка процента применяется не только к первоначальной сумме, но и к сумме процентных денег, начисленных ранее. В таком случае говорят о сложных процентных ставках (сложных процентах), или о капитализации процентов.
И для простых, и для сложных процентных ставок сама величина ставки на протяжении срока вклада обычно не изменяется, меняться может лишь сумма денег, к которым эта ставка применяется, и, соответственно, сумма выплачиваемых процентных денег. Однако в условиях договора могут использоваться и другие, переменные, плавающие варианты процентных ставок. Например, может быть оговорено, что процентная ставка должна на определенную величину превышать заранее неизвестный темп инфляции, складывающийся на протяжении срока договора. В этом случае величина процентной ставки заранее не известна, но она оказывается определенным образом привязана к изменяющемуся показателю инфляции.
1.1.3. Принятые обозначения
В дальнейшем анализе и формульных расчетах приняты стандартные обозначения:
P — начальная величина денежной суммы,
S — конечная величина денежной суммы,
i — процентная ставка,
t — срок вклада или ссуды.
В каждой конкретной формуле ставка i (или d) и время t предполагаются соразмерными. Это означает, что если, например, ставка годовая, то и время измеряется в годах, а если ставка месячная, то и время измеряется в месяцах.
Величина S называется наращенной величиной суммы P. Величина P называется современной (или приведенной) величиной суммы S.
Определение наращенной суммы S по начальной сумме P называют компаундингом. Обратную операцию, определение современной величины P будущей суммы S, называют дисконтированием.
Если речь идет о компаундинге, об определении наращенной суммы вклада, то разность S — P называют процентами, или процентными деньгами, и обозначают обычно посредством I:
I = S — P.
Если же речь идет о дисконтировании, об определении современной стоимости будущей суммы S, то та же разность S — P называется дисконтом и обозначается обычно посредством D:
D = S — P.
Отношение S/P, показывающее, во сколько раз наращенная сумма превышает первоначальную величину вклада, называют коэффициентом (или множителем) роста.
Отметим, что наряду с указанными обозначениями в литературе по финансовому менеджменту используются иногда и другие обозначения. Так, начальную величину денежной суммы P обозначают также двухбуквенным сочетанием PV ( Present Value), а конечную величину денежной суммы S обозначают иногда посредством FV ( Future Value).
1.1.4. Принцип финансовой эквивалентности
Ценность денежной суммы, меньшей по размеру, но полученной раньше по времени, может оказаться больше ценности другой суммы, большей по величине, но полученной позже. Денежные суммы, выплаты которых приурочены к различным моментам времени, непосредственно не соизмеримы друг с другом. Для их соизмерения следует пересчитать такие суммы к одному моменту времени. Пересчет, или приведение сумм к тому или иному моменту времени, осуществляется на основе процентной или учетной ставки.
Предположим, что получение суммы R1 приурочено к моменту времени t1, а получение суммы R2 — к моменту времени t2. Если эти два момента времени совпадают, то денежные суммы можно сравнивать непосредственно. Если же они не совпадают, то для сравнения следует перевести обе суммы к одному моменту времени.
Пусть, для определенности, момент t1 наступает раньше момента t2,
то ее ценность выше, чем ценность второй суммы, поскольку она не только раньше получена по времени, но и больше по величине. Однако если данное неравенство не выполнено, т. е. если
R1 
то результат сравнения не очевиден.
Для того чтобы эти суммы можно было сопоставить друг с другом, представим себе, что сумма R1 в момент t1 положена на банковский счет, где она растет по заранее определенной процентной ставке. Тогда к моменту t2 она превратится в некоторую сумму S, большую, чем R1. Сравнение величин R1 и R2, отнесенных к разным моментам времени, сводится к сравнению величин S и R2, отнесенных к одному и тому же моменту времени t2.
R1 имеет большую ценность, чем R2.
то R1 и R2 имеют одинаковую ценность. В этом случае суммы R1 и R2 считаются финансово эквивалентными (при данной процентной ставке).
Финансовая эквивалентность денежных сумм зависит от величины процентной ставки. При одной ставке две суммы могут оказаться эквивалентными, а при другой нет. Она может зависеть также от формы начисления процентов и некоторых других обстоятельств.
Однако общий принцип остается неизменным: для сравнения денежных величин, относящихся к разным моментам времени, следует пересчитать (привести) их к одному и тому же моменту времени.
1.2. Простые процентные ставки
1.2.1. Рост суммы при простой процентной ставке
Пусть P — первоначальная сумма вклада, S — конечная сумма (вместе с начисленными процентами). Тогда разность I между S и Р
I = S — P
определяет процент (процентные деньги) за весь срок вклада. Эта величина складывается, как мы видели на примере, из одинаковых частей. Каждая часть, каждое слагаемое соответствует своему году (своему периоду) вклада.
позволяет вычислить конечную сумму денег через ее начальную сумму Р и процентную ставку i при любом числе лет n. Более того, эта же формула годится и для нецелого числа лет. Например, для определения конечной суммы с процентами через полтора года вместо n следует подставить 1,5. Для определения этой суммы через 1 месяц вместо n следует подставить 1/12.
Общая формула для произвольного промежутка времени t (не обязательно состоящего из целого числа лет) имеет прежний вид:
Здесь вместо целочисленной величины n используется произвольная положительная величина t. Эта формула называется формулой простых процентов.
Сумма вклада S линейно растет во времени (рис. 1.1).
Графиком является прямая линия. Она начинается в точке P на вертикальной оси. Угол наклона прямой, т. е. крутизна роста, определяется произведением двух величин: начальной суммы вклада P и процентной ставки i. Чем больше каждая из этих величин, тем больший прирост получает вклад за единицу времени (например, за 1 год).
Рис. 1.1. График роста величины вклада
1.2.2. Простая переменная ставка и средние арифметические величины
Рассмотрим ситуацию с переменной простой процентной ставкой. Пусть на первом промежутке времени длиной t1 ставка равна i1, на втором промежутке длиной t2 ставка равна i2, на третьем промежутке длиной t3 ставка равна i3 и т. д. Первый промежуток начинается в момент 0 и заканчивается в момент t1, второй начинается в момент t1 и заканчивается в момент t1 + t2, третий начинается в t1 + t2 и заканчивается в t1 + t2 + t3 и т. д. Промежутки могут иметь различную длину. График роста по такой переменной ставке представляет собой ломаную линию (линейный сплайн — рис 1.2).
Рассмотрим n таких промежутков длиной t1, t2. tn. Величина вклада к концу последнего промежутка составит
При сравнении различных вариантов вложения денежных средств важно определить среднюю процентную ставку по вкладу.
Обозначим посредством T общий срок вклада по переменной ставке:
а посредством 

Средняя процентная ставка i по определению удовлетворяет следующему условию: если ее подставить в формулу роста вместо каждой из ставок ik, то результат расчета при этом не изменится. Таким образом,
Отсюда получаем формулу для средней простой процентной ставки i:
Согласно формуле, средняя процентная ставка i является средневзвешенной ставок ik, причем в качестве весовых коэффициентов выступают доли соответствующих промежутков времени в общем сроке вклада.
Весовые коэффициенты удовлетворяют естественному условию:
Процентные ставки для тех промежутков времени, которые имеют относительно большую длину, войдут в итоговую средневзвешенную величину с большим весом.
В частном случае, когда длины всех промежутков времени равны друг другу, доля каждого из них равна 1/n, и средневзвешенная величина переходит в обычную среднюю арифметическую:
Рис. 1.2. Рост по простой переменной ставке
1.2.3. Годовые, квартальные, месячные ставки процента
Если процентная ставка i определена для периода в 1 год (годовая ставка), то и при измерении промежутка времени t в качестве единицы измерения следует использовать год. В этом случае, например при промежутке времени в полтора года, вместо t следует подставить число 1,5. Если же процентная ставка i привязана к другому промежутку времени, скажем месяцу, то и промежуток времени t следует измерять месяцами. В этом случае при прежней длине промежутка в полтора года вместо t следует подставить число 18.
Годовая ставка и месячная ставка связаны друг с другом равенством:
Для получения квартальной ставки следует годовую ставку разделить на 4 или месячную умножить на 3.
При использовании квартальных ставок промежуток времени t измеряется в кварталах. Например, для полуторагодового промежутка t = 6.
1.2.4. Точные и обыкновенные процентные ставки
Обычно пользуются годовыми процентными ставками. Расчет процентных денег за определенное число дней при использовании годовой ставки i связан с некоторыми особенностями.
При точных расчетах следует считать, что год содержит 365 (или 366) дней. В этом случае говорят о точных процентах.
Однако часто при банковских расчетах считают, что год содержит 360 дней. промежуток времени стандартной длины. В этом случае говорят об обыкновенных процентах. Таким образом при расчетах используют две временные базы. К=365(366) дней и К=360дней. В зависимости от принятой методики расчета используют три метода.
1. Точные проценты с точным числом дней. Обозначается АСТ/365 или 365/365. Количество дней операции расчитывается точно по календарю. Первый и последний день принимаются за один. К= 365.
2. Обыкновенные проценты с точным числом дней.Обозначается АСТ/360. Количество дней операции расчитывается точно по календарю.Первый и последний день принимаются за один К=360.
3. Обыкновенные проценты с приближенным числом дней.Обозначается АСТ/360. Количество дней операции в каждом месяце принимается равным 30.Первый и последний день принимаются за один.К=360
Начисления с обыкновенными процентами с точным числом дней дают несколько больший результат, чем начисления с точными процентами.
Определим расхождения в расчетах по точным и обыкновенным процентам в общем случае. При расчете по точным процентам конечная сумма ST равна:
При расчете по обыкновенным процентам конечная сумма равна
Разность между ними составляет величину 
1.3. Простые учетные ставки
1.3.1. Учет и дисконтирование
Выше были приведены формулы, которые позволяют по начальной величине вклада P определить конечную сумму S. В финансовой практике часто возникает и обратная задача: по заданной конечной сумме S определить необходимую начальную величину Р. Такая задача возникает, например, при применении учетной ставки, когда проценты с суммы S удерживаются при выдаче кредита. Такая же задача возникает при получении платежных обязательств (векселей), расчет по которым будет производиться в будущем.
Операцию начисления и удержания процентов вперед называют учетом, а разность D
D = S — P,
называют дисконтом.
Мы видим, что дисконт D и процент I определяются одинаковыми формулами. Различие между ними в том, что процент выплачивается в конце, по окончании срока вклада (если договором не оговорена постепенная выплата процента по отдельным периодам срока). Дисконт же выплачивается в начале срока. Про величину S говорят при этом, что она дисконтируется.
Дисконтирование — это преобразование будущей величины стоимости в оценку этой величины для настоящего момента времени. Такое преобразование называют также приведением будущей стоимости к текущему моменту времени.
Дисконтирование используют не только в задачах, связанных с проведением той или иной конкретной финансовой операции (выдачей векселя, ссуды и т. п.). Оно имеет гораздо более широкий круг применения.
Дисконтирование как способ оценки будущей стоимости путем приведения ее к настоящему моменту времени позволяет ввести время в финансовые расчеты, дать денежную оценку времени.
В зависимости от целей дисконтирования используют две формулы расчета. Одна связана с математическим дисконтированием, другая — с банковским дисконтированием (учетом).
При расчетах по математическому дисконтированию (при простой процентной ставке) исходят из указанной выше формулы
Эта формула выражает конечную сумму S через начальную величину Р. Отсюда можно сразу получить выражение, определяющее начальную величину Р через конечную сумму S:
Величина 
При расчетах по схеме банковского учета (при простой учетной ставке) используют другую формулу, выражающую начальную величину Р через конечную сумму S:
Здесь дисконтным множителем является величина m
где d — учетная ставка.
Математическое дисконтирование точным и корректным образом связывает исходную и конечную величины P и S. Оно активно используется в теоретическом финансовом анализе. Однако на практике в коммерческих операциях при покупке векселей и других платежных обязательств часто используют другую схему — схему банковского учета. Связано это с тем, что в соответствии с последней схемой зависимость дисконтного множителя от времени более простая и наглядная.
Действительно, зависимость дисконтного множителя m от времени t при математическом дисконтировании графически представляется в виде смещенной ветви гиперболы (рис. 1.3).
Рис. 1.3. График зависимости дисконтного множителя
от времени при математическом дисконтировании
График же зависимости дисконтного множителя m от времени t при банковском учете представляет собой график убывающей линейной функции, прямую линию (рис. 1.4). Тангенс угла наклона этой прямой равен d, т. е. определяется учетной ставкой, взятой с противоположным знаком.
Рис. 1.4. График зависимости дисконтного множителя
от времени по схеме банковского учета
На графиках хорошо видно, что при математическом дисконтировании множитель, постепенно уменьшаясь, остается положительным. При банковском учете это не так. Дисконтный множитель обращается в 0 при t = 1/d, а затем становится отрицательным. Пользоваться такой формулой расчета можно лишь для промежутков времени t, меньших чем 1/d.
Эти два способа расчета дают различные результаты.Рассмотрим следующий пример. Заёмщику предоставлен кредит в 1 млн.руб.на 1год под ставку 10% годовых. Очевидно, что проценты для такой операции составят 100 тыс.руб.Рассмотрим два варианта выплаты процентов.
Если проценты выплачиваются в конце периода, то используется формула наращивания по процентной ставке:
Если проценты выплачиваются в начале периода в начале периода,то это фактически означает, что заёмщик получает 1млн.руб., с учетом процентов, т.е. 1 000 000-100 000=900 000руб., а в конце периода возвращает 1 млн.руб.Если теперь использовать приведеную выше формулу:
Указанное несоответствие преодолевается с использованием формулы наращивания по учетной ставке:
для того, чтобы получить результат 1 млн.руб. с использованием ставки наращения нужно увеличить значение ставки с 1/10 до 1/9 (примерно 11%)
При заключении финансового соглашения следует оговорить, какая схема расчета будет использоваться.
1.3.2. Срок кредита, процентные и учетные ставки
Приведенные выше формулы позволяют определить срок вклада, величину процентной или учетной ставки через остальные характеристики условий вклада. Эти же формулы могут быть использованы и для других финансовых операций, в том числе и при заключении договоров о ссудах, кредитах.
Для определения продолжительности кредита следует соответствующим образом преобразовать исходные формулы. Из формулы
определяющей характеристики кредита через процентную ставку i, получаем:
определяющей характеристики кредита через учетную ставку d, получаем:
В обеих расчетных схемах, и по процентной, и по учетной ставке, время кредита прямо пропорционально приращению средств (проценту или дисконту) и обратно пропорционально величине ставки (процентной или учетной).
Аналогичным образом можно выразить величину ставки через остальные характеристики кредита. Для процентной ставки i получим:
Для учетной ставки d получим:
1.3.3. Основные соотношения между процентными и учетными ставками
В рассмотренном выше примере 50% учетная ставка приводит к тем же финансовым результатам, что и 60% процентная ставка. Найдем соотношения между этими видами ставок в общем виде.
Для процентной ставки основная формула имеет вид:
Для учетной ставки основной формулой является
Подставив правую часть первой формулы вместо S во вторую, получим:
После сокращения обеих частей на Р и проведения простых преобразований получим:
Эти формулы позволяют по учетной ставке находить равносильную ей процентную ставку (дающую тот же финансовый результат) и, наоборот, по процентной ставке находить равносильную ей учетную.
Заметим, что в формулах присутствует длина интервала времени t. Отсюда следует, что равносильную ставку другого вида можно вычислить только в том случае, если указан интервал времени, на который рассчитана финансовая операция (в случае кредита указан срок, на который выдаются деньги). При изменении интервала времени величина равносильной ставки другого вида изменится.
Совпадение численных значений ставок двух видов, т. е. равенство
i = d,
могло бы иметь место только для такой операции, протяженность которой t равна 0, момент начала и окончания которой совпадают. Это непосредственно следует из полученных формул.
В случае кредитования это означало бы, что выдаваемый кредит тут же возвращается кредитору. Понятно, что такая операция не имеет смысла. Для реальных финансовых операций значения двух видов ставок расходятся, причем всегда процентная ставка выше равносильной ей учетной ставки:
i > d.
Выводы
Расставаясь с частью своего дохода, предприятие или человек с определенной степенью уверенности рассчитывает вернуть через какое-то время вложенные средства с вознаграждением, с прибылью.
В финансовых расчетах вознаграждение, получаемое в связи с вложением средств, носит название процента (или процентных денег). Под процентом понимается та сумма, измеряемая в денежных единицах, которую инвестор или вкладчик получает в виде прибыли, в виде вознаграждения.
В соответствии с принципом финансовой эквивалентности, при сравнении денежных величин, относящихся к разным моментам времени, следует пересчитать (привести) их к одному моменту времени. Такой пересчет осуществляется на основе формул роста или дисконтирования.
Рост — это преобразование текущей величины стоимости в оценку этой величины для будущего момента времени.
Дисконтирование — это преобразование будущей величины стоимости в оценку этой величины для настоящего момента времени.
Таким образом, рост и дисконтирование — взаимно обратные операции.
Рост по простой процентной ставке определяется формулой
Дисконтирование по простой учетной ставке определяется формулой