в чем измеряют объем жидкости
В чем измеряют объем жидкости
Знакомство ребенка с единицами измерения объема начинается с цифр. Сколько стаканов в литре? Что такое миллилитр? Объяснить эти и другие темы невозможно без использования числовых выражений, поэтому прежде чем приступать к теме, убедитесь, что ребенок умеет считать десятками и сотнями.
Задания, которые мы приводим в статье, взяли из тетради «Kumon. Меры объёма». Вы можете использовать их в качестве идей, чтобы на живых примерах объяснить эту тему. А можно распечатать задания и выполнить их.
Больше, меньше и равно
Сначала объясните ребенку, что такое «больше», «меньше» и «равно». Потренируйтесь определять, какой объем жидкости в ряду наибольший и какой наименьший.
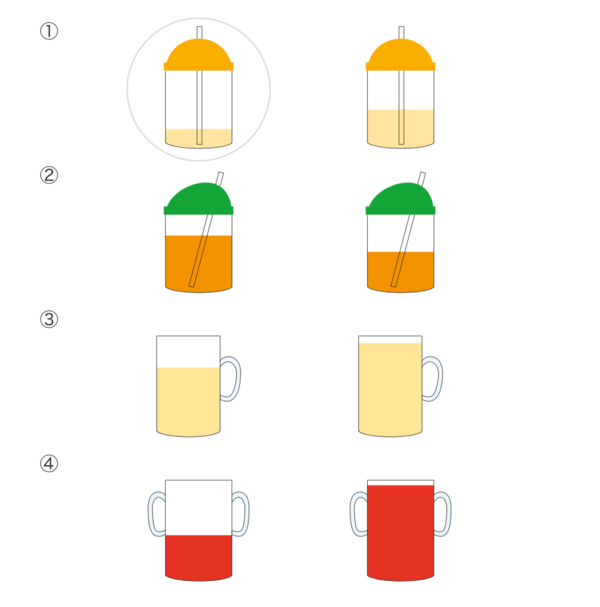
Пдф для скачивания
Здесь попросите определить, у какой из двух емкостей объем больше? Помогите ребенку увидеть емкость, которая вмещает больше стаканов жидкости.
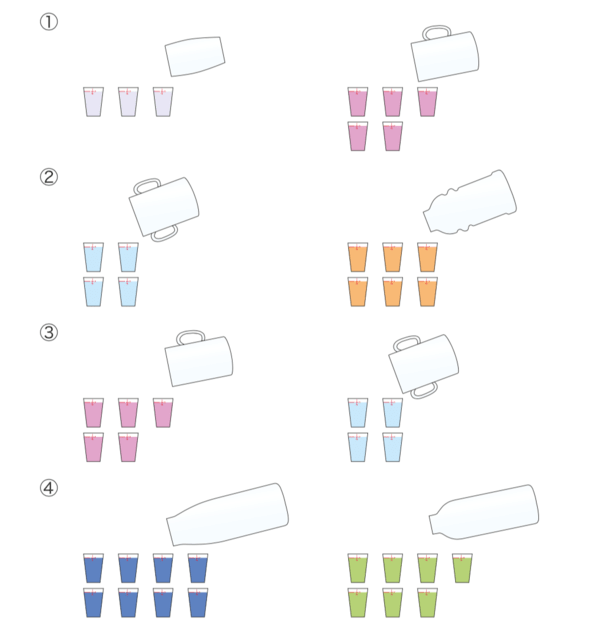
Пдф для скачивания
На этом этапе повторите устный счет от 1 до 1000 (десятками и сотнями) и написание чисел до 10, после чего можно учиться измерять объем жидкости в стаканах, литрах и миллилитрах.
Стаканы
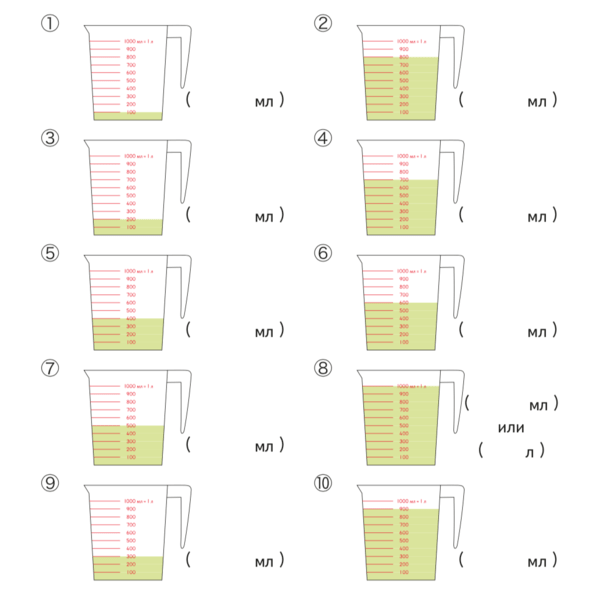
Покажите ребенку, что в каждой емкости помещается определенное количество стаканов жидкости. Попросите обвести в скобках число, обозначающее объем емкости, объясните, откуда взялись эти цифры (на рисунке показаны емкости, вмещающие то количество стаканов, которое изображено под ними).
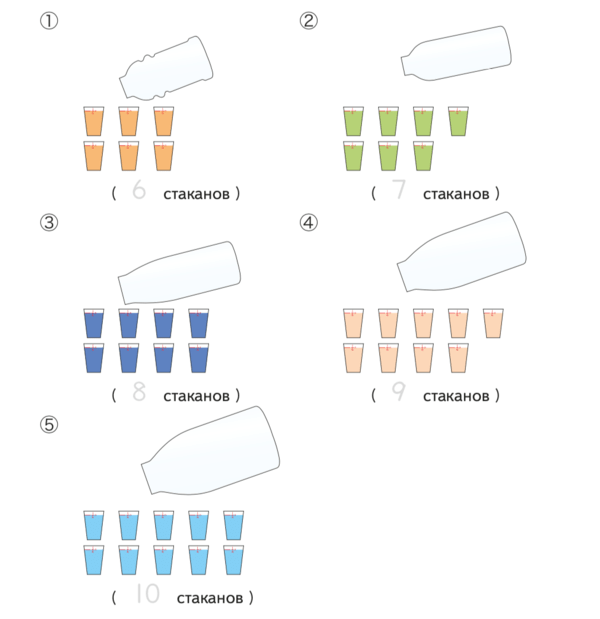
Пдф для скачивания
Расскажите ребенку, что объем жидкости — это место, которое жидкость занимает в емкости. Покажите на живых примерах: налейте воду в бутылки, кастрюли и другую посуду.

Скачайте сборник заданий на пространственное мышление→
Литры
Измерение объема — важная часть повседневной жизни. Умение пользоваться мерной емкостью с делениями пригодится и в школе, и дома.
Для закрепления материала желательно приобрести мерную емкость с четкой шкалой в миллилитрах и литрах. Поощряйте ребенка измерять жидкости и сыпучие продукты на кухне. Предложите ему самостоятельно налить нужное количество воды, молока или сока. Такие задания помогут развить и поддержать интерес к измерениям, повысят мотивацию к освоению этого полезного навыка, а также подарят опыт, закрепляющий теоретические знания.
После того, как вы рассказали ребенку о мере измерения в стаканах, переходите к понятию «литр». Покажите, что в мерном кувшине помещается 4 стакана жидкости, или 1 литр. Попросите ребенка обвести в скобках числа, обозначающие объем жидкости.
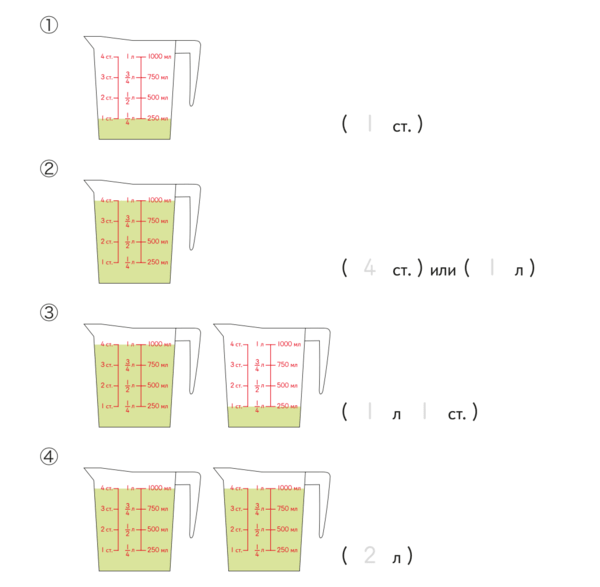
Пдф для скачивания
Миллилитры
Наверняка малыш заинтересуется, что означают эти деления на мерном стакане? Ребенок уже знает, что объем мерного кувшина — 1 литр. Теперь пришло время рассказать, что в одном литре — 1000 миллилитров. Выполните следующее задание: предложите ребенку написать в скобках числа, обозначающие объем жидкости.
Пдф для скачивания
Тетрадь «Kumon. Меры объёма» познакомит ребенка с понятиями «единицы измерения» и «объем». Выполнив все упражнения, ребенок поймет, как соотносятся друг с другом три меры объема, и сможет определить объем жидкости или сыпучих продуктов с помощью стакана и мерного кувшина.
Современные способы измерения объема жидкости
Одной из важнейших задач молочной промышленности всегда был учет объема продукта: поступившего на обработку, расходуемого в течение технологического процесса, полученного на выходе. Причем эти измерения требуются как для технологических задач, так и для экономического учета.
О современных способах произведения этих измерений и пойдет речь.Существует несколько подходов к измерению объема жидкости, находящейся в емкости. Все они, однако, имеют одну общую исходную величину, требуемую для расчета. Эта величина – высота столба жидкости.Известна формула, устанавливающая математическую связь между плотностью жидкости, высотой ее столба относительно точки измерения, ускорением свободного падения и давлением, оказываемым на дно и стенки сосуда:
где Р – давление, ρ – плотность жидкости, h – высота столба жидкости, g – ускорение свободного падения (9,8 м/c 2 ).
Итак, зная давление и плотность жидкости, нетрудно рассчитать высоту, до которой она доходит относительно точки измерения. Такой способ измерения называется гидростатическим.Для того, чтобы узнать давление жидкости используются соответствующие датчики. В пищевой промышленности, как правило, это датчики с мембраной, имеющие относительно большую плоскость контакта со средой, что позволяет легко отмывать их от остатков продукта.
Среди датчиков давления наиболее распространены датчики с выходным сигналом 4…20 мА, являющимся общемировым стандартом в системах автоматического управления. Например, интеллектуальный датчик давления 4000-SAN.Сам чувствительный элемент датчика обычно представляет собой тензорезистор – элемент, изменяющий свое сопротивление в зависимости от приложенного к нему усилия. Зависимость сопротивления этих элементов от давления известна. Далее изменение сопротивления электроника датчика приводит к сигналу 4…20 мА.Современные датчики давления часто делаются цифровыми – то есть роль преобразователя играет микроконтроллер, встроенный в датчик. Такие датчики легче настраивать, они обладают более высокой точностью и могут оснащаться дисплеями, модулями коммуникации и дополнительными функциональными возможностями.
Итак, после того, как получено значение высоты, можно переходить к расчету объема жидкости. Выделяются два основных практических подхода:
1. Первый способ измерения объема жидкости: вычисление высоты
Первый способ подразумевает возможность выражения зависимости высота – объем известной формулой. Он актуален для емкостей, имеющих несложную форму и построенных из таких стандартных геометрических фигур, как, например, полусфера, конус и цилиндр. Например, для широко распространенных емкостей в форме цилиндра с коническим дном (Рисунок 2), вычисление будет производиться следующим образом: до тех пор, пока жидкость не достигла края конуса зависимость ее объема от высоты такова:
Где V – объем, Нж – высота столба жидкости, K – конусность
как только высота жидкости достигает края конуса и начинает заполнять цилиндр достаточно взять заранее вычисленный полный объем конической части:
и прибавлять к нему объем жидкости, находящейся в цилиндрической части:
С учетом степени развития микроконтроллеров, подобный алгоритм возможно реализовать непосредственно в датчике. Не нужно никакое внешнее устройство – датчик сам вычислит объем жидкости, если ввести ее плотность и геометрию емкости.Этот способ, однако, имеет определенные недостатки и ограничения. Они будут рассмотрены далее.
2. Точность измерения давления, производимого датчиком
Отдельно нужно отметить требования к точности измерения давления, производимого датчиком. Нетрудно посчитать, что общепромышленный датчик давления, имеющий погрешность в 0,5 % для емкости высотой в 3 метра даст ошибку измерения в:
Значение не кажется столь большим. Однако, если емкость при этом имеет диаметр, скажем, в 2 метра, погрешность вычисления объема составит:
Достаточно большое значение, с учетом того, что в течение рабочего дня могут производиться десятки циклов наполнения/опустошения емкости. При этом данное значение не учитывает дополнительную погрешность, вызываемую перепадами температуры.Именно поэтому датчики для решения задач вычисления объема обычно имеют погрешность не более 0,1 %. При тех же условиях, такой датчик даст ошибку измерения всего в 9,42 литра, то есть в 5 раз меньшую.
3. Второй способ вычисления: аппроксимация
На практике часто встречаются емкости, имеющие искажения формы внутренней поверхности, к которым неприменим геометрический метод вычисления объема емкости.Например, для емкости, установленной под углом (Рисунок 2), наклон в 2…3 градуса, кажущийся незначительным, сильно нарушит точность измерений – в горизонтальной емкости поверхность жидкости вместо прямоугольника будет иметь гораздо более сложную форму, что значительно меняет зависимость объема от уровня.
Емкость может иметь утопленный в стенку люк. В этом случае нужно производить вычисления уже по трем разным формулам, вместо двух. К тому же, зависимость объема на участке с люком будет куда более сложной, чем для прямого цилиндра. Также, геометрический метод на практике неприменим к емкостям, в которых производится перемешивание продукта.
Массивное устройство внутри емкости значительно исказит результаты вычислений – датчик будет показывать объем, больший, чем реальный. Предусмотреть готовые алгоритмы для каждой подобной ситуации и внести их в датчик – задача практически невыполнимая. Тут на помощь приходит более трудоемкий, но и значительно более гибкий способ измерения. Если начать заливать в емкость, допустим, по 100 литров жидкости и при этом на каждом шаге отмечать высоту, соответствующую залитому объему, мы получим так называемую «тарировочную таблицу». Суть в следующем: нестандартная форма емкости моделируется с использованием некоторого количества прямых отрезков. Чем их больше, тем точнее будут производиться вычисления. Таким образом, можно высоте столба жидкости поставить в соответствие ее объем.
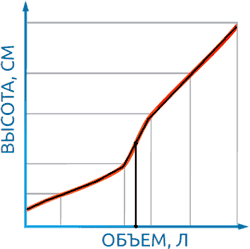
Если жидкость, например, находится посередине между двумя точками, то и объем вычисляется, как среднее значение объемов в этих точках (Рисунок 3). Очевидно, что от количества точек, используемых при тарировании, значительно зависит точность результата. Если для участка с линейной зависимостью объем/высота достаточно двух точек, до для нелинейных участков их требуется гораздо больше. Тарирование на нелинейном участке можно производить шагами, в два раза большими, чем допустимая погрешность на данном участке. Например, если в конусной части емкости необходимо получить точность не ниже 20 литров, шаги тарирования должны быть не более 40 литров. Тут следует помнить простое правило – чем меньше шаги и больше точек, тем выше итоговая точность работы. Недостаток метода в том, что датчик, перенесенный на другую емкость, снова потребует тарирования. Однако, единожды оттарированный на одной емкости датчик будет не только давать максимально высокую точность вычислений, но и позволит подсчитывать объем для жидкостей с различными плотностями – достаточно будет лишь ввести в него это значение.
Это значит, что можно произвести тарирование с использованием обычной воды, а затем, предварительно поменяв значение плотности жидкости в памяти датчика, заливать продукт, имеющий плотность, отличную от плотности воды. Таким образом, мы получаем гибкий и точный метод, позволяющий работать с емкостями любой формы и жидкостями любой плотности.
Инженер отдела проектирования ООО «КИП-Сервис»
Горбоносов М.А.
Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …
Как рассчитать объём ёмкости, воды или другой жидкости … несколько онлайн калькуляторов для расчёта объёма, формулы, а также конвертер единиц объёма.
Как рассчитать объём любой прямоугольной емкости, в том числе куба — онлайн калькулятор расчёта объема воды в аквариуме, баке …
Формула расчёта объёма прямоугольной ёмкости
V = X * Y * Z, где V — объём, а X, Y, и Z это длины сторон ёмкости (длина, ширина, высота).
Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать реальную заполненность ёмкости и привязывать величины непосредственно к самой жидкости.
Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →
Как рассчитать объём цилиндра — онлайн калькулятор расчёта объёма воды в трубе, бочке, круглом бассейне …
Для конвертации единиц объёма вы можете воспользоваться нашим ОНЛАЙН КОНВЕРТЕРОМ ЕДИНИЦ ОБЪЁМА →
Формулы расчёта объёма цилиндра:
Объём воды в цилиндре и других ёмкостях, имеющих цилиндрическую форму, рассчитывается таким образом.
Затем вычисляем объём — V = S * L
Где, L — длина (высота) цилиндра (трубы, бочки, бассейна).
Внимание! При расчёте объёма жидкости в ёмкости необходимо учитывать заполненность ёмкости и привязывать величины непосредственно к самой жидкости.
Единицы измерения объёма
Вначале кратко ознакомимся с единицами измерения объёма как таковыми.
Официальной единицей измерения объема в системе СИ является м 3 — метр кубической. Объём так же может быть выражен и в других единицах. Наиболее популярными из них являются — дм 3 — кубические дециметры, см 3 — кубические сантиметры, литры …
Отметим, что такая популярная единица измерения объёма жидкостей как литр не входит в Международную систему измерений (СИ). Тем не менее, поскольку литр является весьма популярной мерой жидкостей, он считается официальной внесистемной единицей.
Один литр — это объём куба стороны которого равны 10 см. Полезно также знать, что 1 литр воды вести приблизительно 1 кг при температуре + 4 °C
Соотношение единиц объёма
1 м3 = 1000 дм 3 = 1 000 000 см 3 = 1 000 000 000 мм 3 = 1000 литров
1 литр = 0,001 м 3 = 1 дм 3 = 1 000 см 3 = 1 000 000 мм 3
Конвертер единиц объёма
Конвертация кубических метров ( м 3 ) в кубические сантиметры ( см 3 ) и литры
Конвертация литров в метры кубические ( м 3 ) и кубические сантиметры ( см 3 )
Конвертация кубических сантиметров ( см 3 ) в кубические метры ( м 3 ) и литры
Заключение
Практически каждый человек рано или поздно сталкивается с необходимостью рассчитать объём того или другого объекта. Для удобства и экономии времени предлагаем Вам воспользоваться нашими онлайн калькуляторами.
Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …
1 комментарий к “Как рассчитать объём — калькулятор объёма куба, прямоугольной ёмкости, объёма цилиндра, объёма воды в трубе …”
Быстро и удобно если много объёмов
Оставьте комментарий Отменить ответ
Поделись с друзьями 🙂
Рубрики сайта
Публикации
Публикации
Поиск по сайту
Все материалы сайта защищены Законом «Об авторском праве и смежных правах». Сайт – vodamama.com является общедоступным и работает в рамках и в соответствии с действующим законодательством Украины.
Администрация ресурса может не разделять мнение автора. При подготовке материалов информация берётся из общедоступных источников и специальной проверки на достоверность не проходит.
Администрация сайта радикально негативно относится к нарушениям авторских или каких либо других имущественных прав. Поэтому, если Вы вдруг обнаружили, что на страницах нашего сайта нарушены, какие либо авторские или имущественные права, просим вас незамедлительно, воспользовавшись формой обратной связи, сообщить нам про это. После получения подтверждения нарушения мы незамедлительно устраним его.
Особенности определения вместимости сосуда
Что такое вместимость сосуда
Вместимость сосуда — это объем его внутренней полости, определяемый по его геометрическим параметрам. Единица измерения объема в СИ — кубический метр, но в случае жидкости чаще используют литр.
Особенности расчета объема жидкости в сосуде
Жидкость по своим свойствам занимает промежуточное место между двумя другими агрегатными состояниями вещества — твердым и газообразным. Жидкости присущи некоторые свойства и твердого тела, и газа. Силы взаимного притяжения молекул в жидкостях достаточно велики, чтобы удерживать молекулы вместе, так что, в отличие от газов, жидкости имеют постоянный собственный объем.
В то же время эти силы недостаточны, чтобы держать молекулы в жесткой упорядоченной структуре, и потому у жидкостей нет постоянной формы: они принимают форму сосуда, в котором находятся.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Жидкость в сосуде оказывает постоянное давление на его стенки, поэтому на производстве, где необходимо регулярно измерять текущий объем жидкости в сосуде, часто используют гидростатические датчики давления.
За счет маленького диаметра их мембран итоговая погрешность измерения близится к нулю. Поэтому, зная давление в конкретный момент времени, можно вычислять уровень жидкости, т. е. высоту гидростатического столба. В формулу для расчета входят только плотность жидкости и ее давление:
\(p\) здесь — давление в паскалях, \(\rho\) — плотность, \(g\) — ускорение свободного падения, константа.
Зная габариты сосуда, несложно рассчитать объем жидкости в нем. Это необходимо, например, в пивоварении и виноделии, где обычно используются цилиндрические емкости с конусным дном, близкие по параметрам к идеальным геометрическим телам.
При решении логических учебных задач на переливание жидкости из одного сосуда в другой может пригодиться понимание взаимосвязи объема жидкости и параметров сосуда. А для задач по физике часто требуется рассчитать объем, который занимает жидкость в сосуде, через ее массу. На практике это действительно один из самых удобных способов, не требующий ни специальных датчиков, ни сложных расчетов.
Найти объем керосина, зная массу одного и того же сосуда с ним, и без него. Масса пустого сосуда 440 грамм, полного — 600 грамм.
Плотность керосина можно узнать из справочной таблицы — 800 \(\frac<кг><м^<3>>.\)
Вычислим массу керосина в сосуде: 600 – 440 = 160.
Подставим известные данные в формулу:
Как определить вместимость сосудов разных форм
Вычисление объема параллелепипеда
Параллелепипед — это призма, объемная шестигранная фигура, в основании которой находится параллелограмм.
Прямоугольный параллелепипед — это призма, у которой все грани являются прямоугольниками. Прямоугольный параллелепипед, все грани которого являются квадратами, — это куб.
Чтобы вычислить объем прямоугольного параллелепипеда, достаточно найти произведение трех его измерений:
\(V = AB \times AD \times AA_ <1>= abc.\)
Объем куба равен кубу его стороны:
\(V = a^<3>.\)
Нахождение объема пирамиды
Пирамида — это многогранник, состоящий из основания — плоского многоугольника, вершины — точки, лежащей не в плоскости основания, и отрезков, которые соединяют вершину с углами основания. Высота пирамиды — это перпендикуляр, опущенный из вершины на плоскость основания.
\(V = \frac<1> <3>\times S_ <осн>\times h.\)
\(V = \frac<1> <3>\times h \times (S_ <1>+ S_ <2>+ \sqrt
Как найти объем цилиндра
Цилиндр — это тело, состоящее из двух кругов, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
\(R\) — радиус основания цилиндра, \(h\) — его высота, равная образующей оси.
\(V = S_ <осн>\times h = \pi \times R^ <2>\times h.\)
Как высчитать объем конуса
Конус — это тело, состоящее из круга, точки, лежащей не в плоскости этого круга, и отрезков, которые соединяют вершину с точками основания.
\(V = \frac<1> <3>\times S_ <осн>\times h = \frac<1> <3>\times \pi \times R^ <2>\times h.\)
\(V = \frac<\pi \times h> <3>\times (R_1^2 + R_2^2 + R_1 \times R_2).\)
Нахождение объема шара
Шар — это тело, состоящее из всех точек пространства, находящихся на расстоянии не больше заданного радиуса от центральной точки.
\(R\) — радиус полукруга, равный радиусу шара.
\(V = \frac<4\pi \times R^<3>><3>.\)
Измерение объема жидкости гидростатическим методом с корректировкой по плотности
Введение
Практически на любых предприятиях, производящих жидкие пищевые продукты (молоко, пиво, соки, квас и другие), для хранения или обработки сырья, жидких компонентов или готового продукта используются различные емкости. В процессе автоматизации производства и мониторинга зачастую требуется непрерывный контроль уровня жидкого продукта в этих емкостях. Существует несколько различных методов измерения уровня, однако в пищевой промышленности наибольшее распространение получил гидростатический метод измерения. Для его реализации используются специализированные датчики давления в санитарном исполнении.
При этом, по измеренному уровню продукта можно производить вычисление его объема, основываясь на геометрической форме емкости и плотности самого продукта. Например, на молочном заводе контроль объема требуется для учета всего поступающего на предприятие молока (в приемных молочных емкостях) или для сличения с показаниями объемных расходомеров в процессе транспортировки продукта между технологическими цехами. Однако измерение объема может стать нетривиальной задачей, если емкость имеет сложную форму, либо если плотность продукта изменяется.
В данной статье будет рассмотрен метод измерения объема продукта для емкостей любой формы, с автоматической корректировкой по плотности.
1 Расчет объема гидростатическим методом
Для реализации гидростатического метода измерения применяются датчики давления, которые устанавливаются в нижнюю часть емкости (см. рисунок 1) и измеряют гидростатическое давление столба жидкости.
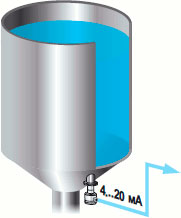
Далее, по измеренному давлению рассчитывается текущий уровень продукта:
И в дальнейшем, уже по рассчитанному уровню можно вычислить объем продукта в емкости. Например, для вертикальной цилиндрической емкости:
где:
S – площадь основания цилиндра, м 2 ;
h – уровень продукта, м.
Объединив (1) и (2), окончательно получим:
Исходя из полученной формулы (3), можно сделать вывод, что расчет объема зависит от трех параметров:
Рассмотрим каждый из параметров подробнее.
1.1 Погрешность измерения
Чем выше точность измерения датчика, тем больше рассчитываемый объем будет соответствовать реальному. Например, если используется датчик с классом точности 0,5 % и пределом измерения 0,4 бар, установленный в цилиндрической емкости с площадью дна 1 м 2 и высотой 4 метра, полностью заполненной водой, абсолютная погрешность измерения объема составит:
А в случае использования датчика с классом точности 0,1%, погрешность составит уже 4 литра, то есть в 5 раз меньше. Однако из-за особенностей производства жидких пищевых продуктов (молока, пива, вина и прочих) зачастую при измерении появляются дополнительные погрешности.
В пищевой промышленности, из-за непосредственного контакта со средой, применяются датчики давления с разделительной мембраной. Пространство под мембраной в датчике заполнено силиконовым пищевым маслом (утечка этого масла при повреждении мембраны не приводит к порче продукта). Сама мембрана имеет омываемую конструкцию, и таким образом продукт не имеет возможности застаиваться в датчике и со временем портиться. При этом емкости и технологическое оборудование, на которых установлены датчики, подвергаются высокотемпературной безразборной CIP-(Сleaning-in-place) или SIP-(Sterilization-in-place) мойке для устранения остатков продукта.
Помимо специализированной технологии изготовления мембраны, датчики обладают еще несколькими особенностями, очень важными для пищевой промышленности:
1.2 Геометрические особенности
Разумеется, рассмотренный выше пример с идеальной цилиндрической емкостью редко можно встретить на практике. Чаще на пищевых предприятиях применяют вертикальные емкости со сферическим или конусным дном (так называемые цилиндро-конические танки, или ЦКТ), а также горизонтальные цилиндрические емкости. Если емкость достаточно близка по форме к идеальному геометрическому телу, то ее объем можно рассчитать при помощи геометрических формул. Например, для распространенных в пивоварении и виноделии ЦКТ (см. рисунок 4) расчет объема представлен ниже.
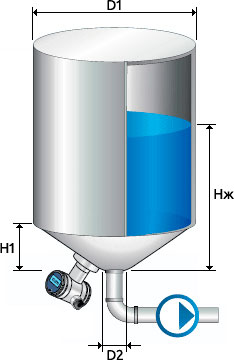
(если текущая высота жидкости h ≥ H1)
Рассмотренные выше расчеты можно производить программно на ПЛК, либо воспользоваться возможностями интеллектуальных датчиков давления. Например, в датчиках давления Klay Instruments серии 2000-SAN есть функция расчета объема по измеренному гидростатическому давлению для трех типов стандартных емкостей: вертикальных емкостей со сферическим дном, ЦКТ или горизонтальных емкостей круглой или овальной формы. После ввода требуемых геометрических размеров и текущей плотности жидкости датчик будет выдавать аналоговый сигнал 4…20 мА, пропорциональный объему в емкости (также возможна передача по HART-протоколу в цифровом виде).
Однако зачастую емкости имеют нестандартную форму или индивидуальные особенности. Например, если горизонтальная емкость имеет наклон (рисунок 5), либо в емкости есть перемешивающие устройства, технологические окна или люки (рисунок 6).
В этом случае необходима дополнительная процедура, называемая проливкой. Емкость последовательно заполняют фиксированными объемами воды (например, по 100 литров) известной плотности, и на каждом шаге наполнения фиксируют уровень по показаниям датчика давления. Тем самым, формируется функциональная зависимость между уровнем и пролитым объемом, индивидуальная для каждой емкости. Результаты проливки записываются в специальные проливочные или тарировочные таблицы — пример подобной таблицы представлен на рисунке 7.
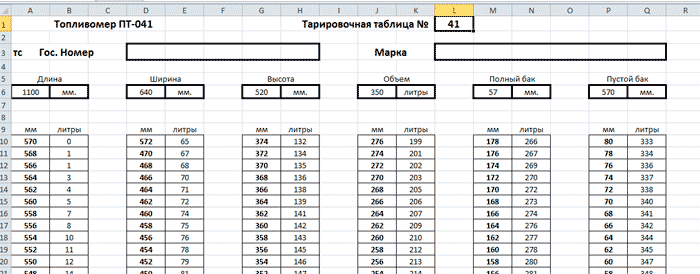
Саму процедуру проливки можно реализовать на программируемом логическом контроллере (путем кусочно-линейной аппроксимации), либо использовать функциональные возможности интеллектуального датчика серии 4000-SAN. Эти датчики позволяют произвести проливку и создать проливочную таблицу в реальном времени, используя встроенное ПО, либо ввести данные из уже имеющейся проливочной таблицы, в удобных для пользователя величинах.
Более подробно процесс пересчета объема по измеренному уровню описан в статье «Современные способы измерения объема жидкости».
1.3 Плотность продукта
Рассмотренные выше примеры расчета объема в емкостях различной формы актуальны при условии, что плотность продукта, находящегося в емкости, известна и строго постоянна. Однако есть ряд технологических процессов, в которых выполнить данное условие невозможно. В таких процессах могут возникать задачи измерения уровня или объема продукта с автоматической корректировкой по плотности, либо задачи измерения непосредственно самой плотности продукта. К таким процессам относятся:
Рассмотрим подробнее упомянутые выше методы измерения плотности.
2 Методы измерения плотности
Плотность традиционно определяют одним из двух способов:
Альтернативой рассмотренным традиционным способам может являться измерение плотности по показаниям двух гидростатических датчиков давления, установленных на определенном расстоянии друг от друга. Принцип измерения показан на рисунке 8. Реализация производится или на ПЛК, или на вторичном приборе.
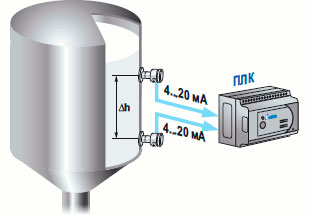
В случае использования ПЛК, аналоговые сигналы верхнего и нижнего датчиков давления подключаются к его входам, и программно производится вычисление плотности:
где:
Pн – показания давления нижнего датчика;
Pв –показания давления верхнего датчика;
Δh – строго известное расстояние между датчиками.
Важным условием работоспособности данного метода является выбор величины Δh. С одной стороны, чем больше это расстояние, тем точнее измеряется плотность и тем её измеренное значение будет более усредненным. С другой стороны, верхний датчик должен располагаться ниже верхнего уровня продукта, в противном случае измерение плотности будет невозможно. По этой причине описываемый метод расчета плотности применим, если уровень заполнения емкостей продуктом всегда выше определенной высоты, на которой и устанавливается верхний датчик.
Для получения наилучшей возможной точности измерения, рекомендуется применение датчиков серий 2000-SAN (относительная погрешность 0,1 %) или 4000-SAN (относительная погрешность 0,075 %). Причем датчики обладают возможностью настройки верхнего предела измерения (ВПИ). Поэтому рекомендуется произвести их перенастройку, поскольку погрешность датчиков этих серий нормируется для текущего настроенного диапазона измерений.
Пример №1 расчета погрешности
Максимальный уровень продукта в емкости составляет 4 метра, и в рабочем режиме не опускается ниже 3,5 метров.
В этом случае можно использовать модель 2000-SAN-2-W-H-G0 (диапазон измерения 0…0,12-1,2 бар) в качестве верхнего и нижнего датчиков. Для нижнего датчика настраивается ВПИ 0,4 бар. Верхний датчик следует замонтировать на высоте 3 метра (разница в 0,5 метра выбрана условно — датчику нужен некоторый уровень продукта над местом его монтажа, чтобы производились значимые измерения). Перенастройка датчика не потребуется, поскольку на заводе он настроен на минимальный ВПИ 0,12 бар.
Рассчитаем итоговую абсолютную погрешность измерения плотности для данного примера. Подставим в формулу (5) вместо величин Pн и Pв соответствующие им абсолютные погрешности, предварительно переведя единицы измерения давления в паскали. Абсолютные погрешности определим как произведение относительной погрешности и настроенного ВПИ. Сами абсолютные погрешности будем суммировать, поскольку они могут иметь разный знак. Получим:
Примечание: для упрощения не учитывалась погрешность преобразования аналогового сигнала или дополнительная погрешность измерения, вызванная отклонением температуры от нормальных условий.
Пример реализации подобной системы измерения плотности на базе датчиков 2000-SAN представлен на рисунке 9 — это машина формовки сыра. Установленные датчики контролируют среднюю плотность сырной массы на разной высоте колонны.

Однако не всегда есть возможность реализации программы на ПЛК. Поэтому расчет и индикацию плотности можно реализовать при помощи вторичного прибора ECV1-М производства ELHART (Россия). Это специализированный ПИД-регулятор, предназначенный для управления КЗР. Однако прибор обладает настолько широким функционалом, что может использоваться в качестве простого измерителя с возможностью дополнительных математических вычислений. А благодаря наличию интерфейса RS-485 (протокол ModBUS RTU), возможно как передавать вычисленные значения на верхний уровень АСУ ТП (в SCADA систему), так и производить конфигурацию прибора удаленно. Схема подключения обоих датчиков давления к прибору представлена на рисунке 10.
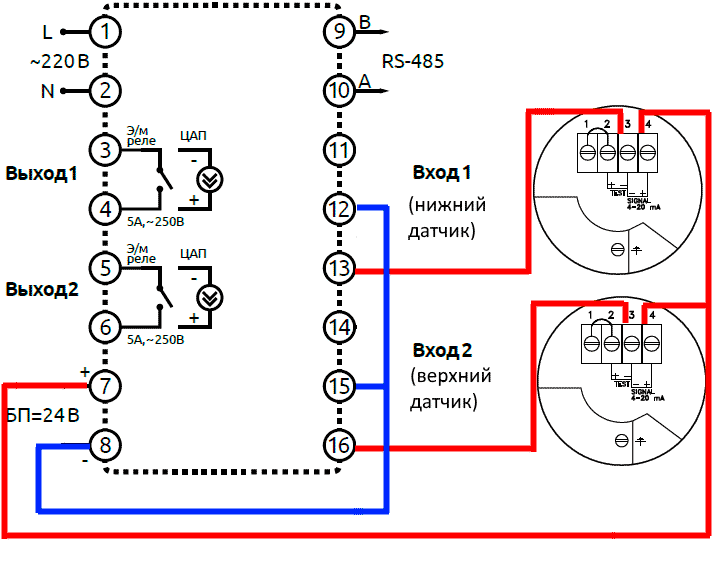
Параметры, которые необходимо настроить в приборе для вычисления и отображения, представлены в таблице 1.

