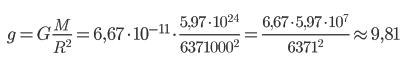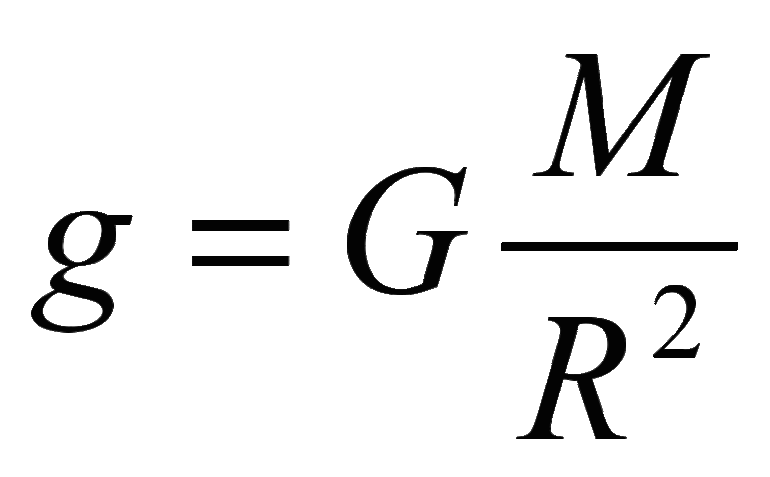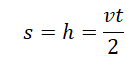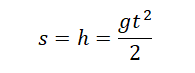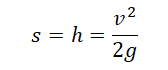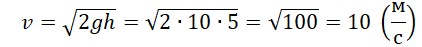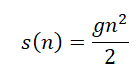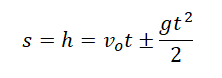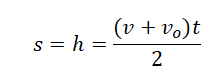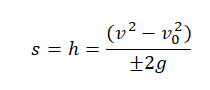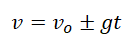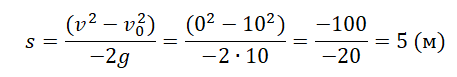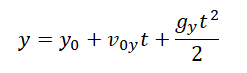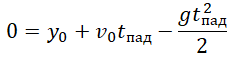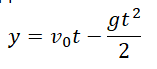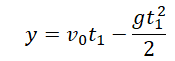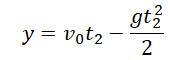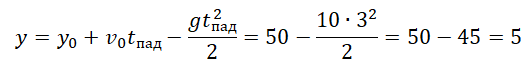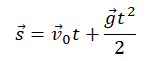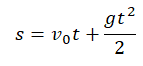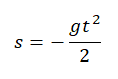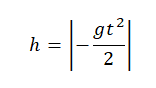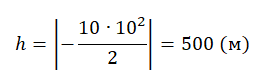в чем измеряется ускорение свободного падения в физике
Ускорение свободного падения
| Солнце | 273,1 | ||
| Меркурий | 3,68—3,74 | Венера | 8,88 |
| Земля | 9,81 | Луна | 1,62 |
| Церера | 0,27 | Марс | 3,86 |
| Юпитер | 23,95 | Сатурн | 10,44 |
| Уран | 8,86 | Нептун | 11,09 |
| Плутон | 0,61 |
Стандартное значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря.
где 

Содержание
Вычисление ускорения свободного падения
Ускорение свободного падения состоит из двух слагаемых: гравитационного ускорения и центробежного ускорения.
Значение гравитационного ускорения на поверхности планеты можно приблизительно подсчитать, представив планету однородным шаром массой M и вычислив гравитационное ускорение на расстоянии её радиуса R :


Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. Отличия обусловлены:
Исторически масса Земли была впервые определена Генри Кавендишем, исходя из известного ускорения свободного падения и радиуса Земли, и впервые измеренной им гравитационной постоянной.
Перегрузки
Ускорение свободного падения
Сила тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения
F — сила тяготения [Н]
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей. 🤓
Ускорение свободного падения
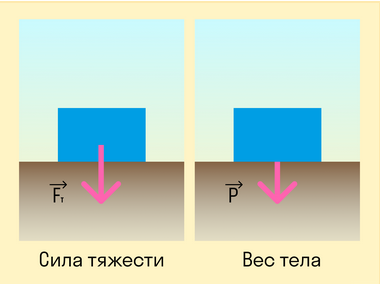
Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.
Сила тяжести — сила, с которой Земля притягивает все тела.
Сила тяжести
F = mg
F — сила тяжести [Н]
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.
Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
Приравниваем правые части:
Делим на массу левую и правую части:
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.
Формула ускорения свободного падения
g — ускорение свободного падения [м/с 2 ]
M — масса планеты [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.
Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.
Ускорение свободного падения на разных планетах
Выше мы уже вывели формулу ускорения свободного падения. Давайте попробуем рассчитать ускорение свободного падения на планете Земля.
Для этого нам понадобятся следующие величины:
Подставим значения в формулу:
И кому же верить?
Ниже представлена таблица ускорений свободного падения и других характеристик для планет Солнечной системы, карликовых планет и Солнца.
Небесное тело
Ускорение свободного падения, м/с 2
Диаметр, км
Расстояние до Солнца, миллионы км
Масса, кг
Соотношение с массой Земли
История открытия
Учёные Древней Греции разделяли любое движение на два типа: естественное и принудительное. Перемещение тела под воздействием гравитации считалось естественным, так как не имело видимой причины и происходило само собой.
Аристотель считал, что скорость падения напрямую зависит от массы. Это ошибочное утверждение родилось в результате примитивных наблюдений. Философ приводил в пример движение к земле яблок и листьев. Очевидно, что последние летели гораздо медленнее. Исследователи тех времён ещё очень мало понимали в физике. Такие понятия, как сопротивление воздуха и ускорение были неизвестны.
Утверждения Аристотеля считались неоспоримым постулатом вплоть до начала XVII века. Галилео Галлилей решительно отверг древнюю классификацию движения. В результате проведения нескольких опытов с движением тела по наклонной плоскости, учёный ввёл понятие ускорения.
Определение ускорения свободного падения в физике
Основное внимание Галлилей уделял изучению процесса свободного падения. Самым знаменитым стал эксперимент, проведённый на Пизанской башне.
С сооружения высотой 60-м были одновременно сброшены два предмета:
Результат был просто ошеломляющим. Оба тела достигли земли практически одновременно, а небольшая разница была объяснена силой сопротивления воздушной среды. Надо заметить, что наука тех лет существенно отличалась от сегодняшней. Считалось, что воздух не мешает падению, а, напротив, увеличивает его скорость.
Ещё одним заблуждением того времени было утверждение о том, что любое движение со временем прекращается, даже если на его пути нет преград. Галлилей опроверг и этот ошибочный закон физики, введя определение инерции.
В XVI веке ещё не существовало точных хронометров. Из-за этого ускорение падения тел с Пизанской башни было рассчитано довольно грубо. Для более точного измерения учёный изучал равноускоренное движение шарика по наклонной плоскости. А более или менее правильное значение ускорения сумел вычислить Гюйгенс в 1660 г.
Физическая сущность
Свободным падением может называться равноускоренное движение тела в результате действующей на него силы тяжести, происходящее в вакууме. Атмосфера Земли способна тормозить ускорение и замедлять падающие предметы. Однако, если величина сопротивления воздуха небольшая, ей можно пренебречь. К примеру, в опыте Галилея на башне в Пизе использовались шарообразные предметы, обладающие аэродинамичной формой. В результате этого коэффициент торможения удалось свести к минимуму.
Ускорение у поверхности Земли не зависит от массы предмета — это постоянная величина, обозначающаяся латинской буквой g и составляющая 9,80665 м/с.^2. Из-за воздействия центробежных сил на экваторе его значение немного меньше, а на полюсах, соответственно, больше.
Величина ускорения свободного падения зависит от нескольких факторов:
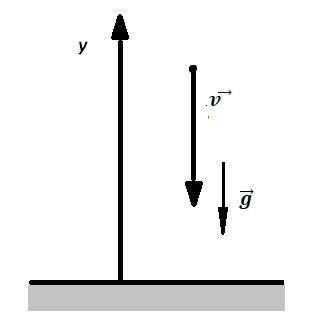
Вектор свободного падения всегда направлен вниз. Это можно наглядно увидеть, подбросив какой-либо предмет. Благодаря воздействию ускорения, его движение будет постепенно замедляться. Затем оно полностью остановится и направится в обратную сторону.
Формулы для расчёта
Галилей понимал, что исследование падения тел с Пизанской башни является несовершенным. Был поставлен новый эксперимент, в котором учёному удалось увеличить время движения и уменьшить сопротивление воздуха. Отполированные латунные шарики скатывались по желобам, расположенным под определённым углом наклона. В результате были выведен физический закон, согласно которому все падающие тела движутся с одинаковой, постоянно увеличивающейся скоростью.
Формула для нахождения: g=G (M/R ^ 2), где:
При помощи этой зависимости можно рассчитать значение g на поверхности любой планеты во вселенной.
Существуют задачи, для решения которых необходим более точный расчёт. В таком случае используется другая, расширенная формула: g=G (M/(R2+h)), где h — это высота над поверхностью планеты.
Стоит помнить, что для максимальной точности расчётов придётся учитывать большое количество факторов. Ускорение может измеряться при помощи специального прибора — гравиметра.
Ускорение на других планетах
Как видно из формулы, гравитационное ускорение напрямую зависит от массы и радиуса планеты. Из этого следует, что значение g на других планетах будет отличаться от земного.
Таблица показателя ускорения g для основных объектов Солнечной системы.
| Наименование | Ускорение, м/с. 2 |
| Солнце | 274,01 |
| Венера | 8,87 |
| Земля | 9,81 |
| Марс | 3,72 |
| Юпитер | 25,8 |
| Сатурн | 11,54 |
| Уран | 9,04 |
| Меркурий | 3,73 |
| Нептун | 11,33 |
| Луна | 1,69 |
Солнце является самым большим объектом в солнечной системе, его масса почти в 300 тыс. раз больше земной. Но как можно заметить из таблицы, ускорение на поверхности звезды превышает земное всего в 28 раз. Это объясняется огромным радиусом светила.
Во вселенной существуют очень компактные объекты с невероятной плотностью и чудовищным притяжением. Если взять среднюю нейтронную звезду с радиусом 13 км и массой 2,5*10 30 кг, то ускорение на её поверхности превысит земное в 100 млрд раз и составит довольно внушительное число — 9,87*10^11м/с. 2
Воздействие перегрузок на человека
Благодаря научно-техническому прогрессу и стремительному развитию технологий, современный человек имеет возможность пользоваться довольно быстрыми средствами передвижения. Чтобы попасть в любую точку планеты на самолёте, потребуется не более суток. Быстрая скорость передвижения неминуемо связана с таким понятием, как перегрузка.
Любая перегрузка являет собой отношение двух ускорений:
За единицу измерения принято брать гравитационное ускорение на Земле — 9,80665 м/с². Таким образом, нулевую перегрузку можно ощутить на себе лишь в невесомости.
Перегрузка является векторной величиной. Для людей и других живых организмов огромное значение имеет её направление. Это связано с тем, что организм приспособлен к постоянному воздействию гравитационного ускорения.
Характер положительной перегрузки заключается в том, что её вектор направлен вниз — от головы к ногам. Кровь оттекает от мозга и при показателе более 10 g человек может потерять сознание за считаные секунды. При отрицательном значении кровь, напротив, бьёт в голову. Это переносится гораздо хуже и может привести к кровоизлиянию и смерти.
Показатель перегрузки для различных ситуаций:
Военным и спортивным лётчикам приходится постоянно испытывать большие перегрузки. Для уменьшения вредного воздействия на организм существуют специальные защитные костюмы.
Переносить перегрузку лучше всего лёжа на спине. Именно в таком положении находятся космонавты при взлёте ракет.
Движение тела с ускорением свободного падения
теория по физике 🧲 кинематика
Свободное падение — это движение тела только под действием силы тяжести.
В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.
В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!
Ускорение свободного падения
Свободное падение
Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:
v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело
Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.
Подставляем данные в формулу и вычисляем:
Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.
Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.
Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.
Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:
Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:
Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.
Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:
Формула определения перемещения тела в n-ную секунду свободного падения:
s(n) — перемещение за секунду n.
Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.
Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх, описывается в два этапа
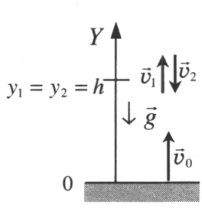
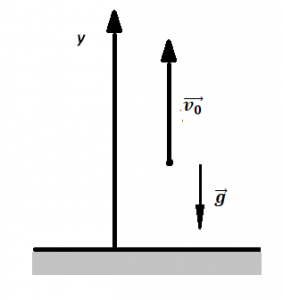
Два этапа движения тела, брошенного вертикально вверх Этап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v0 и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях ( v ↑↓ g ). Этап №2 — равноускоренное движение. Когда тело достигает верхней точки, и его скорость равна 0, начинается свободное падение с начальной скоростью до тех пор, пока тело не упадет или не будет поймано на некоторой высоте. На этом участке пути векторы скорости и ускорения свободного падения направлены в одну сторону ( v ↑↑ g ). Формулы для расчета параметров движения тела, брошенного вертикально вверх Перемещение тела, брошенного вертикально вверх, определяется по формуле:
Если известна скорость в момент времени t, для определения перемещения используется следующая формула:
Если время движения неизвестно, для определения перемещения используется следующая формула:
Формула определения скорости:
Какой знак выбрать — «+» или «–» — вам помогут правила:
Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h2 > h1). По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v2 > v01).
Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.
Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).
Уравнение координаты и скорости при свободном падении
Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:
Уравнение скорости при свободном падении:
Построение чертежа
Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.
Свободное падение на землю с некоторой высоты
Тело подбросили от земли и поймали на некоторой высоте
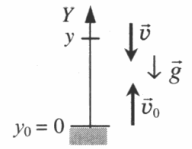
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Интервал времени между моментами прохождения высоты h:
Уравнение координаты для первого прохождения h:
Уравнение координаты для второго прохождения h:
Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.
Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Из условия задачи начальная скорость равна 0, а начальная координата — 50.
Через 3 с после падения тело окажется на высоте 5 м.
Алгоритм решения
Решение
Записываем исходные данные:
Перемещение (высота) свободно падающего тела, определяется по формуле:
В скалярном виде эта формула примет вид:
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
Вычисляем высоту, подставив известные данные:
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
Решение
Записываем исходные данные:
Записываем формулу для определения скорости тела в векторном виде:
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
Подставим известные данные и вычислим скорость:
pазбирался: Алиса Никитина | обсудить разбор | оценить