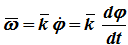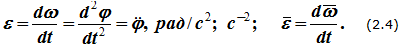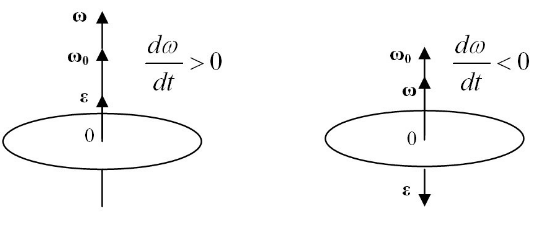в чем измеряется угловое ускорение в физике
iSopromat.ru
Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела:
Угловая скорость
Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.
Обозначение: ω (омега).
Формулы угловой скорости
Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:
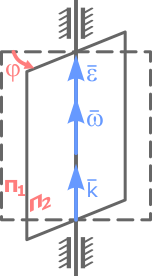
Быстрота изменения угла φ (перемещения из положения П1 в положение П2) – это и есть угловая скорость:
Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость
Приняв k как единичный орт положительного направления оси, получим:
Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.
Угловое ускорение
Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:
Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.
Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.
Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:
В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
В чем измеряется угловое ускорение? Пример задачи на вращение
Понятие об угловом ускорении
Очевидно, что прежде чем давать ответ на вопрос, в чем измеряется угловое ускорение в физике, следует познакомиться с самим понятием.
В механике линейного движения ускорение играет роль меры быстроты изменения скорости и вводится в физику через второй закон Ньютона. В случае вращательного движения существует аналогичная линейному ускорению величина, которая называется ускорением угловым. Формула для его определения записывается в виде:
То есть угловое ускорение α является первой производной угловой скорости ω по времени. Так, если скорость во время вращения не изменяется, то ускорение будет равно нулю. Если же скорость линейно зависит от времени, например, увеличивается постоянно, то ускорение α примет постоянное ненулевое положительное значение. Отрицательное значение α говорит о том, что система замедляет свое вращение.
Динамика вращения
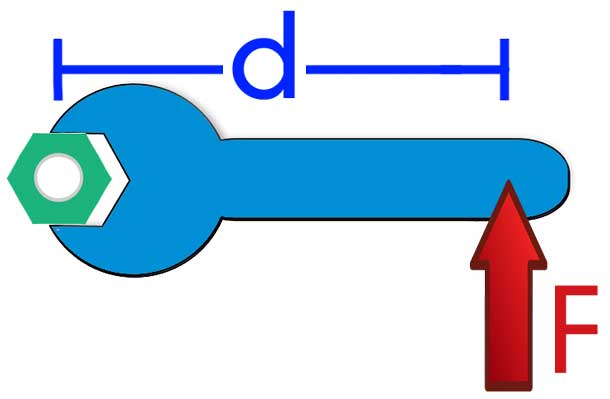
В физике всякое ускорение возникает только тогда, когда существует ненулевая внешняя сила, действующая на тело. В случае движения вращения эта сила заменяется на момент силы M, равный произведению плеча d на модуль силы F. Известное уравнение моментов динамики вращательного перемещения тел записывается в следующем виде:
α = M/I = [Н*м/(кг*м2)] = [Н/(кг*м)].
Мы получили единицу измерения α из уравнения моментов, тем не менее, ньютон не является базовой единицей СИ, поэтому его следует заменить. Для выполнения этой задачи воспользуемся вторым законом Ньютона, получаем:
α = 1 [Н/(кг*м)] = 1 кг*м/с2/(кг*м) = 1 [1/с2].
Мы получили ответ на вопрос, в каких единицах измеряется угловое ускорение. Оно измеряется в обратных квадратных секундах. Секунда, в отличие от ньютона, является одной из семи основных единиц СИ, поэтому полученная единица для α используется при математических расчетах.
Полученная единица измерения для углового ускорения является правильной, однако, по ней трудно понять физический смысл величины. В связи с этим поставленную задачу можно решить иным способом, используя при этом физическое определение ускорения, которое было записано в предыдущем пункте.
Угловые скорость и ускорение
Вернемся к определению углового ускорения. В кинематике вращения угловая скорость определяет угол поворота за единицу времени. В качестве единиц измерения угла можно использовать либо градусы, либо радианы. Последние чаще применяются. Таким образом, угловая скорость измеряется в радианах в секунду или сокращенно рад/с.
Рассматриваемая единица для α аналогична той, которая была получена в предыдущем пункте статьи, где значение радиан было опущено, поскольку оно подразумевается в соответствии с физическим смыслом углового ускорения.
Угловое и центростремительное ускорения
Ускорение центростремительное обеспечивает лишь искривление траектории тела во время вращения, угловое же ускорение приводит к изменению линейной и угловой скоростей. Так, в случае равномерного движения по окружности угловое ускорение равно нулю, центростремительное же ускорение имеет некоторую постоянную положительную величину.
Угловое ускорение α связано с линейным касательным ускорением a следующей формулой:
Решение задачи
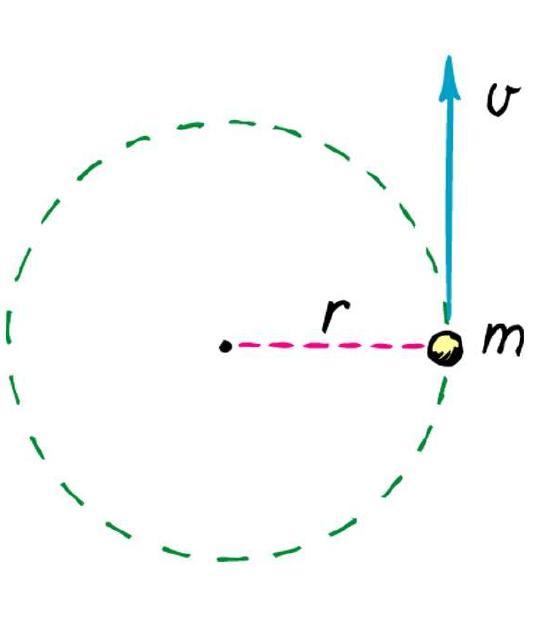
Решим следующую задачу из физики. На материальную точку действует касательная к окружности сила 15 Н. Зная, что эта точка имеет массу 3 кг и вращается вокруг оси с радиусом 2 метра, необходимо определить ее угловое ускорение.
Решается эта задача с использованием уравнения моментов. Момент силы в данном случае равен:
Момент инерции точки рассчитывается по следующей формуле:
I = m*r2 = 3*22 = 12 кг*м2.
Тогда значение ускорения будет равно:
α = M/I = 30/12 = 2,5 рад/с2.
Таким образом, за каждую секунду движения материальной точки скорость ее вращения будет увеличиваться на 2,5 радиана в секунду.
Угловое ускорение
Система понятий кинематики включает в себя также такую величину как угловое ускорение тела. Дадим ей определение, рассмотрим основные аспекты с использованием примеров.
Основные понятия
Угловое ускорение – величина, характеризующая изменение скорости с течением времени.
Числовое значение ускорения в заданный момент времени есть первая производная от угловой скорости или вторая производная от угла поворота по времени.
Ускоренное вращение тела – это вращение, при котором угловая скорость (ее модуль) возрастает с течением времени.
Замедленное вращение тела – это вращение, при котором угловая скорость (ее модуль) убывает с течением времени.
В общем, довольно просто заметить, что, если ω и ε имеют одинаковые знаки, наблюдается ускоренное вращение, а, когда противоположные знаки – замедленное.
Закон равнопеременного вращения
Проинтегрируем вторично и получим формулу, выражающую закон равнопеременного вращения:
Вращение является равноускоренным, когда ω и ε имеют одинаковые знаки.
Вращение является равнозамедленным, когда ω и ε противоположны по знаку.
Практические примеры
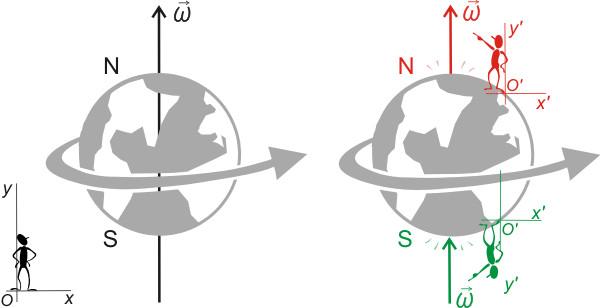
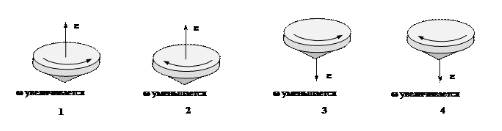
На рисунке 2 заданы различные типы вращения гироскопа (волчка). С учетом соответствующих подписей необходимо указать, какой рисунок верно демонстрирует направление углового ускорения.
Запишем выражения для угловой скорости и углового ускорения заданной точки:
Полное ускорение запишем как:
Угловое ускорение
Угловое ускорение – это псевдовекторная физическая величина, которая равна первой производной от псевдовектора угловой скорости по времени:
.
Угловое ускорение характеризует силу изменения модуля и направления угловой скорости при движении твердого тела.
Ускорение точки твердого тела при свободном движении.
К понятию углового ускорения можно прийти, изучая определение ускорения точки твердого тела, находящегося в свободном движении. Определение скорости точки тела В (по формуле Эйлера) в свободном движении:
.
где 
— скорость точки тела А, которая была принята как полюс; 
— псевдовектор угловой скорости тела; 
— вектор, который был выпущен из полюса в точку – его скорость определяем. Продифференцировав это выражение по времени данное выражение, получаем:
.
где 
— является ускорением полюса А; 
— псевдовектором углового ускорения.
Составляющая ускорения точки В, которая определяется через угловое ускорение называется вращательным ускорением точки В около полюса А.
.
Последнее слагаемое в полученной формуле, которое зависит от угловой скорости, называется осестремительным ускорением точки В вокруг полюса А.
.
Угловое ускорение при вращении тела вокруг неподвижной оси.
Когда происходит вращение тела около неподвижной оси, которая проходит через недвижимые точки тела О1 и О2, производные орта оси вращения = 0:
.
Отсюда вектор углового ускорения вычисляется тривиально через вторую производную угла поворота
или 
.
где 
— это алгебраическая величина углового ускорения.
Здесь псевдовектор углового ускорения (и угловая скорость) идет по оси вращения тела. В случае наличия одинакового знака у первой и второй производной угла поворота:
,
значит, вектор углового ускорения и вектор угловой скорости имеют одинаковое направление и тело имеет ускоренное вращение. Иначе, при 
, векторы угловой скорости и углового ускорения имеют противоположные направления, а, значит, тело вращается замедленно.
В теормехе обычно вводится понятие угловой скорости и углового ускорения, когда рассматривается вращение тела вокруг не двигающейся оси. При чем, для решения задачи используют зависимость от времени угла поворота тела
Отсюда закон движения точки тела можно выразить натурально, как длина дуги окружности, которую прошла точка, совершая поворот тела от определенного исходного положения φ0 = φ (t0)
где R является расстоянием от точки до оси вращения.
Продифференцировав вышеуказанное выражение по времени, найдем алгебраическую скорость точки:
.
где 
является алгебраической величиной скорости угловой.
Через геометрическую сумму тангенциального и нормального ускорения можно выразить ускорение точки тела при вращении:
.
При этом тангенциальное ускорение выходит в виде производной от алгебраической скорости точки:
.
где 
является алгебраической величиной углового ускорения. А при помощи ниже приведенной формулы определим нормальное ускорение точки тела:
.
Угловое ускорение Как рассчитать и примеры
угловое ускорение это изменение, которое влияет на угловую скорость, принимая во внимание единицу времени. Он представлен греческой буквой альфа, α. Угловое ускорение является векторной величиной; следовательно, он состоит из модуля, направления и смысла.
Единицей измерения углового ускорения в Международной системе является радиан в секунду в квадрате. Таким образом, угловое ускорение позволяет определить, как угловая скорость изменяется во времени. Угловое ускорение, связанное с равномерно ускоренными круговыми движениями, часто изучается.
Таким образом, при равномерно ускоренном круговом движении значение углового ускорения является постоянным. Наоборот, при равномерном круговом движении значение углового ускорения равно нулю. Угловое ускорение эквивалентно в круговом движении тангенциальному или линейному ускорению при прямолинейном движении.
На самом деле его значение прямо пропорционально значению тангенциального ускорения. Таким образом, чем больше угловое ускорение колес велосипеда, тем больше испытываемое ускорение.
Следовательно, угловое ускорение присутствует как в колесах велосипеда, так и в колесах любого другого транспортного средства, при условии изменения скорости вращения колеса..
Аналогично, угловое ускорение также присутствует в колесе, поскольку оно испытывает равномерно ускоренное круговое движение, когда оно начинает свое движение. Конечно, угловое ускорение также можно найти в карусели.
Как рассчитать угловое ускорение?
В общем, мгновенное угловое ускорение определяется из следующего выражения:
Среднее угловое ускорение также можно рассчитать из следующего выражения:
В частном случае плоского движения бывает, что как угловая скорость, так и угловое ускорение являются векторами с направлением, перпендикулярным плоскости движения..
С другой стороны, модуль углового ускорения можно рассчитать по линейному ускорению с помощью следующего выражения:
Круговое движение равномерно ускорено
Как уже упоминалось выше, угловое ускорение присутствует в равномерно ускоренном круговом движении. По этой причине интересно знать уравнения, которые управляют этим движением:
θ = θ0 + ω0 ∙ t + 0,5 ∙ α ∙ t 2
Крутящий момент и угловое ускорение
В случае линейного движения, согласно второму закону Ньютона, для того, чтобы тело приобрело определенное ускорение, требуется сила. Эта сила является результатом умножения массы тела и ускорения, которое испытало то же самое.
Однако в случае кругового движения сила, необходимая для придания углового ускорения, называется крутящим моментом. Короче говоря, крутящий момент можно понимать как угловую силу. Обозначается греческой буквой τ (произносится «тау»).
Аналогичным образом, необходимо учитывать, что во вращательном движении момент инерции I тела выполняет роль массы в линейном движении. Таким образом, крутящий момент кругового движения рассчитывается по следующему выражению:
примеров
Первый пример
Также определите значение мгновенного углового ускорения, когда прошло 10 секунд с начала движения..
решение
Выражение угловой скорости можно получить из выражения положения:
ω (t) = d Θ / dt = 12 т 2 я (рад / с)
Как только мгновенная угловая скорость была вычислена, мгновенное угловое ускорение может быть вычислено как функция времени.
α (t) = dω / dt = 24 t i (рад / с) 2 )
Чтобы вычислить значение мгновенного углового ускорения по истечении 10 секунд, необходимо только заменить значение времени в предыдущем результате..
α (10) = = 240 i (рад / с) 2 )
Второй пример
Определите среднее угловое ускорение тела, которое испытывает круговое движение, зная, что его начальная угловая скорость была 40 рад / с и что через 20 секунд она достигла угловой скорости 120 рад / с..
решение
Из следующего выражения вы можете рассчитать среднее угловое ускорение:
Третий пример
Каково будет угловое ускорение колеса, которое начинает двигаться с равномерно ускоренным круговым движением, пока через 10 секунд оно не достигнет угловой скорости в 3 оборота в минуту? Каким будет тангенциальное ускорение кругового движения в этот период времени? Радиус колеса составляет 20 метров.
решение
Во-первых, необходимо преобразовать угловую скорость из оборотов в минуту в радианы в секунду. Для этого выполняется следующее преобразование:
ωF = 3 об / мин = 3 ∙ (2 ∙ Π) / 60 = Π / 10 рад / с
Как только это преобразование выполнено, можно рассчитать угловое ускорение, учитывая, что:
α = Π / 100 рад / с 2
А тангенциальное ускорение возникает в результате действия следующего выражения: