в чем измеряется тангенциальное ускорение
Нормальное и тангенциальное ускорение
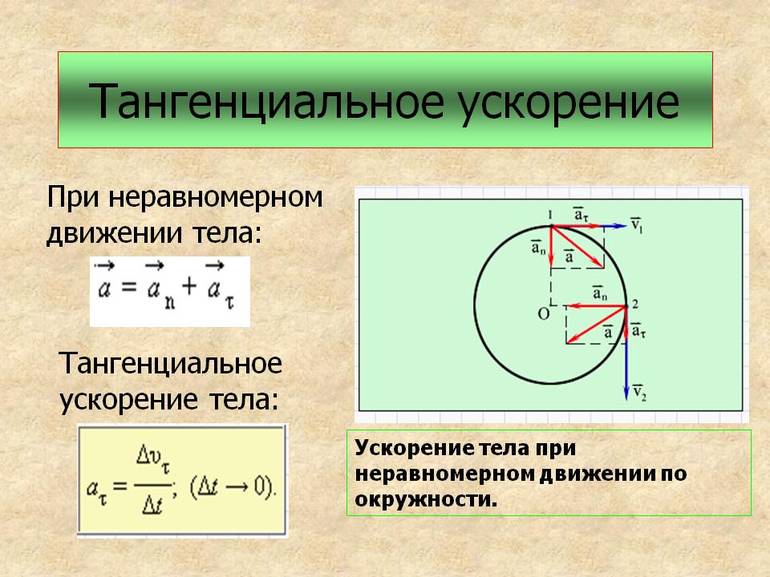
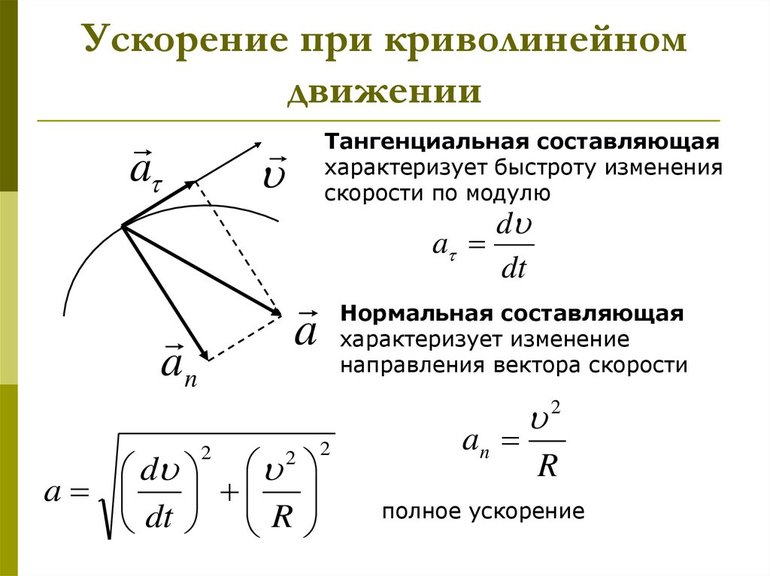
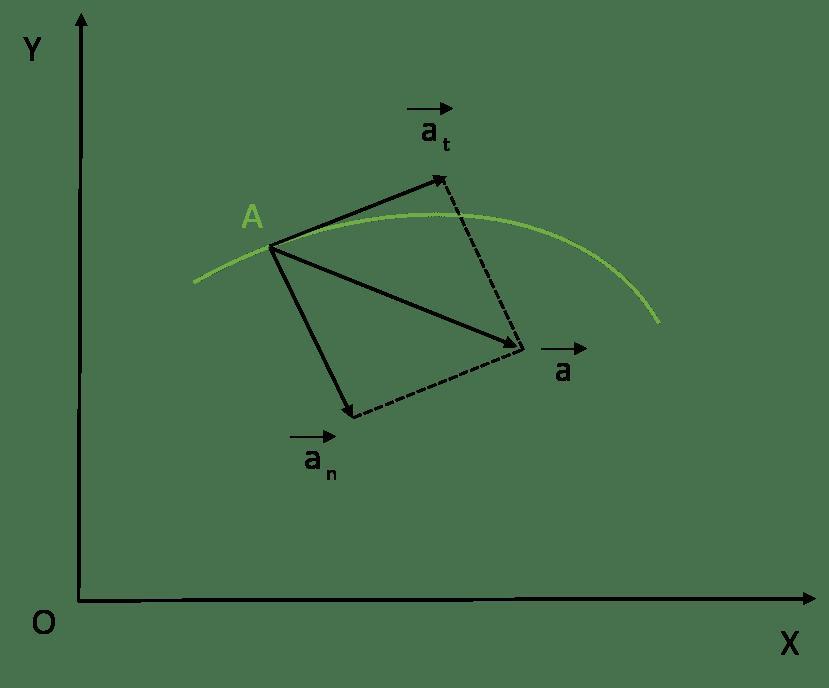
Тангенциальным (касательным) ускорением называют ту составляющую вектора ускорения, которая направлена по касательной к траектории в данной точке траектории движения. Тангенциальное ускорение описывает степень изменения скорости по модулю при совершении криволинейного движения.
Если тело движется по криволинейной траектории, то его скорость направлена по касательной к этой траектории.
Так как направление скорости все время меняется, значит, в таком случае криволинейное движение всегда происходит с ускорением, также, если модуль скорости не меняется.
В большинстве случаев ускорение направлено под некоторым углом к скорости. Составляющую ускорения, которая направлена вдоль скорости, называют тангенциальным ускорением 
Нормальное ускорение 
Здесь R – это радиус кривизны траектории в заданной точке.
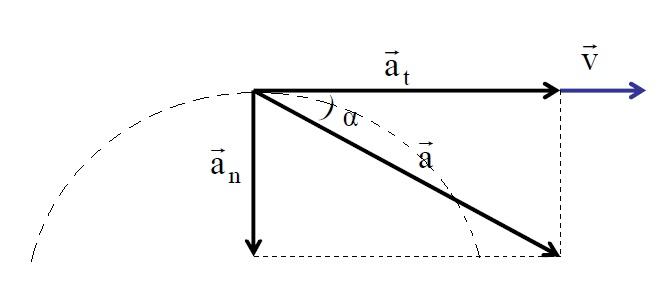
Тангенциальное и нормальное ускорение всегда имеют перпендикулярное направление, откуда получаем модуль полного ускорения:

Что такое ускорение?
Ускорение — физическая векторная величина, которая характеризует насколько быстро тело (материальная точка) изменяет скорость своего движения. Ускорение является важной кинематической характеристикой материальной точки.
Самый простой вид движения — равномерное движение по прямой линии, когда скорость тела постоянна и тело за любые равные промежутки времени проходит одинаковый путь.
Но большинство движений неравномерны. На одних участках скорость тела больше, на других меньше. Машина начиная движение двигается все быстрее. а останавливаясь замедляется.
Если скорость тела при неравномерном движении за любые равные промежутки времени изменяется одинаково, то движение называют равноускоренным.
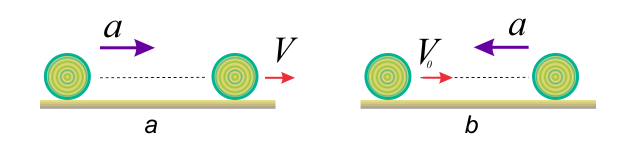
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
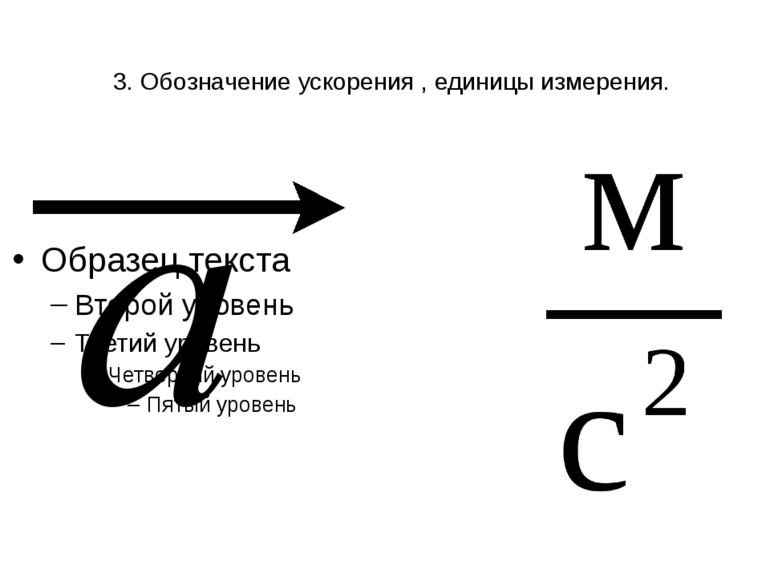
Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с, т. е. метр в секунду за секунду. Эту единицу обозначают 1 м/с2 и называют «метр на секунду в квадрате».
Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.
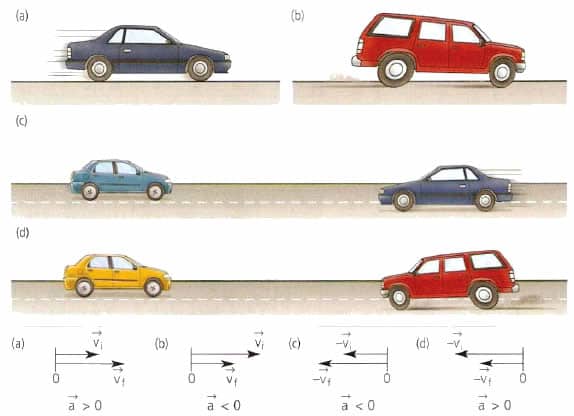
Если скорость тела при равноускоренном прямолинейном движении возрастает, то ускорение направлено в ту же сторону, что и скорость (рис. а); если же скорость тела при данном движении уменьшается, то ускорение направлено в противоположную сторону (рис. б).
Среднее и мгновенное ускорение
Среднее ускорение материальной точки на некотором промежутке времени — это отношение изменения его скорости, что произошло за это время, к продолжительности этого промежутка:
Тангенциальное и нормальное ускорение
\( = \dfrac
где \( \theta \) — угол между вектором скорости и осью абсцисс; \( \hat n \) — орт перпендикуляра к скорости.
где \( \vec a_ <\tau>= \dfrac
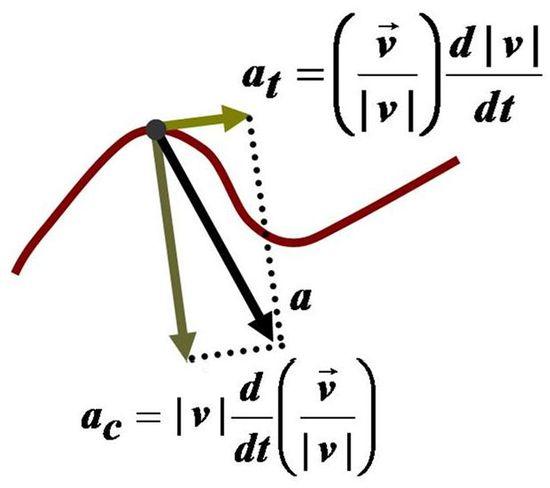
Учитывая, что вектор скорости направлен по касательной к траектории движения, то \( \hat n \) — это орт нормали к траектории движения, который направлен к центру кривизны траектории. Таким образом, нормальное ускорение направлено к центру кривизны траектории, в то время как тангенциальное — по касательной к ней. Тангенциальное ускорение характеризует скорость изменения величины скорости, в то время как нормальное характеризует скорость изменения ее направления.
\( a_
Измерение ускорения
Ускорение измеряется в метрах (разделенных) на секунду во второй степени (м/с 2 ). Величина ускорения определяет, насколько изменится скорость тела за единицу времени, если оно будет постоянно двигаться с таким ускорением. Например, тело, движущееся с ускорением 1 м/с 2 за каждую секунду изменяет свою скорость на 1 м/с.
Общие сведения
Первая лекция для студентов, изучающих кинематику, начинается с рассмотрения тангенциального ускорения, характеризуемого произвольным движением. По сути, рассматривается неравномерное прямолинейное движение общего вида. Кинематика входит в механику и изучает перемещение объектов без учёта сил, вызвавших их движение. Под перемещением понимают изменение положения в пространстве по отношению к другому физическому телу, которое и считается точкой отсчёта. Если изменение положения связать с координатами и временем, то образуется система отсчёта. С её помощью можно определить положение объекта в любой момент.
В кинематике любые процессы принято рассматривать, приняв тело за материальную точку. То есть его размерами и формой пренебрегают. При изменении за какой-то промежуток времени точка проходит путь, описывающийся линией — траекторией. Она является скалярной величиной, а само перемещение — векторной. Движение материальной точки может происходить с разной скоростью и ускорением. Быстроту движения разделяют на среднюю и мгновенную. Вторая определяется как предел, к которому стремится скорость на бесконечно малом временном интервале: v = Δs / Δt (Δt → 0).
Перемещение может происходить с ускорением. Это физическая величина, определяющая изменение быстроты перемещения. Иными словами, показывает изменение положения за единицу времени. Измеряется она в метрах на секунду в квадрате. В кинематике существует три вида ускорения:
Но также используется понятие «вектор среднего ускорения тела». Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.
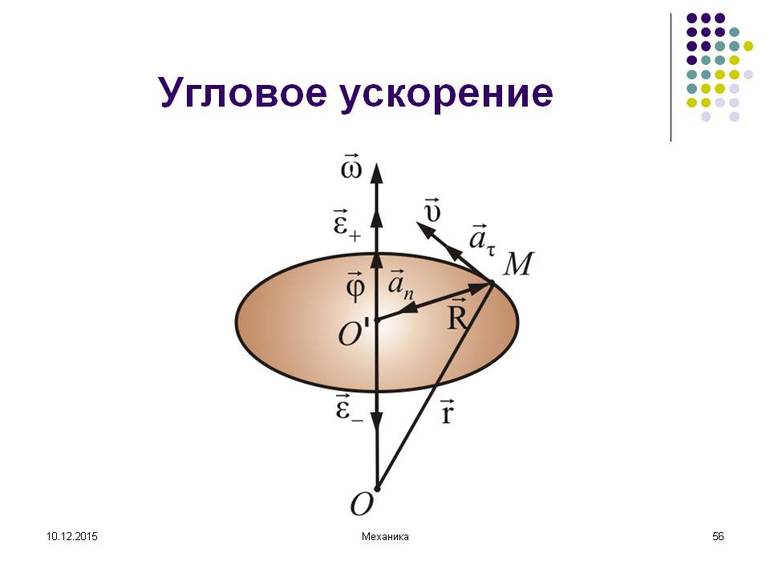
Угловое ускорение
Если имеется какая-то точка, находящаяся на вращающемся теле, то скорость её направлена по касательной. Когда движение равномерное, то линейная скорость связана с угловой равенством: v = w * r. А вот ускорение тела будет направлено по радиусу к центру окружности, причём модуль вычисляется как a = v / r либо если это точка на вращающемся теле: a = w2 * r.
В момент, когда тело поворачивается за небольшой промежуток времени на угол дельта фи, угловую скорость можно связать с условием поворота через формулу: w = Δ φ / Δ t. Если тело вращается равномерно, то промежуток времени может быть любым. В ином случае эта величина будет равна мгновенной угловой скорости.
Можно представить, что материальная точка движется неравномерно, то есть изменяется угловая скорость тела. Линейная скорость не будет представлять собой постоянную величину, в отличие от равномерного перемещения. Угол поворота равняется: w = v / r. Так как скорость не может быть константой, то отсюда следует, что и угловая скорость не будет постоянной величиной. Её изменение обозначают Δw. Она равняется разности конечной угловой скорости и начальной: Δw = wк — wн.
Изменение угловой скорости можно разделить на промежуток времени, за который оно поменяло значение: (wк — wн) / Δt. По сути, получается ускорение. Обозначается характеристика буквой эпсилон E и называется угловым ускорением. Измеряется характеристика в радианах на секунду в квадрате. Её смысл заключается в описании физической величины через отношение изменения угловой скорости тела за небольшой промежуток времени к длительности этого промежутка.
Пусть есть дуга окружности с центром. В начальный момент времени у тела есть скорость, направленная по касательной к траектории v0. Через некоторое время точка переместится по окружности на небольшое расстояние. Так как движение неравномерное, модуль скорости изменится v ≠ v0. Для того чтобы найти ускорение тела, нужно воспользоваться следующей формулой: a = Δv / Δt, при этом Δv = v — v0.
Чтобы найти эту разность, нужно воспользоваться правилом треугольника. Для этого следует перенести вектор V0 к V и соединить их линией. Радиус от центра к материальной точке можно обозначить R. Дельта V можно представить, как сумму взаимно перпендикулярных векторов. Один из них будет направленных тангенциально к радиусу, в физике обозначают его Δ Vτ, а другой радиально Δ Vr. В итоге: ΔV = Δ Vτ + Δ Vr.
Вывод формулы
Для доказательства формулы необходимо рассмотреть плоскую систему координат, в которой материальная точка изменяет своё положение по криволинейной траектории. В начальный момент её скорость будет равняться V0. Через некоторое время она изменится и станет V. На графике в плоском измерении это можно представить в виде синусоиды. В определённый момент времени скорость превышает начальную: V > V0. На схеме вектор нулевой скорости направлен из точки t0 вверх по касательной, а вектор V с нижней точки синусоиды параллельно оси ординаты.
Исходя из графика, можно сделать два вывода:
Для того чтобы построить вектор изменения Δv, нужно из конечной точки отрезка V0 провести линию к рассматриваемой точки, характеризующейся во времени скоростью V. Вершины полученного треугольника можно обозначить буквами ABD. Из верхнего угла B на сторону AD можно опустить медиану. Точка пересечения со стороной пусть будет C. Получается, что вектор Δv можно разложить на две составляющие — отрезки BC и СD. Причём медиана равняется Δvn, а изменение по оси ординаты Δvt.
Для разложения необходимо использовать вектор АС, длина которого совпадает с Vo по модулю: |AC| = |AB| = V0. Так как Δvn — результирующий вектор, то его можно вычислить через сумму: Δv = Δvn + Δvt. Причём первый член в равенстве характеризует изменение быстроты за промежуток времени по направлению, а второй — по модулю. Исходя из того, что t не равняется нулю, на него можно разделить левую и правую часть равенства: Δv / Δt = Δvn / Δt + Δvt / Δt. Если дельта-времени стремится к нулю, то формулу можно переписать в виде: lim Δv / Δt = lim Δvn / Δt + lim Δvt / Δt.
Учитывая связь между ускорениями и то, что полное значение состоит из суммы изменения быстроты движения по модулю и направлению, можно утверждать о верности формулы: a = at + an. Так как направление векторов ускорения и скорости всегда совпадают, то последний можно представить, как параметр, состоящий из двух взаимно перпендикулярных компонент:
Решение простых примеров
В школьном курсе на уроках физики учащимся для закрепления материала предлагается решить определённый тип задач, используя определение тангенциального ускорения. Это типовые примеры, объясняющие суть характеристики и её применение в реальной практике. Вот некоторые из них.
Но не всегда решаемые задания можно решить, обойдясь одной формулой. При этом значения тех или иных величин могут быть довольно сложными для проведения вычислений. В таких случаях есть резон использовать так называемые онлайн-калькуляторы. Это специализированные сайты, выполняющие подсчёт в автоматическом режиме. Из таких сервисов можно выделить: сalc, widgety, webmath. Указанные интернет-решители работают на русском языке, так что вопросов, как с их помощью выполнять расчёты, возникнуть не должно.
Сложная задача
Пусть имеется физическое тело, которое движется, замедляясь по окружности радиусом R так, что в каждый момент времени её тангенциальное и нормальное убыстрение равны друг другу по модулю. Необходимо найти зависимость скорости и полного ускорения от времени и пройденного пути. В начальный момент скорость равняется V0.
Согласно условию, тангенциальное ускорение будет отрицательным, так как точка движется, замедляясь. Для понимания задачи можно изобразить схему движения. Для этого необходимо нарисовать окружность и указать на ней вектор начальной скорости, тангенциального и нормального ускорения. Изобразить вектор полного ускорения как сумму векторов.
Подставив пределы, можно получить равенство: (1 / V) — (1 / V0) = t / R. Из полученной формулы следует выразить скорость: V = (V0 * R) / (R + V0 * t). Поделив числитель и знаменатель на радиус, ответ примет вид: V (t) = V0 / (1 + (V0 * t / R)).
Понятия о скорости, тангенциальном и нормальном ускорениях. Формулы
Чтобы уметь решать различные задачи на движение тел по физике, необходимо знать определения физических величин, а также формулы, с помощью которых они связаны. В этой статье будут рассмотрены вопросы, что такое тангенциальная скорость, что такое полное ускорение и какие компоненты его составляют.
Понятие о скорости
Двумя основными величинами кинематики перемещения тел в пространстве являются скорость и ускорение. Скорость описывает быстроту перемещения, поэтому математическая форма записи для нее имеет следующий вид:

Как известно, всякое тело движется по воображаемой линии, которая называется траекторией. Вектор скорости всегда направлен по касательной к этой траектории, в какой бы точке не находилось движущееся тело.
Существует несколько названий величины v¯, если рассматривать ее совместно с траекторией. Так, поскольку направлена она по касательной, то ее называют тангенциальной скоростью. Также о ней могут говорить, как о линейной физической величине в противоположность угловой скорости.
Вычисляется скорость в метрах в секунду в СИ, однако на практике часто пользуются километрами в час.
Понятие об ускорении
Измеряется ускорение в м/с2. Например, известное всем ускорение свободного падения является тангенциальным при вертикальном подъеме или падении объекта. Его величина вблизи поверхности нашей планеты составляет 9,81 м/с2, то есть за каждую секунду падения скорость тела увеличивается на 9,81 м/с.
Причиной появления ускорения является не скорость, а сила. Если сила F оказывает действие на тело массой m, то она неминуемо создаст ускорение a, которое можно вычислить так:
Эта формула является прямым следствием из второго закона Ньютона.
Полное, нормальное и тангенциальное ускорения
Скорость и ускорение как физические величины были рассмотрены в предыдущих пунктах. Теперь мы подробнее изучим, какие компоненты составляют полное ускорение a¯.
Предположим, что тело движется со скоростью v¯ по криволинейной траектории. Тогда будет справедливо равенство:
Вектор u¯ имеет единичную длину и направлен вдоль касательной линии к траектории. Воспользовавшись таким представлением скорости v¯, получим равенство для полного ускорения:
a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.
Полученное в правом равенстве первое слагаемое называется тангенциальным ускорением. Скорость связана с ним тем фактом, что она количественно определяет изменение абсолютного значения величины v¯, не принимая во внимание ее направление.
Если обозначить как at и an тангенциальную и нормальную составляющие полного ускорения a, тогда модуль последнего можно вычислить по формуле:
Связь тангенциального ускорения и скорости
Соответствующую связь описывают кинематические выражения. Например, в случае движения по прямой с постоянным ускорением, которое является тангенциальным (нормальная составляющая равна нулю), справедливы выражения:
В случае движения по окружности с постоянным ускорением эти формулы так же справедливы.
Таким образом, какой бы ни была траектория перемещения тела, тангенциальное ускорение через тангенциальную скорость рассчитывается, как производная по времени от ее модуля, то есть:
Например, если скорость изменяется по закону v = 3*t3 + 4*t, тогда at будет равно:
Скорость и нормальное ускорение
Запишем в явном виде формулу для нормальной компоненты an, имеем:
an¯ = v*du¯/dt = v*du¯/dl*dl/dt = v2/r*re¯
Нормальное ускорение появляется всегда, когда изменяется вектор скорости, однако оно равно нулю, если этот вектор сохраняет направление. Говорить о величине an¯ имеет смысл только тогда, когда кривизна траектории является конечной величиной.
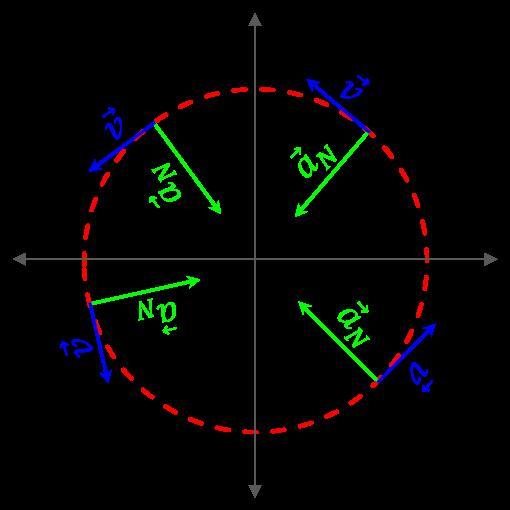
Выше мы отмечали, что при движении по прямой линии нормальное ускорение отсутствует. Однако в природе существует тип траектории, при движении по которой an имеет конечную величину, а at = 0 при |v¯| = const. Этой траекторией является окружность. Например, вращение с постоянной частотой металлического вала, карусели или планеты вокруг собственной оси происходит с постоянным нормальным ускорением an и нулевым тангенциальным ускорением at.
Понятие об ускорении. Ускорение тангенциальное, нормальное и полное. Формулы
Каждый, кто знаком с техникой и физикой, знает о понятии ускорения. Тем не менее мало кто знает о том, что эта физическая величина имеет две составляющие: ускорение тангенциальное и ускорение нормальное. Рассмотрим подробнее каждое из них в статье.
Что такое ускорение?
В физике ускорением называют величину, которая описывает быстроту изменения скорости. Причем под этим изменением понимают не только абсолютное значение скорости, но и ее направление. Математически это определение записывают так:
Заметим, что речь идет о производной изменения вектора скорости, а не только ее модуля.
В отличие от скорости, ускорение может принимать как положительные, так и отрицательные значения. Если скорость направлена всегда вдоль касательной к траектории перемещения тел, то ускорение направлено в сторону действующей на тело силы, что следует из второго закона Ньютона:
Ускорение измеряется в метрах в секунду квадратную. Так, 1 м/с2 означает, что скорость на 1 м/с увеличивается за каждую секунду перемещения.
Прямолинейная и криволинейная траектории движения и ускорение
Окружающие нас объекты могут двигаться либо по прямой линии, либо по кривой траектории, например, по окружности.
В случае движения по прямой скорость тела изменяет только свой модуль, но сохраняет направление. Это означает, что полное ускорение может быть вычислено так:
Отметим, что мы опустили значки вектора над скоростью и ускорением. Поскольку полное ускорение направлено по касательной к прямолинейной траектории, то оно называется тангенциальным или касательным. Эта составляющая ускорения описывает исключительно изменение абсолютной величины скорости.
Теперь предположим, что тело совершает движение по криволинейной траектории. В этом случае его скорость можно представить в виде:
a¯ = dv¯/dt = d(v*u¯)/dt = dv/dt*u¯ + v*du¯/dt.
Это и есть исходная формула нормального, тангенциального и полного ускорения. Как видно, равенство в правой части состоит из двух слагаемых. Второе из них отлично от нуля только при криволинейном перемещении.
Формулы тангенциального ускорения и нормального ускорения
Формула для касательной компоненты полного ускорения уже была приведена выше, запишем ее еще раз:
Формула показывает, что тангенциальное ускорение не зависит от того, куда направлен вектор скорости, и меняется ли он во времени. Оно определяется исключительно изменением абсолютного значения v.
Несложно показать геометрически, что эта формула может быть упрощена до такого вида:
Нормальное ускорение направлено к центру кривизны траектории, поэтому его называют центростремительным. Причиной его возникновения являются центральные силы в системе, которые изменяют траекторию. Например, это сила гравитации при вращении планет вокруг звезд или сила натяжения веревки при вращении камня, привязанного к ней.
Полное ускорение при вращении по окружности
Разобравшись с понятиями и формулами тангенциального ускорения и нормального ускорения, можно теперь переходить к вычислению полного ускорения. Решим эту задачу на примере вращения тела по окружности вокруг некоторой оси.
Рассмотренные две компоненты ускорения направлены под углом 90o друг к другу (по касательной и к центру кривизны). Этот факт, а также свойство суммы векторов можно использовать, чтобы рассчитать ускорение полное. Получаем:
Из формулы полного, нормального и тангенциального ускорений (ускорения an и at) следует два важных вывода:
Во время движения по окружности центростремительная сила, сообщающая телу ускорение an, удерживает его на круговой орбите, препятствуя тем самым фиктивной центробежной силе.