в чем измеряется сосредоточенная нагрузка
Виды нагрузок или в чем сила, сопромат?
В данном случае имеются в виду физические силы, а всякие там силы духа, мысли, третьего глаза и тому подобные не рассматриваются. Во всяком случае до тех пор, пока телепаты и экстрасенсы не начнут вместо подъемных механизмов работать на стойках народного хозяйства, силой мысли перемещая панели и плиты перекрытия, а не ложки и стаканы в различных телешоу.
Нагрузками, наиболее часто рассматриваемыми при расчете строительных конструкций, являются массы тел (причем далеко не всегда только физическая масса, а иногда еще и инерционная, но об этом чуть позже) и разница давлений. Но это далеко не все, что можно сказать о нагрузках.
В теоретической механике и сопромате принято различать нагрузки, действующие на рассчитываемые конструкции или элементы конструкций, по различным признакам. Одним из таких признаков является время действия нагрузки. По времени действия нагрузки делятся на постоянные и временные:
Постоянные нагрузки
Нагрузки, действующие на конструкцию в течение всего времени эксплуатации конструкции, будь то одна секунда или одно тысячелетие.
Временные нагрузки
Это все остальные нагрузки, действующие на конструкцию.
В свою очередь временные нагрузки принято разделять на длительные и кратковременные:
Длительные нагрузки
Кратковременные нагрузки
Для более точного определения нагрузки дополнительно разделяются на статические и динамические.
Статические нагрузки
Условно говоря, это силы, приложенные с минимальным ускорением или с ускорением, стремящимся к нулю.
Таким образом действие инерционной силы при столь малых ускорениях стремится к нулю и расчет ведется только на действие силы от физической массы. Или так: При воздействии статических нагрузок происходит относительно медленное нарастание деформаций, и потому инерционными массами отдельных элементов конструкции, перемещающихся в процессе деформации, можно пренебречь, так как ускорения таких перемещений являются незначительными. В результате этого равновесие между внешними и внутренними силами в любой момент действия статической нагрузки остается как бы неизменным.
К статическим относятся постоянные и длительные нагрузки, иногда кратковременные нагрузки.
Динамические нагрузки
Это нагрузки, изменяющиеся не только во времени, но и в пространстве.
Для динамических нагрузок характерна относительно большая скорость приложения, что требует при расчетах учитывать инерционную массу как объекта, создающего нагрузку, так и элемента, подвергающегося воздействию нагрузки. Другими словами, следует учитывать характер движения объекта создающего нагрузку, а также то, что инерционные массы элементов конструкции, подвергающиеся воздействию динамической нагрузки, перемещаются с ускорением и влияют на напряженно-деформированное состояние элементов. Чтобы учесть это влияние, в уравнения статического равновесия к внешним и внутренним силам добавляются силы инерции на основании принципа Даламбера. Добавление инерционных сил позволяет рассматривать любую движущуюся систему как находящуюся в состоянии статического равновесия в любой момент времени. Таким образом динамические нагрузки вызывают в материале исследуемого элемента конструкции динамические напряжения и поведение материала при этом оказывается отличным от поведения при статических напряжениях.
В свою очередь динамические нагрузки в зависимости от характера движения бывают также нескольких видов. Для строительных конструкций наиболее важными являются подвижные и ударные нагрузки:
Подвижные нагрузки
Это нагрузки возникающие в результате перемещения некоего объекта по поверхности исследуемой конструкции (вдоль рассматриваемой оси элемента).
Ударные нагрузки
Это нагрузки, возникающие в момент соприкосновения перемещающегося объекта с поверхностью исследуемой конструкции (вдоль или поперек рассматриваемой оси элемента).
Однако и это еще не все варианты классификации нагрузок. По площади приложения нагрузки делятся на сосредоточенные и распределенные.
Сосредоточенные нагрузки
Это силы, площадь приложения которых пренебрежимо мала по сравнению с площадью рассчитываемой конструкции.
Распределенные нагрузки
Это все остальные нагрузки, т.е. силы, распределяющиеся по длине и ширине элемента.
Разнообразие распределенных нагрузок поистине не поддается описанию. Распределенные нагрузки могут равномерно и неравномерно распределенными, равномерно и неравномерно изменяющимися по длине или ширине, при этом характер изменения нагрузки может описываться уравнением параболы, синусоиды, окружности, овала и любым другим уравнением.
А самое примечательное во всем этом то, что один и тот же человек в зависимости от ситуации может рассматриваться и как сосредоточенная нагрузка и как распределенная, и как статическая и как динамическая и только постоянной нагрузкой человек быть не может.
В целом все это выглядит не совсем понятно, однако ничего страшного в этом нет, как говорится, лучше один раз рассчитать конструкцию, чем 100 раз прочитать, как это делается. Примеров расчета на сайте хватает. А кроме того, понимание основ сопромата позволяет в большинстве случаев определять нагрузки так, чтобы максимально упростить расчет.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Сопротивление материалов. Шпаргалка для студентов
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
Приведённый ознакомительный фрагмент книги Сопротивление материалов. Шпаргалка для студентов предоставлен нашим книжным партнёром — компанией ЛитРес.
2. Классификация сил
Любой элемент конструкции можно рассматривать как самостоятельный, если воздействие остальных элементов считать силами внешнего воздействия. К внешним силам относят как силы, действующие со стороны других элементов, так и реакции связей (опор). Действующую на тело систему сил принято называть нагрузкой.
Внешние силы принято делить на объемные, т. е. распределенные по всему объему, и поверхностные, действующие только на поверхность рассматриваемого элемента. Поверхностные силы в свою очередь подразделяются на сосредоточенные и распределенные по поверхности элемента или по длине элемента. Если сила передается на деталь по площадке, размеры которой пренебрежимо малы в сравнении с площадью всего элемента конструкции, силу считают сосредоточенной. Это упрощение служит для облегчения расчетов. Распределенные по поверхности нагрузки характеризуются давлением, т. е. отношением силы, действующей на элемент нормально к нему, к площади данного элемента. Распределенная по длине нагрузка характеризуется интенсивностью, выражаемой единицей силы, отнесенной к единице длины.
Сосредоточенные силы измеряются в ньютонах (H), распределенные по поверхности (давление) — в паскалях, распределенные по длине (интенсивность нагрузки q) — в ньютонах на метр (Н/м).
Также нагрузки подразделяются по характеру изменения во времени.
Статические нагрузки характеризуются постоянством во времени.
Динамические нагрузки, абсолютное значение, направление и место приложения которых изменяются во времени. Такие нагрузки могут быть кратковременными или действующими продолжительно и изменяющимися по какому-либо закону.
Укажем самые распространенные типы связи.
Односвязная опора (шарнирно-подвижная) изображена на Рис. 1.1. Реакция такой опоры всегда перпендикулярна опорной поверхности.
Двухсвязная опора (шарнирно-неподвижная) схематически изображена на Рис. 1.2.
Реакция этой опоры проходит через центр шарнира, ее направление зависит от действующих сил. Вместо отыскания числового значения и направления этой реакции удобнее найти две ее составляющие.
В трехсвязной опоре (жесткой заделке), изображенной на Рис. 1.3 возникают реактивная пара сил (момент) и реактивная сила, последнюю удобнее представлять в виде двух ее составляющих.
Нагрузка в теоретической механике
Вы будете перенаправлены на Автор24
При расчетах в теоретической механике встречается такое понятие как нагрузка. Она может распределяться вдоль заданной поверхности, согласно определенному закону.
Понятие нагрузки в теоретической механике
В качестве одного из важнейших понятий в теоретической механике выступает нагрузка. Она является мерой механического взаимодействия тел и становится определяющей для интенсивности и направления такого взаимодействия.
Механическим называется такое взаимодействие двух тел, которое способно изменять их кинематическое состояние.
Для классификации нагрузок в теоретической механике важное значение имеют такие понятия, как сила и момент (пара сил).
Силу определяют три элемента: числовое значение (модуль), точка приложения и направление. Изображением силы выступает вектор. Прямая, по которой такая сила направляется, выступает в качестве линии действия силы. Единицей силы в СИ считается ньютон (н).
Готовые работы на аналогичную тему
Классификация нагрузок в теоретической механике
Нагрузки в теоретической механике классифицируются в зависимости от их значения. Они бывают статистическими, повторно-переменными, динамическими, распределенными по поверхности или сосредоточенными.
Статистические нагрузки или остаются неизменными со временем или изменяются достаточно медленно. При действии таких нагрузок производится расчет прочности. Повторно-переменный вид нагрузок характеризуется многократным изменением только значения или еще дополнительно знака. Действие такого типа нагрузок провоцирует усталость металла.
Динамические нагрузки характеризуются изменением своего значения за короткий промежуток времени, способствуют большим ускорениям, вызывают силы инерции и провоцируют внезапное разрушение конструкции. В зависимости от способа приложения, нагрузки бывают: сосредоточенные или распределенные по поверхности.
Передача нагрузки между деталями на самом деле осуществляется не в одной точке, а на определенной площадке, нагрузка таким образом будет распределенной. В то же время, если размеры площадки контакта окажутся незначительными в сравнении с размерами самой детали, сила будет считаться сосредоточенной.
Замена распределенного типа нагрузки на сосредоточенную не требуется, если производятся расчеты реальных деформируемых тел. В сопротивлении материалов аксиомы теоретической механики применяются ограниченно. Не допускается:
Все вышеперечисленные действия способствуют изменению распределения внутренних сил в конструкции.
Распределенная и сосредоточенная нагрузка
В реальности зачастую встречаются силы, которые приложены не к самой точке, а к поверхности или объему тела. Речь может идти о силе тяжести, например, или давлении ветра. Нагрузка будет в таком случае восприниматься не бесконечно малой площадкой, а значительной площадью или объемом тела. Эти силы называются распределенными. Распределенная нагрузка с постоянной интенсивностью по всей длине участка считается равномерно распределенной
Примером такой нагрузки может быть снег, выпавший на крышу дома. Своей силой тяжести снежный покров оказывает давление на всю поверхность крыши, в равной степени нагружая при этом каждую единицу ее площади, а не отдельно взятую точку.
Нагрузки (виды нагрузок, единицы измерения нагрузок).
Нагрузки (виды нагрузок, единицы измерения нагрузок).
Нагрузки – это внешние силы, действующие на конструкцию.
Сила – это мера механического воздействия одного тела на другое.
Единица измерения – ньютон (Н).
Также приблизительно можно принять:
1тонна =1000кг =10000Н =10кН
а) По длительности воздействия – постоянные, временные, переменные.
Б) По характеру приложения – распределённые и сосредоточенные.
В) По характеру воздействия – статические и динамические.
Статическая нагрузка медленно возрастает от нуля до своего конечного значения и остаётся постоянной в процессе работы детали или конструкции.
Динамическая нагрузка мгновенно возрастает от нуля до своего конечного значения и её значение непостоянно в процессе работы детали или конструкции.
Расчетные схемы.
При расчётах в сопромате для упрощения графической части реальные конструкции заменяются расчётными схемами, т.е. вместо чертежа детали или конструкции изображают упрощённую схему и по ней проводят расчёты.
Внутренние силовые факторы, метод сечений.
При действии на тело внешних сил внутри тела возникают силы сопротивления, которые называются внутренними силовыми факторами.
При различных видах деформаций возникают определённые внутренние силовые факторы. Всего при различных видах деформаций возникает шесть внутренних силовых факторов, которые характеризуют все виды деформаций, существующие в природе.
1. N – продольная сила, возникает при деформации растяжение и сжатие.
Это поперечные силы, возникают при деформации сдвиг.
Это изгибающие моменты, возникают при деформации изгиб.
6. МZ =Т – крутящий момент, возникает при деформации кручение.
Чтобы вычислить внутренние силовые факторы, применяется метод сечений, который заключается в том, что тело мысленно рассекается на две части, одна часть отбрасывается, а другая рассматривается и вместо отброшенной части прикладываются внутренние силовые факторы. Значения внутренних силовых факторов вычисляются из уравнений равновесия.
Напряжение.
Нормальное напряжение.
Касательное напряжение.
Напряжение – это мера интенсивности действия внутренних сил.
При действии на конструкцию внешней нагрузки в материале конструкции возникает механическое напряжение, которое характеризует интенсивность внутренних сил. Если нагрузку постепенно увеличивать, то значение напряжения тоже будет увеличиваться, и когда оно достигнет какого – то критического значения, произойдёт разрушение материала.
Полное напряжение р разложим на две оси, одна из них перпендикулярна к поперечному сечению конструкции, другая параллельна.
σ – нормальное напряжение, возникает при деформации растяжение или сжатие, всегда направлено перпендикулярно к поперечному сечению конструкции.
τ – касательное напряжение, возникает при деформации сдвиг, всегда направлено параллельно к поперечному сечению конструкции.
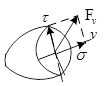
Рассмотрим нормальное напряжение. Оно вычисляется по следующей формуле:
где S – площадь поперечного сечения конструкции
Единица измерения напряжения (Н/м2 ) =Па
Так как величина Па очень маленькая, то на практике применяют величину
[σ] – допускаемое нормальное напряжение, каждый материал имеет своё значение.
Чтобы обеспечить прочность конструкции, значение напряжения не должно превышать допускаемого, иначе может произойти разрушение материала.
Приблизительные значения допускаемого нормального напряжения для некоторых материалов:
Алюминий: [σ] = 30…100 МПа
Сталь 45: [σ] = 240…360 МПа
Легированные высококачественные стали: [σ] = 400 МПа и выше
Вольфрам: [σ] = 500 МПа
Рассмотрим касательное напряжение. Оно вычисляется по следующей формуле:
[τ] – допускаемое касательное напряжение, каждый материал имеет своё значение.
Для большинства материалов [τ] = 0,6•[σ]
Деформации и перемещения.
Деформация – это изменение формы и объёма тела.
Деформация бывает упругой и пластичной. При упругой деформации тело полностью восстанавливает свою первоначальную форму и размеры после снятия нагрузки, а при пластичной нагрузке этого не происходит.
Деформация также бывает линейной и угловой.
Расчёт на прочность при растяжении и сжатии.
Условие прочности при растяжении и сжатии – нормальное напряжение не должно превышать допускаемого значения.
Основное уравнение прочности при растяжении и сжатии выглядит следующим образом:
Расчёт на прочность при растяжении и сжатии можно также проводить через коэффициент запаса прочности
n – коэффициент запаса прочности
[n] – минимально допустимый коэффициент запаса прочности
При статической нагрузке [n] =1,5
Чтобы обеспечить прочность, должно соблюдаться условие:
Температурные напряжения.
При нагреве или охлаждении металлического стержня его длина изменяется. Удлинение от действия температуры вычисляется по формуле
где α – коэффициент температурного расширения, величина табличная.
Например, для стали α = 1,25·10 – 5 1/град
Δt – изменение температуры
В связи с нагревом или охлаждением в металлических конструкциях могут возникнуть дополнительные температурные напряжения. Вычислив удлинение от действия температуры, из формулы (3) можно вычислить температурные напряжения.
Монтажные напряжения.
Часто встречаются случаи, когда стержневые элементы конструкций изготавливаются короче или длиннее проектной длины. При монтаже конструкции такие стержни приходится растягивать или укорачивать, что приводит к возникновению дополнительных монтажных напряжений. Эти напряжения можно вычислить из формулы (3).
16. Сдвиг (основные понятия и определения), расчёт на прочность при сдвиге.
Сдвиг – это такой вид деформации, при котором в поперечном сечении бруса возникает следующий внутренний силовой фактор – поперечная сила Q.
Деформация сдвиг ещё называется срез.
При сдвиге действует касательное напряжения τ, которое вычисляется по следующей формуле
Деформация при сдвиге называется углом сдвига γ, вычисляется по следующей формуле
где G – модуль упругости ΙΙ рода, или модуль сдвига, характеризует жесткость бруса при сдвиге, величина табличная.
Для большинства материалов G = 0,4•E
Величина GS называется жёсткостью при сдвиге.
Подставим выражение (7) в выражение (8), получим
Выражения (9) и (10) являются законом Гука при сдвиге, который формулируется следующим образом: напряжение прямо пропорционально углу сдвига.
Единица измерения угла сдвига – радиан, можно перевести в градусы.
Условие прочности при сдвиге – касательное напряжение не должно превышать допускаемого значения.
Основное уравнение прочности при сдвиге выглядит следующим образом:
Примеры расчёта конструкций, работающих на сдвиг.
Рассмотрим заклёпочное соединение, на которое действуют сила F, направленная перпендикулярно осям заклёпок.
Условие прочности такого соединения имеет вид:
В данном случае Q =F;
S – площадь поперечного сечения всех заклёпок;
где S1 – площадь поперечного сечения одной заклёпки
Рассмотрим сварное соединение внахлёстку, на которое действует сила F.
Условие прочности такого соединения имеет вид:
В данном случае Q =F;
S – расчётная площадь сварного шва
где k – катет сварного шва
L – длина сварного шва по длине соединения
b – длина сварного шва по ширине соединения
Кинематические пары.
Примеры кинематических пар в зависимости от классов.
Кинематическая пара – соединение двух соприкасающихся звеньев, допускающее их относительное движение.
Элемент кинематическая пары – совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару
Кинематические пары различают и классифицируют по различным признакам.
1) По числу связей, налагаемых на относительное движение звеньев.
Всякое свободно движущееся в пространстве абсолютно твердое тело обладает шестью степенями свободы или шестью видами независимых возможных движений. Вхождение двух звеньев в кинематическую пару налагает на их относительное движение некоторые ограничения или условия связи; класс кинематической пары (номер класса совпадает с числом условий связи S) всегда находится в пределах от 1 до 5, число оставшихся подвижностей H дополняет число связей до шести, т.е. 
На рис. 3 представлены примеры кинематических пар 1 – 5 классов.
2) По характеру контакта звеньев различают пары низшие (требуемое относительное движение звеньев можно получить постоянным соприкасанием их элементов по поверхности) и высшие (требуемое относительное движение можно получить только соприкасанием их элементов по линиям и в точках). Например, трехподвижная пара по
рис. 3, в – низшая, а четырехподвижная по рис. 3, б – высшая.
3) По области относительного движения звеньев пары могут быть плоскими (траектории всех точек в относительном движении звеньев – плоские кривые, расположенные в параллельных плоскостях) и пространственными.
Плоская одноподвижная пара может быть либо вращательной (шарниром – рис. 3, д), либо поступательной (рис. 3, е); пространственная пара может быть, например, винтовой (одноподвижная), цилиндрической (двухподвижная), сферической (двух- и трехподвижная) и т.д.
Механизм, звенья которого образуют только вращательные, поступательные, цилиндрические и сферические пары, называют рычажным.
 |  |
| а – пятиподвижная пара (1 класс) | б – четырехподвижная пара (2 класс) |
 |  |
| в – трехподвижная пара (3 класс) | г – двухподвижная пара (4 класс) |
 |  |
| д – одноподвижная вращательная пара (5 класс) | е – одноподвижная поступательная пара (5 класс) |
| Рис. 3 |
Кинематические цепи.
Систему звеньев, связанных между собой кинематическими парами, называют кинематической цепью.
Классификация кинематических цепей
1) По области движения звеньев цепи бывают плоские (траектории движения точек всех звеньев –– плоские кривые, лежащие в параллельных плоскостях) и пространственные.
2) По признаку наличия разветвлений различают цепи простые (каждое звено цепи входит не более, чем в две кинематических пары) и сложные или разветвленные (некоторые звенья входят в три, или более пары); в разветвленных цепях могут присутствовать так называемые кратные (двойные, тройные и т.д.) шарниры.
3) По признаку наличия в кинематических цепях замкнутых контуров цепи могут быть замкнутыми и незамкнутыми; в замкнутой цепи каждое звено входит не менее, чем в две кинематические пары.
Некоторые дополнительные определения:
обобщенная координата механизма – каждая из независимых координат, определяющих положение всех звеньев механизма относительно стойки;
число степеней свободы (степень подвижности) механизма – число независимых вариаций обобщенных координат механизма;
начальное звено – звено, которому приписывается одна или несколько обобщенных координат механизма;
входное звено – звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев;
выходное звено – звено, совершающее движение, для выполнения которого предназначен механизм.
Примеры.
Методы силового анализа.
Силовой расчет механизмов без учета трения в кинематических парах допускает применение как аналитических, так и графо – аналитических методов.
В настоящем пособии предпочтение отдано графо – аналитическому методу планов сил.
Поскольку векторный план представляет собой графическое изображение векторного равенства, то при простой форме векторных силовых многоугольников их аналитическая обработка достаточно проста и позволяет рассчитать точные силовые соотношения для заданных положений механизмов.
Нагрузки (виды нагрузок, единицы измерения нагрузок).
Нагрузки – это внешние силы, действующие на конструкцию.
Сила – это мера механического воздействия одного тела на другое.
Единица измерения – ньютон (Н).
Также приблизительно можно принять:
1тонна =1000кг =10000Н =10кН
а) По длительности воздействия – постоянные, временные, переменные.
Б) По характеру приложения – распределённые и сосредоточенные.
В) По характеру воздействия – статические и динамические.
Статическая нагрузка медленно возрастает от нуля до своего конечного значения и остаётся постоянной в процессе работы детали или конструкции.
Динамическая нагрузка мгновенно возрастает от нуля до своего конечного значения и её значение непостоянно в процессе работы детали или конструкции.
Расчетные схемы.
При расчётах в сопромате для упрощения графической части реальные конструкции заменяются расчётными схемами, т.е. вместо чертежа детали или конструкции изображают упрощённую схему и по ней проводят расчёты.

