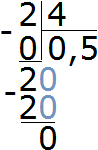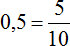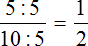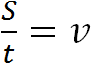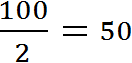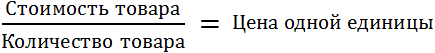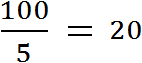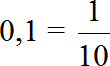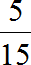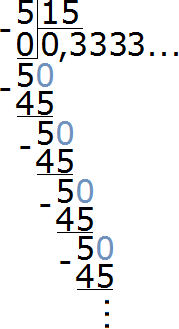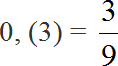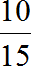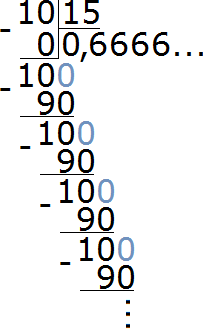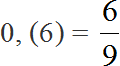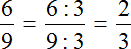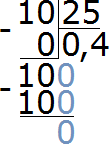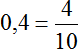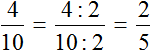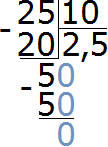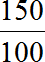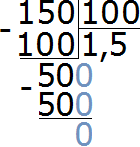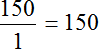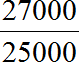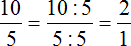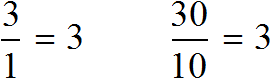в чем измеряется соотношение

Значение слова «соотношение»

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

Проще говоря, соотношение показывает для каждого количества чего-то одного сколько есть чего-то другого. Например, предположим, что у кого-то есть 8 апельсинов и 6 лимонов в вазе для фруктов, соотношение апельсинов и лимонов составит 4:3 (что эквивалентно 8:6), а соотношение лимонов и апельсинов составит 3:4. Кроме того, количество апельсинов относительно общего количества фруктов составит 4:7 (что эквивалентно 8:14). Соотношение 4:7 можно преобразовать в дробь 4/7, показывающую, какую долю от общего числа фруктов составляют апельсины.

СООТНОШЕ’НИЕ, я, ср. (книжн.). Взаимное отношение, связь между двумя или несколькими предметами или явлениями. Экономика и политика находятся в постоянном соотношении. С. спроса и предложения. С. борющихся сил.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

соотноше́ние

1. взаимное отношение; взаимная связь, зависимость ◆ Для меня достижимость желаемого (вещи ли, души ли) в обратном соотношении с желанностью его: чем желанней ― тем недостижимей. М. И. Цветаева, «Смерть Стаховича», 1919 г. (цитата из НКРЯ)

2. научн. мера относительной величины двух количеств ◆ В результате несколько снижается динамический диапазон сигнала, то есть соотношение самого высокого и самого низкого уровней, и плохо воспроизводятся крутые фронты. В. Хорт, «Информохранилища», 2008 г. // «Наука и жизнь» (цитата из НКРЯ) ◆ С гололёдом на улицах столицы много лет боролись, используя смесь песка и технической соли (обычное соотношение 92: 8). Александр Попов, «Ледниковый период», 2004 г. // «За рулем» (цитата из НКРЯ) ◆ Естественно, мы напрямую зависим от стабильности этой валюты, и вы прекрасно понимаете: соотношение, или курс, рубля к доллару ― это очень важно. Александр Гимельштейн, «Мы должны быть ответственны!», 2003 г. // «Восточно-Сибирская правда» (цитата из НКРЯ) ◆ Соотношение времени экспонирования ― 1: 2: 4: 8. Лев Быстров, «Цветное тоноразделение», 1974 г. // «Техника — молодежи» (цитата из НКРЯ) ◆ А оптимальное соотношение газов для роста водородных бактерий: 7 частей водорода, 2 части кислорода и 1 часть углекислого газа. Владимир Котелев, ««Водородный» белок — соперник «нефтяного»», 1974 г. // «Техника — молодежи» (цитата из НКРЯ)

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: абонент — это что-то нейтральное, положительное или отрицательное?

Источник

Единицы измерения и соотношение величин

Не все единицы измерения, приведенные в этом справочнике, применяются на практике. Д ругим цветом выделены величины, которые используются редко или вообще не используются.

Содержание

Единицы измерения длины

Сокращенные названия единиц длины в метрической системе измерения:

Таблица 1. Названия единиц измерения длины.

Чему равны единицы длины в метрической системе измерения

Основные единицы измерения длины равны:

Перевод крупных единиц длины в более мелкие :

1 км = 10 гкм = 100 дам = 1 000 м = 10 тыс. дм = 100 тыс. см = 1 млн мм

1 гкм = 10 дам = 100 м = 1 000 дм = 10 тыс. см = 100 тыс. мм

1 дам = 10 м = 100 дм = 1 000 см = 10 тыс. мм

1 м = 10 дм = 100 см = 1 000 мм

1 дм = 10 см = 100 мм

1 см = 10 мм

Соотношения единиц длины не метрических и метрической систем

1 дюйм (in) = 2,54 см

1 фут (ft) = 30, 48 см

1 ярд (yd) = 91,44 см

1 английская (американская)миля (ml) = 1 609,344 м

1 морская миля (nmi) = 1 852 м

Между собой эти не метрические единицы длины соотносятся следующим образом.

1 английская миля = 1760 ярдов = 5280 футов = 63360 дюймов

1 ярд = 3 фута = 36 дюймов

1 фут = 12 дюймов

Единицы измерения массы (веса)

Сокращенные названия единиц измерения массы (веса) в метрической системе измерения:

Таблица 2. Названия единиц измерения веса (массы).

Чему равны единицы массы (веса) в метрической системе мер

Основные единицы измерения веса (массы) равны:

Перевод крупных единиц массы (веса) в более мелкие :

1 т = 10 ц = 100 ст = 1 000 кг = 10 тыс. гг = 100 тыс. даг = 1 млн г = 10 млн дг = 100 млн сг = 1 млрд мг

1 ц = 10 ст = 100 кг = 1 000 гг = 10 тыс. даг = 100 тыс. г = 1 млн дг = 10 млн сг = 100 млн мг

1 ст = 10 кг = 100 гг = 1 000 даг = 10 тыс. г = 100 тыс. дг = 1 млн сг = 10 млн мг

1 кг = 10 гг = 100 даг = 1 000 г = 10 тыс. дг = 100 тыс. сг = 1 млн мг

1 гг = 10 даг = 100 г = 1 000 дг = 10 тыс. сг = 100 тыс. мг

1 даг = 10 г = 100 дг = 1 000 сг = 10 тыс. мг

1 г = 10 дг = 100 сг = 1 000 мг

1 дг = 10 сг = 100 мг

1 сг = 10 мг

Соотношения единиц длины не метрической английской и метрической международной систем

1 стоун (st) = 6,35 кг

1 фунт (lb) = 453,59 г

1 унция (oz) = 28,35 г

Между собой единицы веса (массы) английской системы мер имеют такие соотношения.

1 стоун = 14 фунтов = 224 унции

1 фунт = 16 унций

Единицы измерения площади

Сокращенные названия единиц измерения площади:

Таблица 3. Названия единиц измерения площади.

Чему равны единицы площади в метрической системе

Основные единицы измерения площади:

Перевод крупных единиц измерения площади в более мелкие :

1 км 2 = 100 га = 10 тыс. а = 1 млн м 2 = 100 млн дм 2 = 10 млрд см 2 = 1 трлн мм 2

1 га = 100 а = 10 тыс. м 2 = 1 млн дм 2 = 100 млн см 2 = 10 млрд мм 2

1 а = 100 м 2 = 10 тыс. дм 2 = 1 млн см 2 = 100 млн мм 2

1 м 2 = 100 дм 2 = 10 тыс. см 2 = 1 млн мм 2

1 дм 2 = 100 см 2 = 10 тыс. мм 2

1 см 2 = 100 мм 2

Соотношения единиц измерения площади не метрической английской и метрической международной систем

1 квадратная миля (миля 2 ) = 2,59 км 2

1 акр = 4046,86 м 2

1 руд = 1011,71 м 2

1 род 2 = 25,293 м 2

1 ярд 2 = 0,83613 м 2

1 фут 2 = 929,03 см 2

1 дюйм 2 = 6,4516 см 2

Между собой единицы площади английской системы мер имеют такие соотношения.

1 квадратная миля (миля 2 ) = 640 акр = 2 560 руд = 102 400 род 2 = 3 097 600 ярд 2 = 27 878 400 фут 2 = 4 014 489 600 дюйм 2

1 акр = 4 руд = 160 род 2 = 4 840 ярд 2 = 43 560 фут 2 = 6 272 640 дюйм 2

1 руд = 40 род 2 = 1 210 ярд 2 = 10 890 фут 2 = 1 568 160 дюйм 2

1 род 2 = 30,25 ярд 2 = 272,25 фут 2 = 39 204 дюйм 2

1 ярд 2 = 9 фут 2 = 1296 дюйм 2

1 фут 2 = 144 дюйм 2

Единицы измерения объема

Сокращенные названия единиц измерения объема:

Таблица 4. Единицы измерения объма.

Чему равны единицы объема в метрической системе

Основные единицы объема:

Перевод крупных единиц измерения объема в более мелкие :

1 м 3 = 1 000 дм 3 = 1 млн см 3 = 1 млрд мм 3

1 дм 3 = 1 000 см 3 = 1 000 000 мм 3

1 см 3 = 1 000 мм 3

Соотношения единиц измерения объема не метрической английской и метрической международной систем

1 кубический дюйм (cu in) ≈ 16,3871 см 3

1 кубический фут (cu ft) ≈ 0,02832 м 3

1 кубический ярд (cu ya) ≈ 0,76456 м 3

Между собой единицы объема английской системы мер имеют такие соотношения.

1 кубический ярд = 27 кубических футов = 46 656 кубических дюймов

1 кубический фут = 1 728 кубических дюймов

Единицы мер объема жидкостей, сыпучих тел и вместимости сосудов

Сокращенные названия единиц измерения объема жидкостей, сыпучих тел и вместимости сосудов:

Таблица 5. Название единиц измерения объема жидкостей.

Чему равны единицы объема жидкостей, сыпучих тел и вместимости сосудов

Чему равны некоторые единиц измерения объема жидкостей, сыпучих тел и вместимости сосудов в не метрической английской системе

1 британская пинта (British pint) ≈ 0,57 л

1 британский галлон (British gallon) ≈ 4.54609188 л

1 галлон США (US gallon) ≈ 3.785411784 л

1 британский баррель (British barrel) ≈ 163,65 л

1 баррель США (US barrel) ≈ 158,987 л

Единицы измерения скорости

Сокращенные названия единиц измерения скорости:

Таблица 6. Названия единиц измерения скорости.

Чему равны единицы измерения скорости

Основные единицы измерения скорости:

Перевод крупных единиц измерения скорости в более мелкие :

1 км/с = 60 км/мин = 1 000 м/с = 3 600 км/ч = 60 000 м/мин = 3 600 000 м/ч

1 км/мин ≈ 16,67 м/с = 60 км/ч = 1 000 м/мин = 60 000 м/ч

1 м/с = 3,6 км/ч = 60 м/мин = 3 600 м/ч

1 км/ч ≈ 16,667 м/мин = 1 000 м/ч

1 м/мин = 60 м/ч

Единица измерения скорости в навигации

1 узел = 1 морская миля/час = 1,852 км/ч = 1852 м/ч

Единицы измерения времени

Сокращенные названия основных единиц времени:

Таблица 7. Основные единицы измерения времени.

Соотношение основных единиц измерения времени

Единицы измерения времени в рамках суток:

Перевод крупных единиц измерения времени в более мелкие :

1 сут = 24 ч = 1 440 мин = 86 400 сек

1 ч = 60 мин = 3 600 сек

1 мин = 60 сек

Другие единицы измерения времени

В сторону уменьшения:

1 сек = 10 дс = 100 сс = 1 000 мс

Источник

Соотношение и пропорция

Основой математических исследований является возможность получить знание об определённых величинах, сравнивая их с другими величинами, которые либо равны, либо больше или меньше, чем те которые являются предметом исследования. Это обычно производится с помощью ряда уравнений и пропорций. Когда мы используем уравнения, то мы определяем искомую величину, находя её равенство с какой-то другой уже знакомой величиной или величинами.

Однако, часто бывает, что мы сравниваем неизвестную величину с другими, которые не равны ей, а больше или меньше её. Здесь нужен другой подход к обработке данных. Нам может понадобиться узнать, например, на сколько одна величина больше чем другая, или сколько раз одна содержит другую. Для нахождения ответа на эти вопросы мы узнаем что такое соотношение двух величин. Одно соотношение называется арифметическим, а другое геометрическим. Хоть и стоит заметить, что оба эти термина не были приняты случайно или только в целях отличия. Как арифметическое, так и геометрическое соотношения применимы как к арифметике, так и к геометрии.

Являясь компонентом обширного и важного предмета, пропорция зависит от соотношений, поэтому необходимо чёткое и полное понимание этих понятий.

344. Если из этих трёх значений: антецедента, консеквента и соотношения даны любые два, то третье можно найти.

Соотв. 1. Если у двух пар антецеденты и консеквенты равны, то их соотношения тоже равны.

Соотв. 2. Если у двух пар соотношения и антеценденты равны, то и консеквенты равны и если соотношения и консеквенты равны, то и антецеденты равны.

345. Если две сравниваемые величины равны, то их соотношение равно единице или соотношению равенства. Соотношение 3*6:18 равно единице, так как частное любой величины разделённой на саму себя равно 1.

Если антецедент пары больше, чем консеквент, то соотношение больше единицы. Так как делимое больше, чем делитель, то частное больше единицы. Так соотношение 18:6 равно 3. Это называется соотношение большего неравенства.

С другой стороны, если антецедент меньше, чем консеквент, то соотношение меньше единциы и это называется соотношением меньшего неравенства. Так соотношение 2:3 меньше единицы, потому что делимое меньше делителя.

Отсюда обратное соотношение выражается путём инвертирования дроби, которая отображает прямое соотношение, либо, когда запись ведётся с помощью точек, инвертируя порядок записи членов.
Таким образом a относится к b обратно тому, как b к a.

347. Сложное соотношение это соотношение произведений соответствующих членов с двумя и более простыми соотношениями.
Так соотношение 6:3, равно 2
И соотношение 12:4, равно 3
Составленное из них соотношение 72:12 = 6.

Таким же образом все величины, которые являются и антецедентами и консеквентами исчезнут, когда произведение дробей будет упрощено до своих младших членов и в остатке сложное соотношение будет выражаться первым антецедентом и последним консеквентом.

349. Особый класс сложных соотношений получается при умножении простого соотношения на самого себя или на другое равное соотношение. Эти соотношения называются двойными, тройными, четверными, и так далее, в соответствии с количеством операций умножения.

Соотношение, составленное из двух равных соотношений, то есть, квадрата простого соотношения, называют двойным соотношением.

Составленное из трёх, то есть, куб простого соотношения, называют тройным, и так далее.

350. Для того, чтобы величины можно соотнести друг с другом, они должны быть одинакового рода, так, чтобы можно было с уверенностью утверждать равны ли они между собой, или одна из них больше или меньше. Фут относится к дюйму, как 12 к 1: он в 12 раз больше, чем дюйм. Но нельзя, например, сказать, что час длиннее или короче, чем палка, или акр больше или меньше, чем градус. Однако, если эти величины выражены в числах, то может существовать соотношение между этими числами. То есть может существовать соотношение между количеством минут в часе и количеством шагов в миле.

Соотв. При известном консеквенте, чем больше антецедент, тем больше соотношение, и, наоборот, чем больше соотношение, тем больше антецедент.

Соотв. При данном антецеденте, чем больше консеквент, тем меньше соотношение. И наоборот, чем больше соотношение, тем меньше консеквент.

354. Из двух последних статей следует, что умножение антецедента пары на любую величину окажет такой же эффект на соотношение, как деление консеквента на эту величину, а деление антецедента, окажет такой же эффект, как умножение консеквента.
Поэтому соотношение 8:4, равно 2
Умножая антецедент на 2, соотношение 16:4 равно 4
Разделив антецедент на 2, соотношение 8:2 равно 4.

Соотв. Любой множитель или делитель может быть перенесён от антецедента пары к консеквенту или от консеквента к антецеденту без изменения соотношения.

355. Как очевидно из Статей. 352 и 353, если антецедент и консеквент оба умножить или разделить на одну и ту же величину, то соотношение не меняется.

Соотв. 1. Соотношение двух дробей, у которых есть общий знаменатель, такое же как отношение их числителей.
Таким образом соотношение a/n:b/n, то же самое, что и a:b.

Соотв. 2. Прямое соотношение двух дробей, у которых есть общий числитель, равно обратному соотношению их знаменателей.

Доказательство.

Соотношение разницы антецедентов к разнице консеквентов также одинаковое.

358. Если в нескольких парах соотношения равны, то сумма всех антецедентоа относится к сумме всех консеквентов, как любой антецедент к своему консеквенту.
Таким образом соотношение
|12:6 = 2
|10:5 = 2
|8:4 = 2
|6:3 = 2
Таким образом соотношение (12 + 10 + 8 + 6):(6 + 5 + 4 + 3) = 2.

Так как последний числитель больше, чем другой, то соотношение больше.
Если вместо добавления ту же самую величину отнять от двух членов, то очевидно, что эффект на соотношение будет обратным.

Примеры.

1. Что больше: соотношение 11:9, или соотношение 44:35?

3. Если антецедент пары равен 65, а соотношение равно 13, то какой консеквент?

4. Если консеквент пары равен 7, и соотношение равно 18, то какой антецедент?

5. Как выглядит сложное соотношение составленное из 8:7, и 2a:5b, а также (7x+1):(3y-2)?

9. Каково соотношение сложенное из 7:5, и удвоенного соотношения 4:9, и утроенного соотношения 3:2?
Отв. 14:15.

Источник

Соотношения

Соотношением называют некоторую взаимосвязь между сущностями нашего мира. Это могут быть числа, физические величины, предметы, продукты, явления, действия и даже люди.

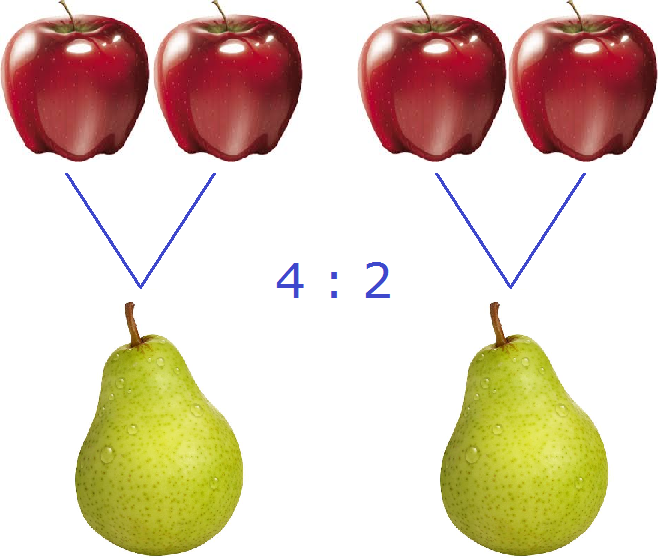
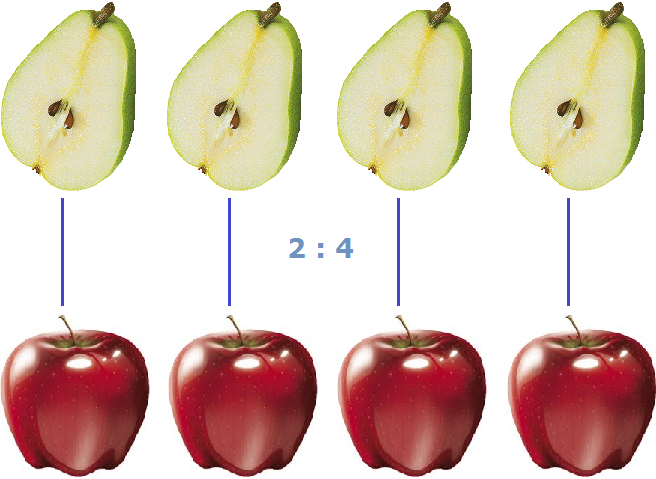
В повседневной жизни, когда речь заходит о соотношениях, мы говорим «соотношения того-то и того-то». Например, если в вазе лежит 4 яблока и 2 груши, то мы говорим «соотношения яблок и груш» или если поменять местами яблоки и груши, то «соотношения груш и яблок».

В математике соотношение чаще употребляется как «отношение того-то к тому-то». Например, соотношение четырёх яблок и двух груш, которые мы рассматривали выше, в математике будет читаться как «отношение четырех яблок к двум грушам» или если поменять местами яблоки и груши, то «отношение двух груш к четырем яблокам».

Запишем соотношение четырех яблок и двух груш с помощью символа соотношения:

Это соотношение можно прочитать как «четыре к двум» либо «соотношение четырех яблок и двух груш» либо «четыре яблока относится к двум грушам»

В дальнейшем соотношение мы будем называть просто отношением.

Что такое отношение?

Отношением в математике называют частное двух чисел.

Данное отношение представляет собой деление числа 4 на число 2. Если выполнить это деление, мы получим ответ на вопрос сколько яблок приходится на единицу груши

Получили 2. Значит четыре яблока и две груши (4 : 2) соотносятся (взаимосвязаны друг с другом) так, что на одну грушу приходится два яблока

На рисунке показано, как четыре яблока и две груши соотносятся между собой. Видно, что на каждую грушу приходятся два яблока.

Чтобы найти значение дроби нужно вспомнить, как делить меньшее число на большее

Получили 0,5. Переведём эту десятичную дробь в обыкновенную:

Сократим полученную обыкновенную дробь на 5

Получили ответ (половину груши). Значит две груши и четыре яблока (2 : 4) соотносятся (взаимосвязаны друг с другом) так, что на одно яблоко приходится половина груши

На рисунке показано, как две груши и четыре яблока соотносятся между собой. Видно, что на каждое яблоко приходится половинка груши.

Числа, из которых составлено отношение, называют членами отношения. Например, в отношении 4 : 2 членами являются числа 4 и 2.

Рассмотрим другие примеры соотношений. Для приготовления чего-либо составляется рецепт. Рецепт строят из соотношений между продуктами. Например, для приготовления овсяной каши обычно требуется стакан хлопьев на два стакана молока или воды. Получается соотношение 1 : 2 («один к двум» или «один стакан хлопьев на два стакана молока»).

Если перевернуть соотношение 1 : 2 то получится соотношение 2 : 1 («два к одному» или «два стакана молока на один стакан хлопьев»). Преобразуем соотношение 2 : 1 в дробь, получим . Вычислив эту дробь, получим 2. Значит два стакана молока и один стакан хлопьев соотносятся (взаимосвязаны друг с другом) так, что на один стакан хлопьев приходятся два стакана молока.

Пример 2. В классе 15 школьников. Из них 5 – это мальчики, 10 – девочки. Можно записать соотношение девочек и мальчиков 10 : 5 и преобразовать это соотношение в дробь . Вычислив эту дробь получим 2. То есть девочки и мальчики соотносятся между собой так, что на каждого мальчика приходятся две девочки

На рисунке показано, как десять девочек и пять мальчиков соотносятся между собой. Видно, что на каждого мальчика приходятся две девочки.

Соотношение не всегда можно обращать в дробь и находить частное. В некоторых случаях это будет нелогично.

Так, если перевернуть отношение получится , а это уже отношение мальчиков к девочкам. Если вычислить эту дробь получается 0,5. Получается, что пять мальчиков относятся к десяти девочкам так, что на каждую девочку приходится половина мальчика. Математически это конечно верно, но с точки зрения реальности не совсем разумно, ибо мальчик это живой человек и его нельзя просто так взять и разделить, как грушу или яблоко.

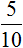
Умение построить правильное отношение — важный навык при решении задач. Так в физике, отношение пройденного расстояния ко времени есть скорость движения.

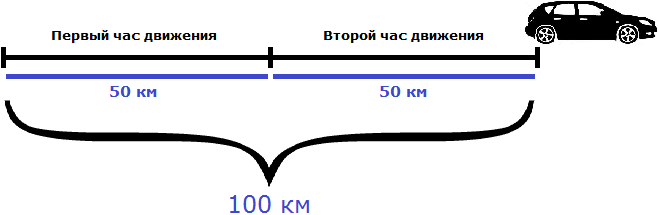
Предположим, что автомобиль проехал 100 километров за 2 часа. Тогда отношение пройденных ста километров к двум часам будет скоростью движения автомобиля:

Скоростью принято называть расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. А отношение, как было сказано ранее, позволяет узнать сколько количества одной сущности приходится на единицу другой. В нашем примере отношение ста километров к двум часам показывает сколько километров приходится на один час движения. Видим, что на каждый час движения приходятся 50 километров

Пример 2. Отношение стоимости товара к его количеству есть цена одной единицы товара

Если мы взяли в магазине 5 шоколадных батончиков и их общая стоимость составила 100 рублей, то мы можем определить цену одного батончика. Для этого нужно найти отношение ста рублей к количеству батончиков. Тогда получим, что на один батончик приходятся 20 рублей

Сравнение величин

Ранее мы узнали, что отношение между величинами разной природы образуют новую величину. Так, отношение пройденного расстояния ко времени есть скорость движения. Отношение стоимости товара к его количеству есть цена одной единицы товара.

Но отношение можно использовать и для сравнения величин. Результат выполнения такого отношения есть число, показывающее во сколько раз первая величина больше второй или какую часть первая величина составляет от второй.

Чтобы узнать во сколько раз первая величина больше второй, в числитель отношения нужно записать большую величину, а в знаменатель меньшую величину.

Чтобы узнать какую часть первая величина составляет от второй, в числитель отношения нужно записать меньшую величину, а в знаменатель большую величину.

Рассмотрим числа 20 и 2. Давайте узнаем во сколько раз число 20 больше числа 2. Для этого находим отношение числа 20 к числу 2. В числителе отношения записываем число 20, а в знаменателе — число 2

Значение данного отношения равно десяти

Отношение числа 20 к числу 2 есть число 10. Это число показывает во сколько раз число 20 больше числа 2. Значит число 20 больше числа 2 в десять раз.

Пример 2. В классе 15 школьников. 5 из них это мальчики, 10 – девочки. Определить во сколько раз девочек больше мальчиков.

Записываем отношение девочек к мальчикам. В числителе отношения записываем количество девочек, в знаменатель отношения — количество мальчиков:

Значение данного отношения равно 2. Значит в классе из 15 человек девочек в два раза больше мальчиков.

Здесь уже не стоит вопрос о том, сколько девочек приходятся на одного мальчика. В данном случае отношение используется для сравнения количества девочек с количеством мальчиков.

Пример 3. Какую часть число 2 составляет от числа 20.

Находим отношение числа 2 к числу 20. В числителе отношения записываем число 2, а в знаменателе — число 20

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее

Значение отношения числа 2 к числу 20 есть число 0,1

В данном случае десятичную дробь 0,1 можно перевести в обыкновенную. Такой ответ будет проще для восприятия:

Значит число 2 от числа 20 составляет одну десятую часть.

Можно сделать проверку. Для этого найдём от числа 20. Если мы всё сделали правильно, то должны получить число 2

Получили число 2. Значит одна десятая часть от числа 20 есть число 2. Отсюда делаем вывод, что задача решена верно.

Пример 4. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества школьников составляют мальчики.

Записываем отношение мальчиков к общему количеству школьников. В числителе отношения записываем пять мальчиков, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 5 нужно разделить на число 15

При делении 5 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную

Сократим полученную дробь на 3

Получили окончательный ответ . Значит мальчики составляют одну треть от всего класса

На рисунке видно, что в классе из 15 школьников треть класса составляют 5 мальчиков.

Если для проверки найти от 15 школьников, то мы получим 5 мальчиков

Записываем отношение числа 35 к числу 5. В числитель отношения нужно записать число 35, в знаменатель — число 5, но не наоборот

Значение данного отношения равно 7. Значит число 35 в семь раз больше числа 5.

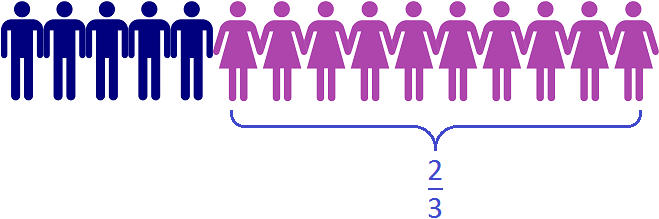
Пример 6. В классе 15 человек. 5 из них это мальчики, 10 – девочки. Определить какую часть от общего количества составляют девочки.

Записываем отношение девочек к общему количеству школьников. В числителе отношения записываем десять девочек, в знаменателе — общее количество школьников. Общее количество школьников это 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения записываем число 15

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае, число 10 нужно разделить на число 15

При делении 10 на 15 получается периодическая дробь. Переведём эту дробь в обыкновенную

Сократим полученную дробь на 3

На рисунке видно, что в классе из 15 школьников две трети класса составляют 10 девочек.

Если для проверки найти от 15 школьников, то получим 10 девочек

Пример 7. Какую часть 10 см составляют от 25 см

Записываем отношение десяти сантиметров к двадцати пяти сантиметрам. В числителе отношения записываем 10 см, в знаменателе — 25 см

Чтобы найти значение данного отношения, нужно вспомнить, как делить меньшее число на большее. В данном случае число 10 нужно разделить на число 25

Переведём полученную десятичную дробь в обыкновенную

Сократим полученную дробь на 2

Получили окончательный ответ . Значит 10 см составляют от 25 см.

Пример 8. Во сколько раз 25 см больше 10 см

Записываем отношение двадцати пяти сантиметров к десяти сантиметрам. В числителе отношения записываем 25 см, в знаменателе — 10 см

Найдём значение данного отношения

Получили ответ 2,5. Значит 25 см больше 10 см в 2,5 раза (в два с половиной раза)

Важное замечание. При нахождении отношения одноименных физических величин эти величины обязательно должны быть выражены в одной единице измерения, в противном случае ответ будет неверным.

Например, если мы имеем дело с двумя длинами и хотим узнать во сколько раз первая длина больше второй или какую часть первая длина составляет от второй, то обе длины сначала нужно выразить в одной единице измерения.

Пример 9. Во сколько раз 150 см больше 1 метра?

Сначала сделаем так, чтобы обе длины были выражены в одной единице измерения. Для этого переведем 1 метр в сантиметры. Один метр это сто сантиметров

1 м = 100 см

Теперь находим отношение ста пятидесяти сантиметров к ста сантиметрам. В числителе отношения записываем 150 сантиметров, в знаменателе — 100 сантиметров

Найдём значение данного отношения

Получили ответ 1,5. Значит 150 см больше 100 см в 1,5 раза (в полтора раза).

А если бы не стали переводить метры в сантиметры и сразу попытались найти отношение 150 см к одному метру, то у нас получилось бы следующее:

Получилось бы, что 150 см больше одного метра в сто пятьдесят раз, а это неверно. Поэтому обязательно нужно обращать внимание на единицы измерения физических величин, которые участвуют в отношении. Если эти величины выражены в разных единицах измерения, то для нахождения отношения этих величин, нужно перейти к одной единице измерения.

Пример 10. В прошлом месяце зарплата человека составляла 25000 рублей, а в текущем месяце зарплата выросла до 27000 рублей. Определить во сколько раз выросла зарплата

Записываем отношение двадцати семи тысяч к двадцати пяти тысячам. В числителе отношения записываем 27000, в знаменателе — 25000

Найдём значение данного отношения

Получили ответ 1,08. Значит зарплата выросла в 1,08 раза. В будущем, когда мы познакомимся с процентами, такие показатели как зарплата будем выражать в процентах.

Пример 11. Ширина многоквартирного дома 80 метров, а высота 16 метров. Во сколько раз ширина дома больше его высоты?

Записываем отношение ширины дома к его высоте:

Значение данного отношения равно 5. Значит ширина дома в пять раз больше его высоты.

Свойство отношения

Отношение не изменится если его члены умножить или разделить на одно и тоже число.

Это одно из важнейших свойств отношения следует из свойства частного. Мы знаем, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится. А поскольку отношение является ничем иным как делением, то свойство частного работает и для него.

В нашем примере удобнее разделить члены отношения на их наибольший общий делитель (НОД).

НОД членов 10 и 5 это число 5. Поэтому можно разделить члены отношения на число 5

Получили новое отношение . Это есть отношение два к одному (2:1). Данное отношение, как и прошлое отношение 10:5 показывает, что на одного мальчика приходятся две девочки.

На рисунке показано отношение 2 : 1 (два к одному). Как и в прошлом отношении 10 : 5 на одного мальчика приходятся две девочки. Другими словами, отношение не изменилось.

Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз в первом классе девочек больше мальчиков? Во сколько раз во втором классе девочек больше мальчиков?

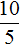
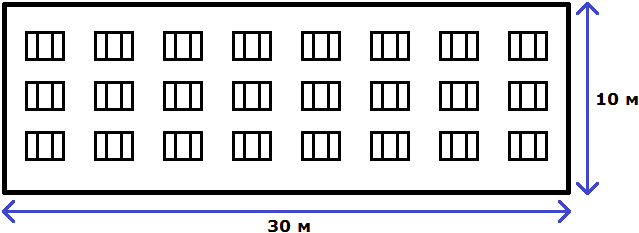
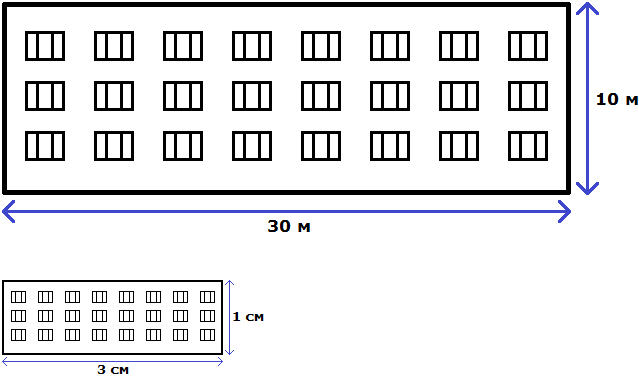
В обоих классах девочек в два раза больше мальчиков, поскольку отношения и равны одному и тому же числу.

Свойство отношения позволяет строить различные модели, которые имеют схожие параметры с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 метров и высоту 10 метров.

Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров

3 м = 300 см

1 м = 100 см

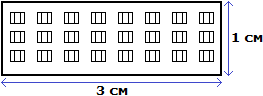
Имеем отношение 300 см : 100 см. Разделим члены этого отношения на 100. Получим отношение 3 см : 1 см. Теперь можно нарисовать дом с шириной 3 см и высотой 1 см

Конечно нарисованный дом намного меньше реального дома, но неизменным осталось отношение ширины и высоты. Это позволило нам нарисовать дом, максимально похожий на реальный

Отношение можно понимать и другим образом. Изначально было сказано, что у реального дома ширина составляет 30 метров, а высота 10 метров. Итого получается 30+10, то есть 40 метров.

Эти 40 метров можно понимать, как 40 частей. Отношение 30 : 10 говорит о том, что 30 частей приходится на ширину, а 10 частей на высоту.

Далее члены отношения 30 : 10 были разделены на 10. В результате получилось отношение 3 : 1. Это отношение можно понимать, как 4 части, три из которых приходится на ширину, одна — на высоту. В этом случае обычно требуется узнать сколько конкретно метров приходится на ширину и высоту.

Другими словами, нужно узнать сколько метров приходится на 3 части и сколько метров приходится на 1 часть. Сначала надо узнать сколько метров приходится на одну часть. Для этого общие 40 метров нужно разделить на 4, поскольку в отношении 3 : 1 всего четыре части

Далее с помощью умножения определяют сколько метров приходятся на ширину и высоту. Члены, которые даны в отношении используют в качестве сомножителя.

Определим сколько метров приходится на ширину:

Определим сколько метров приходится на высоту:

Несколько членов отношения

Если в отношении дано несколько членов, то их можно понимать как части от чего-либо.

Отношение 2 : 1 : 3 говорит о том, что мама получила 2 части, папа — 1 часть, дочка — 3 части. Другими словами, каждый член отношения 2 : 1 : 3 это определенная часть от 18 яблок:

Узнаем сколько яблок приходится на одну часть. Для этого 18 яблок разделим на 6

18 : 6 = 3 (яблока на одну часть)

Узнаем сколько яблок получила мама:

Узнаем сколько яблок получил папа:

Узнаем сколько яблок получила дочка:

4 килограмма нового серебра будет содержать 3 части никеля, 4 части цинка и 13 частей меди. Сначала узнаем сколько всего частей будет в четырех килограммах серебра:

3 + 4 + 13 = 20 (частей)

Определим сколько килограммов будет приходиться на одну часть:

Определим сколько килограммов никеля будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что три части сплава содержат никель. Поэтому умножаем 0,2 на 3:

0,2 кг × 3 = 0,6 кг никеля

Теперь определим сколько килограммов цинка будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что четыре части сплава содержат цинк. Поэтому умножаем 0,2 на 4:

0,2 кг × 4 = 0,8 кг цинка

Теперь определим сколько килограммов меди будет содержáться в 4 кг нового серебра. В отношении 3 : 4 : 13 указано, что тринадцать частей сплава содержат медь. Поэтому умножаем 0,2 на 13:

0,2 кг × 13 = 2,6 кг меди

Значит, чтобы получить 4 кг нового серебра, нужно взять 0,6 кг никеля, 0,8 кг цинка и 2,6 кг меди.

Определим сколько граммов сплава приходится на одну часть. В условии сказано, что для изготовления куска латуни требуется 120 г меди. Также сказано, что три части сплава содержат медь. Если разделить 120 на 3, мы узнаем сколько граммов сплава приходится на одну часть:

120 : 3 = 40 граммов на одну часть

Теперь определим сколько требуется цинка для изготовления куска латуни. Для этого 40 граммов умножим на 2, поскольку в отношении 3 : 2 указано, что две части содержат цинк:

40 г × 2 = 80 граммов цинка

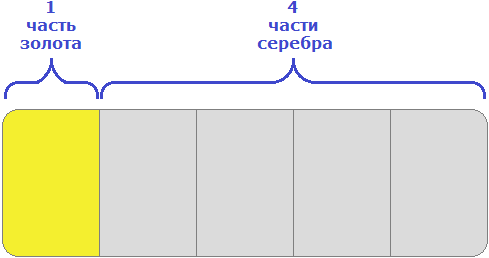
Пример 4. Взяли два сплава золота и серебра. В одном количество этих металлов находится в отношении 1 : 9, а в другом 2 : 3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, в котором золото и серебро относилось бы как 1 : 4?

Решение

15 кг нового сплава должны состоять в отношении 1 : 4. Это отношение говорит о том, что на одну часть сплава будет приходиться золото, а на четыре части будет приходиться серебро. Всего же частей пять. Схематически это можно представить следующим образом

Определим массу одной части. Для этого сначала сложим все части (1 и 4), затем массу сплава разделим на количество этих частей

1 + 4 = 5
15 кг : 5 = 3 кг

Одна часть сплава будет иметь массу 3 кг. Тогда в 15 кг нового сплава будет содержáться 3 × 1 = 3 кг золота и серебра 3 × 4 = 12 кг серебра.

Поэтому для получения сплава массой 15 кг нам нужно 3 кг золота и 12 кг серебра.

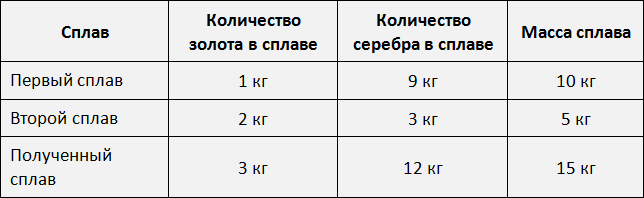
Теперь ответим на вопрос задачи — « Сколько нужно взять каждого сплава? »

Первого сплава мы возьмем 10 кг, поскольку золото и серебро в нём находятся в отношении 1 : 9. То есть этот первый сплав даст нам 1 кг золота и 9 кг серебра.

Второго сплава мы возьмем 5 кг, поскольку золото и серебро находятся в нём в отношении 2 : 3. То есть этот второй сплав даст нам 2 кг золота и 3 кг серебра.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник