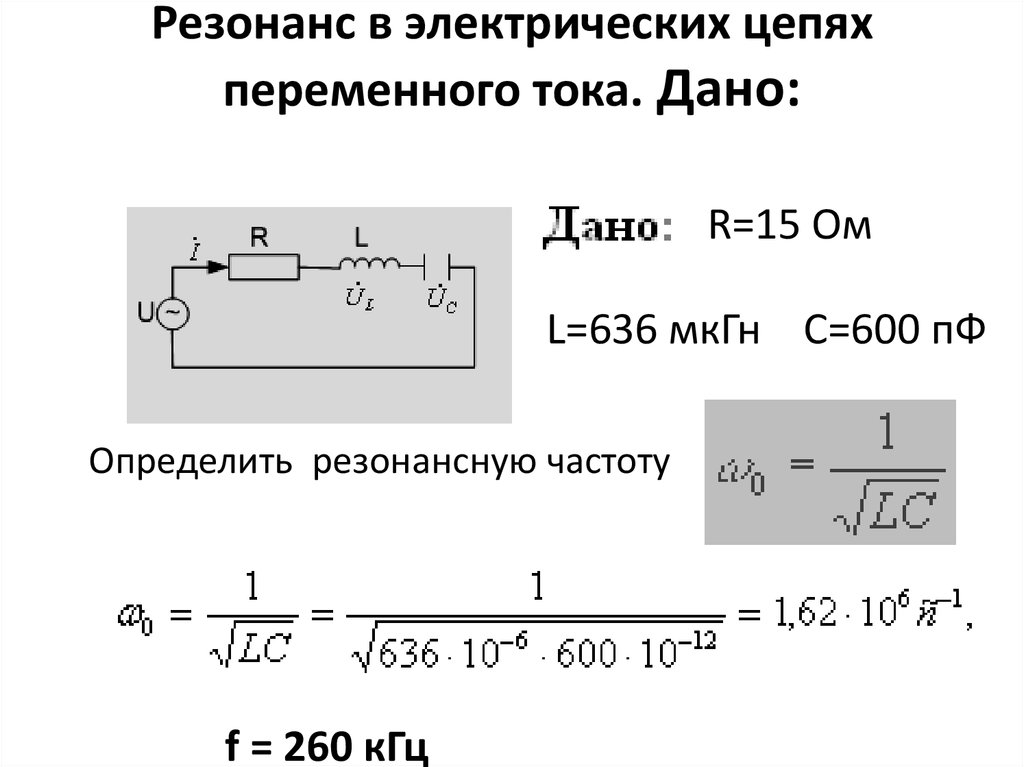
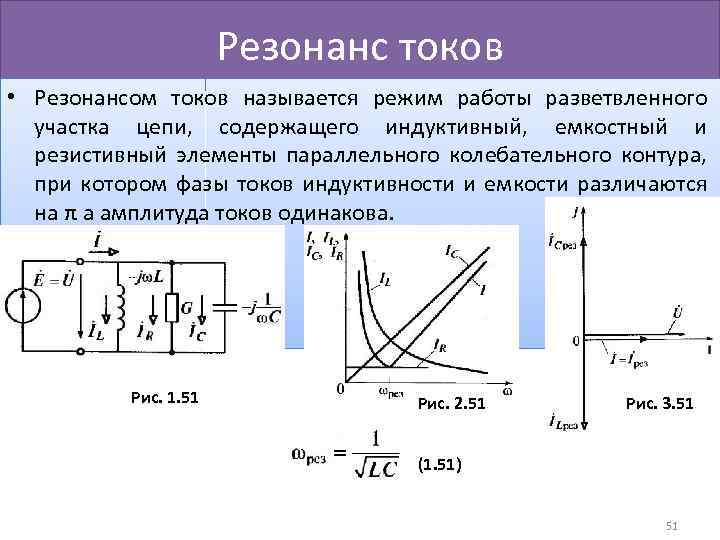
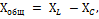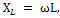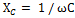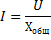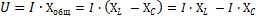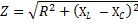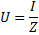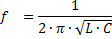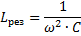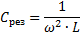в чем измеряется резонанс напряжений
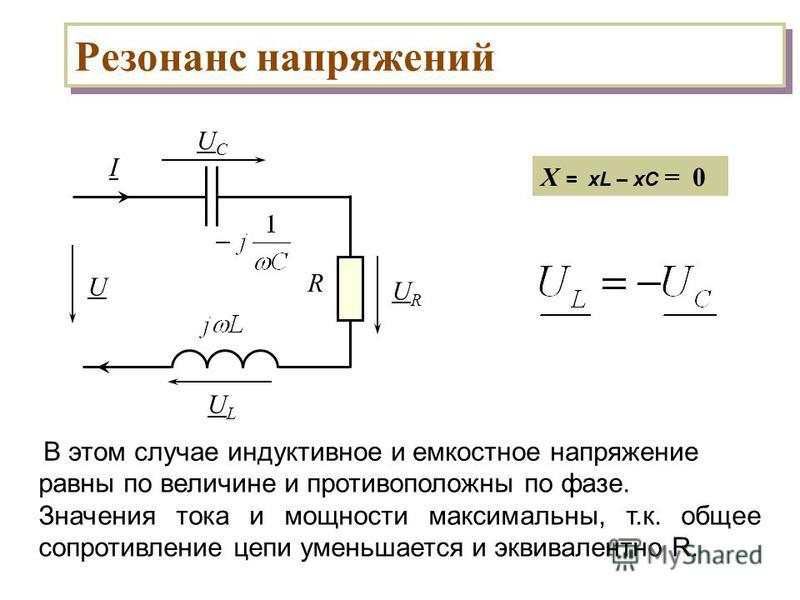
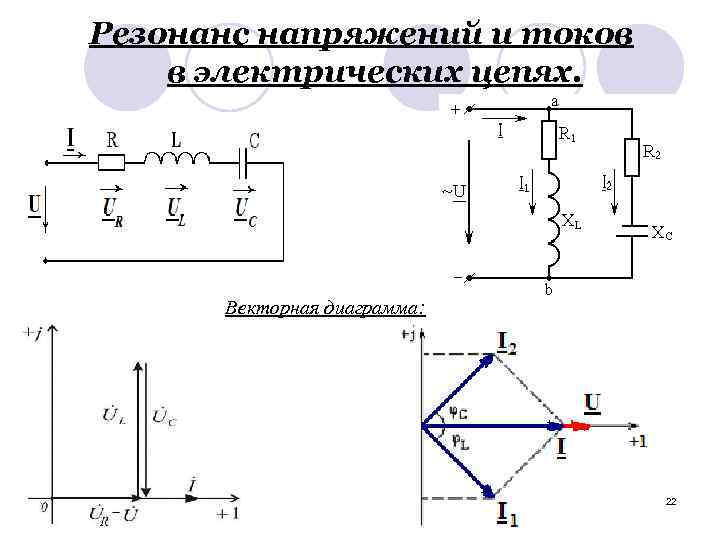
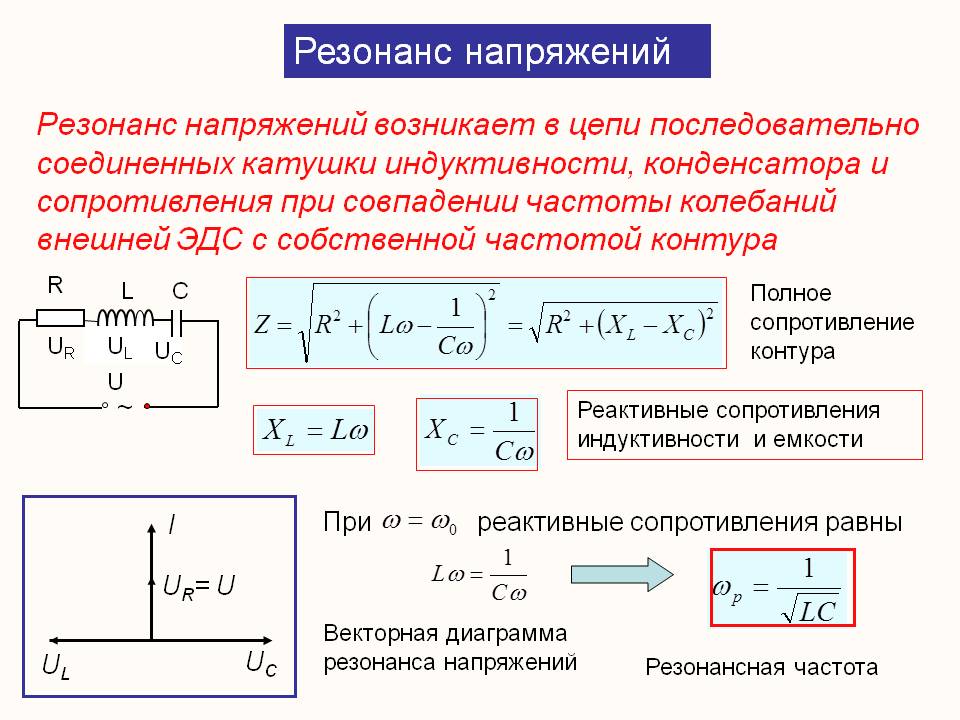
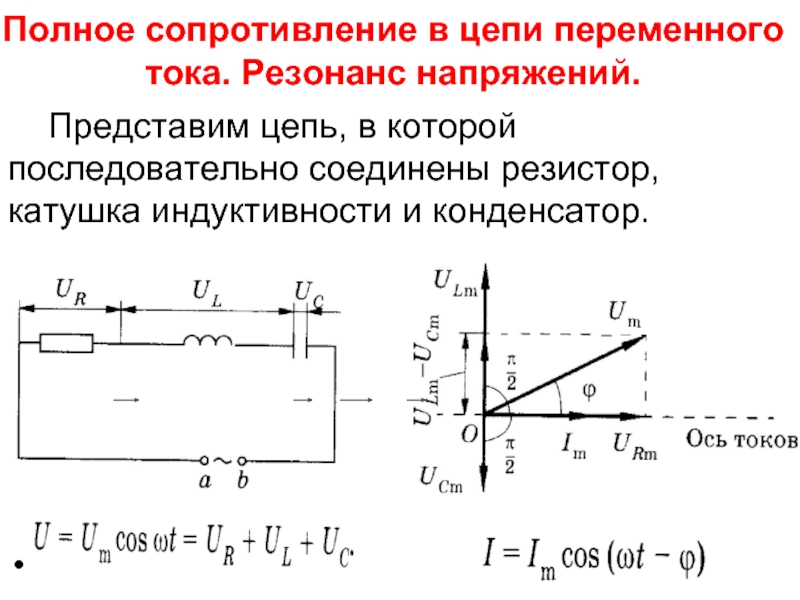
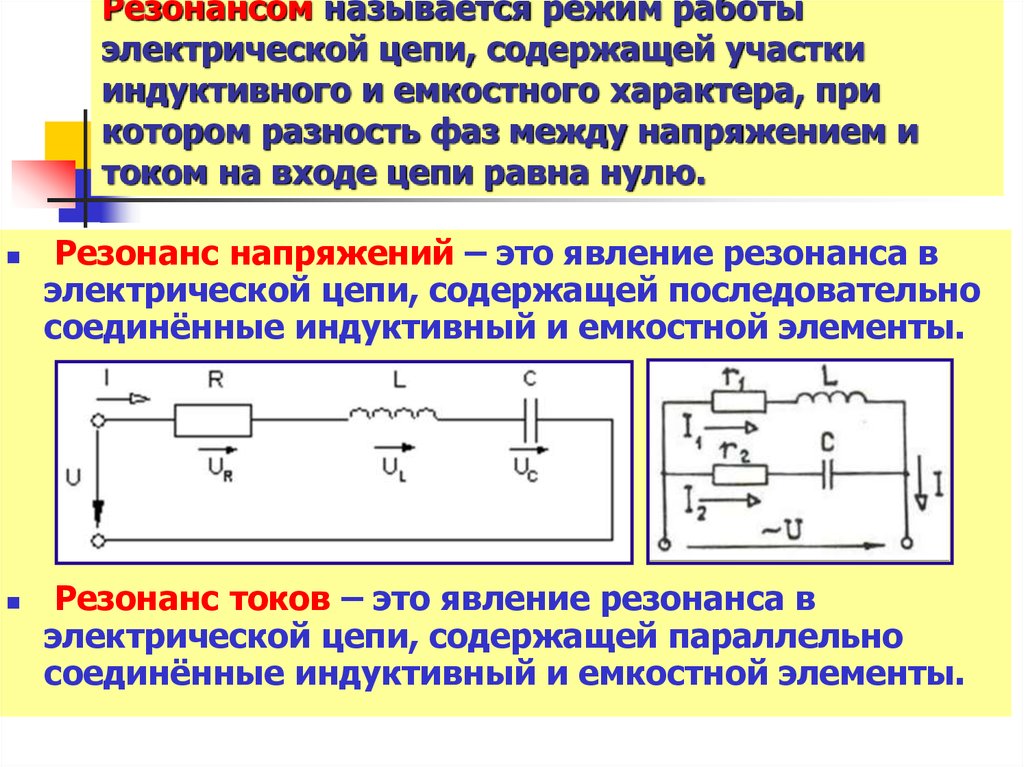
Резонанс напряжений
Катушка индуктивности вносит сдвиг фаз, при котором ток отстает от напряжения на четверть периода, конденсатор же, наоборот, заставляет напряжение в цепи отставать по фазе от тока на четверть периода. Таким образом, действие индуктивного сопротивления на сдвиг фаз между током и напряжением в цепи противоположно действию емкостного сопротивления.
Это приводит к тому, что общий сдвиг фаз между током и напряжением в цепи зависит от соотношения величин индуктивного и емкостного сопротивлений.
Если величина емкостного сопротивления цепи больше индуктивного, то цепь носит емкостный характер, т. е. напряжение отстает по фазе от тока. Если же, наоборот, индуктивное сопротивление цепи больше емкостного, то напряжение опережает ток, и, следовательно, цепь носит индуктивный характер.
Общее реактивное сопротивление Хобщ рассматриваемой нами цепи определяется путем сложения индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора ХС.
Но так как действие этих сопротивлений в цепи противоположно, то одному из них, а именно Хс приписывается знак минус, и общее реактивное сопротивление определяется по формуле:
Применив к этой цепи закон Ома, получим:
Формулу эту можно преобразовать следующим образом:
В полученном равенстве I XL — действующее значение слагающей общего напряжения цепи, идущей на преодоление индуктивного сопротивления цепи, а I ХС — действующее значение слагающей общего напряжения цепи, идущей на преодоление емкостного сопротивления.
Таким образом, общее напряжение цепи, состоящей из последовательного соединения катушки и конденсатора, можно рассматривать как состоящее из двух слагаемых, величины которых зависят от величин индуктивного и емкостного сопротивлений цепи.
Мы считали, что такая цепь не обладает активным сопротивлением. Однако в тех случаях, когда активное сопротивление цепи не настолько уже мало, чтобы им можно было пренебречь, общее сопротивление цепи определяется следующей формулой:
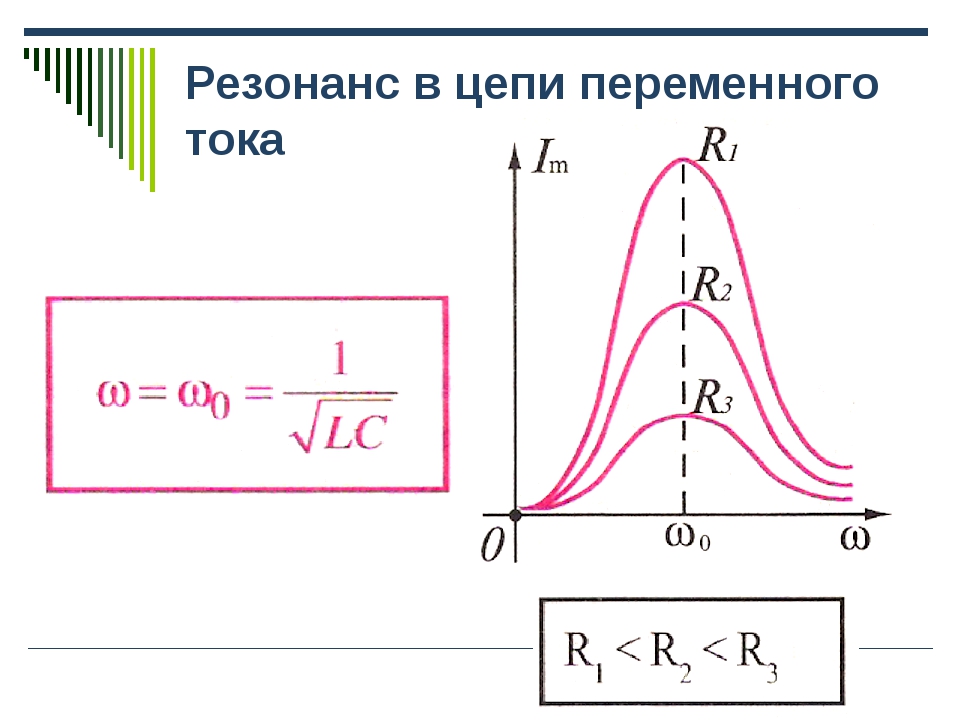
Резонанс напряжений в цепи переменного тока
Индуктивное и емкостное сопротивления, соединенные последовательно, вызывают в цепи переменного тока меньший сдвиг фаз между током и напряжением, чем если бы они были включены в цепь по отдельности.
Иначе говоря, от одновременного действия этих двух различных по своему характеру реактивных сопротивлений в цепи происходит компенсация (взаимное уничтожение) сдвига фаз.
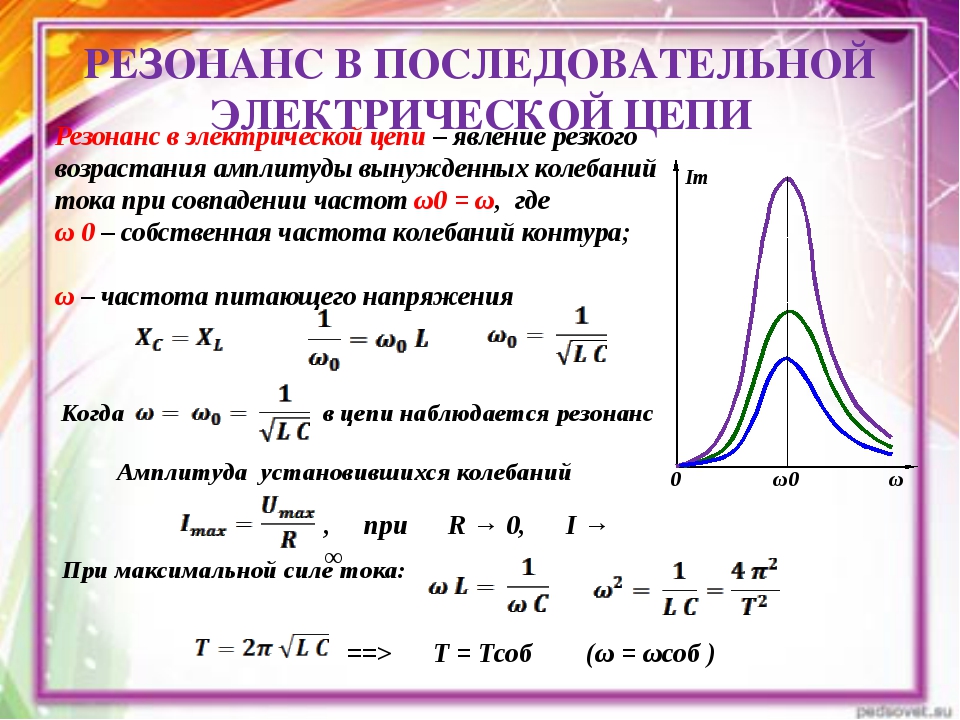
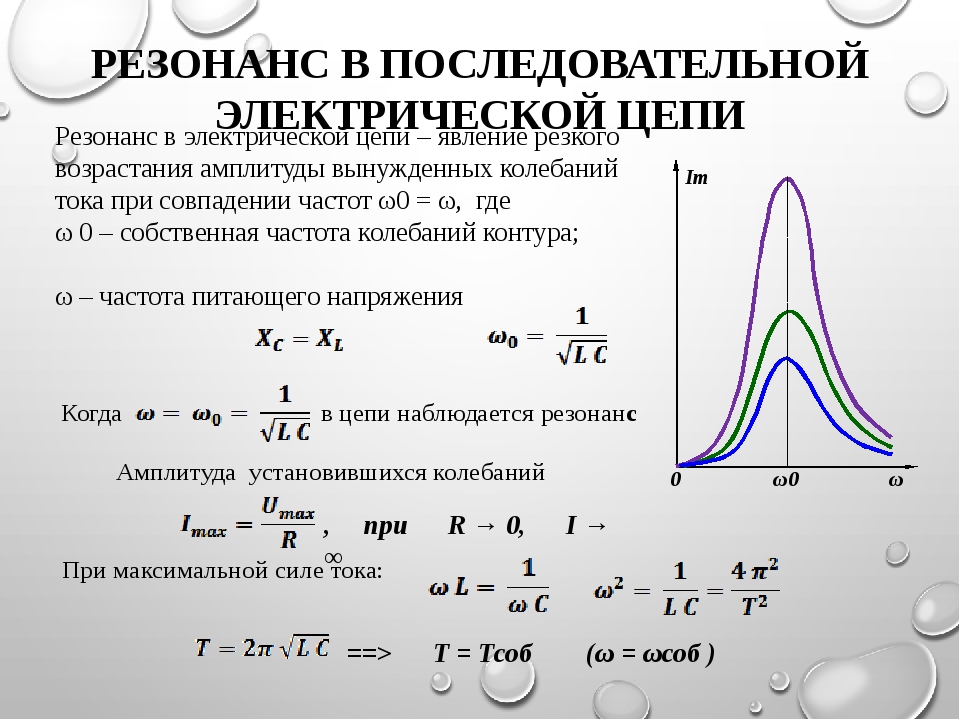
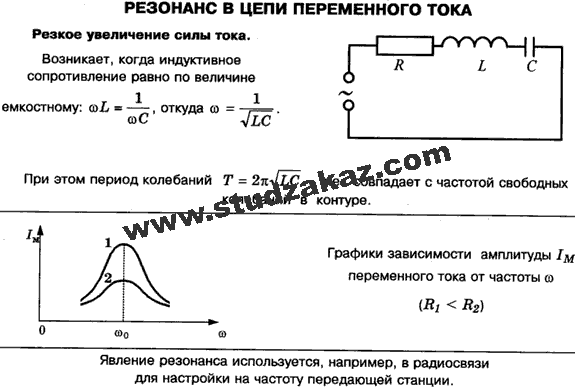
Полная компенсация, т. е. полное уничтожение сдвига фаз между током и напряжением в такой цепи, наступит тогда, когда индуктивное сопротивление окажется равным емкостному сопротивлению цепи, т. е. когда XL = ХС или, что то же, когда ω L = 1 / ωС.
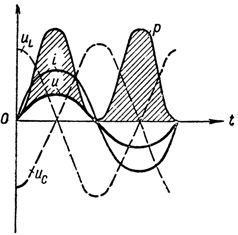
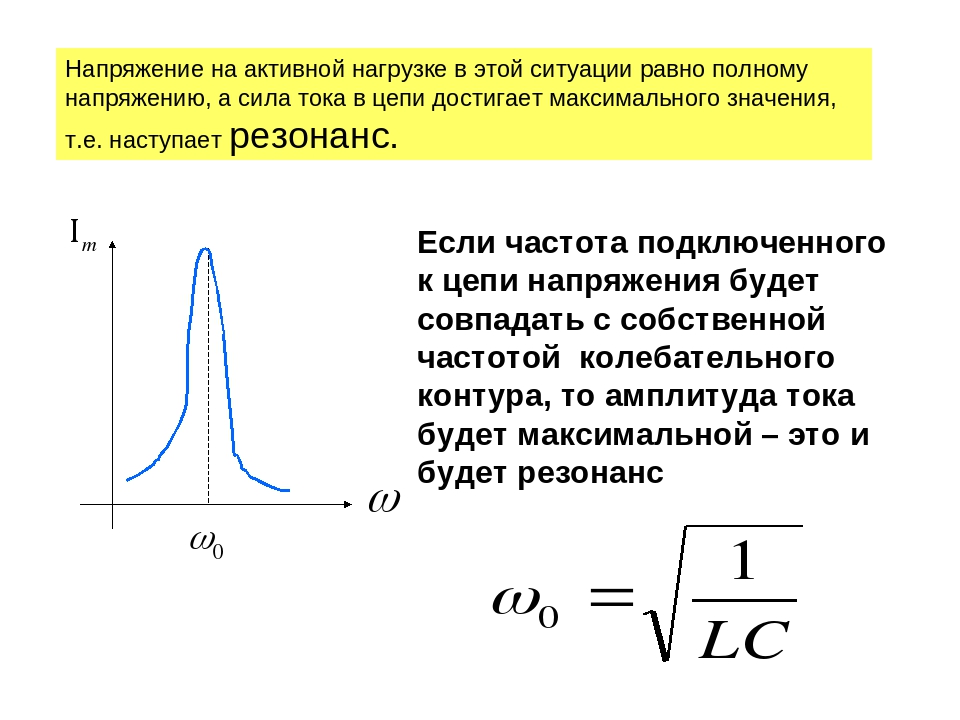
На рис. 1 приведены кривые напряжений, тока и мощности при резонансе напряжений в цепи.
График тока напряжений и мощности при резонансе напряжений
Следует твердо помнить, что сопротивления XL и ХС являются переменными, зависящими от частоты тока, и стоит хотя бы немного изменить частоту его, например, увеличить, как XL = ω L возрастет, а ХС = = 1 / ωС уменьшится, и тем самым в цепи сразу нарушится резонанс напряжений, при этом наряду с активным сопротивлением в цепи появится и реактивное. То же самое произойдет, если изменить величину индуктивности или емкости цепи.
При резонансе напряжений мощность источника тока будет затрачиваться только на преодоление активного сопротивления цепи, т. е. на нагрев проводников.
Действительно, в цепи с одной катушкой индуктивности происходит колебание энергии, т. е. периодический переход энергии из генератора в магнитное поле катушки. В цепи с конденсатором происходит то же самое, но за счет энергии электрического поля конденсатора. В цепи же с конденсатором и катушкой индуктивности при резонансе напряжений (XL = ХС) энергия, раз запасенная цепью, периодически переходит из катушки в конденсатор и обратно и на долю источника тока выпадает только расход энергии, необходимый для преодоления активного сопротивления цепи. Таким образом, обмен энергии происходит между конденсатором и катушкой почти без участия генератора.
Стоит только нарушить резонанс напряжений в цени, как энергия магнитного поля катушки станет не равной энергии электрического поля конденсатора, и в процессе обмена энергии между этими полями появится избыток энергии, который периодически будет то поступать из источника в цепь, то возвращаться ему обратно цепью.
Явление это очень сходно с тем, что происходит в часовом механизме. Маятник часов мог бы непрерывно колебаться и без помощи пружины (или груза в часах-ходиках), если бы не силы трения, тормозящие его движение.
Пружина же, сообщая маятнику в нужный момент часть своей энергии, помогает ему преодолеть силы трения, чем и достигается непрерывность колебаний.
Подобно этому и в электрической цепи, при явлении резонанса в ней, источник тока расходует свою энергию только на преодоление активного сопротивления цепи, тем самым поддерживая в ней колебательный процесс.
Из равенства XL = ХС можно определить значения частоты генератора, при которой наступает явление резонанса напряжений:
Значение емкости и индуктивности цепи, при которых наступает резонанс напряжений :
Таким образом, изменяя любую из этих трех величин ( f рез, L и С), можно вызвать в цепи резонанс напряжений, т. е. превратить цепь в колебательный контур.
Пример полезного применения резонанса напряжений : входной контур приемника настраивается конденсатором переменной емкости (или вариометром) таким образом, что в нем возникает резонанс напряжений. Этим достигается необходимое для нормальной работы приемника большое повышение напряжения на катушке по сравнению с напряжением в цепи, созданным антенной.
Наряду с полезным использованием явления резонанса напряжений в электротехнике технике часто бывают случаи, когда резонанс напряжений вреден. Большое повышение напряжения на отдельных участках цепи (на катушке или на конденсаторе) по сравнению с напряжением генератора может привести к порче отдельных деталей и измерительных приборов.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Что такое резонанс напряжений?
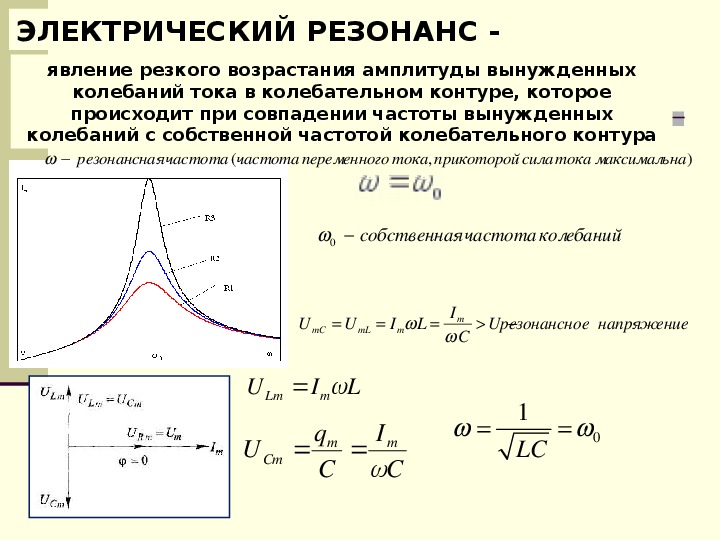
Резонансные явления наблюдаются в колебательных системах, когда частота собственных колебаний элементов системы совпадает с частотой внешних (вынужденных) колебательных процессов. Данное утверждение справедливо и для цепей с циркулирующим переменным током. В таких электрических цепях при наличии определённых условий возникает резонанс напряжений, что влияет на параметры тока. Явление резонанса в электротехнике может быть полезным или вредным, в зависимости от ситуации, в которой происходит процесс.
Описание явления
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.

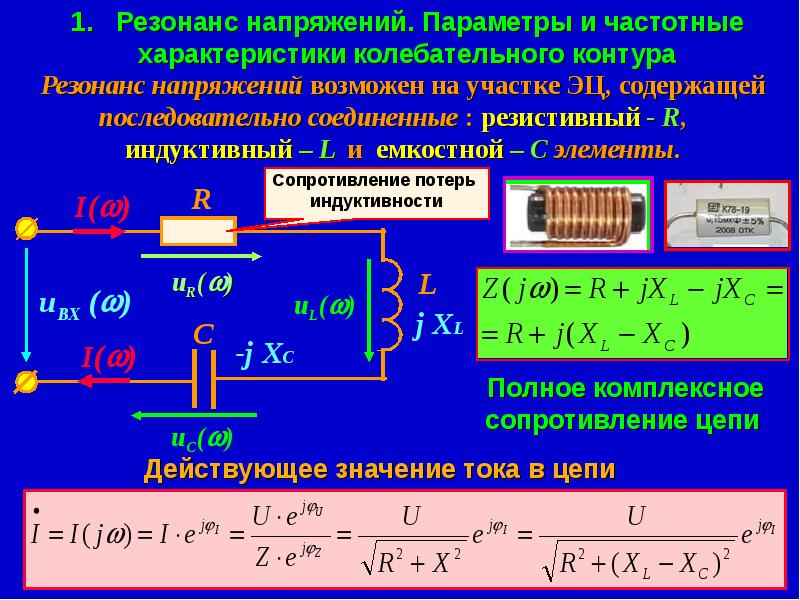
Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Формула
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в).

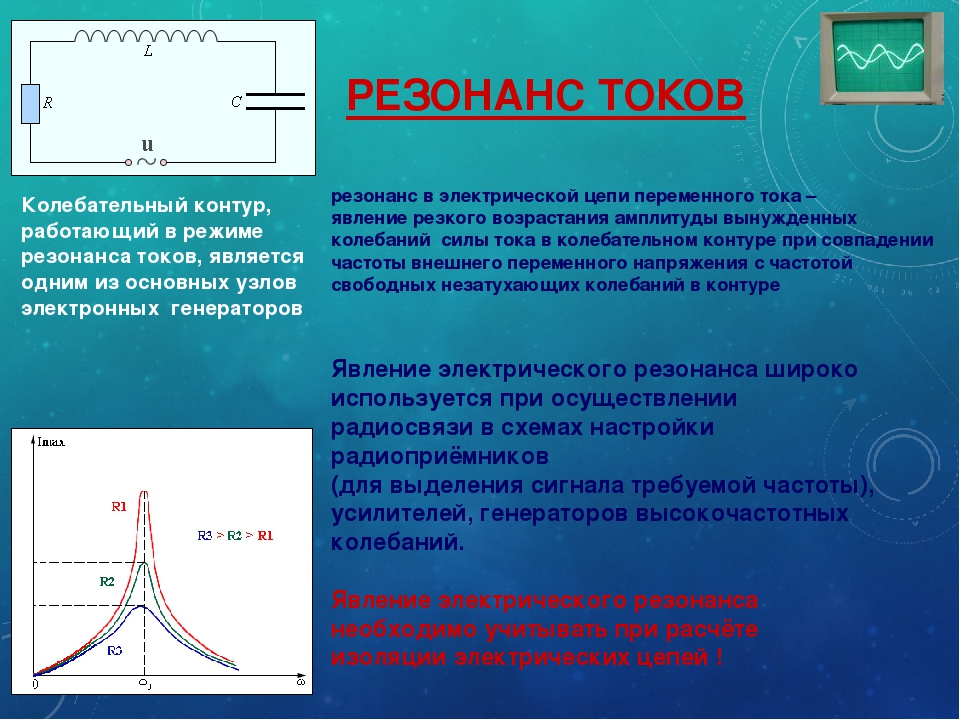
Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).


В режиме резонанса мощность источника питания будет рассеиваться только на активных сопротивлениях (в том числе на активном сопротивлении катушки). Для резонансных контуров характерны потери только активной мощности, которая израсходуется на поддержание колебательного процесса. Реактивная мощность на L C — элементах при этом не расходуется. Ток в резонансном режиме принимает максимальное значение:
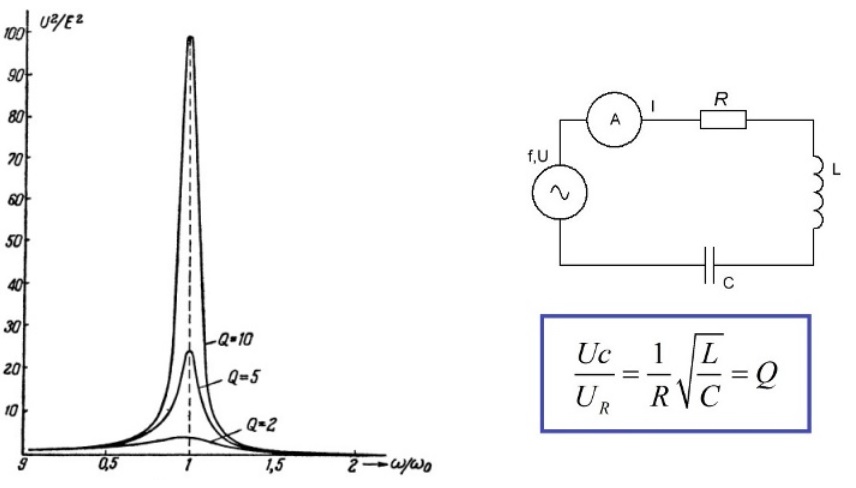
Величину Q принято называть термином «Добротность контура». Данный параметр показывает, во сколько раз напряжение, возникшее на контактах реактивных элементов, превышает входное напряжение U электрической сети. Для описания соотношения выходного и входного напряжений часто применяют коэффициент K. При резонансе:
Формулировка
На основании вышеописанных явлений, сформулируем определение резонансного напряжения: «Если общее падение напряжения на ёмкостно-индуктивных элементах равно нулю, а амплитуда тока – максимальна, то такое особое состояние системы называется резонансом напряжений». Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.
Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].
Если ω = ω0 – возникает резонанс напряжений. Частоты совпадают в том случае, когда индуктивное сопротивление сравняется с ёмкостным сопротивлением конденсатора. В таких случаях в цепи будет действовать только активное сопротивление R. Наличие реактивных элементов в схеме приводит к увеличению полного сопротивления цепи (Z):
где R – общее активное сопротивление.
Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.
Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.
Поскольку XL и Xc зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.
Условия наступления
Резонансные явления наступают только при наличии следующих условий:
При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.
Примеры применения на практике
Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.
Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.
Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.
Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.

Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.
Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.
Резонанс в электрической цепи
При каких условиях возникает явление: основные условия
Резонанс электротоков и напряжений появляется в результате сохранения тождества реактивных характеристик сопротивляемости сети. Несмотря на это, в ней должна быть и активная характеристика хотя бы минимального значения. Частота же генератора питания соединения всегда должна совпадать с частотой резонанса контура индуктивно-емкостной сети.
Обратите внимание! Условие работы сопротивления активного типа в реальных действующих схемах выполняется практически всегда. Одна лишь реактивная характеристика емкости и индуктивности возможна только в изолированных и теоретических примерах

Во время резонанса дроссель и конденсатор обмениваются накопленной энергией. В теоретических примерах, когда происходит первое подключение электрогенератора (в качестве питательного источника), энергия копится в катушке индуктивности или конденсаторе. После выключения электрогенератора из сети возникают колебания незатухающего характера, возникшие в результате этого обмена.
Добротность колебательной системы
Последовательный метод соединения функциональных компонентов можно использовать для рассмотрения других важных параметров колебательного контура. Напряжение на конденсаторе (Uс) при воздействии сигнала с частотой резонанса (Fрез) определяется волновым сопротивлением:
Такая же разница потенциалов будет образована на катушке индуктивности. Польза и вред рассматриваемого явления уточняются по добротности (Q = p/R = (1/R)/ √L/C) = (Fк*L)/R = 1/Fк*R*C) и затуханию (1/Q). Здесь Fк обозначает собственную частоту контура.
Добротность определяет эффективность системы. Вычисленная величина показывает отношение энергии, запасенной контуром, к потерям за один цикл колебаний. Этот параметр определяет избирательность приемников и передатчиков радиосигналов. Для оценки измеряют ширину спектра, при котором амплитуда сигнала уменьшается до 70% от максимального значения. Разницу частот (ΔF) называют полосой пропускания. Добротность можно выразить следующим образом:

Резонанс напряжений
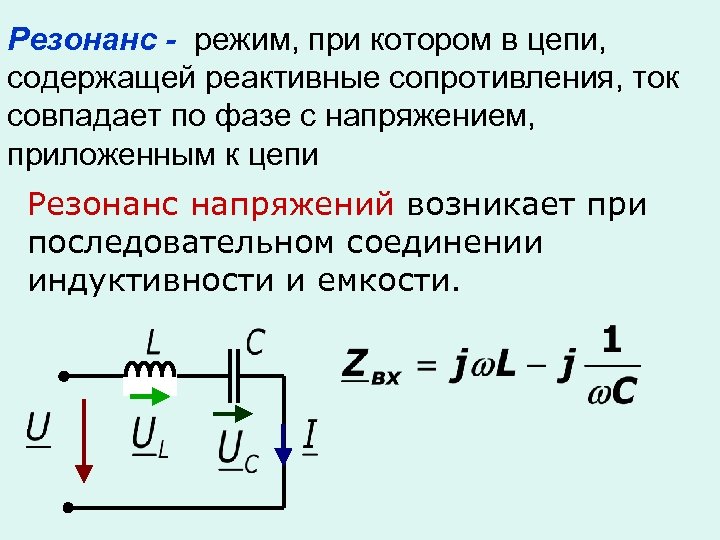
Если последовательно с генератором соединить конденсатор и катушку индуктивности, то, при условии равенства их реактивных сопротивлений, возникнет резонанс напряжений. При этом активная часть Z должно быть как можно меньшей.
Стоит отметить, что индуктивность и емкость обладает только реактивными качествами лишь в идеализированных примерах. В реальных же цепях и элементах всегда присутствует активное сопротивление проводников, хоть оно и крайне мало.
При резонансе происходит обмен энергией между дросселем и конденсатором. В идеальных примерах при первоначальном подключении источника энергии (генератора) энергия накапливается в конденсаторе (или дросселе) и после его отключения происходят незатухающие колебания за счет этого обмена.
Напряжения на индуктивности и емкости примерно одинаковы, согласно :
Где X — это Xc емкостное или XL индуктивное сопротивление соответственно.
Цепь, состоящую из индуктивности и емкости, называют колебательным контуром. Его частота вычисляется по формуле:
Период колебаний определяется по формуле Томпсона:
Так как реактивное сопротивление зависит от частоты, то сопротивление индуктивности с ростом частоты увеличивается, а у ёмкости падает. Когда сопротивления равны, то общее сопротивление сильно снижается, что отражено на графике:
Основными характеристиками контура являются добротность (Q) и частота. Если рассмотреть контур в качестве четырехполюсника, то его коэффициент передачи после несложных вычислений сводится к добротности:
А напряжение на выводах цепи увеличивается пропорционально коэффициенту передачи (добротности) контура.
При резонансе напряжений, чем выше добротность, тем больше напряжение на элементах контура будет превышать напряжение подключенного генератора. Напряжение может повышаться в десятки и сотни раз. Это отображено на графике:
Потери мощности в контуре обусловлены только наличием активного сопротивления. Энергия из источника питания берется только для поддержания колебаний.
Коэффициент мощности будет равен:
Эта формула показывает, что потери происходят за счет активной мощности:
Резонанс в распределённых колебательных системах, нелинейные процессы
Общим понятием для всех явлений данной категории можно назвать действенную связь с окружающей средой. В механических системах влияние на амплитуду фазовых характеристик процесса оказывает определенное положение в пространстве. В колебательном контуре радиоприемника, кроме собственного затухания, приходится учитывать реальный электромагнитный фон. При определенных условиях с высоким значением добротности допустимо образование стоячих волн.






Если пружина создана с различным распределением плотности витков, типовые формулы не действуют. Стандартные расчеты подразумевают равномерные упругость и деформации каждой части. Для уточнения нелинейности применяют корректирующие коэффициенты, сложные многоэтапные схемы вычислений.
Аналогичные особенности учитывают при использовании диодов или других радиотехнических компонентов с переменными амплитудно-частотными характеристиками. Если катушку индуктивности намотать на сердечнике из ферромагнитного материала, также придется учитывать нелинейность выходных параметров. Ее не получится описать элементарным уравнением закона Ома.
В нелинейных контурах при определенном спектральном распределении внешних воздействий присутствуют гармонические колебания. Кроме совпадения частот, значение имеет их амплитуда. В зависимости от настроек, они способны выполнять полезные и вредные функции. Определенные условия вызывают искажение формы базового сигнала.
Какие последствия резонанса напряжений
Если в электрической системе с ёмкостью, индуктивностью и сопротивлением не учитывать воздействие этого явления, то работа устройств может быть нестабильной. Если этот эффект носит паразитический характер, то от него следует обязательно избавляться. Увеличение напряжения вследствие возникновения резонансного явления в цепи переменного напряжения может привести к выходу элементов из строя.
Важно! При возникновении этого явления могут быть разрушены конденсаторы из-за превышения реактивной мощности. При перегреве вследствие резонанса напряжений электротехника может не только выйти из строя, но и загореться
При перегреве вследствие резонанса напряжений электротехника может не только выйти из строя, но и загореться.

На крупных производственных объектах такое явление может привести к аварии с человеческими жертвами. Если высоковольтные линии электропередач находятся слишком близко, то эффект электрического резонанса может возникать и в системах этого типа.

Чтобы защитить ЛЭП от негативного воздействия этого явления применяются шунтирующие генераторы, которые устанавливаются через каждые 300 – 400 км.
Что такое резонансное напряжение
Если в сеть с переменным электротоком последовательно подключены дроссель и конденсаторный элемент, они способны по-своему воздействовать на генератор, который питает всю схему. Также они влияют на фазовые отношения тока и напряженности. Индуктивная катушка привносит в цепь сдвиг фаз, который заставляет электроток отставать от напряжения на четверть периода. Конденсирующий элемент, наоборот, работает так, что U отстает от тока на четверть по фазе.

Это означает, что сопротивляемость индуктивного типа, которое работает на сдвижение фазы напряжения и тока в сети, функционирует противоположно силе емкостного сопротивления.

К сведению! Данный процесс приводит к тому, что общий сдвиг по фазе между силой тока и напряженностью в сети всегда зависит от отношения величины индуктивной и емкостной сопротивляемостей.

Если емкостное R в сети больше индуктивного, то все соединение является емкостным. Это значит, что напряжение характеризуется разностью фаз по току. Иногда бывает и обратная ситуация, индуктивное сопротивление сети получается большим, чем емкостное. В этом случае вся сеть становится индуктивной.
Достижение размытия резонанса
Для частичного уменьшения или размытия (смягчения) резонанса необходимо выполнить одно из условий снижения амплитуды. Эффект амортизации заключается в том, чтобы:
Существует множество приспособлений и конструктивных решений, позволяющих это сделать. К наиболее удачным относятся:
Один из универсальных методов, предназначенных для размытия резонанса, предлагает использовать два связанных элемента. У элементов изменения жесткости происходят по двум разным законам: линейному и нелинейному. Вместе соединяются витая пружина и прессованная проволока, представляющая собой демпфирующий компонент упругого действия.
Задача из ЕГЭ по физике про резонанс в цепи переменного тока
При подключении трех неизвестных элементов A, B и C электрической цепи к выходу генератора переменного тока с изменяемой частотой гармонических колебаний при неизменной амплитуде колебаний напряжения, обнаружены следующие зависимости действующих значений силы тока от частоты:
Установите соответствие между буквой графика и соответствующим элементом из списка, который был подключен:
1) активное сопротивление
2) конденсатор
3) катушка
4) RLC-контур
Механические колебания маятника
Самая простая модель, которая может наглядно показать колебания, это простейший маятник, а точнее математический маятник. Колебания разделяют на свободные и вынужденные. Первоначально воздействующая энергия на маятник обеспечивает в теле свободные колебания без присутствия внешнего источника переменной энергии воздействия. Данная энергия может быть как кинетической, так и потенциальной.
Здесь не имеет значение насколько сильно или нет качается сам маятник, — время, потраченное на прохождения его пути в прямом и обратном направлении, сохраняется неизменным. Во избежание недоразумений с затуханием колебаний вследствие трения о воздух стоит выделить, что для свободных колебаний должны соблюдаться условия возврата маятника в точку равновесия и отсутствия трения.
А вот частота в свою очередь напрямую зависит от величины длины нити маятника. Чем короче нить, тем выше частота и наоборот.
Возникающая естественная частота тела под воздействием первоначально приложенной силы называется резонансной частотой.
Все тела, которым свойственны колебания, совершают их с заданной частотой. Для поддержания в теле незатухающих колебаний необходимо обеспечить постоянную периодическую энергетическую «подпитку». Это достигается воздействием в одновременный такт колебаний тела постоянной силы с определенным периодом. Таким образом возникающие колебания в теле под действием периодической силы снаружи называют вынужденными.
В какой-то момент внешних воздействий возникает резкий скачок амплитуды. Такой эффект возникает если периоды внутренних колебаний тела совпадают с периодами внешней силы и называется резонансом. Для возникновения резонанса достаточно совсем небольших величин внешних источников воздействия, но с обязательным условием повторения в такт. Естественно, при фактических расчетах в земных условиях не стоит забывать о действии сил трения и сопротивления воздуха на поверхность тело.




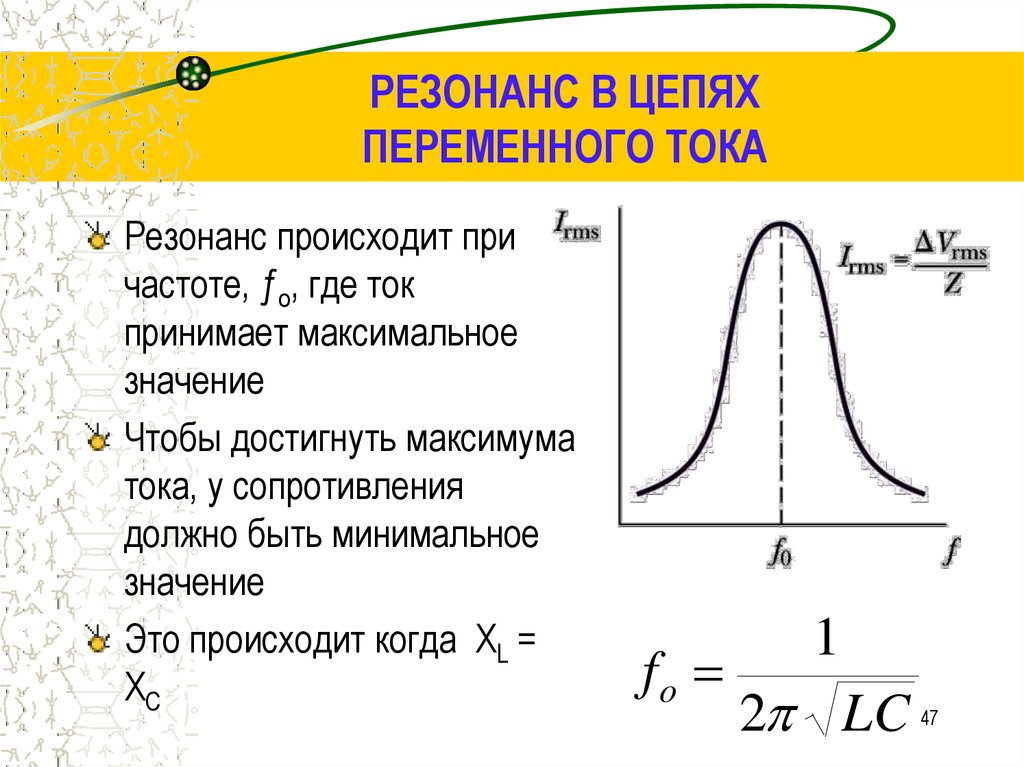
Явление резонанса в цепи переменного тока
Напомним, что частота переменного тока связана с циклической частотой переменного тока простым соотношением:
Векторная диаграмма для случая резонанса в цепи переменного тока, состоящей из катушки, конденсатора и активного сопротивления, соединенных последовательно, имеет вид:
Реактивные сопротивления индуктивности и емкости
Индуктивностью называется способность тела накапливать энергию в магнитном поле. Для нее характерно отставание тока от напряжения по фазе. Характерные индуктивные элементы — дросселя, катушки, трансформаторы, электродвигатели.
Емкостью называются элементы, которые накапливают энергию с помощью электрического поля. Для емкостных элементов характерно отставание по фазе напряжения от тока. Емкостные элементы: конденсаторы, варикапы.
Приведены их основные свойства, нюансы в пределах этой статьи во внимание не берутся. Кроме перечисленных элементов другие также имеют определенную индуктивность и емкость, например в электрических кабелях распределенные по его длине
Кроме перечисленных элементов другие также имеют определенную индуктивность и емкость, например в электрических кабелях распределенные по его длине.
Резонанс в электрических цепях как явление
Общее определение резонанса вполне приемлемо для рассмотрения аналогичных электрических процессов. Природа явления в данном случае зависит от параметров компонентов, формирующих цепь прохождения сигнала. Индукционный элемент и конденсатор выполняют функции накопителей энергии. Постепенное уменьшение амплитуды обеспечивает электрическое сопротивление – аналог силы трения в механической системе.
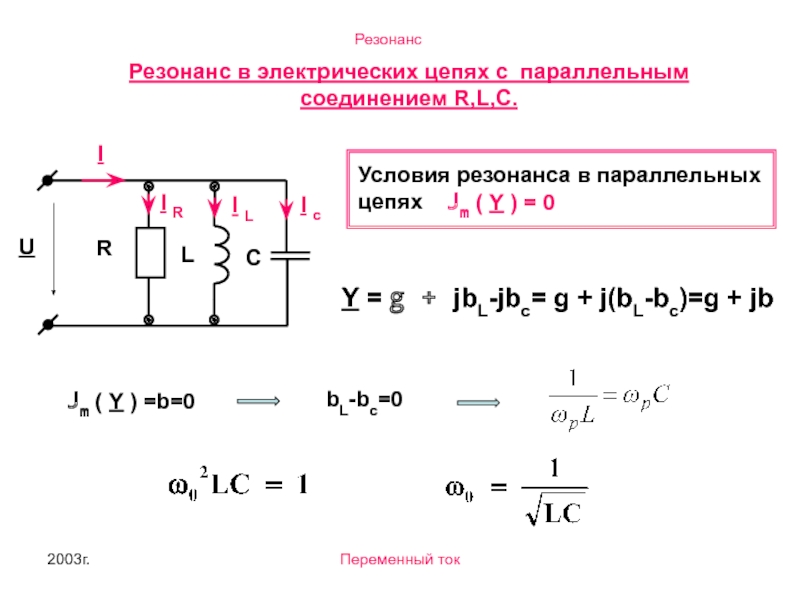
Различают параллельный и последовательный резонанс при выборе соответствующего схемотехнического решения. В первом варианте обеспечивают увеличение силы тока при совпадении частот. Во втором – напряжения.
Определить значение рабочих параметров контура можно после вычисления полного сопротивления (Z). При последовательном соединении типовой цепочки (R, L и C) применяют следующую формулу:
Z = √ R2 + (2π * f * L – 1/2π * f * C)2.
По закону Ома несложно определить ток:
I = U/Z = U/ √ R2 + (2π * f * L – 1/2π * f * C)2.

Что такое резонанс напряжений, показано на рисунке.
Собственная частота резонансного контура
Мы можем заставить систему колебаться с собственной частотой. Для этого сначала необходимо зарядить конденсатор, как показано на верхнем рисунке слева. Когда это будет выполнено, ключ переводится в положение, показанное на том же рисунке справа.
В момент времени «0» вся электрическая энергия сохраняется в конденсаторе, и ток в контуре равен нулю (рисунок внизу)
Обратите внимание, что верхняя пластина конденсатора заряжена положительно, а нижняя — отрицательно. Мы не можем видеть колебания электронов в цепи, но мы можем измерить ток амперметром, а при помощи осциллоскопа отследить характер зависимости тока от времени
Отметим, что T на нашем графике — это время, необходимое для завершения одного колебания, носящего в электротехнике название «период колебания».
Ток течет по часовой стрелке (рисунок внизу). Энергия передается из конденсатора в катушку индуктивности. На первый взгляд может показаться странным, что индуктивность содержит энергию, однако это похоже на кинетическую энергию, содержащуюся в движущейся массе.
Поток энергии возвращается обратно в конденсатор, но обратите внимание, что полярность конденсатора теперь изменилась. Другими словами, нижняя пластина теперь имеет положительный заряд, а верхняя пластина — отрицательный заряд (рисунок внизу)
Теперь система полностью обратилась, и энергия начинает поступать из конденсатора опять в индуктивность (рисунок внизу). В итоге энергия полностью возвращается к своей отправной точке и готова начать цикл заново.




Частота колебаний может быть аппроксимирована следующим образом:
где: F — частота, L — индуктивность, C — емкость.
Рассмотренный на этом примере процесс отражает физическую суть резонанса напряжений.
Добротность колебательной системы
Ещё одной из характеристик колебательной системы (КС) является добротность. Она обозначается буквой Q и находится по общей формуле:
Добротность определяет отношение запаса энергии в КС к потерям за интервал фазных изменений на величину в 1 радиан. Она показывает ширину резонансной полосы.
Внимание! Формула для вычисления Q говорит о том, что в каждом периоде скорость затухания колебаний и количество потерянной энергии тем меньше, чем выше значение добротности КС. Добротность колебательной системы

Польза и вред резонансов
Полезный результат понятен из примера с колоколом. Человек со средними физическими способностями способен создать перезвон, который слышен на очень большом расстоянии. Для аналогичной силы звука с применением электронной аппаратуры необходимо применить мощнейший усилитель и огромный динамик.

Резкий нерегулируемый рост амплитуды на определенном уровне превышает прочностные характеристики конструкции. Именно такое воздействие ветровых нагрузок разрушило такомский мост в США. Чтобы исключить опасные ситуации, вместо сложного инженерного расчета офицеры командуют солдатам шагать не в ногу при переходе водных преград по таким конструкциям.
Применение резонансного явления
Резонанс в электрических цепях используют для фильтрации сигналов. Выбирают соответствующую схему обработки для ограничения необходимого диапазона либо расширения полосы пропускания.
С помощью последовательного контура можно повысить напряжение питания, если снабжающая организация не обеспечивает стабильность параметров сети. Такие неприятности встречаются при подключении потребителей на дачных участках и в коттеджных поселках, в сравнительно небольших населенных пунктах.
Недостаток ликвидируют конденсаторами, которые добавляют в электрическую цепь. Подобные решения помогают восстановить работоспособность дрели, станка, другого мощного оборудования. Обмотки соответствующего привода выполняют функции индуктивного компонента колебательного контура.
Параллельное подключение конденсаторов компенсирует потери, созданные реактивной мощностью. Этот вариант обеспечивает циркуляцию энергии между накопителем и подключенной обмоткой. Без такого дополнения часть энергии будет бесполезно потребляться сетью питания. Следует подчеркнуть, что счетчик в любом случае фиксирует потребление. Данная модернизация поможет сэкономить на оплате коммунальных услуг.
Резонансные явления способны чрезмерно увеличить силу тока или напряжение. Необходим точный расчет электрических цепей, чтобы предотвратить перегрев и повреждение проводов, короткие замыкания и другие аварийные ситуации.
Амплитуда резонанса
В КК при подаче переменного напряжения от внешнего источника наблюдаются два вида резонанса и резкое увеличение двух видов амплитуды: амплитуды тока и амплитуды напряжения.
Амплитуда тока
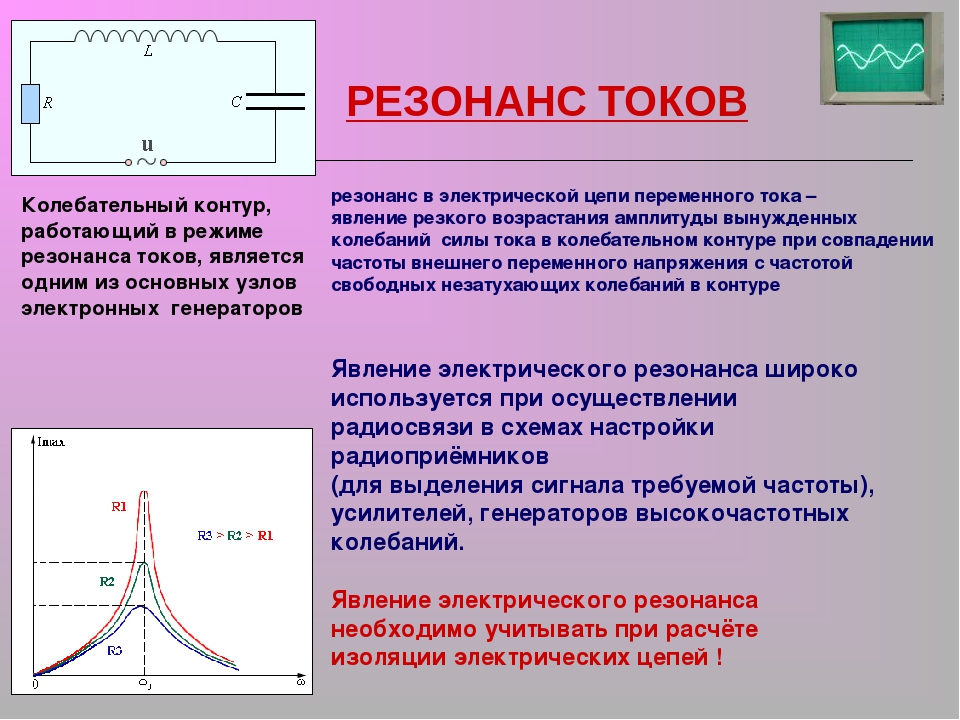
Амплитуда тока резко возрастает при резонансе напряжений в последовательном контуре (последовательный резонанс). Источник переменной ЭДС включён в цепь, где нагрузкой служат последовательно включённые элементы L и С.
В этом случае в цепь входят сопротивления: активное r и реактивное x, равное:
Так как для внутренних колебаний xL и xC равны, то для тока, поступающего от генератора, при резонансе (когда частоты совпадают) эти значения тоже одинаковы. Поэтому x = 0. В итоге полное сопротивление цепи будет состоять только из небольшого активного сопротивления. Ток при этом получается максимальным.

Амплитуда напряжения
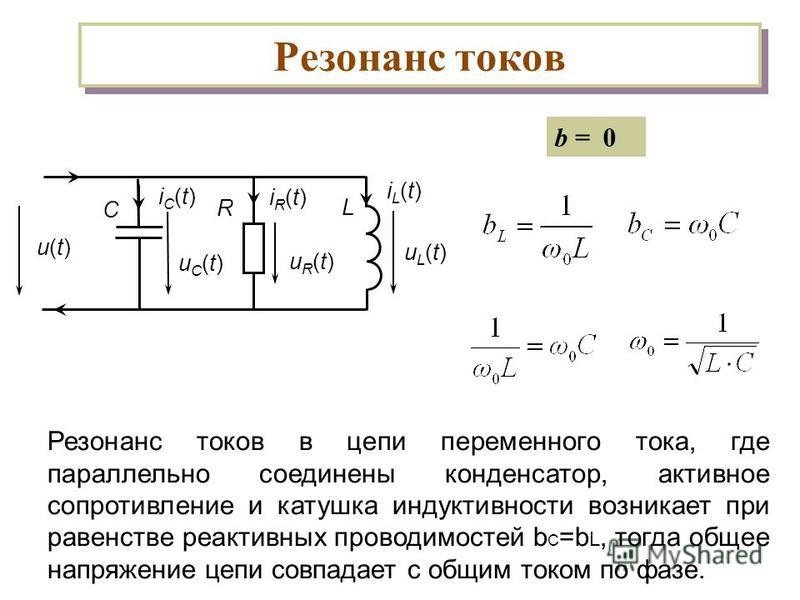
Резонанс токов (параллельный резонанс) является условием резкого возрастания амплитуды напряжения. Источник ЭДС подключается вне контура и нагружен параллельно соединёнными элементами L и С. В этом случае на эффект резонанса влияет внутреннее сопротивление генератора. Амплитуда напряжения на контуре максимальна при малом отличии напряжения контура от напряжения генератора. Это возможно при малом Ri.
Внимание! Изменение частоты генератора меняет ток, а амплитуда напряжения на контуре не отстаёт по величине от напряжения на генераторе. Если, U = Е – I*Ri, где Е – ЭДС, I – ток, то при малом Ri U = Е

Формула для определения расчётной резонансной частоты для разных колебательных систем различается по входящим в неё параметрам. Несмотря на все различия, суть остаётся неизменной: эффект резонанса наступает тогда, когда частота внутренних колебаний системы и внешних воздействий становятся равны друг другу.




Положительные и отрицательные стороны резонанса
Увеличение колебаний в два раза и более, по сравнению с исходным допуском технического задания, способно привести к разрушению конструкции. Однако это же проявление в другой ситуации выполняет полезные функции. Плюсы и минусы резонанса удобно изучать на конкретных примерах.

Для преобразования импульсного сигнала в синусоидальный можно применить представленный на рисунках инвертор. Принцип работы заключается в периодическом накоплении-возврате энергии с применением реактивных компонентов. При корректном выборе элементов колебательный контур выполняет функции фильтра. Трансформатор – это дополнительная индуктивность в цепи, поэтому основную катушку можно сделать меньше. Количеством витков обмоток устанавливают необходимое напряжение на выходе.
Определенный резон имеет создание системы отопления с помощью электроэнергии, созданной солнечными батареями. Эти «бесплатные» генераторы по мере совершенствования производственных технологий становятся дешевле. Эффективный индукционный нагреватель можно собрать самостоятельно. Некоторые схемы по КПД не уступают фабричным аналогам.

Следующие примеры резонанса демонстрируют отрицательные стороны явления:
Колебания и частота
Процедура, связанная с изменением положения системы рядом с точкой равновесного состояния и повторяющаяся с течением времени, называется колебаниями. Качающийся маятник повторяет свои движения относительно нормали к горизонтальной плоскости. При этом, если не прикладывать к его движению дополнительной энергии, его раскачивания затухнут.
Явление таких изменений можно классифицировать по следующим параметрам:
Внимание! Все колебания, независимо от своих физических свойств, имеют общие законы, которые можно описать волновыми явлениями. Эти закономерности исследует теория волновых колебаний
Механические колебания связаны с трансформацией одной формы энергии в другую, волновые – с пространственным передвижением и распространением энергии.
Общими параметрами для всех колебаний являются:
Частотой считают количество колебаний, совершаемых телом за единицу времени. Единица измерения – герц (Гц), графическое обозначение – f, ʋ. Частота может быть круговой – при периодичном движении точки по окружности, ещё её называют циклической:
Период (T) являет собой время целого (полного) колебания, во время которого можно зафиксировать повторение любой из характеристик состояния системы. Это значит, что она совершила полное колебание. Обозначение периода – Т, единица измерения – секунда (с).
Две величины T и f являются обратными, что следует из формул:
Наибольшее отклонение точки тела или любой величины системы от равновесного положения называется амплитудой колебаний и обозначается буквой A. Единицей измерения являются те величины, изменения которых рассматриваются. При механических отклонениях амплитуду измеряют в метрах (м), амплитуду переменного напряжения – в вольтах (В) и так далее.

Как правильно рассчитать резонансный контур
Колебательный контур — это цепь, которая характеризуется появлением в ней колебаний определенной частоты, зависящих от параметров этой цепи. Самый простой контур включает в себя последовательно или параллельно соединенные дроссель и конденсатор. Для расчета ƒ резонанса в контуре используют формулу ƒ = 1/(2π √LC), где L — индуктивность, а C — емкость.

Таким образом, было рассмотрено, при каких условиях возникает явление резонанса напряжений и что это такое. Наблюдается оно только в схемах, которые характеризуются емкостью и индуктивностью, где активное R крайне мало.
Кривые напряжения и тока в емкостном сопротивлении
В идеальной емкости ток опережает напряжение на 90°
Режим — состояние электрической цепи переменного тока описывается дифференциальными уравнениями, представляющими собой уравнения с постоянными коэффициентами и правой частью, например:
Из курса высшей математики известно, что общее решение такого уравнения может быть найдено методом наложения принужденного и свободного режимов:
— ток принужденного режима при di/dt=0
— ток свободного режима.
Свободные процессы исследуются с целью определения устойчивости системы. В устойчивой системе процессы должны затухать. Принужденный и свободный режимы в сумме определяют процессы, которые называются переходными, т.е. осуществляется переход от одного установившегося режима к другому.







При установившемся режиме ток и напряжение сохраняют в течение длительного времени амплитудные значения.
В цепях постоянного тока токи и напряжения остаются неизменными, а в цепях переменного тока остаются неизменными кривые изменения токов и напряжений.
Принцип действия резонансов токов
Если необходимо намеренно создать это явление, то достаточно подключить параллельно сопротивление, индуктивность и ёмкость. Для генерации этого явления следует подавать по проводникам только переменное напряжение. Если номиналы элементов были правильно рассчитаны, то в неразветвлённой части цепи образуется ток, который будет полностью совпадать по фазе и напряжению.

Частным примером генератора резонанса является колебательный контур радиоприёмника. В таких устройствах, с помощью поворотного механизма, изменяется ёмкость, что и вызывает настройку устройства приёма сигнала на определенную частоту.
Важно! Передающие радиостанции, как правило, всегда настроены на одну какую-либо частоту несущей волны
Параллельный резонанс при источнике ЭДС
Добротность для параллельной схемы вычисляют по формуле Q=R√C/L. При равенстве частот (источника и контура) сопротивление в отдельных ветвях не различается. Одинаковые значения токов создают компенсированные реактивные параметры конденсатора и катушки.
При отклонении частоты от резонансного значения в нижний (верхний) диапазон сопротивление приобретает емкостной (индуктивный) характер, соответственно. В обычном рабочем цикле происходит энергетический обмен между реактивными элементами цепи. Этот режим характеризуется увеличением в Q раз тока, проходящего по внутреннему контуру, по сравнению с поступающим от источника ЭДС. Идеальные условия, когда добротность стремится к бесконечной величине, невозможны. Прямые и паразитные потери в цепях ограничивают рост силы резонансного тока.
Резонанс в линейных колебательных системах с несколькими степенями свободы
Такие расчеты понадобятся при конструировании двух последовательных контуров с индуктивной связью. В этом случае переменные колебательные процессы оказывают взаимное влияние. Фактически речь идет о распределенной системе.
Кроме схемотехники, в подобных ситуациях отдельно изучают коэффициент связи (Кс). При работе с трансформатором его вычисляют делением напряжений на первичной (вторичной) катушке, соответственно. Следует учесть реактивные характеристики, которые преобладают в рабочем диапазоне частот.
Узнав, что такое резонанс напряжений и токов, можно самостоятельно реализовать различные проекты. Тщательная предварительная подготовка необходима для создания схемы с хорошими эксплуатационными параметрами. Начинают с чертежей и расчетной части. Теоретические изыскания дополняют изготовлением макета и практическими испытаниями. Ускоряют подготовку конструкторской документации, а также выполняют эксперименты с применением программного обеспечения. В наиболее сложных ситуациях обращаются к опытным специалистам.
Заключение
Резонанс напряжений и токов — интересное явление, о котором нужно знать. Он наблюдается только в индуктивно-емкостных цепях. В цепях с большим активным сопротивлениям он не может возникнуть. Подведем итоги, кратко ответив на основные вопросы по этой теме:
В индуктивно-емкостных цепях.
Возникает при условии равенства реактивных сопротивлений. В цепи должно быть минимальное активное сопротивление, а частота источника питания совпадать с резонансной частотой контура.
В обоих случаях по формуле: w=(1/LC)^(1/2)
Увеличив активное сопротивление в цепи или изменив частоту.
Теперь вы знаете, что такое резонанс токов и напряжений, каковы условия его возникновения и варианты применения на практике. Для закрепления материала рекомендуем просмотреть полезное видео по теме: