в чем измеряется реакция опоры

Сила реакции опоры

Сила реакции опоры — это сила, с которой опора действует на тело. Она направлена перпендикулярно поверхности, поэтому такую силу называют силой нормальной реакции. Обозначают ее символом N и измеряют в Ньютонах.

Тело находится на выпуклой или вогнутой поверхности

Рассмотрим рисунок 1. Тело находится на опоре и давит на нее своим весом. Опора реагирует на воздействие тела и отвечает ему силой \(\vec\). Эта сила направлена перпендикулярно поверхности, вдоль вектора нормали, поэтому ее называют нормальной силой.

Примечания:

\(\vec \left( H \right) \) – сила, с которой опора действует на тело.

Когда тело находится на выпуклой поверхности (рис. 1а), реакция направлена вдоль радиуса от центра сферы наружу, за ее пределы.

Если же тело находится на вогнутой части (рис. 1б) поверхности, реакция \(\vec\) направлена по радиусу внутрь сферической поверхности к ее центру.

Тело опирается на поверхность в двух точках

На рисунках 2а и 2б изображено продолговатое тело (к примеру, стержень), опирающееся на поверхности двумя своими точками.

В точках соприкосновения поверхность отвечает телу силой \(\vec\) своей реакции. Видно, что в каждая сила реакции направлена перпендикулярно поверхности.

Cилы реакции \(\vec>\) и \(\vec>\) имеют различные направления и в общем случае не равны по модулю.

Примечание: Сила — это вектор. Между векторами можно ставить знак равенства, только, когда совпадают характеристики векторов.

Как рассчитать силу нормальной реакции

Пусть тело давит на опору своим весом. В местах соприкосновения тела с опорой наблюдается упругая деформация. При этом опора стремится избавиться от возникшей деформации и вернуться в первоначальное состояние. Силы, с которыми опора упруго сопротивляется воздействию тела, имеют электромагнитную природу. Когда сближаются электронные оболочки атомов тела и опоры, между ними возникает сила отталкивания. Она и является силой реакции опоры на воздействие тела.

Примечание: Сила реакции \(\vec\) распределяется по всей площади соприкосновения тела и опоры. Но для удобства ее обычно считают сосредоточенной силой. Ее изображают на границах соприкасающихся поверхностей исходящей из точки, расположенной под центром масс тела.

Для того, чтобы рассчитать силу реакции, нужно понимать законы Ньютона, уметь составлять силовые уравнения и знать, что такое равнодействующая.

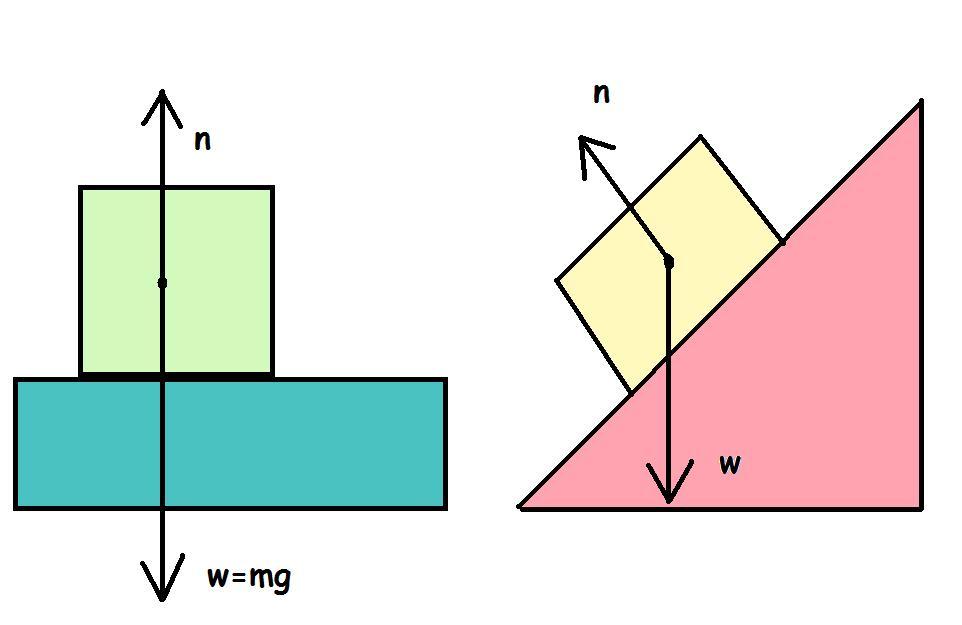
На рисунке 3 изображены тела, находящиеся на горизонтальной – а) и наклонной – б) поверхностях.

Рассмотрим подробнее рисунок 3а. Тело на горизонтальной поверхности находится в покое. Значит, выполняются условия равновесия тела.

По третьему закону Ньютона, сила, с которой тело действует на опору, равна по модулю весу тела и направлена противоположно весу.

\(m \vec \left( H \right) \) – сила, с которой тело действует на опору;

\(\vec \left( H \right) \) – сила, с которой опора отвечает телу;

Рисунок 3б иллюстрирует тело на наклонной поверхности. Перпендикулярно соприкасающимся поверхностям проведена ось Oy. Проекция силы \(m \vec\) на ось — это \(mg_\), она будет направлена противоположно реакции опоры \(\vec\) и численно равна ей.

Примечание: Выражение «численно равна» нужно понимать, как «длины векторов равны».

\(\alpha \left(\text <рад>\right) \) – угол между силой \(mg\) и осью Oy.

Источник

Некоторые физические явления сложны для понимания школьников. К таковым относится и сила реакция опоры. Скорее всего причина тут кроется в том, что этот тип взаимодействия между физическими предметами и телами противоречит житейской логике.

Между тем, достаточно немного усидчивости и терпения, чтобы убедиться, что это совсем не так.

Что такое сила реакции опоры

Прежде всего дадим определение данной силе. Сила реакции опоры (N) представляет собой взаимодействие на молекулярном уровне.

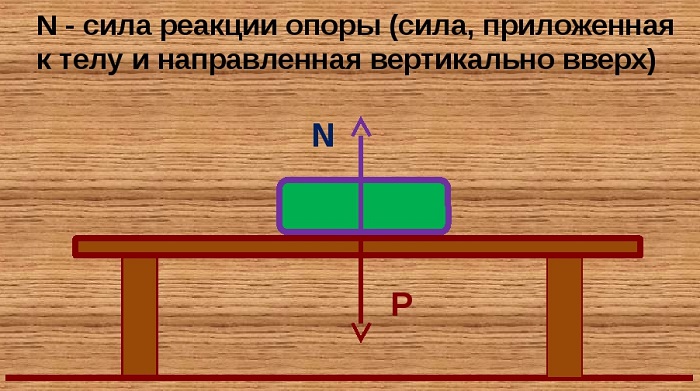
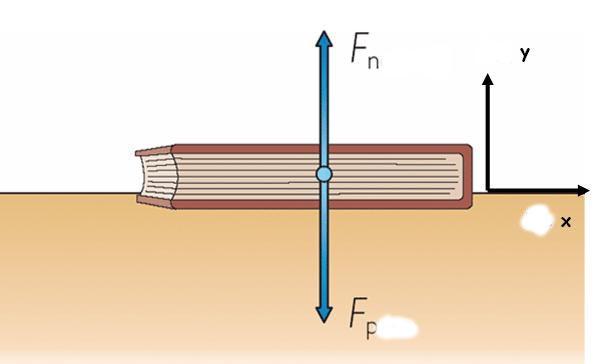
Это сила, приложенная к телу и направленная вертикально вверх.

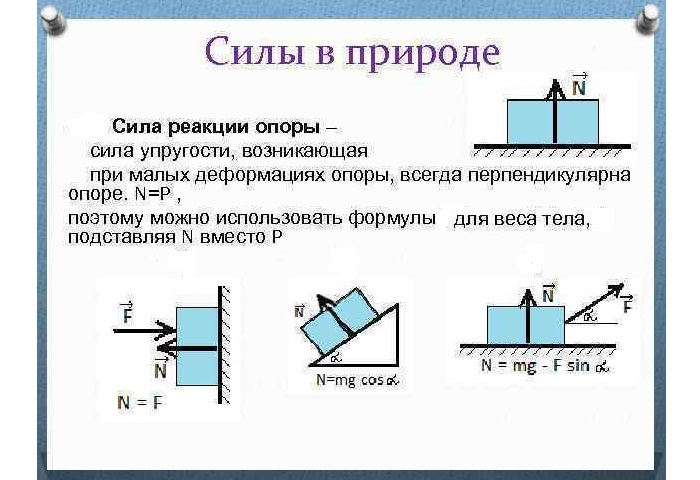
Сила реакции опоры — сила упругости, возникающая при малых деформациях опоры, всегда перпендикулярна опоре, N = P.

Книга, положенная на стол, давит на ее поверхность с определенной нагрузкой, но молекулы, сжатые ею, хотят снова прийти в равновесие и поэтому давят на книгу ровно с такой же силой. Если бы в природе не существовало этого взаимодействия, то тела не выдерживали бы нагрузки. Из этого можно заключить, что сила реакции опоры представляет собой разновидность силы упругости.

Примеры решения задач

Задача 1

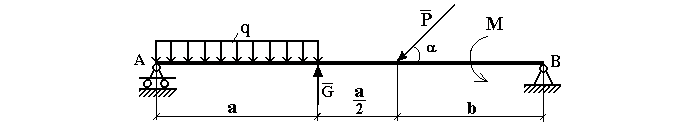
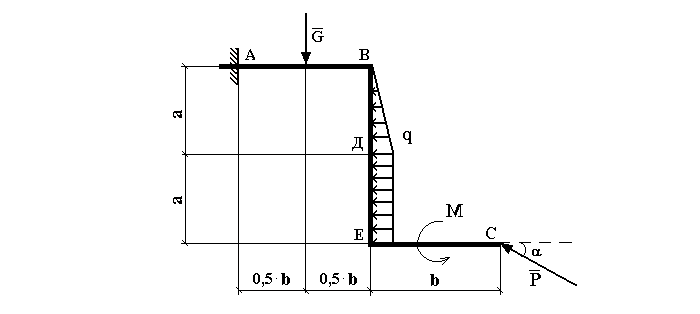
Определить реакции опор горизонтальной балки от заданной нагрузки.

Перед тем, как начать составлять систему уравнений, необходимо несколько преобразовать систему балки:

Опора А покоится на подвижной опоре, которая может двигаться в горизонтальной плоскости, поэтому имеет только вертикальную составляющую реакции опоры – R_A.

Опора В абсолютно неподвижна, и ее реакция опоры состоит из двух взаимодействий, направленных вдоль линий оси: X_B и Y_B.

Распределенную нагрузку q для простоты можно заменить одиночной нагрузкой Q. Она будет располагаться ровно посередине отрезка. Находится по формуле: Q = (q × a). Делаем расчет и узнаем, чему равна Q = 2 × 2 = 4 кН.

Сила P не принадлежит ни к одной из плоскостей, а находится как бы между ними. Поэтому ее раскладывают на две составляющие: P_x и P_y. Это не значит, что они делят ее пополам. Для ее разложения понадобится вспомнить закон Пифагора. P_x = P × cos α, P_y = P × sin α.

После всех этих преобразований схема балки примет следующий вид:

Теперь можно выписывать силы по принадлежности:

Как видно из уравнения момента сил, за точку вращения балки принята опора B. Поэтому значение воздействия в килоньютонах умножается на расстояние до этой точки в метрах.

Теперь в каждом уравнении есть одна неизвестная, поэтому, подставив известные значения, можно их найти:

X_B = P × cos α = 20 × cos 30 0 = 20 × 0,866 = 17,32 кН;

R_A = М + P × sin α × b – G × (b + 0,5 × a) + Q × (a + b) × (1,5 × a + b) = 4 + 20 × sin 30 0 × 3 – 10 × (3 + 0,5 × 2) + 4 × (2 + 3) × (1,5 × 2 + 3) = 2,33 кН;

Задача 2

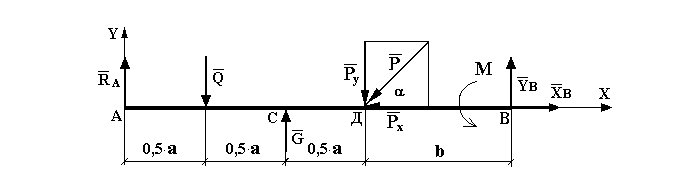
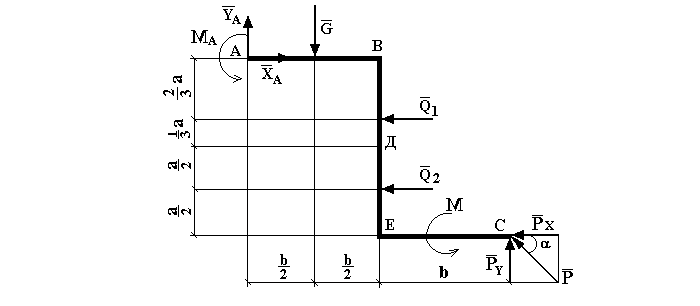
Для заданной плоской рамы определить реакции опор. Значения сил возьмем из задачи №1, несколько изменим их распределение. Схема балки показана на рис. 3.

В этом примере существует только одна опора в точке А, распределенная нагрузка имеет сложную форму. Остальные силы, а точнее их проекции на оси х и у не претерпевают каких-либо изменений.

Чтобы правильно разложить нагрузку q, ее разделяют на две: Q₁ в виде треугольника от В до Д и на Q₂, представляющей собой прямоугольник.

Соответственно, определяться они тоже будут по-разному:

Q₁ = (q × a) / 2 = (2 × 2) / 2 = 2 кН;

Q₂ = q × a = 2 × 2 = 4 кН.

Обе эти силы будут расположены посередине своих отрезков (Q₁ из характера нагрузки на 1/3 от точки Д).

В предыдущем примере шаровая опора могла вращать балку вокруг себя, поэтому не имела момента вращения. В данном случае опора представляет собой жестко закрепленную опору, поэтому имеет ко всему прочему еще и момент М_А.

После всех преобразований схема балки будет следующей:

Теперь можно приступать к выписыванию сил:

∑М_В = M_A – G × 0.5 × b – Q₁ × 2/3 × a – Q₂ ×1,5 × a + M + P × sin α × 2b – P × cos α × 2a.

Две силы Р в последнем уравнении связаны с формой самой балки, которая может испытывать момент вращения от каждой из них.

Теперь можно подставлять уже известные значения:

X_A – 2 – 4 – 20 × cos 30 0 = 0 → X_A = 23,32 кН;

Y_A – 10 + 20 × sin 30 0 = 0 → Y_A = 0 кН;

M_A – 10 × 0,5 × 3 – 2 × 2/3 × 2 – 4 ×1,5 × 2 + 4 + 20 × sin 30 0 × 2 × 3 – P × cos 30 0 × 2 × 2 = 0 → M_A = 34,95 кН.

Источник

Сила реакции опоры: определение и формула

Второй и третий законы Ньютона

Прежде чем рассматривать определение силы реакции опоры, следует вспомнить о том, что вызывает движение тел.

Причиной нарушения механического равновесия является действие на тела внешних или внутренних сил. В результате этого действия тело приобретает определенное ускорение, которое вычисляется с помощью следующего равенства:

Вам будет интересно: Понятие о равноускоренном движении. Формулы перемещения и скорости. Равноускоренное вращение

Эта запись известна как второй закон Ньютона. Здесь сила F является результирующей всех действующих на тело сил.

Если одно тело воздействует с некоторой силой F1¯ на второе тело, то второе оказывает действие на первое с точно такой же по абсолютной величине силой F2¯, но она направлена в противоположном направлении, чем F1¯. То есть справедливо равенство:

Вам будет интересно: «Тлетворный» — это о разложении

Эта запись является математическим выражением для третьего ньютоновского закона.

При решении задач с использованием этого закона школьники часто допускают ошибку, сравнивая эти силы. Например, лошадь везет телегу, при этом лошадь на телегу и телега на лошадь оказывают одинаковые по модулю силы. Почему же тогда вся система движется? Ответ на этот вопрос можно правильно дать, если вспомнить, что обе названные силы приложены к разным телам, поэтому они друг друга не уравновешивают.

Сила реакции опоры

Сначала дадим физическое определение этой силы, а затем поясним на примере, как она действует. Итак, силой нормальной реакции опоры называется сила, которая действует на тело со стороны поверхности. Например, мы поставили стакан с водой на стол. Чтобы стакан не двигался с ускорением свободного падения вниз, стол воздействует на него с силой, которая уравновешивает силу тяжести. Это и есть реакция опоры. Ее обычно обозначают буквой N.

Сила N называется нормальной потому, что она всегда направлена перпендикулярно плоскости поверхности.

Если говорить о третьем законе Ньютона, то в примере выше со стаканом воды на столе вес тела и нормальная сила N не являются действием и противодействием, поскольку обе они приложены к одному телу (стакану с водой).

Физическая причина появления силы N

Как было выяснено выше, сила реакции опоры препятствует проникновению одних твердых тел в другие. Почему появляется эта сила? Причина заключается в деформации. Любые твердые тела под воздействием нагрузки деформируются сначала упруго. Сила упругости стремится восстановить прежнюю форму тела, поэтому она оказывает выталкивающее воздействие, что проявляется в виде реакции опоры.

Многим может показаться странным, что стакан с водой способен деформировать стол, но это так. Деформация настолько мала, что невооруженным глазом ее невозможно наблюдать.

Как вычислять силу N?

Сразу следует сказать, что какой-то определенной формулы силы реакции опоры не существует. Тем не менее имеется методика, применяя которую, можно определить N для совершенно любой системы взаимодействующих тел.

Методика определения величины N заключается в следующем:

При составлении динамического уравнения следует внимательно и правильно расставлять знаки действующих сил.

Найти реакцию опоры можно также, если пользоваться не понятием сил, а понятием их моментов. Привлечение моментов сил справедливо и является удобным для систем, которые имеют точки или оси вращения.

Далее приведем два примера решения задач, в которых покажем, как пользоваться вторым ньютоновским законом и понятием момента силы для нахождения величины N.

Задача со стаканом на столе

Выше уже был приведен этот пример. Предположим, что пластиковый стакан объемом 250 мл наполнен водой. Его поставили на стол, а сверху на стакан положили книгу массой 300 грамм. Чему равна сила реакции опоры стола?

Запишем динамическое уравнение. Имеем:

Учитывая, что плотность воды равна 1 г/см3, и 1 мл равен 1 см3, получаем согласно выведенной формуле, что сила N равна 5,4 ньютона.

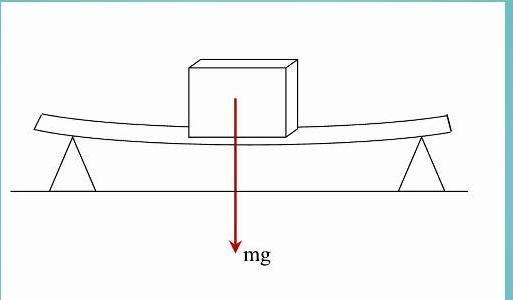
Задача с доской, двумя опорами и грузом

Доска, массой которой можно пренебречь, лежит на двух твердых опорах. Длина доски равна 2 метра. Чему будет равна сила реакции каждой опоры, если на эту доску посередине положить груз массой 3 кг?

Прежде чем переходить к решению задачи, следует ввести понятие момента силы. В физике этой величине соответствует произведение силы на длину рычага (расстояние от точки приложения силы до оси вращения). Система, имеющая ось вращения, будет находиться в равновесии, если суммарный момент сил равен нулю.

Возвращаясь к нашей задаче, вычислим суммарный момент сил относительно одной из опор (правой). Обозначим длину доски буквой L. Тогда момент силы тяжести груза будет равен:

Момент силы реакции опоры будет равен:

Поскольку система находится в равновесии, то сумма моментов должна быть равной нулю. Получаем:

N = m*g/2 = 3*9,81/2 = 14,7 Н

Заметим, что от длины доски сила N не зависит.

Учитывая симметричность расположения груза на доске относительно опор, сила реакции левой опоры также будет равна 14,7 Н.

Источник

Как определить реакции в опорах?

Автор: Константин Вавилов · Опубликовано 03.02.2016 · Обновлено 15.05.2018

Привет! В этой статье, предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции в опорах, и этому уделяют особое внимание на термехе. А курс термеха, по традиции, читают до сопромата. Для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Что такое реакция опоры?

Реакция опоры – это та сила, которая возникает в опоре от действия внешней нагрузки. В зависимости от конструкции опоры и ее назначения, в ней может появляться разное количество реакций, это может быть как сила, так и момент.

В начале этой статьи, расскажу о том, что должен уже уметь читатель, для успешного освоения данного урока. Если у Вас есть проблемы по поднятым вопросам на старте статьи, переходите по ссылкам на другие материалы на нашем сайте, после чего возвращайтесь к нам на чай реакции. Во второй части статьи, посмотрим, как вычисляются реакции на простейшем примере – балки, загруженной по центру сосредоточенной силой. Тут я покажу, как пользоваться уравнениями равновесия статики, как их правильно составлять. Дальше по плану, научу учитывать распределенную нагрузку, на примере той же балки. И завершать данный урок, будет пример определения реакций для плоской рамы, загруженной всевозможными типами нагрузок. Где применим уже все фишки, о которых я буду рассказывать по ходу урока. Что же, давайте начнем разбираться с реакциями!

Что вы должны уже уметь?

В этом блоке статье, я расскажу, как и обещал, что Вы должны УЖЕ уметь, чтобы понять то, что я буду докладывать дальше, про реакции опор.

Должны уметь находить сумму проекций сил

Да, это то, что Вам когда-то рассказывали на термехе, как собственно, и опорные реакции. Если Вы шарите немного в этих проекциях, то можете смело переходить к следующему пункту. Если же нет, то специально на этот случай, у меня есть другая статья, про проекции сил. Переходите, просвещайтесь, после чего, обязательно, возвращайтесь сюда!

Должны уметь составлять сумму моментов относительно точки

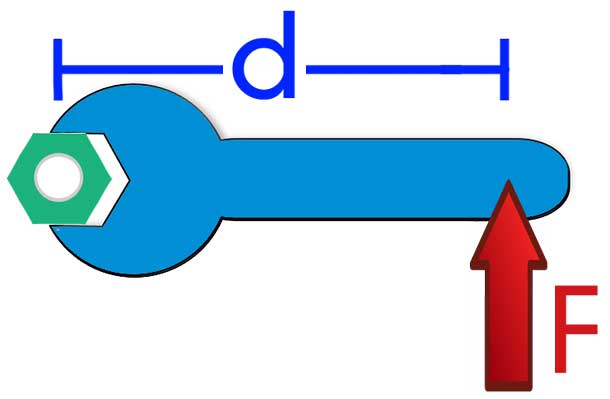
Немного теории! Познакомимся для начала с самим понятием момент силы. Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр. Проиллюстрирую написанное:

На изображении показано, как определить момент силы F, относительно точки O.

Так же, для моментов, нужно задаться каким-то правилом знаков. Сила относительно точки может поворачивать как по часовой стрелке, так и против нее. Я в своих уроках буду придерживаться такого правила:

Причем, это правило условно! Какое правило Вы будете использовать совсем не важно, результат получите тот же самый. В теоретической механике, к примеру, делают также как я рассказываю.

Должны разбираться в основных видах опор

Теперь поговорим о самих опорах. В этой статье, будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

Шарнирно-подвижная опора препятствует вертикальному перемещению элементу конструкции, в связи с чем, в ней, под действием внешней нагрузки возникает вертикальная реакция. Обозначают ее обычно как R_i, где i — точка крепления опоры.

Шарнирно-неподвижная опора имеет две реакции: вертикальную и горизонтальную. Так как препятствует перемещению в этих двух направлениях.

Вообще-то способов закрепления элементов конструкций и их условных обозначений достаточно много, но в рамках этой статьи их рассматривать не будем.

Примеры определения сил реакций опор

Вроде, всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнем с простейшей расчетной схемы балки.

Определение реакций опор для балки

Возьмем балку на двух опорах, длиной 2 метра. Загрузим ее, посередине пролета, сосредоточенной силой:

Для этой расчетной схемы, выгодно записать такое условие равновесия:
То есть, будем составлять две суммы моментов относительно опорных точек, из которых можно сразу выразить реакции в опорах. В шарнирно-неподвижной опоре горизонтальная реакция будет равна нулю, ввиду того, что горизонтальные силы отсутствуют. Последним уравнением, взяв сумму проекций на вертикальную ось, сможем проверить правильность нахождения опорных реакций, это сумма должна быть равна нулю.

Введем систему координат, пустим ось х вдоль балки, а ось y вертикально. Обозначим реакции в опорах как R_A и R_B:

Запишем уравнение моментов, относительно точки А. Сила F поворачивает ПО часовой стрелки, записываем ее со знаком МИНУС и умножаем на плечо. Сила R_B поворачивает ПРОТИВ часовой стрелки, пишем ее со знаком ПЛЮС и умножаем на плечо. Все это приравниваем к нулю:

Из полученного уравнения выражаем реакцию R_B.

Первая реакция найдена! Вторая реакция находится аналогично, только теперь уравнение моментов записываем относительно другой точки:

После нахождения реакций, делаем проверку:

Определение реакций опор для балки с распределенной нагрузкой

Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно свернуть до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:

Определение опорных реакций для плоской рамы

Теперь, после освоения азов по расчету реакций, предлагаю выполнить расчет плоской рамы. Для примера, возьмем раму, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:

Для такой расчетной схемы, лучше использовать следующую форму условий равновесия:

Составив первое уравнение, относительно точки A, сразу найдем реакцию в опоре B:

Записав второе уравнение, сумму проекций на ось х, найдем горизонтальную реакцию H_A:

И, наконец, третье уравнение, позволит найти реакцию R_A:

Не пугайтесь отрицательного значения реакции! Это значит, что при отбрасывании опоры, мы не угадали с направлением этой силы.

Расчет же показал, что R_A, направленна в другую сторону:

В итоге, получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумму будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!

На этом заканчиваю данный урок. Если у Вас остались какие-то вопросы по нахождению опорных реакций, смело задавайте их в комментариях к этой статье. Обязательно на все отвечу!

Спасибо за внимание! Если понравилась данная статья, расскажите о ней своим одногруппникам, не жадничайте 🙂

Также рекомендую подписаться на наши соц. сети, чтобы быть в курсе обновлений материалов проекта.

Источник