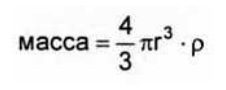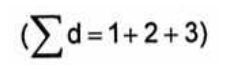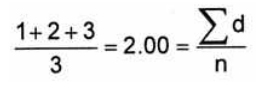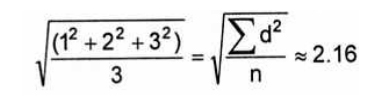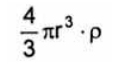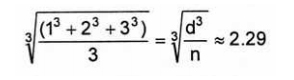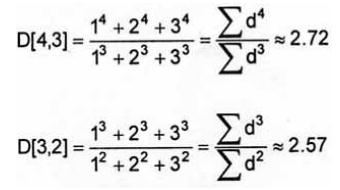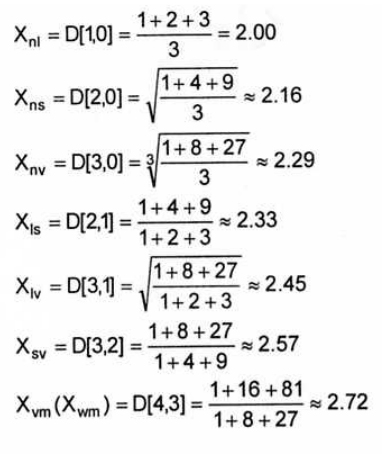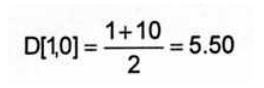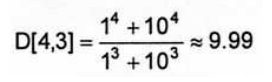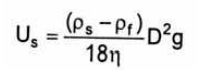в чем измеряется размер частиц
Спросите Итана: насколько малы элементарные частицы?
Размер, длина волн и шкалы температур/энергий, соответствующие различным частям электромагнитного спектра
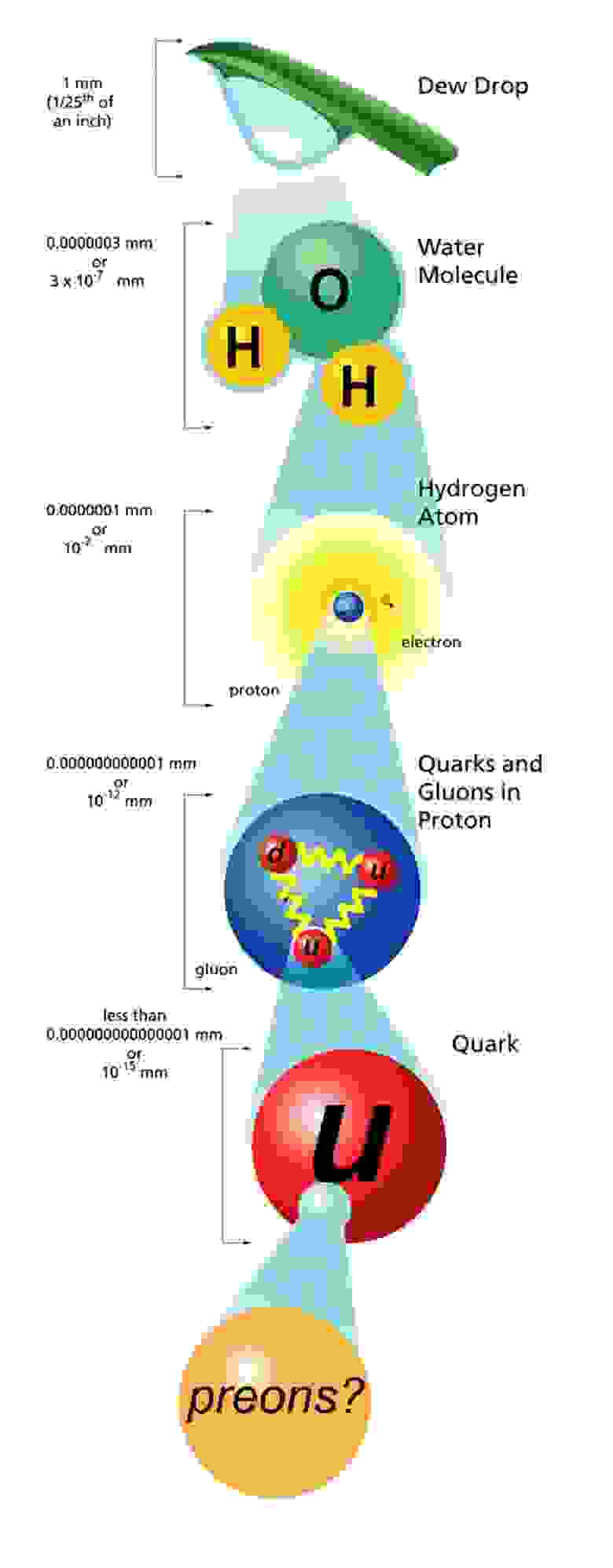
Если взять любое количество материи, сколь угодно малое или большое, то по поводу его состава будут только две возможности: либо его можно разделить на что-то поменьше, либо оно фундаментально и неделимо. Большую часть XIX века мы считали, что атомы и есть те самые фундаментальные мельчайшие сущности, поскольку греческое слово ἄτομος и означает буквально «неразрезаемый». Но теперь мы знаем больше, и можем делить атомы на ядра и электроны, а ядра можно делить не только на протоны и нейтроны, но и они сами могут быть разделены на более фундаментальные кварки и глюоны. Но откуда нам вообще известен их «размер»? Наш читатель спрашивает:
Что учёные имеют в виду, говоря о размере элементарной частицы?
Размер – понятие сложное, но квантовая механика спешит нам на помощь.
Молекула пентацена через атомный микроскоп IBM с разрешением в 1 атом
Изображение вверху было сделано методом, не сильно отличающимся от обычной фотографии – и это фото отдельных атомов внутри относительно простой молекулы. То, что свет – это волна, позволяет делать фотографии объектов определённого размера, но не чего угодно с размером сколь угодно малым. У света есть определённая длина волны, поэтому он может взаимодействовать с тем, что примерно равно или больше этой длины, но не меньше. Именно поэтому:
• Нам нужны относительно большие антенны для улавливания радиоволн, поскольку их длины волн требуют антенн значительного размера.
• Отверстия в дверце микроволновки не дают волнам выходить наружу – их длины волн больше размеров отверстий.
• Почему крохотные крупинки пыли в космосе способны отлично блокировать коротковолновый (голубой) свет, хуже блокируют более длинные волны (красные) и совершенно прозрачны для ещё более длинных волн (инфракрасных).
Слева – видимый диапазон, справа – инфракрасное фото глобулы Barnard 68
Чтобы измерить размеры мельчайших частиц, требуются фотоны всё меньшей и меньшей длины волны. Поскольку энергия фотона и его длина волны обратно пропорциональны друг другу, вам нужно всё больше и больше энергии, чтобы заглядывать в меньшие масштабы.
Но использование фотонов – не единственный вариант. Возможно использовать любые частицы высоких энергий для зондирования размеров материи. Одно из забавных правил квантовой механики состоит в том, что вести себя как волны могут не только частицы света, но и вообще все частицы – включая и такие составные, как протоны, и невидимые (пока что), как электроны. Добравшись до высоких энергий и совершив столкновение с неподвижной мишенью, мы можем либо определить размер частицы, не являющейся фундаментальной, пронаблюдав за её распадом, или же определить, что если частица не фундаментальная, она продемонстрирует это свойство только при размерах, меньших какого-то определённого.
Именно такая техника позволила нам определить, что:
Но мы уже знаем, что это не так. Эта величина оказалась намного больше размера протона, примерно на три порядка. Иначе говоря, частицы, которые мы находим, оказываются по природе своей истинно квантовыми, а это значит, что если мы будем подниматься до сколь угодно больших энергий, то истинно фундаментальные частицы должны быть точечными.
Величины в ФЭЧ и их единицы измерения
Размеры
Фемтометр в миллион раз меньше нанометра — типичного размера молекул. Размер протона или нейтрона как раз составляет примерно 1 фм. Существуют составные частицы, размер которых еще меньше; например, ипсилон-мезон, состоящий из кварк-антикварковой пары b–анти-b, имеет размер примерно 0,2 фм. Другие частицы (называемые фундаментальными), например кварки, электроны, нейтрино и т. д., пока считаются точечными; если они и имеют внутреннюю структуру, то эта структура проявится при размерах, меньших, чем тысячная доля фемтометра.
Времена
В отличие от расстояний, характерные времена, использующиеся при описании превращений элементарных частиц, могут быть самые разные.
Когда два протона сталкиваются в коллайдере, именно в течение этого промежутка времени происходит рождение некоего высокоэнергетического сгустка материи и его распад на конечные частицы. Однако сами рожденные частицы могут жить намного дольше. Например, адроны, распадающиеся за счет слабого взаимодействия, живут пикосекунды, наносекунды и иногда даже больше. Рекордсмен тут нейтрон, чье время жизни в свободном состоянии составляет примерно 15 минут. Относительно большое время жизни этих частиц вызвано тем, что распадаются они не за счет сильного, а за счет слабого или электромагнитного взаимодействия. Такие частицы успевают пролететь до распада большие дистанции — миллиметры, метры и больше; эти метастабильные частицы регистрируются непосредственно в детекторе. Частицы, распадающиеся за счет сильного взаимодействия (так называемые адронные резонансы), живут в течение адронного масштаба времени. Такие частицы до детектора не долетают, и они изучаются по следам своего распада.
Энергии
Явления, происходящие внутри ядер и элементарных частиц, сопровождаются гораздо большими изменениями энергии. Здесь уже используются мегаэлектронвольты (МэВ, 10 6 эВ), гигаэлектронвольты (ГэВ, 10 9 эВ) и даже тераэлектронвольты (ТэВ, 10 12 эВ). Например, протоны и нейтроны движутся внутри ядер с кинетической энергией в несколько десятков МэВ. Энергия протон-протонных или электрон-протонных столкновений, при которых становится заметна внутренняя структура протона, составляет несколько ГэВ. Для того чтобы родить самые тяжелые из известных на сегодня частиц, топ-кварки, требуется сталкивать протоны с энергией около 1 ТэВ.
Шкалу энергий можно также связать и со шкалой времен: E = h/T. Физический смысл этого соотношения в квантовой механике таков: процесс, сопровождающийся неопределенностью энергии E, длится примерно в течение времени T. Например, если частица распадается в течение типичного адронного масштаба времени, то неопределенность ее массы составляет порядка 1 ГэВ.
Массы
Частота событий
Обсуждая вероятность того или иного процесса на коллайдере, физики обычно приводят две величины: сечение процесса и светимость коллайдера. Именно их произведение определяет, насколько часто происходит столкновение того или иного типа на данном коллайдере.
Светимость — это «инструментальная» характеристика коллайдера, характеризующая интенсивность пучков. Светимость зависит от количества частиц в каждом пучке и от того, насколько плотно частицы собраны. Чем больше светимость, тем чаще происходят столкновения частиц из встречных пучков.
Далее, частота, с которой детектор будет регистрировать данный тип событий, обычно меньше частоты, с которой это событие происходит. Так получается потому, что вовсе не на каждое событие детектор «срабатывает» нужным образом, то есть у детектора неидеальная эффективность регистрации. Например, родившиеся частицы могут пролететь мимо детектора и избежать регистрации (впрочем, благодаря высокой герметичности современных детекторов вероятность этого мала). Либо энергия частицы одной из частиц может оказаться маленькой, и детектор просто не учтет эту частицу, примет ее за случайный шум. Либо детектор может неправильно идентифицировать рожденную частицу, приняв ее за другую и на основании этого отбросив событие как неинтересное.
Все эти процессы необходимо учитывать при сравнении реально полученных данных с теоретическими расчетами. Обычно это делается путем сложного численного моделирования процессов, протекающих внутри детектора при прохождении сквозь него частиц.
Наконец, число событий, отобранных для анализа какого-то конкретного процесса (то есть та статистика, на основе которой физики, например, заявляют об открытии новой частицы), обычно намного меньше числа реально зарегистрированных событий этого типа. Дело в том, что обычно искомые события происходят довольно редко, и их приходится вылавливать из мешанины самых разнообразных фоновых процессов. Для того чтобы увеличить надежность результатов, физики обычно отбирают только самые четкие события-кандидаты, наиболее непохожие на последствия фоновых процессов. Подробнее про эту методику см. в популярной статье Анатомия одной новости, или Как на самом деле физики изучают элементарные частицы.
Контрактное производство
Косметических средств, БАД к пище, фасовка пищевой продукции.
Определение размера частиц
Что такое частица, как определить ее размеры и для чего? На контрактном производстве ООО «КоролевФарм» в аналитической лаборатории знают ответ на этот вопрос.
В чем же загадка? Размер частицы это контролируемое линейное измерение индивидуальной частицы, которое можно определить одним из существующих и подходящих методов измерения. Представьте, что нам надо определить размер коробка с помощью линейки. Полученные результаты можно выразить в виде трех чисел: 20 * 10 * 5мм. Мы не сможем записать эту величину одним числовым значением и дать ответ: размер коробка, например, 20мм. Это будет только одно из значений, которое определяет длину коробка. Поэтому, никак невозможно выразить длину, высоту и ширину одним каким-то числом. Вот это и является основной задачей измерения размеров частиц. А как же можно выразить размер какой-нибудь частицы только одним числовым значением, у которой есть несколько величин, характеризующие ее?
Сфера является единственной формой объекта, которая может быть описана только одним числом. Только сказав, что диаметр сферы 40 мкм, и это даст полную информацию о ее размерах. А вот куб охарактеризовать точно таким же образом никак нельзя, потому что это значение (40 мкм) может относиться как к длине ребра так и к диагонали.
 |
| Рис. 1 Песчаные зерна, отличающиеся между собой и формой, и размером |
На рисунке 1 показаны несколько песчаных зерен. Глядя на рисунок, невозможно однозначно дать ответ, какого они размера, так как с разных сторон у них будут разные размеры.
Если рассмотреть нашу песчинку под микроскопом, то мы увидим ее в плоскостной проекции, и при этом измерим несколько ее диаметров. И каждое из этих значений будет характеризовать эту частицу. Значения этих диаметров будут отличаются друг от друга. Вот поэтому, тут очень важно понимать, что в основе каждого метода определения размера частиц, лежит измерение различных характеристик частицы (объем, площадь поверхности, максимальная и минимальная длина и т.д.). Конечные полученные результаты будут везде разными. И все зависит от того, каким методом измеряли разные физические характеристики частицы. На самом деле, можно сравнивать лишь только те показатели, которые были получены одним методом измерения для одного и того же материала.
Дисперсность – степень раздробленности, которая определяется величиной, обратной размеру частиц: чем больше частицы, тем меньше дисперсность и наоборот, чем меньше частицы, тем больше дисперсность. Дисперсность имеет очень важное значение как технологический показатель в производстве фармацевтических и косметических средств, БАДов и многих других мелкозернистых и порошкообразных продуктов. Так на контрактном производстве ООО «КоролевФарм» при производстве косметических средств и БАДов (таблетированных, капсулированных форм) обязательно учитывают этот параметр. Размеры частиц сырьевых компонентов, входящих в состав продукции, влияют на многие параметры, такие как: прессуемость, насыпную плотность, уплотняемость. Вот сейчас уже почти установлено, что, чем меньше концентрация в таблетной массе компонента, тем его частицы должны быть мельче. И невозможно получить однородную таблетную массу, состоящую из компонентов, которые резко отличаются друг от друга размерами частиц.
Существуют различные методы дисперсного анализа: ситовой, седиментационный, микроскопия, лазерная дифракция. Полученные результаты в ходе измерений будут отличаться друг от друга, так как каждый из этих методов измеряет разные параметры, характеризующие частицу.
 |
| Рис. 2 Анализатор А50 для определения размера частиц ситовым методом |
Седиментационный метод является самым традиционным методом дисперсионного анализа. Его используют в лакокрасочной промышленности. Результаты, которые получают этим методом, заранее неточны (занижены). Вот из-за этого многие производители, для которых так важна достоверная информация, получают неверные значения. Этот метод применяют для размера частиц узкого диапазона (от 2 до 15 мкм).
Микроскопия. В микроскоп можно видеть сами частицы, их форму, размеры. Этим методом можно судить о качестве дисперсии и о присутствии в ней агломератов.
Лазерную дифракцию (точнее Low Angel Laser Light Scattering (LALLS)) применяют в промышленности во многих отраслях. Большая часть лазерных анализаторов дают возможность определять размер частиц в интервале от 0.1 до 2000мкм.
Рис. 3 Принцип операции просеивания сыпучих материалов
1 – направление увеличения размера сит;
2 – загрузка исследуемого материала;
3 – путь продвижения материала.
При производстве косметики, БАД таблетированных или капсулированных форм, подготовленный к рассеву материал сотрудники аналитической лаборатории производства ООО «КоролевФарм» засыпают на верхнее сито. Попадая на сито, материал транспортируется по спирали, перемещаясь от периферии сита, и одновременно подбрасывается вверх. Частицы материала крупностью меньше отверстий в сетке просыпаются на следующее сито, а более крупные остаются на поверхности сетки (рис. 3).Анализатор состоит из вибропривода и просеивающей части, установленной на платформу вибропривода. Просеивающая часть анализатора состоит из сита, крышки, поддона и деталей крепления. При включении электродвигателей вибропривода его платформа с установленным на ней диском, а вместе с ней просеивающая часть анализатора, совершает возвратно-поступательные вертикальные винтовые колебания.
Материал, прошедший через отверстия первого сита, аналогичным образом рассеивается на следующем сите на два класса по крупности и так далее. Самый мелкий материал попадает в поддон.
По величине частиц порошки делят на:
После проведения испытания инженер-химик выдает протокол испытаний с полученными результатами. В протоколе также указывает о соответствии или несоответствии данного образца показателям, заявленным в нормативной документации. Результаты испытаний поступают в отдел контроля качества. В случае положительного результата, сырье допускается в дальнейшую работу на производство. В случае если результаты не соответствуют заявленным требованиям, сырье возвращается обратно поставщику.
Основные принципы анализа размеров частиц
Dr. Alan Rawle (Доктор Алан Роул)
На первый взгляд кажется, что вопрос элементарный. Однако он является основополагающим для понимания результатов, получаемых различными методами анализа размеров частиц.
Проблематика определения размеров частиц.
Стандартная задача по определению размера спичечного коробка при помощи линейки. Один из вариантов ответа: размеры коробка 20х10х5 мм. Неверно будет сказать, что размер коробка 20мм, поскольку это лишь одно из числовых значений, определяющее длину. Не так просто охарактеризовать 3-х мерный объект (коробок) одним числовым значением. Очевидно, что задача определения размера, например, песчинки или частицы пигмента, находящейся в емкости с краской, ещё сложнее.
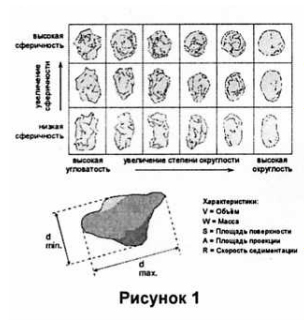
Очевидно, что начальник ОТК заинтересован в получении единственного числового значения, которое будет исчерпывающе характеризовать интересующие его частицы, то есть фактически, он должен знать увеличится или уменьшится средний размер частиц, например, с момента выпуска последней партии продукции. Это и является основным вопросом при анализе размеров частиц – как корректно охарактеризовать одним числовым значением размер 3-х мерного объекта? На рис 1. показаны несколько зерен песка. Какого они размера?
Только объект сферической формы может быть охарактеризован одним числовым значением. Достаточно сказать, что диаметр сферы 50 мкм, и это даст исчерпывающую информацию о её размере. Охарактеризовать куб таким же образом уже невозможно, поскольку значение 50мкм может относиться как к длине ребра, так и диагонали. Однако, в том числе и для спичечного коробка существует ряд свойств, которые могут быть охарактеризованы единственно возможным числом. Это, например, масса, объем или площадь поверхности. Таким образом, обладая инструментарием для определения массы коробка, можно полученную массу рассмотреть как массу шара и, учитывая что:
В зависимости от формы объекта, использование данного приближения приводит к проявлению некоторых интересных эффектов, что наглядно иллюстрируется на примере цилиндра и эквивалентной ему сферы. (Рис. 2). Изменение формы или размеров цилиндра приводит к изменению его объема/массы, и и лишь посредством эквивалентной сферы можно оценить уменьшение/увеличение объекта.
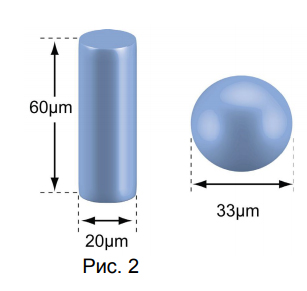
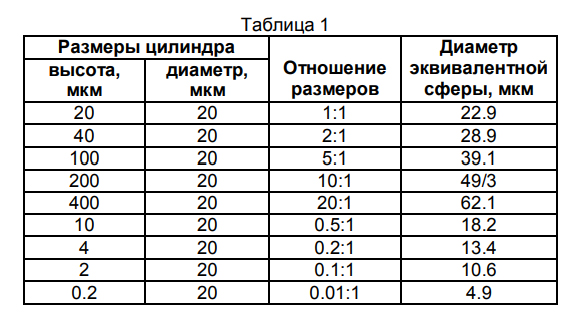
Диаметр сферы эквивалентной цилиндру с размерами 100х20мкм
Возьмем цилиндр, диаметр которого D1=20мкм, (т.е r=10мкм. Существует сфера с диаметром D2 эквивалентная цилиндру по объему. Диаметр такой сферы вычисляется следующим образом:
Таким образом, диаметр эквивалентной сферы, эквивалентной по объему цилиндру с высотой 100мкм и диаметром 20 мкм равно примерно 40мкм. В таблице 1 приведены диаметры сфер, эквивалентных цилиндрам с различными высотами. Значения последних строк таблицы характерны для больших частиц глины, имеющих форму диска. Например, при визуализации частицы диаметром 20мкм и толщиной всего 0.2мкм, толщиной можно пренебречь. Анализатор в этом случае дает результат около 5мкм.
Как следствие, вполне естественным является вопрос о сравнении результатов различных методов гранулометрического анализа.
Стоит обратить внимание, что в случае ситового анализа при использовании апкртуры 25мкм результат будет следующим, “все частицы образца меньше 25мкм”. При анализе методом лазерной дифракции ”цилиндры окажутся другого размера”, поскольку физически измеряется другой параметр.
При анализе частицы под микроскопом визуализируется её плоская проекция, и в этом случае охарактеризовать частицу можно посредством ряда различных размерных параметров. Это могут быть максимальный и минимальный диаметр(линейный размер), диаметры Ферета и Мартина и т.д., каждый из которых дает значение ”размера” частицы. Важно понимать, что каждый метод определения размера основан на измерение различных физических характеристик частиц (максимальная длина, минимальная длина, объем, площадь поверхности и т. д.), и, как следствие, размеры, полученные разными методами, будут различаться.
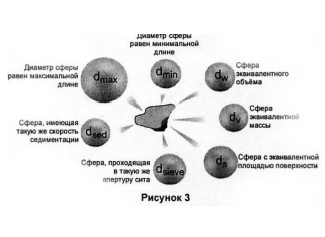
На Рис. 3 показаны различные варианты ответов на вопрос, что есть размер частицы? При этом, ошибочных результатов нет – каждый ответ субъективно корректен – он отображает физически измеряемую характеристику. Грубой аналогией будет следующее сравнение длины и ширины спичечного коробка, измеренных при помощи метрической и дюймовой линейки.
Таким образом, практически корректно сравнивать только результаты измерений, в которых один и тот же материал анализируется одним и тем же методом. Это, также, означает, что не может существовать стандартных образцов (размера) для таких частиц как зерна песка. Для возможности сравнения различных методов стандартные образцы должны быть сферическими. Стандартные образцы могут использоваться для сравнения результатов, полученных различными приборами, использующих один метод измерения.
Производные диаметры: D[4,3] и т.д.
Возьмем три сферы, диаметры которых соответственно 1,2, и 3 единиц. Каков средний размер этих сфер? Самым очевидным ответом является ”2,00”. Как получен этот результат. Сумма значений всех диаметров:
Поделенных на количество частиц (n=3). Так получается среднее (штучное или количественное) значение (среднее арифметическое значение длины), т.к. в уравнении фигурирует количество частиц: Средний диаметр:
В математике это значение называется D[1,0], т.к. в числителе уравнения – значение диаметров в первой степени (d-1 ), а в знаменателе – число частиц (диаметры в нулевой степени d0 ).
Это среднее (поверхностное) арифметическое значение (вычисленное из средней площади поверхности). Т.к. в знаменателе стоит количество частиц, а в числителе сумма квадратов диаметров, то обозначение данного диаметра – D[2,0]. Наиболее актуальным для инженера химика будет сравнение образцов по их массе. Поскольку масса шара:
то для получения среднего диаметра необходимо возвести диаметры в куб, просуммировать, разделить не количество частиц и извлечь кубический корень:
И вновь мы получаем среднее (объемное) арифметическое значение (вычисленное из среднего объема/массы), т.к. взвешивание в уравнении идет на количество частиц. Математическое определение этого среднего D[3,0].
Основной проблемой при вычислении этих ”простых” средних, D[1,0], D[2,0], D[3,0], является присутствие количества частиц в формуле расчета. Это приводит к необходимости подсчета большого количества частиц. Обычно определение количества осуществляется в случаях низкой концентрации частиц (в диапазоне ppm или ppb) в приложениях контроля чистоты/загрязнения. Например, в 1 грамме образца SiO2 (плотностью 2,5 г/см2) может содержаться около 7,6х10-11 частиц размером 1мкм.
Таким образом, необходимо перейти к понятию взвешенных (моментальных) средних, самыми широкораспространенными из которых являются:
D[3,2] – средневзыешенный на площадь поверхности – средний диаметр Саутера (Sfuter Vtfn Diameter, SMD)
Фактически, эти средние:
Являются центрами масс для функций плотности распределений в единицах объема/массы или площади поверхности соответственно. Очевидным преимуществом данного метода вычисления средних и распределения является независимость от количества частиц. Методом лазерной дифракции изначально вычисляется объемное распределение, вследствие чего столь большое внимание уделяется параметру D[4,3].
Различные методы анализа – разные средние
Метод лазерной дифракции позволяет получить значение D[4,3) или средний диаметр сферы эквивалентного объема. Это идентично среднему размеру сферы с эквивалентной массой, при условии постоянства плотности.
Таким образом, каждый метод анализа размеров частиц позволяет получать разные значения средних диаметров, в зависимости от того какой характеризующий параметр измеряется. Не удивительно, что эта ситуация может являться причиной недоумения – поскольку фактически существует бесконечное множество различных ”правильных” размеров. Ниже приведены вычисления среднего диаметра трех сфер с диаметром 1,2 и 3 единицы, и все ответы являются ”правильными” (n – количество, l – линейный размер, s – площадь поверхности, v – объем, w – масса):
Количественное и объемное распределение
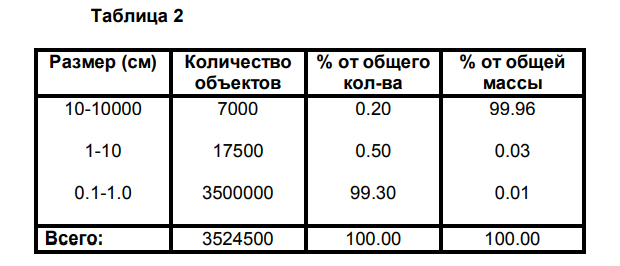
Описываемый в данной главе пример взят из статьи, опубликованной в журнале New Scientist (октябрь 1991). В космическом пространстве, на околоземной орбите находится большое количество объектов, которые регулярно регистрируются. Эти объекты классифицированы в группы по размерам.
Данные третьей колонки Таблицы 2 позволяют сделать, (корректное), заключение о том, что практически все частицы (> 99%) чрезвычайно малы. Это оценка данных на основе количества частиц. Однако, данные четвертой колонки позволяют сделать, (так же корректное), заключение о том. Что практически все частицы находятся в диапазоне 10-1000см. Т.е. частицы с такими размерами составляют практически 100% массы всей выборки. Т.е. частицы с такими размерами составляют, практически 100% массы всей выборки. Стоить отметить КОЛИЧЕСТВЕННОЕ (штучное) и МАССОВОЕ (объемное) распределения принципиально отличаются друг от друга, и каждое из них по-своему характеризует систему частиц.
И в этом случае ни одно из распределений нельзя считать неправильным. Это лишь результаты различных способов обработки и представления данных. Например, при проектировании космического модуля, можно лишь учесть, что вероятность попадания 7 000 крупных объектов, составляющих 99.96% всех частиц (по массе), ничтожно мала. Однако намного важнее учесть и предусмотреть защиту обшивки от ударов мелких частиц, количественная доля которых составляет 99.3%.
Среднее значение данных распределений сильно различаются и составляют около 1.6 см (среднее количественное) и 505 см (среднее массовое) для количественного и массового распределения соответственно.
Взаимные преобразования средних различных распределений
Как было показано ранее (раздел ”Различные методы анализа – различные средние”), при анализе частиц методом электронной микроскопии, в качестве среднего первично получается D[1,0] – среднее арифметическое значение (условно, линейного размера). Объемное или массовое среднее возможно получить посредством перерасчета. Математически это преобразование элементарно, однако стоит подробнее остановиться на последствиях подобных операций.
Предположим, относительная погрешность определения среднего размера методом электронной микроскопии составляет ± 3%. Поскольку среднее массовое является функцией третьей степени диаметра, то относительная ошибка конечного результата при преобразовании среднего арифметического (количественного) в среднее объемное (массовое) может составить до ± 9%.
В случае изначального получения объемного или массового распределения (лазерная дифракция), ситуация отлично от описанной выше. При анализе частиц, находящихся в суспензии, и при постоянной циркуляции этой суспензии через измерительную кювету, относительная ошибка может составлять не более ±0,5%. При этом относительная ошибка среднего количественного, полученная посредством преобразования из среднего объемного, составит менее 1%.
На практике это означает, что при необходимости получения объемного массового распределения по результатам микроскопии, эффект неучета одной частицы размером 10мкм, будет равносилен потере одной тысячи частиц с размером 1мкм. Таким образом, необходимо учитывать возможные последствия взаимных преобразований.
Измеряемые и производные диаметры
Метод лазерной дифракции позволяет получить объемное распределение (в случае приближения Фраунгофера, это фактически распределение площадей проекции) частиц по размерам по данным измеряемой угловой зависимости интенсивности рассеянного света. На основании объемного распределения возможно вычисление среднего для количественного распределения или распределения в единицах линейного размера (длины).
Какое значение использовать?
Принимая во внимание, что разные методы измеряют различные свойства, (т.е. размеры), частиц, а так же возможность получения различных средних ( D[4,3], D[3,2]> и т.д., вполне естественным является вопрос о том, какой же параметр следует использовать. Рассмотрим простую систему, состоящую из двух шарообразных золотых частиц диаметрами 1 и 10 единиц. Вычисление среднего арифметического диаметра дает:
Данный параметр более адекватно характеризует массу системы и представляет непосредственный интерес, например, для технологов химического производства.
В качестве другого примера. Рассмотрим производство пластин из кремния или арсенида галлия в чистом помещении. В этом случае каждая частица, попавшая на поверхность пластины, может привести к появлению дефекта и, таким образом, очень актуальной становится информация о концентрации или количестве частиц в чистой комнате, (т.к. одна частица = 1 дефект). Здесь предпочтительно использовать метод измерения количества или концентрации частиц, который принципиально отличен от анализа размеров. Эти примеры наглядно демонстрируют разницу между измерением количества частиц и их размеров. Счетчики частиц, в отличие от анализаторов размеров частиц, позволяют регистрировать каждую частицу и производить их подсчет – в этом случае размеры не так важны и достаточным может оказаться небольшое количество измеряемых классов. При анализе размеров частиц абсолютное их количество менее важно, чем размеры и распределение по размерам, и для более объективной оценки в данном случае требуется большее число размерных классов.
При исследовании работы ингалятора, предназначенного для больных астмой, важны как концентрация лекарственного препарата, так и распределение частиц по размерам.
Среднее значение, медиана и мода – элементарная статистика
Определение этих трех понятий, следующие:
Среднее значение
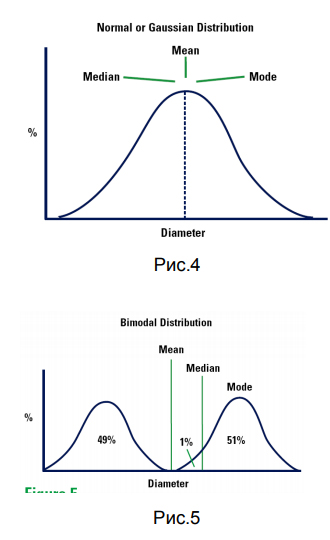
Результат усреднения данных. Существуют различные средние, которые можно вычислить для набора частиц 9D[4,3] и т.д., например, для конкретного распределения – это математические ожидание/среднее арифметическое).
Это значение размера частиц, которое делит популяцию на две равные части, т.е точка на кривой распределения, слева и справа от которой находится по 50%распределения.
Положение максимума кривой распределения, или наиболее часто встречающейся в популяции частиц размер.
Для нормального распределения среднее, мода и медиана совпадают (Рис.4)
Данный пример демонстрирует, что среднее, мода и медиана – совершенно разные диаметры, которые совпадают или близки лишь в исключительных случаях.
Как было отмечено ранее, каждый метод определения размера основан на измерении определенной характеристики частиц, и, как следствие, размеры, получаемые разными методами, различны. Далее будут подробно рассмотрены преимущества и недостатки некоторых из наиболее часто используемых методов анализа.
При ситовом анализе невозможно исследовать эмульсии и аэрозоли/спреи.
Довольно проблематичен процесс измерения сухих порошкообразных материалов с частицами менее 400# (38мкм). Мокрый анализ частично решает эту проблему, но воспроизводимость получаемых результатов очень низка и выполнение такого анализа – задача достаточно трудоемкая.
Сложно измерять связанные и агломерированные материалы, например глины.
Ситовой анализ таких материалов как TiO2 c частицами размером порядка 0,3мкм – просто невозможен. Так же метод не обладает высокой разрешающей способностью.
Результат ”занижается” при увеличении времени измерения, поскольку частицы, имеющие чуть вытянутую или игольчатую форму, при продолжительном просеивании ориентируются и проходят через сито. Поэтому время измельчения и способ просеивания (встряхивание или вибрация) необходимо четко соблюдать в регламентированных рамках.
При ситовом анализе вытянутых, игольчатых или плоских частиц не воспроизводится истинное значение весового распределения. Это может служить причиной получения необъективных результатов, например, при анализе частиц парацетамола в фармацевтической промышленности.
Традиционны метод гранулометрического анализа, используемый в лакокрасочной промышленности и при производстве керамики, результаты которого, как правило, занижены. В зависимости от ряда факторов, диапазон применимости данного метода 2-50мкм[1,2]. Принцип измерения основан на использовании закона Стокса и регистрации установившейся, (предельной), скорости оседания:
Для проведения седиментационного анализа может использоваться различный инструментарий от пипетки Андреасена (Andreason ) до центрифуг и рентгеновских анализаторов.
При анализе приведенного уравнения стоит обратить внимание на следующее. Во-первых, необходимо знать плотность дисперсной фазы. Частицы должны оседать, что не подходит для сидементационно-устойчивых эмульсий. Метод затруднителен для систем, где дисперсная фаза имеет высокое значение плотности (очень высокую скорость оседания) или состоит из смеси материалов различной плотности.
Получаемый результат – диаметр Стокса (DST – величина отличная от D[4,3]) есть диаметр сферы, с такой же скоростью седиментации, что и у исследуемой частицы. При измерении необходим точный контроль температуры, поскольку, вязкость среды (стоящая в знаменателе уравнения), зависит от температуры, (порядка 2% отклонения на 1ºС).
При помощи уравнения несложно определить время седиментации. Например, при седиментации в воде, при температуре 20ºС, частица SiO2 (r=2,5 г/см2 ) диаметром 1мкм пройдет 1 см за 3,5 часа. Таким образом само измерение является довольно длительным, а повторы весьма затруднительными. Для оптимизации анализа целесообразно увеличить g. Недостатки этого подхода рассматриваются в работе [3]. Более подробный критический анализ метода проведен в [2].
Закон стокса справедлив только для сферических частиц и при условии, что в процессе оседания исключаются столкновения между частицами. Подавляющее большинство реальных частиц по форме отличны от сферической и, таким образом, за счет большей поверхности и повышенного, (по сравнению со сферой), лобового сопротивления будут седиментировать медленнее, чем сферы эквивалентного диаметра, (что приводит к артефактному занижению получаемых результатов).
Для частиц, имеющих форму диска, как например каолины, этот эффект выражен гораздо сильнее и заранее можно ожидать существенных отклонений конечных результатов от реальных, в сторону занижения размеров
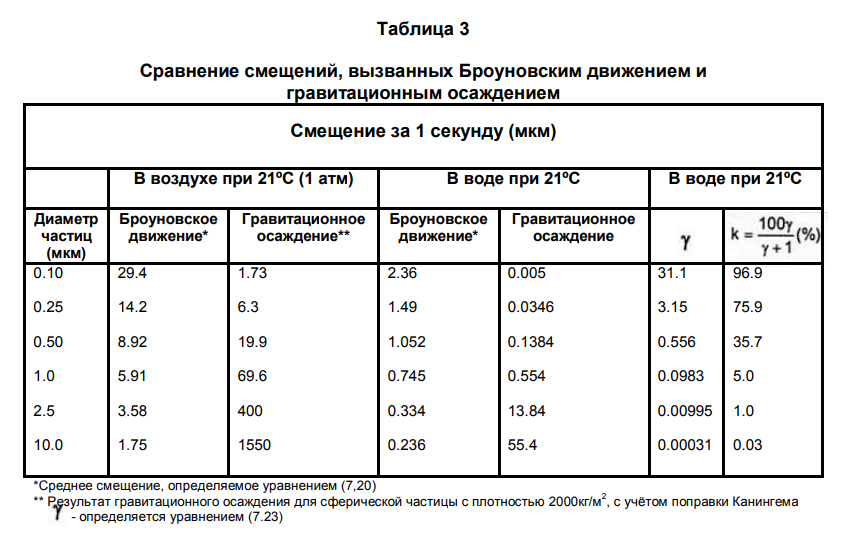
Кроме того, при проведении анализа тонкодисперсных частиц седиментационным методом необходимо учитывать Броуновское движение. Закон Стокса применим только к гравитационному осаждению частиц. В Таблице 3 приведено сравнение вклада этих двух ”конкурирующих” процессов: седиментации и Броуновского движения. Ошибка при седиментационном анализе частиц размером менее 2мкм составляет 20%, а для частиц с размером 0,5мкм может доходить до 100%.
Седиментационный анализ дает заниженный результат, и поэтому некоторые производители, осознанно используют этот метод, получая, однако, заведомо недостоверную информацию. В заключение отметим основные недостатки метода:
Время анализа. В среднем время анализа составляет от 25 минут до 1 часа, что обусловливает сложность повторных измерений и высокую вероятность агломерации материала во время измерения.
Точный контроль температуры. Необходима качественная термостабилизация системы для предотвращения температурных неоднородностей и изменения вязкости.
Невозможность получения корректных результатов при анализе смеси материалов различной плотности – а краски обычно состоят из смеси частиц самого красителя и наполнителя/добавок.
Использование рентгеновского излучения в некоторых анализаторах.
На Рис. 6 показана ожидаемая разница результатов, полученных методами седиментации и лазерной дифракции.
Кондуктометрический метод (электронный или метод Культера)
Этот метод анализа был разработан в середине 1950-х для определения размеров клеток крови, которые являются практически мономодальной суспензией в разбавленном электролите. Принцип работа приборов достаточно прост. Через калиброванное отверстие в стеклянном сосуде (трубке) протекает разбавленная суспензия, м к ней прикладывается разность потенциалов. При прохождении частицы через отверстие, скачкообразно меняется емкость, что выражается импульсом или пиком напряжения. Высота пика сравнивается с высотой пика стандартного образца. Таким образом, метод является сравнительным, требующим калибровки. Корректировка результатов, связанная с ориентацией частиц, проходящих через отверстие, возможна за счет вычисления площади под пиком, а не высоты пика. Для клеток крови это прекрасный метод определения и количественного и объемного распределения. Однако, с точки зрения анализа других материалов существует ряд серьезных ограничений:
Сложно анализировать эмульсии. Невозможность анализа аэрозолей и порошкообразных материалов непосредственно в сухом виде – необходимость диспергирования в жидкости.
Необходима калибровка при помощи дорогостоящих стандартных образцов, размер которых зависит от среды [2].
Анализ полидисперсных образцов занимает много времени, требует смены калиброванного отверстия (для покрытия широкого размерного диапазона) и чреват закупориванием отверстия крупными частицами.
Нижняя граница анализируемого размерного диапазона определяется величиной самого маленького отверстия, анализ в области менее 2мкм затруднителен. Измерение частиц TiO2 с размерами до 0,2мкм попросту невозможно.
Значительная ошибка результатов имеет место при анализе пористых материалов.
Комплексы на базе (автоматизированные), микроскопа и ПО для обработки изображений, в случае анализа достаточного количества частиц, позволяют избежать субъективизма оператора и могут давать чрезвычайно полезную количественную информацию.
Принципиально анализатор состоит из следующих основных узлов:
Лазер или источник когерентного излучения с постоянной длиной волны. Газовые HeNe лазеры ( =0.63мкм) обладают на сегодняшний день наилучшими характеристиками с точки зрения стабильности и чистоты сигнала. Стоимость, размеры и качество полупроводниковых лазеров с меньшей длиной волны в последнее время позволяет их рассматривать, и как вспомогательные и как основные источники.
Детектор. Обычно используется многоэлементная кремниевая фотодиодная матрица. Детектор с хорошим динамическим диапазоном, состоящий из 32-44 элементов, обеспечивает оптимальное разрешение, при этом увеличение количества элементов, как показала практика, не приводит к увеличению реального разрешения Основные принципы анализа размеров частиц
Находясь в кювете, (в зоне измерения, на пути лазера), частицы рассеивают свет. Индикатриса рассеяния, (угловая зависимость интенсивности рассеянного излучения), определяется размером частиц, их оптическими характеристиками и длиной волны лазера (которая является постоянной). Измерение индикатрисы и последующая обработка результатов позволяет определить характер распределения частиц по размерам, (дисперсный состав), данной системы.
Экспериментальные значения индикатрисы рассеяния получаются в результате усреднения данных о светорассеянии, регистрируемых с частотой 1кГц. Установив программно длительность анализа около 20 секунд, фактически выполняется 20 000 измерений. Ни один из традиционных методов дисперсного анализа, (Седиментационный, ситовой, микроскопия), не позволяют за такой короткий промежуток времени выполнять такое количество измерений. Кроме того, при исследовании, например, суспензий и эмульсий, за 1 минуту все исследуемые частицы успевают пройти через измерительную кювету много раз, что обеспечивает получение устойчивых и в высокой степени воспроизводимых результатов. Огромным преимуществом такой скорости анализа, становится возможность не только контроля необходимой дисперсности материала, но и наблюдение в режиме реального времени за процессами агломерации, например при наличии возможности ультразвуковой обработки суспензии.
Процедура восстановления распределения частиц по размерам по данным угловой зависимости рассеянного света, (деконволюция), производится ПО анализатора на основании оптической модели:
Приближение Фраунгофера является частным случаем теории Ми, в основе которого лежат следующие допущения:
Размер частиц значительно больше длины волны используемого света (ISO13320 позиционирует около 25мкм, при этом нижняя граница диапазона корректного анализа порядка 3мкм при использовании He-Ne лазера).
Частицы различных размеров рассеивают свет с одинаковой интенсивностью.
Итак, можно отметить следующие преимущества метода лазерной дифракции:
Метод основан на фундаментальных принципах. Калибровка прибора, конструктивно реализованного в соответствии с ISO13320, не требуется. Можно лишь проверить качество функционирования анализатора, посредством измерения стандартных образцов, (верификация).
Широкий динамический диапазон. Инструментарий позволяет измерять размеры частиц в диапазоне от 0,1 до 2000мкм. Частицы меньшего размера, (1нм – 1мкм), анализируют методом динамического светорассеяния, (фотонной корреляционной спектроскопии), и результаты будут объективными до тех пор, пока в системе преобладает хаотическое Броуновское движение, и частицы не седиментируют.
Универсальность. Возможность анализа суспензий, эмульсий, порошкообразных материалов в сухом виде, аэрозолей и спреев. Например, возможно измерять гранулометрический состав красок и лаков, распыляемых форсунками различного типа. В частности, это используется разработчиками форсунок и пульверизаторов для достижения необходимого размера распыляемых частиц, путем оптимизации вязкости, давления и размеров выпускных отверстий. Методика анализа нашла широкое применение во множестве отраслей производственной и исследовательской деятельности [4,5, 6, 10]. Один из стандартов ASTM посвящен анализу спреев методом лазерной дифракции.
Возможно непосредственное измерение гранулометрического состава сухих порошков, однако, не для любой системы можно добиться качественного диспергирования. Наряду с анализом суспензий, результат может оказаться информативным для оценки количества агломерированного материала в сухой фазе.
Измерение частиц суспензий и эмульсий происходит через рециркуляцию пробы через измерительную кювету, что позволяет получать высокую воспроизводимость результатов, использовать диспергирующие добавки и поверхностно-активные вещества, (например, Калгон, Твин и др.), для оптимизации диспергирования.
Анализируется весь образец. Несмотря на малое количество, необходимое для анализа материала, (обычно 4-10г для сухого измерения и 1-2г для мокрого).ю весь материал проходит через луч лазера и учитывается вклад каждой частицы. С учетом объёмов исследуемых образцов, особое внимание стоит уделять представительности пробоотбора.
Метод не разрушающий не инвазивный. При определённых условиях, например, дорогостоящие образцы могут быть восстановлены и использованы после анализа.
Изначально получаемым является результат в виде объемного распределения, которое при условии постоянства плотности эквивалентно массовому. А это именно то распределение, которое наиболее информативно для инженерахимика или технолога.
Скорость получения результатов достаточно высока, (менее одной минуты). Это обуславливает возможность быстрой обратной связи для оптимизации технологических процессов и простоту повторных измерений.
Высокая надежность и повторяемость результатов. Это обеспечивает гарантию того, сто изменившийся показатель характеризует именно изменение характеристик продукта и не является следствием «приборного дрейфа».
1. Lambourne R., Strivens T.A. (ed.) Paint and surface coatings: Theory and practice (2nd ed.). Woodhead Publishing Ltd. 1999. ISBN 1 85573 348 X; ISBN-13: 978 1 85573 348 0
2. Allen T. Particle Size Measurement (5th ed.). Chapman & Hall. 1997. ISBN 0 412 75350 2
3. Beckers G.J.J., Veringa H.J. Some restrictions in particle sizing with the Horiba CAPA-500. Powder Technology. 1990, 60(3): 245-248
4. Ranucci J. Dynamic plume-particle size analysis using laser diffraction. Pharmaceutical Technology. 1992, 16:108-114
5. Hind G. Manufacturing Chemist. August 1990: 28-30
6. Wedd M.W. ILASS-Europe 8th Annual conference, Koninklijke/Shell Laboratorium, Amsterdam 30th September – 2nd October, 1992
7. Hatch T., Choate S.P. Statistical description of the size properties of non-uniform particulate substances. J. Franklin Inst. 1929, 207: 369-387
8. Irudayaraj J., Reh C. (ed.) Nondestructive Testing of Food Quality. Wiley-Blackwell Publishing. November, 2007. ISBN: 978-0-8138-2885-5