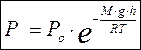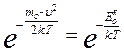в чем измеряется распределение молекул по высотам

04.01.202407.04.2022 admin 0 Comments

Закон распределения молекул по высоте

На молекулы реального газа действует поле тяготения Земли. При этом давление газа, обусловленное полем тяготения Земли и тепловым движением молекул, убывает с увеличением высоты на величину .

Решая это уравнение, получим;

Учитывая, что на уровне моря h₁ = 0; Р₁ = Р_о = 760 мм рт ст,

получим Барометрическую формулу (зависимость давления газа от высоты)

Из основного уравнения МКТ Р = n k T, концентрация может быть выражена через давление . Тогда можно записать:

где: n и n_o — концентрация молекул газа на высоте h и h_o

Тогда Распределение Больцмана (распределение молекул по высоте)

Из формулы следует, что на высоте h концентрация молекул (плотность газа) уменьшается с уменьшением температуры. При Т = 0 n = 0, т.е. при температуре абсолютного нуля все молекулы располагались бы на поверхности Земли.

Между распределением Больцмана и Максвелла большое сходство в основном множителе:

Распределение Максвелла

Распределение Больцмана

где и — кинетическая и потенциальная энергия молекулы;

§ 6. Реальные газы. Уравнение Ван-дер-Ваальса

Для реальных газов необходимо учитывать размеры молекул и их взаимодействие друг с другом, поэтому модель идеального газа и уравнение Клапейрона — Менделеева pV_m=RT (для моля газа), описывающее идеальный газ, для реальных газов непригодны.

Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И. Ван-дер-Ваальс (1837—1923) вывел уравнение состояния реального газа. Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.

1. Учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не V_m, а V_m — b, где b — объем,занимаемый самими молекулами.

Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в расчете на одну молекулу.

2. Учет притяжения молекул. Действие сил притяжения газа приводит к появлению дополнительного давления на газ, называемого внутренним давлением. По вычислениям Ван-дер-Ваальса, внутреннее давление обратно пропорционально квадрату молярного объема, т. е.

где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, V_m — молярный объем.

Вводя эти поправки, получимуравнение Ван-дер-Ваальса для моля газа(уравнение состояния реальных газов):

Для произвольного количества вещества v газа (v=m/M) с учетом того, что V=vV_m, уравнение Ван-дер-Ваальса примет вид

где поправки а и b — постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и b).

Изотермы Ван-дер-Ваальса.

При высоких температурах (T > T_к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре T_к изотерма имеет одну точку перегиба К. Ей соответствуют V_к и р_к.

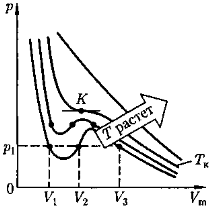
При низких температурах (Т

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник

Савельев И.В. Курс общей физики, том I

Загрузить всю книгу

Титульный лист

Главная редакция физико-математической литературы

Механика, колебания и волны,

КУРС ОБЩЕЙ ФИЗИКИ, ТОМ I

Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.

Предисловие к четвертому изданию

При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.

Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.

Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.

Ноябрь 1969 г. И. Савельев

Из предисловия к четвертому изданию

Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.

При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.

Источник

Московский государственный университет печати

Физика. Часть 1. Механика. Молекулярная физика и термодинамика

Курс лекций

Так как все направления скорости молекул равновероятны, то на первый взгляд кажется, что и все величины скорости должны быть равновероятны. Однако, как показывает эксперимент, при каждой температуре Т существует такая скорость (наиболее вероятная), что большинство молекул газа движется со скоростями, не очень сильно отличающимися от нее. Молекулы, скорости которых много больше или много меньше наиболее вероятной встречаются редко.

Тогда вероятность того, что мы встретим такую скорость,

» />

Так как в системе молекул скорость изменяется непрерывно, то можно определить более точно функцию распределения f(v) :

» />

Функция f(v) должна быть нормирована условием:

» />

Интегрирование до » /> не означает, что в газе есть молекулы с бесконечно большими скоростями, это вычислительный прием, который возможен потому, что молекул с очень большими скоростями очень мало.

Функция распределения молекул газа по скоростям была получена Дж. Максвеллом. Он решил задачу для газа, состоящего из очень большого числа п одинаковых молекул, находящихся в состоянии беспорядочного теплового движения при определенной температуре. Предполагается, что силовые поля, действующие на газ, отсутствуют. Максвелловский закон распределения по скоростям имеет вид:

» />

При повышении температуры кривая распределения молекул по скоростям деформируется.

» />

2) стационарно (не меняется во времени), несмотря на то, что в результате столкновений молекулы все время меняют величину скорости.

Знание статистических функций распределения дает возможность вычислять средние значения микроскопических параметров, не зная их значений у отдельных молекул. Например, среднюю арифметическую скорость движения молекул можно найти, вычислив интеграл:

» />

Если подставить f(v) и проинтегрировать, то получим среднюю скорость молекул идеального газа:

» />

Для нахождения средней квадратичной скорости нужно вычислить интеграл:

» />

мы получим уже известное выражение

» />

Экспериментальное измерение скоростей молекул (одним из первых такой опыт осуществил О. Штерн с использованием молекулярных пучков) показало хорошее согласие с теоретическими значениями скоростей, которые дает распределение Максвелла. В своих экспериментах по изучению термоэлектронной эмиссии Ричардсон в 1921 г. проверил закон распределения скоростей Максвелла. В состоянии равновесия над поверхностью металла образуется насыщенный пар из электронов, экспериментальное определение скоростей электронов подчиняется закону Максвелла.

В газе существует некоторое в среднем неизменное во времени распределение молекул по скоростям.

Равновесное состояние газа характеризуется не только распределением молекул по скоростям, но и по координатам. В отсутствие внешних полей это распределение будет однородным, т.е. газ равномерно распределяется по всему объему сосуда: в любых равных макроскопических объемах внутри сосуда в среднем находится одинаковое число молекул. А как обстоит дело при наличии действующего на молекулы поля, например, поля тяжести?

Найти закон распределения молекул газа с высотой в однородном поле тяжести можно из условия механического равновесия.

» />

Условие механического равновесия выделенного слоя газа

» />

то условие равновесия принимает вид

» />

Из уравнения Клапейрона-Менделеева для произвольной массы газа m

» />

Тогда из уравнения (12.1) с учетом, что предел отношения » /> при » /> есть производная » />, получаем

» />

Решение такого уравнения при постоянных g и Т имеет вид

» />

Значение постоянной С определяется из условия, что давление на высоте h = 0 равно величине » />:

» />

Учитывая связь между давлением газа и концентрацией молекул

получим распределение молекул по высоте во внешнем поле (поле силы тяжести):

» />

Вместо силы тяжести ( » />) на частицы может действовать и другая сила, например, центробежная или электростатическая. Поэтому в общем случае барометрическая формула имеет вид:

» />

1. Каково распределение молекул газа по скоростям в равновесном состоянии?

2. Что такое функция распределения случайной величины, например скорости молекул?

3. Постройте график функции распределения Максвелла по скоростям. Что происходит с кривой функции распределения с ростом температуры?

4. Какие опыты подтверждают выводы теории о распределении молекул по скоростям?

5. Как, пользуясь функцией распределения, найти среднюю скорость движения молекул? Среднюю квадратичную скорость движения молекул?

6. Дайте определение наиболее вероятной скорости движения молекул.

7. Напишите закон распределения молекул в поле тяготения.

8. При какой температуре средняя квадратичная скорость молекул кислорода больше их наиболее вероятной скорости на 100 м/с?

Источник

В чем измеряется распределение молекул по высотам

Если в жидкости находятся в большом количестве маленькие частички, более тяжелые, чем жидкость, и не растворяющиеся в ней, то на первый взгляд может показаться, что рано или поздно эти частицы должны опуститься на дно. Это, однако, неверно, — так было бы, если бы отсутствовало тепловое движение.

Действительно, сила тяжести тянет частицы вниз, однако хаотическое тепловое движение, являющееся неотъемлемым свойством любых частиц, будет непрерывно препятствовать действию силы тяжести. Частица движется вниз, но по дороге может испытать столкновение, которое отбросит ее кверху; опять начнется движение вниз и опять столкновение может отбросить частицу вверх или в сторону. Если какой-то частице удалось добраться до дна сосуда, то зато случайными ударами другая частица может быть поднята со дна и случайными толчками может быть доведена до высоких слоев жидкости. Вполне понятно, что в результате установится некоторое неравномерное распределение частиц. В верхних слоях частиц будет меньше, ближе ко дну сосуда — больше всего. Чем тяжелее частицы и чем меньше температура, тем больше будет «прижато ко дну» распределение частиц по высоте.

Количественная сторона этого интересного явления, которое имеет место для любых частиц, расположенных в поле тяжести (молекул газа или частиц эмульсии, взвешенных в газе или жидкости), освещается законом Больцмана. Экспоненциальный множитель в формуле распределения Больцмана перепишем в виде

вместо потенциальной энергии тяготения мы подставили ее выражение Нас интересует число всех молекул (любых скоростей), находящихся на высоте между Оно будет равно

Здесь коэффициент пропорциональности по смыслу есть не что иное, как удельное число частиц при Закон убывания частиц с высотой показан на рис. 86.

Вид формулы показывает справедливость утверждения, сделанного вышегчем больше масса частиц и чем меньше температура, тем быстрее падает кривая. Из формулы видно также, что быстрота убывания зависит от ускорения силы тяжести. На разнцх планетах частицы должны быть по-разному распределены с высотой.

Согласно приведенной формуле какое-то (пусть очень малое) число молекул имеется на любой высоте над поверхностью Земли. Это значит, что молекулы могут удаляться от Земли, улетать в

мировое пространство, так как не исключено, что случайными столкновениями то та, то другая молекула получит скорость достаточную, как известно, для ухода из сферы земного притяжения. Можно поэтому сказать, что Земля постепенно теряет свою атмосферу. Однако оценки скорости рассеяния атмосферы показывают, что она ничтожно мала. За все время существования Земли было потеряно ничтожное количество воздуха.

Другое дело на Луне, где скорость преодоления притяжения равна Такая небольшая скорость достигается молекулами с большой легкостью, поэтому на Луне нет атмосферы.

Формула убывания числа частиц с высотой может быть записана для плотности газа или для давления газа. Так как давление газа пропорционально числу частиц в единице объема, то формулу можно переписать в виде

Здесь давление на нулевом уровне. Последнюю формулу называют барометрической. С ее помощью метеорологи, производящие йзмерения атмосферного давления на больших высотах, приводят результаты своих измерений «к уровню моря».

Необходимо отметить еще одно важное применение формулы распределения частиц по высоте: она была использована французским ученым Перреном для опытного определения числа Авогадро. В соответствии с условиями опыта Перрену пришлось несколько модифицировать формулу распределения молекул по высоте. Он изучал эмульсию, получающуюся при растворении гуммигута (разновидность смолы) в воде. В этой эмульсии при помощи микроскопа можно рассмотреть целый муравейник зернышек сферической формы. При помощи центрифуги Перрен сортировал зернышки гуммигута по размеру. За несколько месяцев работы было получено зерен гуммигута диаметром 0,74 микрона. Плотность гуммигута т. е. масса одного зерна была равна

Точмгс определение размеров зерен было нелегкой задачей. Перрен выполнял это тремя независимыми способами:

1) под микроскопом определялась длина цепочки из нескольких десятков плотно прилегающих зерен;

2) взвешивалось несколько тысяч зерен и размер вычислялся через известную плотность гуммигута;

3) по формуле Стокса (см. стр. 196) из наблюдений за скоростью опускания в эмульсии облачка из зерен. При этом предполагалось, что по закону Архимеда зерно опускается под действием силы — где плотность жидкости, радиус зерна. Эта сила при равномерном опускании уравновешена силой вязкого трения, вычисляемой по формуле Стокса. Из этого условия определяется

Все три способа дали хорошо совпадающие результаты. Это означало, что действующий вес микроскопического зернышка, плавающего в жидкости, можно записать в виде Вспомним, что Отсюда получается барометрическая формула для «атмосферы» из зерен гуммигута, плавающих в воде:

Опыт сводился к определению отношения концентраций на равностоящих уровнях. Делалось это при помощи фокусирования микроскопа на достаточно тонкий слой эмульсии и подсчета числа частиц в поле зрения за одинаковые промежутки времени. Меняя вязкость эмульсии в сотни раз, Перрен неукоснительно наблюдал, что отношение концентраций соответствовало барометрической формуле. Подставляя значения можно было определить Оказалось, что, несмотря на широкие вариации вязкости эмульсии и размеров зерен, найденное таким образом блестяще совпадает со значениями, предсказанными молекулярно-кинетической теорией: Перрен получил (по современным данным Это с полной достоверностью свидетельствовало, больцмановское распределение по энергиям применимо даже к таким частицам, «грамм-молекула» которых равна 50 000 тонн!