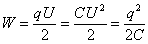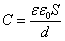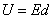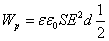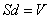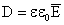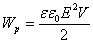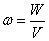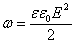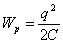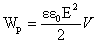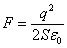в чем измеряется объемная плотность энергии магнитного поля
Плотность энергии магнитного поля
Одной из характеристик магнитного излучения, показывающей распределение его энергии в объеме пространства, является плотность энергии магнитного поля. При изучении электромагнетизма необходимо усвоить, что это за величина, что она характеризует и как измеряется.
Объемная плотность магнитной энергии
Формула нахождения объемной плотности энергии имеет такой вид:
Под ω здесь подразумевается собственно искомая плотность, под W – энергия имеющегося поля, под V – объем пространства, в котором поле проявляет активность. Если выразить значение W через магнитную проницаемость µ и индукцию В и подставить в формулу, она приобретет следующий вид:
ω=В2/2* µ0* µ (здесь µ0 – это магнитная постоянная).
Преобразование с использованием вектора индукции применяется, чтобы исключить привязку активного магнитного поля к особенностям дросселя. Формула для вычисления индукционной характеристики выглядит так:
I здесь – токовая сила в катушечной цепочке, через n выражается такая величина, как плотность обмотки. Она равна частному количества витков в соленоидной обмотке и длины фрагмента, на котором размещены витки. Тогда формула для W:
Подставив выражение в основную формулу плотности, можно привести его к ранее обозначенному виду.
Наличие магнитного поля вокруг проводника или катушки с током
При подключении соленоида (катушки) в электрическую цепь вокруг нее формируется поле. Характеристики поля зависят от ряда параметров: от средовых особенностей окружения, токовой силы (она измеряется в амперах) и материала, из которого изготовлен проводник или обмотка катушки. В полевом пространстве могут образовываться электромагнитные волны. Так как на полевой энергетический потенциал, прежде всего, оказывает влияние сила текущего в системе электротока, можно сделать вывод, что работа тока по генерированию магнитного пространства будет эквивалентной энергии последнего. Если в систему подключена катушка с магнитным сердечником, то на энергетическую плотность будет влиять полевая энергия в вакууме и в материале, из которого сделан сердечниковый элемент.
Для изучения динамики явления можно рассмотреть электроцепь, включающую в себя дроссель, лампу, замыкающий ключ и источник постоянного электротока. Когда ключик замыкается, токовый путь будет идти от «положительного» зажима источника через лампу и индуктивную катушку. Поначалу лампа накаливания загорится ярче, что связано со значительной величиной сопротивления дроссели. По мере того, как сопротивление будет падать, а проходящий через обмотку ток увеличиваться, интенсивность горения лампочки будет понижаться. Связано это с тем, что первое время подаваемый на дроссель ток имеет значение, пропорциональное току высокой частоты.
Чтобы практически построить цепь, подходящую для расчета, нужно, чтобы энергетический ресурс источника питания затрачивался на генерирование магнитного поля. Поэтому параметрами внутреннего сопротивления дроссели и питательного источника допустимо пренебрегать.
Важно! Согласно второму закону Кирхгофа, сумма подсоединенных к электрической цепи напряжений равняется сумме снижений напряжения для всех компонентов цепочки.
Измерение плотности энергии магнитных полей
Данная величина показывает энергию, содержащуюся в единице объема окружающей среды, подпадающей под влияние поля. Обозначается она греческой буквой ω. Для вычисления применяется формула:
ω=W/V, в данном случае W – это полевая энергия в объеме пространства V.
Единица измерения плотности поля в международной системе СИ тоже выглядит как частное единиц, в которых измеряются эти величины: джоулей и кубических метров (Дж/м3). Показатель для аккумуляторов (ионных, свинцово-кислотных и других) указывают в прилагающейся документации.
Для соленоида, подсоединенного в электрическую цепь, оба составляющих этого частного можно выразить через следующие единицы:
Тогда конечная формула принимает следующий облик:
Формула индуктивного сопротивления катушки
Вычислить величину сопротивления дросселя XL можно, воспользовавшись следующей формулой:
Здесь буква L обозначает параметр индуктивности дроссели, а f – токовую частоту. Исходя из этого выражения, поначалу попадающий на обмотку ток будет пропорциональным электротоку большой чистоты. В это время дроссель проявляет поведение, аналогичное ситуации цепного разрыва, с сильным повышением индуктивного сопротивления. С течением времени последнее падает до нулевого значения.
Вмонтированная в лампу нитка отличается высоким показателем сопротивления, тогда как активный показатель обмотки, напротив, стремится к нулю. Из-за этого возникает ситуация, когда почти весь цепной ток проходит через дроссель. Когда цепь размыкают при помощи ключа, лампа не затухает постепенно. Напротив, она сначала резко начинает гореть интенсивно, потом – медленно угасать. Чтобы лампа горела, требуется энергетический ресурс. Он поступает из магнитного поля, генерируемого индуктивной катушкой. Таким образом, дроссель проявляет себя источником самоиндукции.
В рассмотренном примере катушка с обмотками, подключенная в цепь, выступает как источник магнитного поля. Поскольку в такой ситуации это поле не является однородным, для выполнения расчетов необходимо использование показателя, характеризующего концентрацию и распределение энергии в поле. Можно заключить, что смысл введения параметра плотности поля состоит именно в этом.
Видео
Плотность энергии магнитного поля
Вы будете перенаправлены на Автор24
Энергия магнитного поля и плотность энергии
Магнитное поле, создаваемое токами, распределено в пространстве. Рассмотрим, какова плотность энергии поля изолированного контура с током. Используем выражение для энергии магнитного поля, которое создано контуром с током:
Примем во внимание, что магнитный поток индукции через фиксированную неподвижную площадку пропорционален силе тока, а именно:
Из формулы (2) получим, что индуктивность контура равна:
тогда энергия магнитного поля может быть представлена как:
Магнитный поток из своего определения равен:
$Ф=\int\limits_S <\vec\bullet d\vec\left( 5 \right),>$
Тогда выражение (5) приведем к виду:
Подставим выражение для магнитного потока (7) в формулу для энергии (2), найдем:
где сделан переход к объемным токам при помощи соотношения:
Готовые работы на аналогичную тему
$\vec
$\vec j$ – вектор плотности тока.
Стрелка в выражении (9) показывает, что данная замена дает возможность перейти от формул для объемных токов к формулам линейных токов и в обратную сторону.
Преобразуем выражение под интегралом так, чтобы в него входили только векторы поля и векторный потенциал. Используем формулы (6) и
Вспомним известное соотношение для дивергенции векторного произведения:
Получим в результате:
тогда выражение для энергии примет вид:
Будем считать, что все токи находятся в конечной области пространства. Тогда на больших расстояниях ($r$) от области локализации токов мы будем иметь:
Из выражения (15) следует, что объемная плотность распределения энергии магнитного поля равна:
Плотностью энергии магнитного поля называют его энергию, сосредоточенную в единице объема этого поля.
Представленное выражение справедливо для равномерного распределения энергии поля по объему.
Формула (16) говорит нам о том, что объемная плотность энергии магнитного поля в каждой его точке определяют значения векторов поля в этой точке, и не имеет значение каковы источники поля.
Для однородного изотропного магнетика мы имеем следующую связь между векторами поля:
$\vec=\mu \mu_<0>\vec
Используя формулу (17) выражения для нахождения плотности магнитного поля представим как:
В Международной системе единиц (СИ) плотность энергии магнитного поля измеряется в джоулях, деленных на кубометр ($Дж/м^3$ ).
Энергия магнитного поля при наличии магнетиков
Ограниченность формул для вычисления плотности энергии
Допущения, сделанные нами, которые заставляют говорить об ограничениях применения формул, полученных нами для плотности энергии магнитного поля:
Вопрос о локализации энергии магнитного поля
Для постоянных магнитных полей, которые создаются неподвижными постоянными токами, непонятно, где локализуется энергия. Возьмем выражение для магнитной энергии соленоида:
Однако энергию соленоида можно представить и так:
где присутствуют параметры самого соленоида и характеристика магнитного поля ($B$), что говорит о том, что энергия поля распределена по объему поля.
Для постоянных магнитных полей эта непонятность вызвана тем, что токи и поля существуют неразрывно, образуя систему.
При переходе к переменным магнитным полям приемлемой становится только полевая концепция магнитной энергии, так как переменные магнитные поля входят как компоненты электромагнитных полей и могут существовать самостоятельно от токов. Электромагнитные волны переносят энергию, значит, сделаем вывод о том, что энергия магнитного поля распределена в объеме поля.
Объемная плотность энергии магнитного и электрического полей
Электрическое поле и его свойства
Заряженные тела окружены особой средой, которая представляет собой электрическое поле. С его помощью осуществляется электрическое взаимодействие.
Электрическое поле — физическое поле, окружающее любой электрический заряд и оказывающее силовое воздействие на другие заряды, отталкивая или притягивая их.
Причинами возникновения электрического поля служат:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Электрические и магнитные поля принято рассматривать в качестве проявления обобщенного электромагнитного поля. Данное понятие связано с проявлением какого-либо из четырех фундаментальных взаимодействий природного характера.
Изучение и применение свойств электрических полей имеет большое значение в развитии физики как науки. На основе электрических полей разрабатывают электротехническое оборудование. С точки зрения атомной физики и химии, электрическое поле является силой удержания атомного ядра и электронов в атомах.
За счет данной силы формируются химические связи между атомами, что приводит к образованию молекул. Путем практического применения электрических полей удается обнаружить движения с помощью емкостных методик. Явление активно используют в диагностике и терапии в медицинской сфере.
У электрического поля есть математическое определение, согласно которому оно представляет собой векторное поле, связывающее с любой точкой в пространстве силу (электростатическую или кулоновскую) на единицу заряда, приложенную к бесконечно малому положительному пробному заряду, покоящемуся в этой точке.
В системе СИ единица измерения электрического поля: Вольт на метр (В/м), что в точности эквивалентно Ньютону на Кулон (Н/Кл).
Электрическое поле обладает следующими свойствами:
С целью раскрытия смысла понятия «электрического поля» можно рассмотреть основные его характеристики.
Напряженность — силовая характеристика электрического поля.
Напряженность, как векторная величина, обозначается Е и измеряется в Ньютонах на Кулон (Н/Кл), либо Вольтах на метр (В/м).
Найти напряженность можно по формуле:
Силовые линии — линии, касательные к которым совпадают с вектором напряженности.
Свойства силовых линий:
Электрические заряды, которые являются причиной образования электрических полей, описывают с помощью закона Гаусса. Электрические поля могут быть сформированы за счет изменения магнитных полей. В этом случае работает закон электромагнитной индукции Фарадея.
Перечисленные закономерности позволяют определить поведение электрического поля в вакуумной среде. С другой стороны, магнитное поле представляет собой функцию электрического поля. Можно выявить связь между уравнениями для обоих полей. В результате будут образованы уравнения Максвелла, описывающие магнитное и электрическое поля в виде функции зарядов и токов.
При рассмотрении частного случая стационарного состояния, то есть при наличии стационарных зарядов и токов, можно наблюдать исчезновение индуктивного эффекта Максвелла–Фарадея. Получается пара уравнений.
Закон Фарадея без индукционного члена:
\(\displaystyle \nabla \times \mathbf
\(\varepsilon _ <0>\) — электрическая постоянная.
Анализируя записанное уравнение можно сделать вывод: электрическое поле, создающее точечный заряд, в любом месте имеет направление от заряда в том случае, когда он положительный. Если заряд отрицательный — поле направлено в его сторону. Можно также заметить уменьшение величины поля пропорционально обратному квадрату расстояния от заряда.
Кулоновская сила, которая действует на заряд величиной q в какой-либо точке пространства, определяется, как произведение заряда и электрического поля в этой точке:
Уравнения Максвелла линейны. По этой причине для электрических полей характерен принцип суперпозиции. Согласно данной закономерности, полное электрическое поле в точке от распределенных в пространстве зарядов соответствует векторной сумме электрических полей, которые образованы в рассматриваемой точке отдельными зарядами.
Запись результирующего поля с помощью закона Кулона:
С помощью принципа суперпозиции можно выполнить расчет электрического поля от непрерывного распределения \(<\displaystyle \rho (<\boldsymbol
С учетом заряда \(<\displaystyle \rho (<\boldsymbol
Рассчитать полное электрическое поле можно с помощью суммы вкладов от всех малых объемов. При этом нужно воспользоваться методом интегрирования по объему распределения заряда \(<\displaystyle \rho (x')>\) :
В том случае, когда рассматривается статичная система с магнитными полями, стабильными во времени, согласно закону Фарадея, электрическое поле является потенциальным. При этом допустимо задать электрический потенциал или функцию \(\Phi.\) В результате:
Общий случай электрического поля недопустимо описывать без учета магнитного поля. При зависимости от вектора магнитного потенциала A, определенного как:
допустимо записать электрический потенциал \( <\displaystyle \Phi >\) в виде:
где \( <\displaystyle \nabla \Phi >—\) градиент электрического потенциала;
Из рассмотренного уравнения можно получить закон индукции Фарадея:
Плотность энергии электрического и магнитного полей
Энергия электромагнитного поля — энергия, которая заключена в электромагнитном поле.
В рамках данного понятия можно рассматривать частные случаи чистого электрического и чистого магнитного поля. Рассмотреть энергию электромагнитного поля допустимо с помощью его характеристик.
Работа A электрического поля E, которая совершается для перемещения заряда Q, схожа по смыслу с механической работой:
где \(U=\int E\,dx\) — разность потенциалов, или напряжение.
Чаще всего при решении примеров рассматривают непрерывный перенос заряда за определенное время между точками с конкретной разностью потенциалов U(t). В результате уравнение для определения работы принимает следующий вид:
Мощность P, которая характеризует электрический ток на отрезке цепи, равна производной от работы A по времени. Формула для расчета мощности:
Согласно закону Ома:
Электрическая мощность, которая выделяется на сопротивлении R, определяется, как:
Формула мощности с учетом напряжения принимает следующий вид:
Таким образом, работа (выделившаяся теплота) представляет собой интеграл мощности по времени:
Если рассматривать электрическое и магнитное поля, можно прийти к выводу, что их энергия пропорциональна квадрату напряженности поля. Определение «энергия электромагнитного поля» не совсем соответствует действительности. Ему на замену в физике нередко употребляют термин плотности энергии электромагнитного поля (в заданной точке пространства). Общая величина энергии поля является интегралом плотности энергии по всему пространству.
В вакуумной среде и микрополях:
где E — напряженность электрического поля;
B — магнитная индукция;
D — электрическая индукция;
H — напряженность магнитного поля;
\(\varepsilon _ <0>\) — электрическая постоянная;
\(\mu _<0>\) — магнитная постоянная.
Энергия электромагнитного поля в колебательном контуре:
где U — электрическое напряжение в цепи;
C — электроемкость конденсатора;
L — индуктивность катушки или витка с током.
В том случае, когда речь идет об электромагнитной волне, плотность потока энергии определяют с помощью вектора Пойнтинга S (в русской научной литературе можно встретить понятие вектор Умова–Пойнтинга).
В системе СИ вектор Пойнтинга определяют, как:
В результате вектор Пойнтинга равен векторному произведению напряженностей электрического и магнитного полей. Направление вектора совпадает с перпендикулярами к векторам E и H. Данное условие соответствует свойству поперечности электромагнитных волн.
С другой стороны, формулу для плотности потока энергии можно адаптировать для случая стационарных электрических и магнитных полей:
Формула объемной плотности энергии
Конденсатор представляет собой двухполюсник, значение емкости которого может быть постоянным или переменным, а проводимость обладает малыми значениями.
Конденсатор является устройством, предназначенным для накопления заряда и энергии электрического поля, и пассивным электронным компонентом. Единицами измерения емкости конденсатора являются фарады.
Принято выражать энергию заряженного конденсатора с помощью величин, являющихся характеристиками электрического поля в пространстве между обкладками.
Энергия плоского конденсатора:
Емкость плоского конденсатора:
Таким образом, напряженность поля в конденсаторе и разность потенциалов между его обкладками связаны формулой:
С другой стороны, объем конденсатора равен:
С учетом \(\overrightarrow
Объемная плотность энергии электрического поля:
Объемная плотность энергии — величина, равная энергии единицы объема поля.
В случае изотропного диэлектрика объемная плотность энергии:
Исходя из записанных уравнений, можно сделать вывод о том, что плотность энергии поля с определенной напряженностью, образованного в среде с конкретной проницаемостью, прямо пропорциональна квадрату напряженности поля.
Энергия поля конденсатора с зарядом q на его обкладке определяется с помощью величины заряда и емкости конденсатора:
Энергия электрического поля может быть определена при известной силовой характеристике поля:
В том случае, когда поле является однородным:
Между обкладками плоского конденсатора действует сила притяжения. Известно, что:
Одна пластина создает поле, напряженность которого равна:
Записанное выражение не согласуется с опытом. Причина заключается в том, что кроме «электрической силы» на обкладки со стороны диэлектрика (имеется виду жидкий или газообразный диэлектрик) действуют еще механические силы, стремящиеся их раздвинуть. Опытным путем доказано, что роль носителя энергии играет поле.
В электростатике поле и заряды невозможно отделить друг от друга. С другой стороны, электрические поля, которые изменяются по времени, могут существовать обособлено, независимо от возбудивших их зарядов, и могут распространяться в пространстве в виде электромагнитных волн, способных переносить энергию.
Единицы измерения плотности энергии
Плотность энергии магнитного поля и напряженность магнитного поля, формулы расчета
Любой электрический ток окружает магнитное поле. Нетривиальным является вопрос о локализации собственной энергии тока, – находится она в проводнике, где перемещаются заряды, или в магнитом поле (веществе, которое окружает ток)?
Ответ на заданный вопрос получают при исследовании переменных магнитных полей или электромагнитных волн. В электромагнитной волне магнитные поля, переменные в пространстве и времени, могут существовать при отсутствии токов. Мы знаем, что электромагнитные волны переносят энергию, следовательно, можно сделать вывод о том, что энергия локализуется в магнитном поле.
Объемная плотность магнитной энергии
Формула нахождения объемной плотности энергии имеет такой вид:
ω=W/V.
Под ω здесь подразумевается собственно искомая плотность, под W – энергия имеющегося поля, под V – объем пространства, в котором поле проявляет активность. Если выразить значение W через магнитную проницаемость µ и индукцию В и подставить в формулу, она приобретет следующий вид:
ω=В2/2* µ0* µ (здесь µ0 – это магнитная постоянная).
Преобразование с использованием вектора индукции применяется, чтобы исключить привязку активного магнитного поля к особенностям дросселя. Формула для вычисления индукционной характеристики выглядит так:
I здесь – токовая сила в катушечной цепочке, через n выражается такая величина, как плотность обмотки. Она равна частному количества витков в соленоидной обмотке и длины фрагмента, на котором размещены витки. Тогда формула для W
Подставив выражение в основную формулу плотности, можно привести его к ранее обозначенному виду.
Ограничения применения формулы для вычисления плотности энергии магнитного поля
Все сказанное выше предполагало, что магнитная проницаемость вещества, в котором находится поле, остается неизменной. Вся работа источника тока переходит в энергию магнитного поля. Это абсолютно точно только для вакуума. Формула для объемной плотности энергии магнитного поля в виде (4) является приближенной, так как она не учитывает точно, что поле выполняет работу при намагничивании.
Предположение о неизменности магнитной проницаемости означает, что:
Данная зависимость точна для многих веществ, парамагнетиков и диамагнетиков и неприменима для ферромагнетиков.
Применяя формулу (6) плотность энергии магнитного поля представим как:
Формулу (7), определяющую плотность энергии магнитного поля, можно использовать и для неоднородных магнитных полей.
Наличие магнитного поля вокруг проводника или катушки с током
При подключении соленоида (катушки) в электрическую цепь вокруг нее формируется поле. Характеристики поля зависят от ряда параметров: от средовых особенностей окружения, токовой силы (она измеряется в амперах) и материала, из которого изготовлен проводник или обмотка катушки. В полевом пространстве могут образовываться электромагнитные волны. Так как на полевой энергетический потенциал, прежде всего, оказывает влияние сила текущего в системе электротока, можно сделать вывод, что работа тока по генерированию магнитного пространства будет эквивалентной энергии последнего. Если в систему подключена катушка с магнитным сердечником, то на энергетическую плотность будет влиять полевая энергия в вакууме и в материале, из которого сделан сердечниковый элемент.









Для изучения динамики явления можно рассмотреть электроцепь, включающую в себя дроссель, лампу, замыкающий ключ и источник постоянного электротока. Когда ключик замыкается, токовый путь будет идти от «положительного» зажима источника через лампу и индуктивную катушку. Поначалу лампа накаливания загорится ярче, что связано со значительной величиной сопротивления дроссели. По мере того, как сопротивление будет падать, а проходящий через обмотку ток увеличиваться, интенсивность горения лампочки будет понижаться. Связано это с тем, что первое время подаваемый на дроссель ток имеет значение, пропорциональное току высокой частоты.
Советуем изучить Новые генераторы энергии
Чтобы практически построить цепь, подходящую для расчета, нужно, чтобы энергетический ресурс источника питания затрачивался на генерирование магнитного поля. Поэтому параметрами внутреннего сопротивления дроссели и питательного источника допустимо пренебрегать.
Важно! Согласно второму закону Кирхгофа, сумма подсоединенных к электрической цепи напряжений равняется сумме снижений напряжения для всех компонентов цепочки. Второй закон Кирхгофа

Второй закон Кирхгофа
Индуктивность
Электрический ток, проходящий по контуру, создает вокруг него магнитное поле. Магнитный поток Φ через контур этого проводника (его называют собственным магнитным потоком
) пропорционален модулю индукции В магнитного поля внутри контура \(\left( \Phi \sim B \right)\), а индукция магнитного поля в свою очередь пропорциональна силе тока в контуре \(\left( B\sim I \right)\).
Таким образом, собственный магнитный поток прямо пропорционален силе тока в контуре \(\left( \Phi \sim I \right)\). Эту зависимость математически можно представить следующим образом:
— коэффициент пропорциональности, который называется
индуктивностью контура
.
В СИ единицей индуктивности является генри (Гн):
Индуктивность контура зависит от размеров и формы контура, от магнитных свойств среды, в которой находится контур, но не зависит от силы тока в проводнике. Так, индуктивность соленоида можно рассчитать по формуле
L = \mu \cdot \mu_0 \cdot N^2 \cdot \dfrac,\)
где μ — магнитная проницаемость сердечника, μ — магнитная постоянная, N
— число витков соленоида,
S
— площадь витка,
l
— длина соленоида.
При неизменных форме и размерах неподвижного контура собственный магнитный поток через этот контур может изменяться только при изменении силы тока в нем, т.е.
\(\Delta \Phi =L \cdot \Delta I.\) (1)
Работа электрического поля по перемещению заряда
Понятие работы A <\displaystyle A>электрического поля E <\displaystyle E>по перемещению заряда Q <\displaystyle Q>вводится в полном соответствии с определением механической работы:
где U=∫Edx <\displaystyle U=\int E\,dx>— разность потенциалов (также употребляется термин напряжение).
Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов U(t)<\displaystyle U(t)>, в таком случае формулу для работы следует переписать следующим образом:
«Действие магнитного поля на проводник с током»
Если металлический проводник с током поместить в магнитное поле, то на этот проводник со стороны магнитного поля будет действовать сила, которая называется силой Ампера.
Сила Ампера зависит от длины проводника с током, силы тока в проводнике, модуля магнитной индукции и расположения проводника относительно линий магнитной индукции: FA = BIlsinа.
Для определения направления силы Ампера применяют правило левой руки. Если левую руку расположить в магнитном поле так, чтобы силовые линии входили в ладонь, а четыре пальца были направлены по току, то отогнутый большой палец укажет направление силы, действующей на проводник.








Магнитное взаимодействие можно наблюдать между двумя параллельными токами (опыт Ампера): два параллельных проводника с током отталкиваются, если направления токов в них противоположны, и притягиваются, если направления токов совпадают.
Экспериментальное исследование показывает, что сила Ампера прямо пропорциональна длине проводника l и силе тока I в проводнике. Коэффициентом пропорциональности в этом равенстве является модуль вектора магнитной индукции В. Соответственно, F = BIl. В таком виде зависимость силы, действующей на проводник с током в магнитном поле, записывается в том случае, если линии магнитной индукции перпендикулярны проводнику с током. Из приведённой формулы понятно, что магнитная индукция является силовой характеристикой магнитного поля.
Единица магнитной индукции = 1Н / 1А • 1м = 1 Тл. За единицу магнитной индукции принимают магнитную индукцию такого поля, в котором на проводник длиной 1 м действует сила 1Н при силе тока в проводнике 1 А.
Магнитное поле действует также на движущиеся заряженные частицы. При этом сила (сила Лоренца) зависит от модуля магнитной индукции, заряда частицы, а также от модуля и направления её скорости.
Электрический двигатель
Движение проводника с током в магнитном поле лежит в основе работы электрического двигателя. Если поместить прямоугольную рамку в магнитное поле и пропустить по ней электрический ток, то рамка повернётся, потому, что на стороны рамки действует сила Ампера. При этом сила, действующая на сторону рамки ab, противоположна силе, действующей на сторону cd.
Советуем изучить Ряд сопротивления резистора Е24
Для того чтобы рамка не остановилась в тот момент, когда её плоскость перпендикулярна линиям магнитной индукции, и продолжала вращаться, изменяют направление тока в проводнике. Для этого к концам рамки припаяны полукольца, по которым скользят контакты, соединённые с источником тока. При повороте рамки на 180° меняются контактные пластины, которых касаются полукольца и, соответственно, направление тока в рамке.
В электрическом двигателе энергия электрического и магнитного полей превращается в механическую энергию.
Действие магнитного поля на проводник с током
Конспект урока по физике в 8 классе «Действие магнитного поля на проводник с током».
Следующая тема: «Электромагнитная индукция. Опыты Фарадея».







Энергия магнитного поля при наличии магнетиков
Энергия электрического и магнитного полей
Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Строго говоря, термин «энергия электромагнитного поля» является не вполне корректным. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля
(в определённой точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству.
Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей.
В вакууме (а также в веществе при рассмотрении микрополей):
— напряжённость электрического поля,
B
— магнитная индукция,
D
— электрическая индукция,
H
— напряжённость магнитного поля,
с
— скорость света, ε<\displaystyle \varepsilon _<0>> — электрическая постоянная и μ<\displaystyle \mu _<0>> — магнитная постоянная. Иногда для констант ε<\displaystyle \varepsilon _<0>> и μ<\displaystyle \mu _<0>> — используют термины диэлектрическая проницаемость и магнитная проницаемость вакуума, — которые являются крайне неудачными, и сейчас почти не употребляются.
Энергия магнитного поля. Плотность энергии.
Энергия магнитного поля. Плотность энергии.Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля. Рассмотрим контур индуктивностью L, по которому протекает ток I. С этим контуром сцеплен магнитный поток Ф=LI, поскольку индуктивность контура неизменна, то при изменении тока на dI магнитный поток изменяется на dФ=LdI. Но для изменения магнитного потока на величину dФ следует совершить работу dА=IdФ=LIdI. Тогда работа по созданию магнитного потока Ф равна Значит, энергия магнитного поля, которое связано с контуром, Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (1) формулу индуктивности соленоида, найдем Так как I=Bl
Магнитное поле, создаваемое магнитным моментом атома, определяется этими различными формами углового момента, как и в классической физике вращающиеся заряженные объекты создают магнитное поле. Однако, наиболее значительный вклад происходит от спина. Благодаря свойству электрона как и всех фермионов подчиняться правилу запрета Паули, по которому два электрона не могут находится в одном и том же квантовом состоянии, связанные электроны спариваются друг с другом, и один из электронов находится в состоянии со спином вверх, а другой — с противоположной проекцией спина — состояние со спином вниз. Таким образом магнитные моменты электронов сокращаются, уменьшая полный магнитный дипольный момент системы до нуля в некоторых атомах с чётным числом электронов.
В ферромагнитных элементах, таких как железо, нечётное число электронов приводит к появлению неспаренного электрона и к ненулевому полному магнитному моменту. Орбитали соседних атомов перекрываются, и наименьшее энергетическое состояние достигается, когда все спины неспаренных электронов принимают одну ориентацию, процесс известный как обменное взаимодействие. Когда магнитные моменты ферромагнитных атомов выравниваются, материал может создавать измеримое макроскопическое магнитное поле. Парамагнитные материалы состоят из атомов, магнитные моменты которых разориентированы в отсутствии магнитного поля, но магнитные моменты отдельных атомов выравниваются при приложении магнитного поля.
Ядро атома тоже может обладать ненулевым полным спином. Обычно при термодинамическом равновесии спины ядер ориентированы случайным образом. Однако, для некоторых элементов (таких как ксенон-129) возможно поляризовать значительную часть ядерных спинов для создания состояния с сонаправленными спинами —состояния называемого гиперполяризацией. Это состояние имеет важное прикладное значение в магнитно-резонансной томографии.
Принято различать макро- и микро-токи. Макротоки — это токи, текущие по проводникам. В любом веществе электроны движутся по круговым орбитам. Движение электронов в атоме по круговым орбитам тоже приводит к созданию магнитного поля. Токи, создаваемые в веществах движущимися электронами называют микротоками. Гипотеза Ампера: в каждом веществе за счёт движения электронов возникают микротоки.
Молекулярные токи − токи, обусловленные движением электронов в атомах, ионах, молекулах.
Намагниченность — характеристика магнитного состояния макроскопического физического тела. Обозначается обычно М или J. Намагниченность равна отношению магнитного момента тела к его объёму.
В случае однородно намагниченного тела намагниченность определяется как магнитный момент J единицы объёма тела: J = M/V, где М — магнитный момент тела, V — его объём. В случае неоднородно намагниченного тела намагниченность определяется для каждой точки тела (точнее, для каждого физически малого объёма dV): J = dM/dV, где dM — магнитный момент объёма dV. Единица намагниченности в Международной системе единиц — ампер на метр (1 А/м — намагниченность, при которой 1 м³ вещества обладает магнитным моментом 1 А·м²), в системе СГС — эрг/(Гс·см³); 1 эрг/(Гс·см³) = 10³ А/м.
Намагниченность тел зависит от внешнего магнитного поля и температуры. У ферромагнетиков зависимость J от напряжённости внешнего поля Н выражается кривой намагничивания (см. Намагничивания кривые, Гистерезис). В изотропных веществах направление J совпадает с направлением Н, в анизотропных (см. Магнитная анизотропия) направления J и Н в общем случае различны.
Вектор намагничивания — магнитный момент элементарного объёма, используемый для описания магнитного состояния вещества. По отношению к направлению вектора магнитного поля различают продольную намагниченность и поперечную намагниченность. Поперечная намагниченность достигает значительных величин в анизотропных магнетиках, и близка к нулю в изотропных магнетиках. Поэтому, в последних возможно выразить вектор намагничивания через напряжённость магнитного поля и коэффициент названный магнитной восприимчивостью:
Магнитная восприимчивость — физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе. (Объёмная) магнитная восприимчивость равна отношению намагниченности единицы объёма вещества к напряжённости намагничивающего магнитного поля. Она является безразмерной величиной и измеряется в безразмерных единицах. Магнитная восприимчивость, рассчитанная на единицу массы вещества, называется удельной магнитной восприимчивостью. Аналогично определяется молярная магнитная восприимчивость. Магнитная восприимчивость может быть как положительной, так и отрицательной. Отрицательной обладают диамагнетики: они намагничиваются не по полю, а против поля. У парамагнетиков и ферромагнетиков она положительна (намагничивание по полю).
Магнитная восприимчивость, как правило, зависит от температуры (исключение составляют большинство диамагнетиков и некоторые парамагнетики — щелочные и, отчасти, щёлочноземельные металлы). Магнитная восприимчивость парамагнетиков уменьшается с температурой, следуя закону Кюри — Вейса. В ферромагнитных телах магнитная восприимчивость с ростом температуры увеличивается, достигая резкого максимума вблизи точки Кюри. Магнитная восприимчивость антиферромагнетиков увеличивается с ростом температуры до точки Нееля, а затем падает по закону Кюри — Вейса.
Магнитная проницаемость — физическая величина, характеризующая связь между магнитной индукцией B и магнитным полем H в веществе.
Обозначается μ. У изотропных веществ μ = B / H (в Международной системе единиц СИ).Выделяют относительную и абсолютную магнитные проницаемости где μr — относительная, а μ — абсолютная проницаемость, μ0 — магнитная постоянная.
У анизотропных тел (кристаллов) М. п. — тензор. М. п. связана с магнитной восприимчивостью c соотношением m= 1 + 4pc (в СГС системе единиц) или m = 1 +c (в ед. СИ), m измеряется в безразмерных единицах. Для физич. вакуума c = 0 и m= 1.
Магнитные материалы, магнетики — материалы, вступающие во взаимодействие с магнитным полем, выражающееся в его изменении, а также в других физических явлениях — изменение физических размеров, температуры, проводимости, возникновению электрического потенциала и т. д.
Формула индуктивного сопротивления катушки
Формула магнитного потока
Вычислить величину сопротивления дросселя XL можно, воспользовавшись следующей формулой:
Здесь буква L обозначает параметр индуктивности дроссели, а f – токовую частоту. Исходя из этого выражения, поначалу попадающий на обмотку ток будет пропорциональным электротоку большой чистоты. В это время дроссель проявляет поведение, аналогичное ситуации цепного разрыва, с сильным повышением индуктивного сопротивления. С течением времени последнее падает до нулевого значения.
Вмонтированная в лампу нитка отличается высоким показателем сопротивления, тогда как активный показатель обмотки, напротив, стремится к нулю. Из-за этого возникает ситуация, когда почти весь цепной ток проходит через дроссель. Когда цепь размыкают при помощи ключа, лампа не затухает постепенно. Напротив, она сначала резко начинает гореть интенсивно, потом – медленно угасать. Чтобы лампа горела, требуется энергетический ресурс. Он поступает из магнитного поля, генерируемого индуктивной катушкой. Таким образом, дроссель проявляет себя источником самоиндукции.
Советуем изучить Осциллограмма
В рассмотренном примере катушка с обмотками, подключенная в цепь, выступает как источник магнитного поля. Поскольку в такой ситуации это поле не является однородным, для выполнения расчетов необходимо использование показателя, характеризующего концентрацию и распределение энергии в поле. Можно заключить, что смысл введения параметра плотности поля состоит именно в этом.







Плотность энергии различных систем
В таблице приведена плотность энергии замкнутых систем, включая дополнительные внешние компоненты, такие как окислители или источники тепла, но исключая энергию покоя системы в конечном состоянии. 1 МДж ≈ 278 Вт·ч.
Плотность энергии
| Название | Плотность энергии на единицу массы (МДж/кг) | Плотность энергии на единицу массы (Вт⋅ч/кг) | Плотность энергии на единицу объёма (МДж/л) | Практическая эффективность использования % |
| Аннигиляция материя + антиматерия | до 89 875 517 873,681 764 (точно) ≈ 9⋅1010 | 24 965 421 631 578,26(7) ≈ 25⋅1012 | Зависит от вступающих в реакцию частиц, электроны и позитроны аннигилируют полностью, при аннигиляции барионов часть энергии в конечном счёте уносят нейтрино | |
| Слияние ядер водорода | 645 000 000 | 179 310 000 000 | ||
| Реакция дейтерий-тритий | 337 000 000 | 93 686 000 000 | ||
| Уран-235, используемый в ядерном оружии | 88 250 000 | 24 533 500 000 | 1 681 000 000 | |
| Природный уран (99,3 % U-238, 0,7 % U-235) в реакторе на быстрых нейтронах | 86 000 000 | 23 908 000 000 | ||
| Тепловая энергия от α-распада плутония-238 | 2 200 000 | 611 600 000 | 43 648 000 | |
| Кинетическая энергия спутника Земли на низкой орбите | 33 | 9 167 | ||
| Дизельное топливо в мощной дизельной электростанции (без учёта массы генератора) | 20,1 | 5 583 | 47 % | |
| Бензин (без учёта массы генератора) | 8,1—10,5 | 2250—2917 | 19—24 % | |
| Супермаховик | 1,8 | 500 | 98% | |
| Генератор на водородном топливном элементе, без учёта массы конструкции | 12 | 3000 | ||
| Серебряно-цинковый аккумулятор | 0,47 | 130,6 | 1,8 | |
| Литий-ионный аккумулятор | 0,46—0,72 | 128—200 | 2 | |
| Ni-MH-аккумулятор формата AA ёмкостью 2000 мА·ч | 0,33 | 92 | 1,24 | |
| Тяговый свинцово-кислотный аккумулятор | 0,17 | 47 | ||
| Пусковой свинцово-кислотный аккумулятор | 0,1368 | 38 | 0,337 | |
| 0,1 | ||||
| Ионистор | 0,03 | 6,17 | 0,032 (MAXWELL K2) | |
| Керамический конденсатор | 0,003 | |||
| Электролитический конденсатор | 0,000 639 | 0,1775 | 0,00083 | |
| Плёночный конденсатор | 0,000 180 | 0,05 | 0,0025 (maxwell CM-3) | |
| Гравитационный аккумулятор (груз 1 кг на высоте 1 м) | 0,000 009 8 | 0,0027 | 0,0001 для свинца | |
| Взведенная | 0,0003 | 0,083 | 0,0006 |
Определение магнитной энергии
Магнитная энергия и электростатическая потенциальная энергия связаны уравнениями Максвелла. Потенциальная энергия магнитного момента m m m в магнитном поле B B B определяется как механическая работа магнитной силы (фактически магнитного момента) на повторное выравнивание вектора магнитного дипольного момента и равна:
E = − m ⋅ B E = — m \cdot B E=−m⋅B
в то время как энергия, запасенная в катушке индуктивности (с индуктивностью L L L) при прохождении через нее тока I I I, определяется как:
E = 1 / 2 L I 2 E = 1/2 LI^2 E=1/2LI2
Это выражение лежит в основе сверхпроводящего накопления магнитной энергии.
Энергия также хранится в магнитном поле. Энергия на единицу объема в области пространства проницаемости μ 0 μ0 μ0, содержащей магнитное поле B B B, равна:
U = B 2 / 2 μ 0 U = B^2/2μ_0 U=B2/2μ0
В более широком смысле, если мы предположим, что среда является парамагнитной или диамагнитной и существует линейное определяющее уравнение, связывающее B B B, то можно показать, что магнитное поле хранит энергию
где интеграл оценивается по всей области, где существует магнитное поле.
Аналогично энергию магнитного поля тока можно определить также через работу тока против ЭДС самоиндукции, которая выполняется при замыкании цепи.
Сравнивая выражение энергии магнитного поля через индукцию и силу тока с формулой для определения кинетической энергии, делаем вывод, что индуктивность в электромагнитных явлениях играет такую же роль, как масса в механических явлениях, и является мерой инертности электрической цепи.