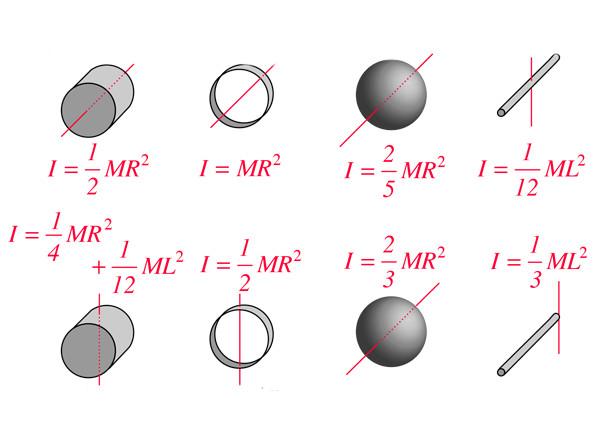в чем измеряется момент инерции плоской фигуры
Что такое момент инерции? В чем измеряется момент инерции? Пример задачи
Механика представляет собой один из основных разделов физики, в котором рассматриваются законы движения и равновесия тел. При количественном описании движения вращения важной величиной является момент инерции. В данной статье изучим эту величину. Кроме того, ответим на вопрос о том, в чем измеряется момент инерции твердого тела.
Понятие о моменте инерции для точки материальной
Как физическую величину, его определяют в виде произведения массы на квадрат радиуса вращения. Предположим, что существует некоторая материальная точка, которая имеет массу m. Она вращается вокруг оси, при этом радиус окружности равен r. При заданных условиях инерции, момент вычисляется в соответствии со следующей формулой:

Этой формулой можно пользоваться даже в случаях изучения тел со сложной формой. Главным условием справедливости равенства является наличие огромной разницы между расстоянием до оси вращения r и геометрическими размерами самого тела. Например, при расчете величины I для нашей планеты, которая вращается вокруг Солнца по круговой траектории, можно считать Землю материальной точкой, поскольку расстояние до звезды на несколько порядков превышает радиус планеты.
Величина I для тела произвольной формы
В случае, если геометрические размеры вращающегося тела незначительно отличаются от радиуса r, тогда следует принимать во внимание форму тела. С учетом названного фактора рассчитывают момент инерции с использованием следующей формулы:
По сути, это равенство является суммой моментов инерций всех материальных точек, которые образуют тело. При проведении практических вычислений, записанной формулой пользуются в несколько ином виде, который представлен ниже:
Как видно, интегрирование по массе m заменяется на интегрирование по объему V. Здесь греческой буквой ρ обозначена плотность. Если тело является однородным, то ρ будет постоянной величиной, которую можно вынести за знак интеграла. Если же масса неоднородно распределена по телу, то плотность будет функцией параметра r. Записанную формулу удобно использовать при определении I разных тел, потому что расчет выполняется с помощью мысленного деления тела на элементарные объемы dV.
Результаты применения записанного выше равенства для геометрических тел идеальной формы, например, для сферы, цилиндра или стержня, собраны в соответствующие таблицы. В чем измеряется момент инерции? Ниже на рисунке приводятся величины I для некоторых тел. Как видим, все формулы линейно зависят от массы тел и от квадрата геометрического параметра.
В чем измеряется момент инерции тела?
Получив необходимые теоретические сведения для величины I, каждый легко сможет ответить на поставленный вопрос. Действительно, если взглянуть на формулу для I материальной точки, то, отвечая на вопрос о том, в чем измеряется момент осевой инерции, следует ответить, что в килограммах на квадратный метр. Сокращенно эта единица записывается кг*м2. Очевидно, что ту же самую единицу мы получим, если воспользуемся интегральным выражением через объем и плотность.
Отметим, что кг*м2 также можно записать, как м2*кг. Такая форма записи тоже допускается, однако, в практической физике ее не используют.
Поскольку и килограмм, и метр являются системными единицами измерения массы и длины, соответственно, то кг*м2 является также единицей СИ для момента инерции.
Не следует изучаемую единицу путать с другой, которая обозначается, как кг/м2. Хотя ее используют редко, и она не является единицей СИ, тем не менее она позволяет рассчитать соответствующее давление, если ее умножить на ускорение свободного падения.
Пример задачи
Разобравшись, в чем измеряется момент инерции, и как его вычислять, решим следующую задачу: необходимо определить момент инерции Земли, полагая ее материальной точкой.
Для успешного решения этой задачи следует знать всего два параметра: массу планеты и средний радиус ее солнечной орбиты. Оба значения можно посмотреть в соответствующих справочниках. Масса M и радиус орбиты R Земли равны:
Воспользовавшись выражением для вычисления инерции момента точки материальной, приходим к следующему результату:
I = M*R2 = 5,972*1024*(149,6*109)2 = 1,34*1047 кг*м2.
Мы получили гигантское значение. Если сравнить его с моментом инерции Земли относительно ее собственной оси, то окажется, что он будет в миллиард раз меньше рассчитанной величины. Таким образом, приближение материальной точки вполне уместно для рассмотренной задачи.
Момент инерции для чайников: определение, формулы, примеры решения задач
Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Что такое инерция
Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.
Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».
Определение момента инерции
Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.
По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.
Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.
Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.
Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:
Теорема Штейнера
От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.
Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Теорема Гюйгенса-Штейнера гласит:
Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.
Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:
Пример решения задачи на нахождение момента инерции
Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.
Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.
Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:
Массу кольца можно представить в виде:
Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:
В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.
Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.
Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:
Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.
Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.
Момент инерции сечения
Меня часто спрашивают: «…а что такое моменты инерции в сопротивлении материалов и зачем они вообще?» Об этом в сегодняшней теме
Моменты инерции сечения из простых фигур
Начнем с моментов инерции простых фигур и на их примере выясним для сложных и составных сечений.
Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?
Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?
Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур
Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.
Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:

на балке изображены главные центральные оси z y
прогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.
Вывод моментов инерции для простых фигур
Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.
Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.
Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.
Центральными осями называют оси, которые проходят через центр тяжести сечения
Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции
Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.
При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.
Моменты инерции для прямоугольника
#Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.
Сопротивление материалов и Моменты инерции для прямоугольника. Понятие моментов инерции, формулы и вывод для прямоугольника. Осевые центробежный моменты инерции. для треугольника вывод моментов инерции в этом видео: https://www.youtube.com/embed/_pixohVoc-4?vq=hd720 Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
моменты инерции для прямоугольника для главных центральных осей равны, формула
моменты инерции для прямоугольника для осей проходящих через основные размеры равны, формула
Моменты инерции для треугольника
Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции
Сопротивление материалов и Моменты инерции для треугольника. Сопромат вывод моментов инерции для простых фигур. Моменты инерции для треугольника. Моменты инерции для осей в треугольнике, которые проходят через основные размеры. Вывод и пояснение к этой теме сопротивления материалов. для прямоугольника вывод моментов инерции в этом видео: https://www.youtube.com/watch?v=v1TE1UW_sRE&feature=youtu.be Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2018-04-09
Моменты инерции треугольника относительно произвольых осей

Момент инерции круга. Моменты инерции простых фигур. #сопромат
Вывод моментов инерции для круга. Видео урок из темы «Моменты инерции простых фигур». В видео приведен вывод момента инерции полярного, в полярной системе координат Ip Затем выведены моменты инерции осевые Iz, Iy. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Моменты инерции. Оси центральные и главные. Что это и где. #сопромат
Центральные оси — любая пара взаимно перпендикулярных осей, которые проходят через центр тяжести фигуры Главные оси — оси для которых центробежный момент инерции равен нулю, а осевые моменты имеют максимум и минимум. Об этом и многом другом в видео уроке по моментам инерции в сопротивлении материалов Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline
2019-09-14
Моменты инерции плоских фигур





Моменты инерции плоских фигур
систему осей z и y, перпендикулярных друг другу, провести через полюса, то P2= = z2+Y2-из Формулы (2.7), Jp=Y(Y2h-z2) dF=Y2df+ F F F +Дж з ш-в J2+дя. (2.8) обратите внимание, что величина момента инерции всегда положительна. Центробежным моментом инерции называют Интеграл произведения площади базовой площадки на расстояние от координатных осей z и y: Jzy=jzydf. Райс, четырнадцать. В зависимости от положения оси, момент инерции может быть положительным или отрицательным и может быть равен нулю.
На практике центробежный момент инерции участка фигуры показан на рисунке. 14, а для системы выбранной оси Людмила Фирмаль
положительна, так как z-координата всех элементов положительна. Когда ось вокруг начала координат повернута на 90°(рис. 14, б) знак центробежного момента фигуры изменяется, наоборот, потому что в этом положении z-координата всех элементов положительна, а y-координата отрицательна. 16 очевидно, что если поворачивать ось постепенно, то можно найти положение, в котором центробежная сила будет равна нулю. Такая ОСН называется главной осью инерции. Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры, всегда будут ее главной осью
инерции, поскольку в этом случае каждое положительное значение zy dF равно 14 С на всей площади другой фигуры оси симметрии)и их сумма равна нулю. Главная ось, проходящая через центр тяжести секции, называется главной центральной осью. Момент инерции измеряется в единицах длины четвертого порядка (например, см4). Пятнадцать риса Вычислите момент инерции параллельно его стороне относительно центральной оси G, y(рис. 15). Чтобы определить момент инерции относительно оси Z, выделите основную область узкого прямоугольника, параллельного оси Z. Ширина,
. Тогда Jz=. Предположим, что P=l, a=0, найдем момент инерции полукруга: г Людмила Фирмаль
_YAG* Вычислите момент инерции e l l и N C A semianes a, b (рис. 20) относительно центральной оси Z. Если рассматривать овал как проекцию наклонного круга, то задачу можно решить довольно просто. В то же время V_A Ви А9 Теперь представим себе момент инерции эллипса как сумму момента инерции основного прямоугольника высоты y и ширины dz: Последнее интегрирование справа — это момент инерции окружности с радиусом a относительно оси Z.. b3nab4 связали t? 4-4— * (2L7) Очевидно.,
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Моменты инерции плоских фигур основные понятия




Моменты инерции плоских фигур основные понятия
меньше напряжение и удлинение стержня. Рис 150А Когда сила прикладывается к стержню перпендикулярно его оси, изображение резко меняется. Таким образом, когда стержень, имеющий удлиненное прямоугольное поперечное сечение, закрывается
на одном конце силой, приложенной к другому концу, стержень Людмила Фирмаль
изгибается, и нижняя часть нагрузки имеет определенное значение / 1150, а). Если стержень 168 повернут на 90 ° вокруг оси так, чтобы максимальный размер поперечного сечения был горизонтальным, конец стержня будет иметь значение / 2 с той же нормальной силой. 150, б), намного больше, чем фи. Таким образом, в одной и той же области, в зависимости от ориентации поперечного сечения,
стержень по-разному сопротивляется силам. Следовательно, можно сделать вывод, что площадь поперечного сечения не может характеризовать сопротивление стержня изгибу. При изучении других случаев изгиба, скручивания и деформации стержня было обнаружено, что необходимо включить более сложные геометрические свойства сечения. В связи с этим возникают
координаты центра тяжести графической области определяются по следующей формуле: * Интегральный значок f указывает, что интеграл охватывает всю область диаграммы. 169u *
R • И поэтому S2 = uok5U = z0F. Из последнего уравнения видно, что статический момент фигуры вокруг оси, проходящей через центр тяжести этой фигуры, равен нулю. Ось координат, которая проходит через центр тяжести диаграммы, называется центральной осью. Следующее удовлетворяет геометрическим свойствам в расчете, где элементы области dF умножаются на квадрат расстояния до оси: Jy = J z4F.
Эти значения называются осевыми моментами инерции. Построен интеграл, в котором площадь df умножается на произведение Людмила Фирмаль
координат, и получается центробежный момент инерции Jzy = Jzydf. F Обратите внимание на другое свойство, где подынтегральное выражение является произведением элемента площади dF на квадрат расстояния до начала координат:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института