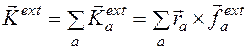в чем измеряется момент импульса
Момент импульса
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.
Момент импульса замкнутой системы сохраняется.
Содержание
Момент импульса в классической механике [ править | править код ]
Определение [ править | править код ]
\mathbf
, где r
\mathbf r — радиус-вектор частицы относительно выбранного начала отсчёта, p
\mathbf p — импульс частицы.
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение:
Вычисление момента [ править | править код ]
Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам r
\theta_
\mathbf p производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения. Направление поворота важно при вычислении, так как определяет знак искомой проекции.
\mathbf r в виде r = r ∥ + r ⊥
\mathbf
\mathbf
\mathbf
\mathbf
I — момент инерции относительно оси вращения, ω
В общем случае вектор момента связан с вектором угловой скорости линейным оператором момента инерции: L = I ^ ω \mathbf
Сохранение углового момента [ править | править код ]
Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем.
\tau_
Математически закон сохранения момента импульса следует из изотропии пространства, то есть из инвариантности пространства по отношению к повороту на произвольный угол. При повороте на произвольный бесконечно малый угол δ φ
i изменятся на δ r i = δ φ × r i
\mathcal L системы при таком повороте не изменится, вследствие изотропии пространства. Поэтому
\mathbf p_i — обобщенный импульс i
Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:
Момент импульса в электродинамике [ править | править код ]
При описании движения заряженной частицы в электромагнитном поле, канонический импульс p
p не является инвариантным. Как следствие, канонический момент импульса L = r × p
\mathbf
-\frac
Момент импульса в квантовой механике [ править | править код ]
Оператор момента [ править | править код ]
В классическом определении момент импульса зависит от 6 переменных r x
Математически, момент импульса в квантовой механике определяется как количество движения — не количественно, а как оператор физической величины: Missing argument for \mathbf \hat\mathbf
,
Симметрия вращения [ править | править код ]
Вычисление момента импульса [ править | править код ]
Если имеется материальная точка массой m
\mathbf
\mathbf
\mathbf
Момент импульса
Ошибка скрипта: Модуля «Infobox» не существует. Шаблон:Карточка/внизу Ошибка скрипта: Модуля «Transclude» не существует.
| Шаблон:Карточка/название | |
|---|---|
| Шаблон:Wikidata |
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Пожалуй, наибольшую роль момент импульса играет при описании собственно вращательного движения. Однако он крайне важен и для гораздо более широкого класса задач (особенно, если в задаче есть центральная или осевая симметрия — но и не только в этих случаях).
Момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.
Момент импульса замкнутой системы сохраняется. Момент импульса является одним из трёх аддитивных (энергия, импульс, момент импульса) интегралов движения.
Содержание
Момент импульса в классической механике
Определение
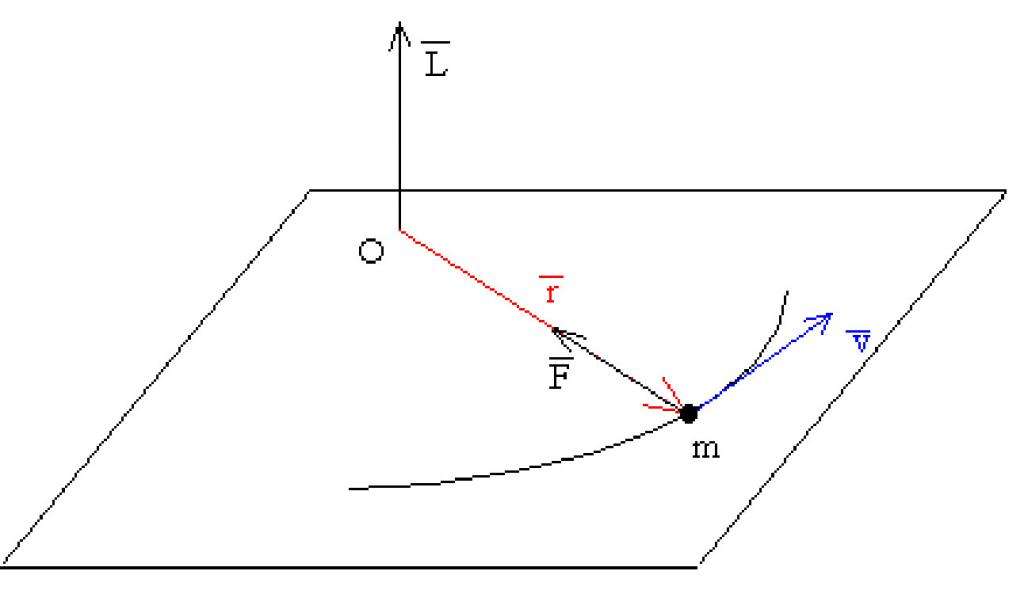
Момент импульса \mathbf L материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
где \mathbf r — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, \mathbf p — импульс частицы.
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
где \mathbf r_i, \mathbf p_i — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как \mathbf
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:
Вычисление момента
\mathbf
= (\mathbf
= \mathbf
+ \mathbf
= \mathbf
. \mathbf
= \mathbf
Сохранение момента импульса
Шаблон:Симметрия в физике Закон сохранения момента импульса (закон сохранения углового момента): векторная сумма всех моментов импульса относительно любой неподвижной точки (или сумма моментов относительно любой неподвижной оси) для замкнутой системы остается постоянной со временем.
Производная момента импульса по времени есть момент силы:
Таким образом, требование замкнутости системы может быть ослаблено до требования равенства нулю главного (суммарного) момента внешних сил:
где \tau_ <\rm ext>— момент одной из сил, приложенных к системе частиц. (Но конечно, если внешние силы вообще отсутствуют, это требование также выполняется).
\dot <\mathbf p_i>\,\delta \varphi \times \mathbf r_i + \mathbf p_i\,\delta \varphi \times \mathbf <\dot r_i>.
Теперь, пользуясь свойством смешанного произведения, совершим циклическую перестановку векторов, в результате чего получим, вынося общий множитель:
\delta \mathcal L = \delta \varphi \sum \limits_i \left( \mathbf r_i \times \dot <\mathbf p_i>+ \dot <\mathbf r_i>\times \mathbf p_i \right) = \delta \varphi \frac
На орбите момент импульса распределяется между моментами импульса собственного вращения планеты и её орбитального движения:
Импульс момента силы
От момента импульса нужно отличать импульс момента силы. Во вращательном движении момент силы, действуя в течение определённого времени, создаёт импульс момента силы (единица измерения — Н·м·с). Импульс момента силы — это мера воздействия момента силы относительно данной оси за данный промежуток времени (во вращательном движении):
\mathbf
Момент импульса в электродинамике
При описании движения заряженной частицы в электромагнитном поле канонический импульс p не является инвариантным. Как следствие, канонический момент импульса \mathbf
тоже не инвариантен. Тогда берем реальный импульс, который также называется «кинетическим импульсом»:
\mathbf
-\frac
где e — электрический заряд, c — скорость света, A — векторный потенциал. Таким образом, гамильтониан (инвариантный) заряженной частицы массы m в электромагнитном поле:
где \varphi — скалярный потенциал. Из этого потенциала следует закон Лоренца. Инвариантный момент импульса, или «кинетический момент импульса», определяется следующим образом:
K= \mathbf
-\frac
Момент импульса в квантовой механике
Оператор момента
Математически полный момент импульса в квантовой механике определяется как оператор физической величины из суммы двух частей, связанных с пространственным движением — в атомной физике такой момент называют орбитальным, и внутренним спином частицы — соответственно, спиновым. Первый оператор действует на пространственные зависимости волновой функции:
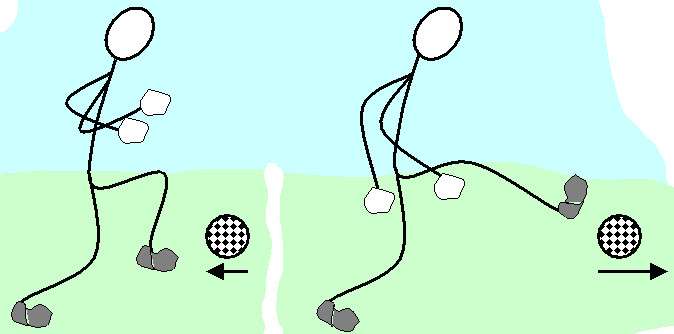
где \hat<\mathbf > — координатный и импульсный оператор, соответственно, а второй — на внутренние, спиновые. В частности, для одной частицы без электрического заряда и без спина, оператор углового момента может быть записан как: где \nabla — оператор набла. Это часто встречающаяся форма оператора момента импульса, но не самая главная, она имеет следующие свойства: [L_i,\; L_j ] = i \hbar \varepsilon_ и даже более важные подстановки с гамильтонианом частицы без заряда и спина: \left[L_i,\; H \right] = 0. Операторы момента импульса обычно встречаются при решении задач сферической симметрии в сферических координатах. Тогда момент импульса в пространственном отображении: Когда находят собственные значения этого оператора, получают следующее: L^2 \mid l,\; m \rang = <\hbar>^2 l(l+1) \mid l,\; m \rang, L_z \mid l,\; m \rang = \hbar m \mid l,\; m \rang, \mathbf Чтобы рассчитать момент импульса тела, его надо разбить на бесконечно малые кусочки и векторно просуммировать их моменты как моменты импульса материальных точек, то есть взять интеграл: Можно переписать это через плотность \rho : (Если считать, что \rho(x,y,z) — обобщенная функция, включающая, возможно, и дельтообразные члены, то последняя формула применима и к распределенным, и к дискретным системам). Для систем, совершающих вращение как целое (как абсолютно твёрдое тело) вокруг одной из осей симметрии (или, в более общем виде — вокруг так называемых главных осей инерции тела), справедливо соотношение где I — момент инерции относительно оси вращения, \boldsymbol\omega — вектор угловой скорости. В общем случае вектор момента связан с вектором угловой скорости через линейный оператор момента инерции (тензор инерции): Моме?нт и?мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Момент импульса материальной точки относительно точки O определяется векторным произведением Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса): Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело: Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени. Аналогично для замкнутой системы тел, вращающихся вокруг оси z: Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения. Закон сохранения момента импульса вытекает из основного уравнения динамики вращательного движения тела, закрепленного в неподвижной точке (уравнение 4.8), и состоит в следующем: — если результирующий момент внешних сил относительно неподвижной точки тождественно равен нулю, то момент импульса тела относительно этой точки с течением времени не изменяется. Другими словами, момент импульса замкнутой системы с течением времени не изменяется. — если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения, т.е. если Mz = 0, то dLz / dt = 0, откуда Закон сохранения момента импульса является фундаментальным законом природы. Справедливость этого закона обусловливается свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета. Умножая уравнение (1.7) слева векторно на радиус-вектор Где вектор Несколько тел, каждое из которых можно рассматривать как материальную точку, составляют Систему материальных точек. Для каждой материальной точки можно записать уравнение второго закона Ньютона В уравнении (1.13) индексы Из уравнений (1.13) вытекают несколько важных законов. Если просуммируем их по всем материальным точкам системы, то получим Величина Называется Импульсом системы материальных точек. Импульс системы материальных точек равен сумме импульсов отдельных материальных точек. В уравнении (1.14) двойная сумма для внутренних сил обращается в нуль. Для каждой пары материальных точек в нее входят силы, которые по третьему закону Ньютона равны и противоположно направлены. Для каждой пары векторная сумма этих сил обращается в нуль. Поэтому равна нулю и сумма для всех сил. В результате получим: Уравнение (1.16) выражает закон изменения импульса системы материальных точек. Изменение импульса системы материальных точек вызывается только внешними силами. Если на систему не действуют внешние силы, то импульс системы материальных точек сохраняется. Систему материальных точек, на которую не действуют внешние силы, называют Изолированной, или замкнутой, системой материальных точек. Аналогичным образом для каждой материальной точки записываются уравнения (1.8) моментов импульсов При суммировании уравнений (1.17) по всем материальным точкам системы материальных точек сумма моментов внутренних сил обращается в нуль и получается Закон изменения момента импульса системы материальных точек: Где введены обозначения: Задачи с движущимися телами в физике, когда скорость много меньше световой, решаются с помощью законов ньютоновской, или классической механики. В ней одним из важных понятий является импульс. Основные формулы импульса в физике приводятся в данной статье. Под количеством движения понимают произведение скорости перемещения тела на инерционный коэффициент, то есть на массу. Соответствующая формула имеет вид: Понятие о количестве движения в настоящее время используют реже, чем об импульсе. И связан этот факт непосредственно с законами ньютоновской механики. Запишем его в форме, которая приводится в школьных учебниках по физике: Заменим ускорение a¯ на соответствующее выражение с производной скорости, получим: Перенося dt из знаменателя правой части равенства в числитель левой, получаем: Мы получили интересный результат: помимо того, что действующая сила F¯ приводит к ускорению тела (см. первую формулу этого пункта), она также изменяет количество его движения. Произведение силы на время, которое стоит в левой части, называется импульсом силы. Он оказывается равным изменению величины p¯. Поэтому последнее выражение называют также формулой импульса в физике. Формулы в физике, которые описывают сохранение величины p¯, могут быть приведены в нескольких вариантах. Прежде чем их записывать, ответим на вопрос о том, когда сохраняется импульс. Обратимся к выражению из предыдущего пункта: Оно говорит о том, что если сумма внешних сил, оказывающих воздействие на систему, равна нулю (закрытая система, F¯= 0), тогда dp¯= 0, то есть никакого изменения количества движения не будет происходить: Это выражение является общим для импульса тела и закона сохранения импульса в физике. Отметим два важных момента, о которых следует знать, чтобы с успехом применять это выражение на практике: Частным случаем использования формулы импульса в физике и его сохранения является движение двух тел, которые сталкиваются друг с другом. Рассмотрим два принципиально разных случая, о которых упоминалось в пункте выше. m1*v1 + m2*v2 = m1*u1 + m2*u2 Здесь важно помнить, что знак скорости должен подставляться с учетом ее направления вдоль рассматриваемой оси (противоположные скорости имеют разные знаки). Эта формула показывает, что при условии известного начального состояния системы (величины m1, v1, m2, v2) в конечном состоянии (после столкновения) имеется две неизвестных (u1, u2). Найти их можно, если воспользоваться соответствующим законом сохранения кинетической энергии: m1*v12 + m2*v22 = m1*u12 + m2*u22 m1*v1 + m2*v2 = (m1 + m2)*u Как видно, речь идет всего об одной неизвестной (u), поэтому для ее определения достаточно этого одного равенства. Все, что было сказано выше об импульсе, относится к линейным перемещениям тел. Как быть в случае вращения объектов вокруг оси? Для этого в физике введено другое понятие, которое аналогично линейному импульсу. Оно называется моментом импульса. Формула в физике для него принимает следующий вид: Формула для L¯, которая приведена выше, является определением этой величины. На практике же предпочитают использовать несколько иное выражение. Не будем вдаваться в подробности его получения (это несложно, и каждый может проделать это самостоятельно), а приведем его сразу: Если на вращающую систему не действуют никакие внешние силы (в действительности момент сил), то произведение I на ω¯ будет сохраняться независимо от процессов, происходящих внутри системы. То есть закон сохранения для L¯ имеет вид: Примером его проявления является выступление спортсменов в фигурном катании, когда они совершают вращения на льду.Симметрия вращения
Вычисление момента импульса в нерелятивистской механике
Момент импульса. Момент силы. Закон сохранения момента импульса. Изменение импульса.



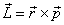
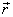
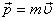
Момент импульса материальной точки относительно неподвижной оси 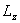
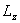
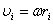
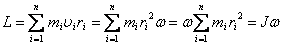
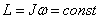
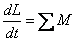
Это один из фундаментальных законов природы.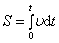
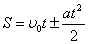
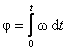
Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.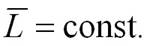
Из основного закона динамики тела, вращающегося вокруг неподвижной оси z (уравнение 4.13), следует закон сохранения момента импульса тела относительно оси: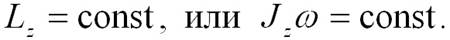
Изменение импульса материальной точки вызывается действием на нее силы.
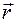
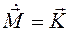
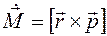
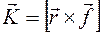
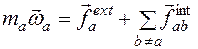
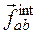
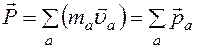
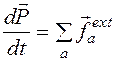
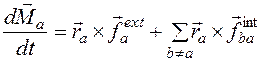
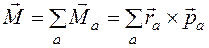
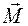
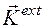
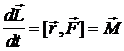
Импульс и момент импульса в физике: формулы, описывающие закон сохранения этих величин
Импульс или количество движения?


Изменение величины p¯
Закон сохранения импульса
Упругое и неупругое взаимодействие двух тел
Импульс тела во время движения по окружности
Закон сохранения L¯