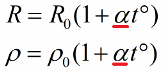в чем измеряется коэффициент сопротивления

Электрическое сопротивление.

Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.

Электрическое сопротивление определяется как коэффициент пропорциональности R между напряжением U и силой постоянного тока I в законе Ома для участка цепи.

Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом (1 Ом) — это сопротивление такого проводника, в котором при напряжении 1 В сила тока равна 1 А.

Удельное сопротивление.

Сопротивление однородного проводника постоянного сечения зависит от материала проводника, его длины l и поперечного сечения S и может быть определено по формуле:

,

Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.

Из формулы следует, что

,

Величина, обратная ρ, называется удельной проводимостью σ:

.

Зависимость сопротивлений от температуры.

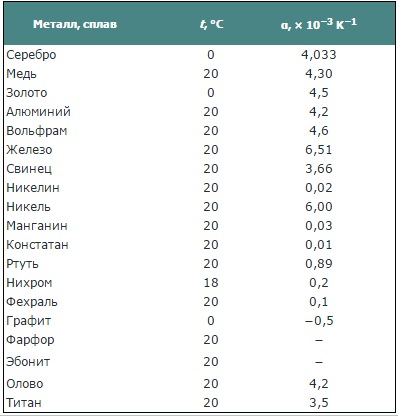
С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.

Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на 1 °С к величине его сопротивления при 0 ºС:

.

Зависимость удельного сопротивления проводников от температуры выражается формулой:

.

Зависимость сопротивления проводника от температуры используется в термометрах сопротивления.

Источник

Температурный коэффициент электрического сопротивления

Из Википедии — свободной энциклопедии

Температу́рный коэффицие́нт электри́ческого сопротивле́ния — величина, равная относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на единицу.

Температурный коэффициент сопротивления характеризует зависимость электрического сопротивления от температуры и измеряется в кельвинах в минус первой степени (K −1 ).

Также часто применяется термин «температурный коэффициент проводимости». Он равен значению коэффициента сопротивления с обратным знаком.

Для большинства металлов температурный коэффициент сопротивления положителен: их сопротивление растёт с ростом температуры вследствие рассеяния электронов на фононах (тепловых колебаниях кристаллической решётки).

Для полупроводников без примесей он отрицателен (сопротивление с ростом температуры падает), поскольку при повышении температуры всё большее число электронов переходит в зону проводимости, соответственно увеличивается и концентрация дырок. Качественно такой же характер (и по тем же причинам) имеет температурная зависимость сопротивления твёрдых и неполярных жидких диэлектриков. Полярные жидкости уменьшают своё удельное сопротивление с ростом температуры более резко вследствие роста степени диссоциации и уменьшения вязкости. На практике этот эффект применялся для защиты электронных ламп от пусковых токов (см. Урдокс).

Температурная зависимость сопротивления металлических сплавов, газов, легированных полупроводников и электролитов носит более сложный характер.

Существуют сплавы (константан, манганин), имеющие очень малый температурный коэффициент сопротивления, то есть их сопротивление очень слабо зависит от температуры. Эти сплавы применяются в электроизмерительной аппаратуре.

Источник

Гидравлическое сопротивление

Гидравлическое сопротивление или гидравлические потери – это суммарные потери при движении жидкости по водопроводящим каналам. Их условно можно разделить на две категории:

Потери трения – возникают при движении жидкости в трубах, каналах или проточной части насоса.

Потери на вихреобразование – возникают при обтекании потоком жидкости различных элементов. Например, внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п. Такие потери принято называть местными гидравлическими сопротивлениями.

Содержание статьи

Коэффициент гидравлического сопротивления

Гидравлические потери выражают либо в потерях напора Δh в линейных единицах столба среды, либо в единицах давления ΔP:

где ρ — плотность среды, g — ускорение свободного падения.

В производственной практике перемещение жидкости в потоках связано с необходимостью преодолеть гидравлическое сопротивление трубы по длине потока, а также различные местные сопротивления:
Поворотов
Диафрагм
Задвижек
Вентилей
Кранов
Различных ответвлений и тому подобного

На преодоление местных сопротивлений затрачивается определенная часть энергии потока, которую часто называют потерей напора на местные сопротивления. Обычно эти потери выражают в долях скоростного напора, соответствующего средней скорости жидкости в трубопроводе до или после местного сопротивления.

Аналитически потери напора на местные гидравлические сопротивления выражаются в виде.

где ξ – коэффициент местного сопротивления (обычно определяется опытным путем).

Данные о значении коэффициентов различных местных сопротивлений приводятся в соответствующих справочниках, учебниках и различных пособиях по гидравлике в виде отдельных значений коэффициента гидравлического сопротивления, таблиц, эмпирических формул, диаграмм и т.д.

Исследование потерь энергии (потери напора насоса), обусловленных различными местными сопротивлениями, ведутся уже более ста лет. В результате экспериментальных исследований, проведенных в России и за рубежом в различное время, получено огромное количество данных, относящихся к разнообразнейшим местным сопротивлениям для конкретных задач. Что же касается теоретических исследований, то им пока поддаются только некоторые местные сопротивления.

В этой статье будут рассмотрены некоторые характерные местные сопротивления, часто встречающиеся на практике.

Местные гидравлические сопротивления

Как уже было написано выше, потери напора во многих случаях определяются опытным путем. При этом любое местное сопротивление похоже на сопротивление при внезапном расширении струи. Для этого имеется достаточно оснований, если учесть, что поведение потока в момент преодоления им любого местного сопротивления связано с расширением или сужением сечения.

Гидравлические потери на внезапное сужение трубы

Сопротивление при внезапном сужении трубы сопровождается образованием в месте сужения водоворотной области и уменьшения струи до размеров меньших, чем сечение малой трубы. Пройдя участок сужения, струя расширяется до размеров внутреннего сечения трубопровода. Значение коэффициента местного сопротивления при внезапном сужении трубы можно определить по формуле.

Значение коэффициента ξ_{вн. суж} от значения отношения (F₂/F₁)) можно найти в соответствующем справочнике по гидравлике.

Гидравлические потери при изменении направления трубопровода под некоторым углом

В этом случае вначале происходит сжатие, а затем расширение струи вследствие того, что в месте поворота поток по инерции как бы отжимается от стенок трубопровода. Коэффициент местного сопротивления в этом случае определяется по справочным таблицам или по формуле

ξ _{поворот} = 0,946sin(α/2) + 2.047sin(α/2) 2

где α – угол поворота трубопровода.

Местные гидравлические сопротивления при входе в трубу

В частном случае вход в трубу может иметь острую или закругленную кромку входа. Труба, в которую входит жидкость, может быть расположена под некоторым углом α к горизонтали. Наконец, в сечении входа может стоять диафрагма, сужающая сечение. Но для всех этих случаев характерно начальное сжатие струи, а затем её расширение. Таким образом и местное сопротивление при входе в трубу может быть сведено к внезапному расширению струи.

Если жидкость входит в цилиндрическую трубу с острой кромкой входа и труба наклонена к горизонту под углом α, то величину коэффициента местного сопротивления можно определить по формуле Вейсбаха:

ξ_вх = 0,505 + 0,303sin α + 0,223 sin α 2

Местные гидравлические сопротивления задвижки

На практике часто встречается задача расчета местных сопротивлений, создаваемых запорной арматурой, например, задвижками, вентилями, дросселями, кранами, клапанами и т.д. В этих случаях проточная часть, образуемая разными запорными приспособлениями, может иметь совершенно различные геометрические формы, но гидравлическая сущность течения при преодолении этих сопротивлений одинакова.

Гидравлическое сопротивление полностью открытой запорной арматуры равно

ξ_{вентиля} = от 2,9 до 4,5

Величины коэффициентов местных гидравлических сопротивлений для каждого вида запорной арматуры можно определить по справочникам.

Гидравлические потери диафрагмы

Процессы, происходящие в запорных устройствах, во многом похожи на процессы при истечении жидкости через диафрагмы, установленные в трубе. В этом случае также происходит сужение струи и последующее её расширение. Степень сужения и расширения струи зависит от ряда условий:
режима движения жидкости
отношения диаметров отверстия диафрагмы и трубы
конструктивных особенностей диафрагмы.

Для диафрагмы с острыми краями:

Местные гидравлические сопротивления при входе струи под уровень жидкости

Преодоление местного сопротивления при входе струи под уровень жидкости в достаточно большой резервуар или в среду, не заполненную жидкостью, связано с потерей кинетической энергии. Следовательно, коэффициент сопротивления в этом случае равен единице.

Видео о гидравлическом сопротивлении

На преодоление гидравлических потерь затрачивается работа различных устройств (насосов и гидравлических машин)

Для снижения влияния гидравлических потерь рекомендуется в конструкции трассы избегать использования узлов способствующих резким изменениям направления потока и стараться применять в конструкции тела обтекаемой формы.

Даже применяя абсолютно гладкие трубы приходится сталкиваться с потерями: при ламинарном режиме течения(по Рейнольдсу) шероховатость стенок не оказывает большого влияния, но при переходе к турбулентному режиму течения как правило возрастает и гидравлическое сопротивление трубы.

Источник

В чем измеряется температурный коэффициент сопротивления

Температурный коэффициент сопротивления резистора

Так как под воздействием температуры окружающей среды или из-за нагрева самого резистора удельное сопротивление его резистивного слоя может меняться, то для обозначения термостабильности резисторов ввели такое понятие, как температурный коэффициент сопротивления (ТКС).

В зарубежной документации он именуется, как TCR (Temperature Coefficient of Resistance).

ТКС показывает насколько меняется сопротивление резистора при изменении температуры на 1°С или 1° Кельвина. Так как температура может меняться в большую или меньшую сторону, то указывается знак «±». Начальной температурой считается +25°С (комнатная), если другое значение не оговаривается отдельно.

Формула расчёта ТКС.

TCR – температурный коэффициент сопротивления (ТКС), (ppm/°С);

R₁ – сопротивление при комнатной температуре +25°С, (Ω);

R₂ – сопротивление при рабочей температуре, (Ω);

T₁ – комнатная температура (+25°С);

T₂ – рабочая температура при которой производится тестовое измерение, (°С).

Данную формулу также нередко записывают и в сокращённом виде:

В технической документации на импортные резисторы температурный коэффициент может указываться как в градусах (± ppm/°С), так и в Кельвинах (± ppm/K). Это одно и то же.

Чтобы представить, что же такое ppm/°С в более наглядном виде, приведу пример.

Допустим, что у нас имеется резистор сопротивлением 1000000 Ω (один миллион Ом, или МегаОм – 1 МОм). Мы знаем, что его температурный коэффициент равен ±25 ppm/°С. Так как 25 – это количество частей от одного миллиона, то получаем 25/1000000 = 0,000025. Умножаем 0,000025 на 1000000 (номинал нашего резистора), чтобы узнать, каково же будет изменение в Омах. Получаем 25. То есть это всего 25 Ом от нашего мегаомного резистора. Именно на такую величину изменится сопротивление нашего резистора, если температура поднимется на 1°С. Тогда его результирующее сопротивление составит 1000000 (Ω) + 25 (Ω) = 1000025 (Ω).

Обращаю внимание на то, что ppm не имеет размерности. Тут речь идёт именно о долях от чего либо, в данном случае миллиона!

В процентах это будет 0,000025 × 100% = 0,0025%. То есть сопротивление резистора изменится на 0,0025% по отношению к первоначальному (1 Мом).

Другой пример, более приближённый к практике.

Имеется резистор на 56 килоОм (56 000 Ом). Его температурный коэффициент составляет ±50 ppm/°С. Давайте рассчитаем, в каких пределах будет меняться его сопротивление при изменении температуры на ±10°С. То есть при охлаждении на 10°С, так и нагреве на 10°С. Диапазон изменения температуры в данном случае составит 20°С.

Как уже говорилось, стартовой температурой отсчёта считается +25°С. Именно при такой температуре наш резистор имеет сопротивление 56 кОм.

Сначала узнаем, насколько изменится сопротивление нашего резистора при изменении температуры на 1°С. Считать будем по следующей формуле. Наверняка уже заметили, что это та же самая формула расчёта ТКС, только изменённая.

ΔR – величина, на которое изменится сопротивление (в Омах, Ω);

R – сопротивление резистора при +25°С (комнатная температура);

ΔT – изменение температуры, °С. В нашем случае, это 1°С.

Таким образом мы узнали, что при изменении температуры на 1 градус, сопротивление нашего резистора изменится на 2,8 Ом. Соответственно, при изменении температуры на 10°С, сопротивление изменится на 28 Ом. В результате получаем диапазон изменения сопротивления от 55972 Ом (при 15°С) до 56 028 Ом (при 35°С). Как видим, наш резистор имеет очень хорошую термостабильность. Его сопротивление меняется незначительно, особенно, если учесть тот факт, что среди резисторов много и таких, у которых ТКС равен 100. 300 ppm/°С.

Как пример, далее показан график, взятый из даташита на серию резисторов VSMP от Vishay. На нём показаны значения T.C.R для разных температурных диапазонов.

+600 ppm/°С. Это означает, что при понижении температуры резистор ведёт себя более стабильней, и его сопротивление изменяется меньше, чем при её повышении.

Можно заметить и то, что для конкретного диапазона сопротивлений указывается своя величина T.C.R.

Величина ТКС не указывается в маркировке резисторов. Узнать его можно из технической документации на конкретную серию резисторов. Надо отметить, что ТКС резистора сильно зависит от материала, из которого изготовлен его резистивный слой, а также технологии его производства.

Далее для сравнения приведены величины ТКС для резисторов с разной резистивной основой и технологией производства.

Тип резистора и его температурный коэффициент сопротивления:

Самым большим (и плохим) температурным коэффициентом обладают резисторы с проводящим слоем на основе углерода. Их ТКС может достигать 5000 ppm/°С! Резисторы на основе углеродной проводящей плёнки (carbon film resistors) имеют ТКС в диапазоне 200. 500 ppm/°С (CF-25, CF-100 и им подобные). Именно поэтому допуск (точность) таких резисторов редко меньше 5%.

Металлоплёночные (серия MF, например, MF-100). Их TCR обычно лежит в диапазоне ±15. 100 ppm/°С, но в некоторых случаях вплоть до 10 ppm/°С. На фото – металлоплёночные прецизионные резисторы серии RN (Military). Нашёл их на печатной плате от промышленного станка. ТКС резистора RN55E – 25 ppm/°С, а RN55D – 100 ppm/°С.

Металлооксидные плёночные резисторы (серия MO, например, MO-200) имеют ТКС в диапазоне 100. 200 ppm/°С.

На фото показаны металлооксидные (металлодиэлектрические) резисторы МО-200 (160Ω, 5%). Их ТКС равен 200 ppm/°С;

Толстоплёночные чип-резисторы (T.C.R составляет 50. 200 ppm/°С, реже 300 ppm/°С);

Тонкоплёночные чип-резисторы (ТКС составляет 5. 50 ppm/°С). Это одни из самых термостабильных резисторов. Малым ТКС обладают тонкоплёночные прецизионные резисторы. Он может составлять всего ±2–5 ppm/°С. В документации на такие резисторы можно встретить обозначение Low TCR – низкий ТКС;

Самым малым ТКС обладают фольговые резисторы (Bulk Metal ® Foil, BMF). Это самые термостабильные из всех существующих резисторов. Например, ультрамалый ТКС (всего 0,05 ppm/°С) имеют прецизионные фольговые резисторы серии VSMP Vishay (сверхточные фольговые резисторы для поверхностного монтажа).

Стоит отметить, что величина ТКС очень сильно влияет на тот самый допуск (или точность) резистора, которую указывают в процентах и кодируют в его маркировке (0,5%, 1%, 2%, 5%).

Напомню, что допуск указывает на разброс реального сопротивления резистора, который образуется из-за многих факторов, например, из-за погрешности технологии производства. Сюда же входит и разброс сопротивления из-за наличия ТКС. Именно поэтому, у резисторов с плохой термостабильностью (например, углеродистых) допуск также очень большой, так как при массовом производстве очень трудно сделать его меньше 2. 5%.

Аналогичная ситуация обстоит и с толстоплёночными SMD-резисторами. В составе резистивной пасты, которая используется для формирования проводящего слоя, присутствует серебро, из-за которого ТКС таких резисторов, как правило, не менее 50 ppm/°С.

Электрическое сопротивление проводника в общем случае зависит от материала проводника, от его длины и от поперечного сечения, или более кратко — от удельного сопротивления и от геометрических размеров проводника. Данная зависимость общеизвестна и выражается формулой:

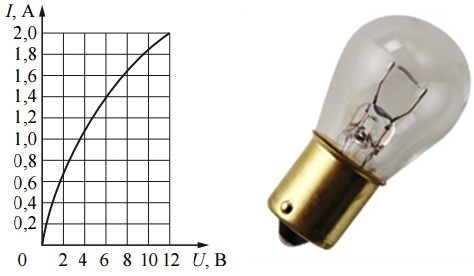
Известен каждому и закон Ома для однородного участка электрической цепи, из которого видно, что ток тем меньше, чем сопротивление выше. Таким образом, если сопротивление проводника постоянно, то с ростом приложенного напряжения ток должен бы линейно расти. Но в реальности это не так. Сопротивление проводников не постоянно.

За примерами далеко ходить не надо. Если к регулируемому блоку питания (с вольтметром и амперметром) подключить лампочку, и постепенно повышать напряжение на ней, доводя до номинала, то легко заметить, что ток растет не линейно: с приближением напряжения к номиналу лампы, ток через ее спираль растет все медленнее, причем лампочка светится все ярче.

Нет такого, что с увеличением вдвое приложенного к спирали напряжения, вдвое возрос и ток. Закон Ома как-будто не выполняется. На самом деле закон Ома выполняется, и точно, просто сопротивление нити накала лампы непостоянно, оно зависит температуры.

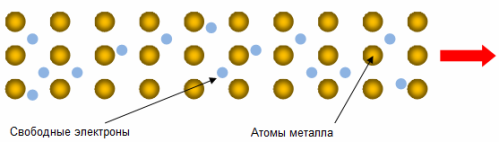
Вспомним, с чем связана высокая электрическая проводимость металлов. Она связана с наличием в металлах большого количества носителей заряда — составных частей тока — электронов проводимости. Это электроны, образующиеся из валентных электронов атомов металла, которые для всего проводника являются общими, они не принадлежат каждый отдельному атому.

Под действием приложенного к проводнику электрического поля, свободные электроны проводимости переходят из хаотичного в более-менее упорядоченное движение — образуется электрический ток. Но электроны на своем пути встречают препятствия, неоднородности ионной решетки, такие как дефекты решетки, неоднородная структура, вызванные ее тепловыми колебаниями.

Электроны взаимодействуют с ионами, теряют импульс, их энергия передается ионам решетки, переходит в колебания ионов решетки, и хаос теплового движения самих электронов усиливается, от того проводник и нагревается при прохождении по нему тока.

В диэлектриках, полупроводниках, электролитах, газах, неполярных жидкостях — причина сопротивления может быть иной, однако закон Ома, очевидно, не остается постоянно линейным.

Таким образом, для металлов, рост температуры приводит к еще большему возрастанию тепловых колебаний кристаллической решетки, и сопротивление движению электронов проводимости возрастает. Это видно по эксперименту с лампой: яркость свечения увеличилась, но ток возрос слабее. То есть изменение температуры повлияло на сопротивление нити накаливания лампы.

В итоге становится ясно, что сопротивление металлических проводников зависит почти линейно от температуры. А если принять во внимание, что при нагревании геометрические размеры проводника меняются слабо, то и удельное электрическое сопротивление почти линейно зависит от температуры. Зависимости эти можно выразить формулами:

Данный коэффициент численно равен относительному изменению электрического сопротивления проводника при изменении его температуры на 1К (на один градус Кельвина, что равноценно изменению температуры на один градус Цельсия).

Для металлов ТКС (температурный коэффициент сопротивления α) хоть и относительно мал, но всегда больше нуля, ведь при прохождении тока электроны тем чаще сталкиваются с ионами кристаллической решетки, чем выше температура, то есть чем выше тепловое хаотичное их движение и чем выше их скорость. Сталкиваясь в хаотичном движении с ионами решетки, электроны металла теряют энергию, что мы и видим в результате — сопротивление при нагревании проводника возрастает. Данное явление используется технически в термометрах сопротивления.

Что касается чистых полупроводников, то для них ТКС отрицателен, то есть сопротивление снижается с ростом температуры, это связано с тем, что с ростом температуры все больше электронов переходят в зону проводимости, растет при этом и концентрация дырок. Этот же механизм свойственен для жидких неполярных и твердых диэлектриков.

Полярные жидкости свое сопротивление резко уменьшают с ростом температуры из-за снижения вязкости и роста диссоциации. Это свойство применяется для защиты электронных ламп от разрушительного действия больших пусковых токов.

У сплавов, легированных полупроводников, газов и электролитов тепловая зависимость сопротивления более сложна чем у чистых металлов. Сплавы с очень малым ТКС, такие как манганин и константан, применяют в электроизмерительных приборах.

содержание

Отрицательный температурный коэффициент

Большинство керамика демонстрирует отрицательную температурную зависимость поведения сопротивления. Этот эффект определяется с помощью уравнения Аррениуса в широком диапазоне температур:

р знак равно A ⋅ е В T >>

р знак равно р ∞ е В T знак равно р 0 е – В T 0 е В T е ^ > = R_ е ^ , >>> е ^ >>

Реверсивный температурный коэффициент

р T С знак равно Δ В р В р Δ T × 100
> раз 100>

Электрическое сопротивление

ρ ⁡ ( T ) знак равно ρ 0 [ 1 + α 0 ( T – T 0 ) ] (Т) = Rho _ [1+ альфа _ (Т-Т_ )]>

α 0 знак равно 1 ρ 0 [ δ ρ δ T ] T знак равно T 0 = >> влево [ > вправо] _ >>

ρ ⁡ ( T ) знак равно S α В T (Т) = S альфа ^ >>

Для обоих, называют температурным коэффициентом сопротивления. α

Это свойство используется в таких устройствах, как термисторы.

Положительный температурный коэффициент сопротивления

Отрицательный температурный коэффициент сопротивления

Отрицательный температурный коэффициент сопротивления полупроводника

Повышение температуры полупроводникового материала приводит к увеличению концентрации носителей заряда. Это приводит к увеличению числа носителей заряда, доступных для рекомбинации, увеличение проводимости полупроводника. Повышение проводимости приводит к тому, удельное сопротивление полупроводникового материала уменьшается с ростом температуры, что приводит к отрицательным температурным коэффициентом сопротивления.

Температурный коэффициент упругости

Температурный коэффициент реактивности

α T знак равно ∂ ρ ∂ T = >>

Математический вывод аппроксимации коэффициента температурного

В более общем виде, температура коэффициент дифференциальной закон:

р 0 знак равно р ( T 0 ) = R (Т_ )>

Интегрирование температуры коэффициент дифференциального закона:

р ( T ) знак равно р 0 ( 1 + α ( T – T 0 ) ) (1+ альфа (Т-Т_ ))>

Единицы

Источник