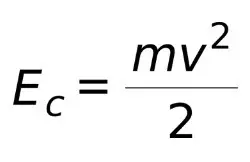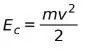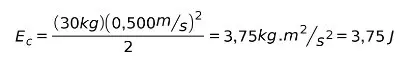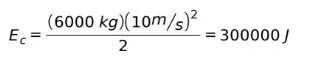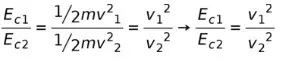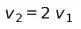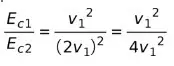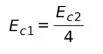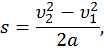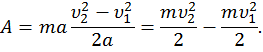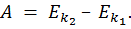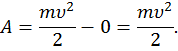в чем измеряется кин энергия

Что такое кинетическая энергия

Кинетическая энергия — это энергия, создаваемая движущимся телом. На греческом языке кинетика означает «движение», в то время как энергия означает «работа». Другими словами, кинетическая энергия — это работа, которую тело выполняет, когда оно движется.

Мы можем воспользоваться кинетической энергией многих природных явлений. Например, движение воды в реке превращается в электричество благодаря электростанциям. Энергия ветра — это кинетическая энергия воздуха. Когда мы прибиваем гвоздь молотком, мы используем кинетическую энергию молотка при его перемещении.

Кинетическая энергия в физике измеряется в джоулях, сокращенно буквой J.

Формула кинетической энергии

Для расчета кинетической энергии тел используется уравнение:

Это означает, что кинетическая энергия Ec равна массе тела m, умноженной на квадрат скорости v, делённые на 2.

Мы можем сделать вывод, что чем больше масса, тем больше энергия, и что энергия пропорциональна скорости, умноженной на себя.

Кинетическая энергия не является вектором. Это означает, что если вы бросаете шар со скоростью 5 м/с, шар будет иметь одинаковую кинетическую энергию, независимо от того, бросаете ли вы его влево или вправо или вверх.

Кинетическая энергия зависит от массы и скорости.

Гоночные машины спроектированы с наименьшей массой для улучшения характеристик.

Кинетическая энергия зависит от массы и скорости тела. Это означает, что чем больше или быстрее объект, тем больше энергии он производит.

Примером вышесказанного может быть следующее: грузовик больше, чем автомобиль; Если оба едут с одинаковой скоростью и врезаются в стену, урон, нанесенный грузовиком, будет больше. В этом случае грузовик обладает большей кинетической энергией.

А теперь представьте: две одинаковые машины едут, одна со скоростью 50 км/ч, а другая со скоростью 100 км/ч. Чем выше скорость, тем серьезнее авария.

Таким образом, кинетическая энергия зависит от квадрата скорости. Это означает, что когда скорость объекта удваивается, его кинетическая энергия увеличивается в четыре раза.

Автомобиль, движущийся со скоростью 60 км/ч, имеет в четыре раза больше кинетической энергии, чем автомобиль, движущийся со скоростью 30 км/ч, и, следовательно, в четыре раза больший потенциал разрушения в случае аварии.

Как рассчитать кинетическую энергию тела?

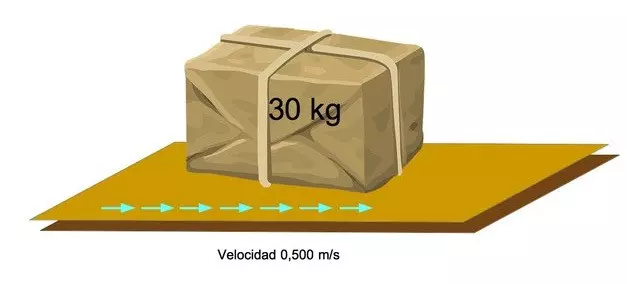
В аэропорту хотят рассчитать кинетическую энергию 30-килограммовой упаковки в системе, которая движется со скоростью 0,500 м/с. Как мы это делаем?

Решение

Мы знаем массу и скорость упаковки, поэтому используем формулу:

Подставляя значения, имеем:

Рассуждение

Единицей кинетической энергии является джоуль, которая является той же для единицы работы. Обратите внимание, что, несмотря на то, что он тяжелый, его кинетическая энергия не так велика из-за его низкой скорости.

Ключевые моменты для запоминания

Задачи на кинетическую энергию и решение

Задача 1 на нахождение кинетической энергии

Слон в 6000 кг бежит со скоростью 10 м/с. Какова его кинетическая энергия? Какова скорость пушечного ядра весом 1 кг, если у него была та же самая кинетическая энергия слона?

Ответ

Используя уравнение кинетической энергии, энергия слона равна:

Рассчитав кинетическую энергию, мы можем получить скорость пули, очистив v:

Это означает, что скорость пули равна 775 м/с. Сравните это со скоростью слона: вот это разница!

Задача 2

Мужчина врезался в столб на своей машине. Когда он пошел, чтобы сообщить о катастрофе, он сказал, что ехал с допустимой скоростью во время аварии. Но следователь помнил физику 7 и 8 класса и установил, что скорость транспортного средства была в два раза выше, чем утверждал водитель. Какова взаимосвязь между кинетической энергией и скоростью, сообщаемой человеком, и кинетической энергией со скоростью, рассчитанной следователем?

Ответ

Мы будем рассматривать Ec1 как кинетическую энергию транспортного средства на скорости v1, сообщаемой человеком, и Ec2 как кинетическую энергию со значением скорости v2, рассчитанным исследователем. Соотношение между кинетическими энергиями рассчитывается путем деления энергий следующим образом:

Следователь сказал, что скорость во время аварии была вдвое выше, чем сообщал человек, то есть:

Подставим значение скорости в уравнение:

Исключая похожие термины, мы имеем:

Это означает, что кинетическая энергия в соответствии со скоростью, сообщаемой человеком, составляет четверть кинетической энергии по расчетам следователя. Проще говоря, ущерб, нанесенный автомобилем, был в четыре раза больше, чем сообщал мужчина.

Источник

Кинетическая энергия.

Кинетическая энергия – энергия движения. Это физическая величина, характеризующая движущееся тело. Кинетической энергией обладает тело и не взаимодействующее с другими телами.

Рассмотрим простейший случай, когда векторы силы и перемещения направлены вдоль одной прямой в одну и ту же сторону. Координатная ось направлена в ту же сторону. Тогда проекции силы, перемещения, ускорения и скорости будут равны модулям самих векторов.

В таком случае работа силы будет равна:

При прямолинейном равноускоренном движении перемещение и скорость связаны соотношением:

где υ₁ и υ₂ – модули векторов скоростей в начале и в конце участка пути, пройденного телом.

Подставив значения F и s в формулу, получим:

В правой части равенства мы получили изменение величины 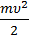— половины произведения массы тела на квадрат его скорости. Эта величина называется кинетической энергией тела, обозначается E_k. В этом случае:

Работа равнодействующей сил, приложенных к телу, равна изменению кинетической энергии тела. Это теорема о кинетической энергии.

Если сила, действующая на тело, направлена в сторону движения, то она совершает положительную работу, т. е. Значит, , кинетическая энергия тела увеличивается. Когда направление силы противоположно направлению перемещения, то сила совершает отрицательную работу, кинетическая энергия тела уменьшается.

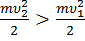
Поскольку теорема о кинетической энергии получена при помощи второго закона Ньютона, она справедлива независимо от того, какие силы действуют на тело: силы трения, силы упругости или сила тяжести (частный случай силы всемирного тяготения).

Если покоящемуся телу (υ₀ = 0) массой m необходимо сообщить скорость υ, нужно совершить определенную работу А.

Из теоремы о кинетической энергии следует:

Кинетическая энергия тела массой m, движущегося со скоростью υ, равна работе, которую должна совершить сила, действующая на покоящееся тело, чтобы сообщить ему эту скорость.

Источник

Кинетическая энергия

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

Содержание

История

Впервые понятие кинетической энергии было введено в трудах Г. Лейбница, посвященных понятию «живой силы»

Физический смысл

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим:

Если система замкнута, то есть , то , а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

— масса тела

— скорость центра масс тела

— момент инерции тела

— угловая скорость тела.

Физический смысл работы

Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:

Релятивизм

При скоростях, близких к скорости света, кинетическая энергия любого объекта равна

— масса объекта;

— скорость движения объекта в инерциальной системе отсчета;

— скорость света в вакууме ( — энергия покоя).

Данную формулу можно переписать в следующем виде:

При малых скоростях () последнее соотношение переходит в обычную формулу .

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — Постоянная Больцмана.

См. также

Полезное

Смотреть что такое «Кинетическая энергия» в других словарях:

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, энергия, которой обладает движущийся предмет. Получает ее, начав двигаться. Зависит от массы ( ) предмета и его скорости (v), согласно равенству: К. э. = 1/2mv2. При ударе преобразуется в другую форму энергии, такую как… … Научно-технический энциклопедический словарь

Кинетическая энергия — КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, механическая энергия системы, зависящая от скоростей движения составляющих ее частей. В классической механике кинетическая энергия материальной точки массы m, движущейся со скоростью v, равна 1/2 от mv2. В сумме с… … Иллюстрированный энциклопедический словарь

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — энергия механич. системы, зависящая от скоростей её точек. К. э. Т матер. точки равна: T=mv2/2, где m масса этой точки, v её скорость. К. э. механич. системы равна сумме К. э. всех её точек: T=Smkv2k/2. Выражение К. э. системы можно ещё… … Физическая энциклопедия

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — энергия механической системы, зависящая от скоростей движения составляющих ее частей. В классической механике кинетическая энергия материальной точки массы m, движущейся со скоростью v, равна 1/2mv2 … Большой Энциклопедический словарь

кинетическая энергия — ▲ энергия ↑ скорость, масса (материи) < > потенциальная энергия кинетическая энергия энергия, определяемая скоростью тела и его массой. механическая энергия. маховик … Идеографический словарь русского языка

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — (энергия движения) запас энергии движущегося тела, превращающийся в другой вид энергии при прекращении движения. Напр. К. Э. пули, попадающей в мишень, превращается в теплоту. При поступательном движении тела его К. Э. равна половине произведения … Морской словарь

кинетическая энергия — Энергия, которой обладает движущееся тело; определяется как половина произведения массы на квадрат скорости. Для жидкости обычно говорят о плотности кинетической энергии мере количества энергии движения, которой обладает единица объема жидкости.… … Справочник технического переводчика

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — (см.) механического движения тела или системы тел, зависящая от скоростей их точек. К. э. поступательно движущегося тела равна половине произведения массы тела на квадрат его скорости: К э. системы тел равна сумме К. э. всех тел системы … Большая политехническая энциклопедия

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — сила в движении, действующая сила движения; в отличие от потенциальной энергии силы в покое. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907 … Словарь иностранных слов русского языка

Источник

Формула кинетической энергии

Определение и формула кинетической энергии

Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.

Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.

Встречаются следующие обозначения кинетической энергии: E_k,W_k,T.

Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:

Кинетическая энергия материальной точки и тела

Кинетическая энергия материальной точки равна:

где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.

Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:

В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.

При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:

Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:

Единицы измерения кинетической энергии

Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:

в системе СГС –[E_k]= эрг.

При этом: 1 дж= 10 7 эрг.

Теорема Кенига

Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой, кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения системы со скоростью центра масс (v_c) и кинетической энергии (E’_k) системы при ее относительном движении к поступательному перемещению системы отсчета. При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:

Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:

Примеры решения задач

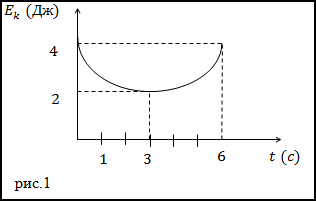
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени), при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?

Решение. По определению изменение кинетической энергии равно работе (A’), которая производится над телом при силовом взаимодействии, то есть можно записать, что:

Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:

Ответ. A’=-2 Дж.

Формула кинетической энергии не по зубам? Тебе ответит эксперт через 10 минут!

Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:

Но по условию задачи:

Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:

Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:

При этом нормальное ускорение частицы (a_n), перемещающейся по окружности найдем как:

Тангенциальную составляющую ускорения (a_т)используя определение тангенциального ускорения, определение скорости ($v=\frac$) и выражение v(s) (2.3) вычислим как:

Используем выражения: (2.5), (2.6), (2.7), окончательно получаем для модуля силы:

Источник

Кинетическая энергия
		E k = 1 / 2 м v 2 E k = E t + E r

Часть серии по
Классическая механика
F знак равно d d т ( м v ) <\ displaystyle <\ textbf > = <\ frac > (м <\ textbf >)> СОДЕРЖАНИЕ История и этимология Обзор Ньютоновская кинетическая энергия Кинетическая энергия твердых тел E k знак равно 1 2 м v 2 <\ displaystyle E _ <\ text > = <\ frac <1><2>> mv ^ <2>> Например, можно рассчитать кинетическую энергию массы 80 кг (около 180 фунтов), движущейся со скоростью 18 метров в секунду (около 40 миль в час или 65 км / ч), как Поскольку кинетическая энергия увеличивается пропорционально квадрату скорости, объект, удваивающий свою скорость, имеет в четыре раза больше кинетической энергии. Например, автомобилю, движущемуся в два раза быстрее, чем другому, требуется в четыре раза больше расстояния для остановки, при условии постоянного тормозного усилия. Как следствие этого четырехкратного увеличения, для удвоения скорости требуется в четыре раза больше работы. Кинетическая энергия объекта связана с его импульсом уравнением: E k знак равно п 2 2 м <\ displaystyle E _ <\ text > = <\ frac > <2m>>> E т знак равно 1 2 м v 2 <\ displaystyle E _ <\ text> = <\ frac <1><2>> mv ^ <2>> Вывод Применяя товарное правило, мы видим, что: Следовательно, (в предположении постоянной массы, так что dm = 0), мы имеем, Вращающиеся тела Если твердое тело Q вращается вокруг любой линии, проходящей через центр масс, то оно имеет кинетическую энергию вращения ( ), которая представляет собой просто сумму кинетических энергий его движущихся частей и, таким образом, определяется выражением: E р <\ displaystyle E _ <\ text > \,> E р знак равно ∫ Q v 2 d м 2 знак равно ∫ Q ( р ω ) 2 d м 2 знак равно ω 2 2 ∫ Q р 2 d м знак равно ω 2 2 я знак равно 1 2 я ω 2 <\ displaystyle E _ <\ text > = \ int _ <\ frac dm> <2>> = \ int _ <\ frac <(r \ omega) ^ <2>dm> <2>> = <\ frac <\ omega ^ <2>> <2>> \ int _ > dm = <\ frac <\ omega ^ <2>> <2>> I = <\ frac <1><2>> I \ omega ^ <2>> Кинетическая энергия систем Динамика жидкостей В гидродинамике кинетическая энергия на единицу объема в каждой точке поля потока несжимаемой жидкости называется динамическим давлением в этой точке. E k знак равно 1 2 м v 2 <\ displaystyle E _ <\ text > = <\ frac <1><2>> mv ^ <2>> Разделив на V, единица объема: Точка зрения Таким образом, кинетическая энергия системы является наименьшей по отношению к системе отсчета центра импульса, т. Е. Системе отсчета, в которой центр масс неподвижен (либо система отсчета центра масс, либо любая другая система отсчета центра импульса ). В любой другой системе отсчета существует дополнительная кинетическая энергия, соответствующая общей массе, движущейся со скоростью центра масс. Кинетическая энергия системы в центре системы отсчета импульса является величиной, которая инвариантна (все наблюдатели видят ее одинаковую). Вращение в системах Иногда бывает удобно разделить полную кинетическую энергию тела на сумму поступательной кинетической энергии центра масс тела и энергии вращения вокруг центра масс ( энергия вращения ): E k знак равно E т + E р <\ displaystyle E _ <\ text > = E _ <\ text> + E _ <\ text >> Релятивистская кинетическая энергия твердых тел. Упрощая выражение, получаем что приводит к формуле Эта формула показывает, что работа, затрачиваемая на ускорение объекта из состояния покоя, приближается к бесконечности, когда скорость приближается к скорости света. Таким образом, невозможно ускорить объект через эту границу. E отдыхать знак равно E 0 знак равно м c 2 <\ displaystyle E _ <\ text > = E_ <0>= mc ^ <2>> На небольшой скорости ( v ≪ c ) релятивистская кинетическая энергия хорошо аппроксимируется классической кинетической энергией. Это делается с помощью биномиального приближения или путем принятия первых двух членов разложения Тейлора за обратный квадратный корень: Таким образом, полную энергию можно разделить на энергию массы покоя плюс ньютоновскую кинетическую энергию на малых скоростях. E k <\ displaystyle E_ > Когда объекты движутся со скоростью, намного меньшей, чем скорость света (например, в повседневных явлениях на Земле), первые два члена ряда преобладают. Следующий член в приближении ряда Тейлора мала для низких скоростей. Например, для скорости 10 км / с (22000 миль / ч) поправка к ньютоновской кинетической энергии составляет 0,0417 Дж / кг (при ньютоновской кинетической энергии 50 МДж / кг), а для скорости 100 км / с это 417 Дж / кг (при ньютоновской кинетической энергии 5 ГДж / кг). Релятивистская связь между кинетической энергией и импульсом дается выражением Это говорит о том, что формулы для энергии и импульса не являются специальными и аксиоматическими, а являются концепциями, вытекающими из эквивалентности массы и энергии и принципов относительности. Общая теория относительности Используя соглашение, что Если частица имеет импульс а кинетическая энергия может быть выражена как полная энергия за вычетом энергии покоя: Решение для u t дает Таким образом, для неподвижного наблюдателя ( v = 0) и, таким образом, кинетическая энергия принимает вид Выделение остаточной энергии дает: Это выражение сводится к частному релятивистскому случаю для метрики плоского пространства, где В ньютоновском приближении ОТО Кинетическая энергия в квантовой механике Источник ← видуар медицинский что это такое выдвижная морозильная камера в холодильнике что это → Вам также понравится что нужно сделать чтоб квас был резким 05.01.202420.04.2022 admin 0 к чему снится терять волосы на голове 03.01.202406.04.2022 admin 0 водитель маршрутного такси сказал вновь вошедшим пассажирам что оплатите проезд 04.01.202411.04.2022 admin 0 Добавить комментарий Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.