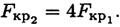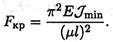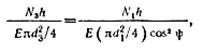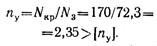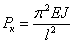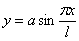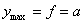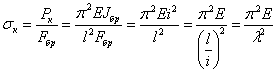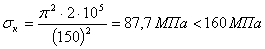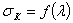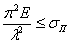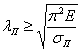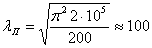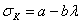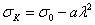в чем измеряется гибкость стержня

Что такое жесткость и гибкость элементов

Разницу в работе гибких и жестких стержней под воздействием нагрузки люди заметили достаточно давно. Так один из мастеров восточных единоборств, гуляя по зимнему саду, сделал примерно следующий вывод: жесткая сухая ветка под тяжестью налипшего снега ломается, а гибкая ветка прогибается и, сбросив налипший снег, возвращается в прежнее положение с минимумом повреждений.

Если перевести это гибкую поэтическую аллегорию, помогавшую мастеру восточных единоборств привлекать новых учеников, на современный жесткий язык теории сопротивления материалов, то звучать это будет примерно так: если напряжения в рассматриваемом поперечном сечении жесткого элемента конструкции превышают значение нормативного сопротивления, то это приведет сначала к значительным пластическим деформациям, а затем, при увеличении напряжений, и к разрушению жесткого элемента (будет это разрушение хрупким или вязким, принципиального значения не имеет). В то же время гибкий элемент конструкции под действием такой же нагрузки, не разрушится, но потеряет устойчивость.

Конечно же мне, как и любому другому обычному человеку, гораздо ближе и понятнее определение жесткости и гибкости, данное средневековым мастером восточных единоборств. Но справедливости ради следует отметить, что этот мастер сильно перегнул палку (точнее ветку или, выражаясь языком строительной механики, стержень). Дело в том, что гибкий стержень потеряет устойчивость задолго до того, как значение нагрузки в переводе на напряжения в рассматриваемом сечении достигнет уровня нормативного сопротивления.

Чтобы было более понятно, о чем идет речь, приведу еще один пример.

Если взять достаточно ровный человеческий волос со среднестатистического человека длиной 10 см и попробовать его разорвать руками, то это будет не так уж и просто, для этого следует приложить достаточно большую физическую силу, или выражаясь по-научному, создать достаточно большие растягивающие напряжения в волосе или растягивающую силу около 5 кг (может больше, может меньше, не в этом суть).

А вот если мы попробуем поставить этот волос в вертикальное положение, например, на стол, то волос стоять не будет, а будет сгибаться под действием своего собственного веса, вряд ли превышающего несколько миллиграмм, даже если мы обеспечим ему такое закрепление на верхней опоре, при котором верх волоса не сможет смещаться в горизонтальном направлении, но сможет смещаться в вертикальном направлении.

Вот такое, условно говоря, сгибание и означает потерю устойчивости. Таким образом использовать очень гибкие стержни в качестве сжатых элементов строительных конструкций не имеет никакого смысла.

Между тем, если мы отрежем от этого же волоса кусок длиной 1 см, то этот кусок уже будет сгибаться не так сильно под действием собственного веса и будет обладать некоторой устойчивостью, а если это будет волос длиной 2-5 мм, то об него уже можно сильно уколоться, а волос при этом даже и не согнется.

Как, надеюсь, понятно из вышеприведенного примера, даже для стержня с постоянными геометрическими характеристиками поперечного сечения (радиусом инерции и моментом инерции) его устойчивость зависит от расчетной длины стержня. Другими словами один и тот же стержень может быть и гибким и жестким в зависимости от его расчетной длины.

Для того, чтобы определить гибкость элемента, достаточно расчетную длину элемента l_o разделить на радиус инерции i поперечного сечения (при условии, что параметры поперечных сечений постоянны по всей длине элемента):

Примечание: в различных нормативных документах указанные характеристики могут иметь и другие обозначения, но принципиального значения это не имеет.

Таким образом чем меньше гибкость элемента, тем он более жесткий, соответственно чем больше гибкость элемента, тем более он гибкий. А чтобы определить, не является ли такая гибкость чрезмерной для рассматриваемого элемента конструкции, используются таблицы из соответствующих нормативных документов.

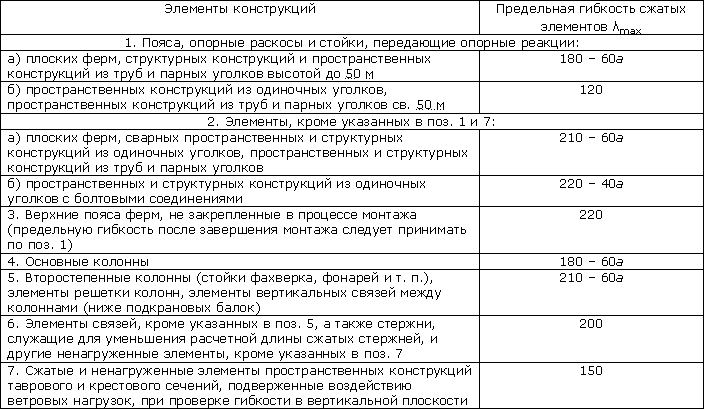
Например, при расчете сжатых элементов стальных конструкций используется такая таблица:

Таблица 19* (согласно СНиП II-23-81 (1990))

А при расчете деревянных конструкций, такая:

Таблица 251.1. Предельные значения гибкости (согласно СНиП II-25-80 (1988))

На значение гибкости влияет и модуль упругости материала. Чем меньше значение модуля упругости, тем больше может быть гибкость. В связи с этим предельно допустимые значения гибкости могут быть разные для элементов из различных материалов, что и отражено в указанных таблицах.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

Примеры решения задач. Пример 1. Рассчитать гибкость стержня

Пример 1. Рассчитать гибкость стержня. Круглый стержень диаметром 20 мм закреплен так, как показано на рис. 37.1.

Решение

1. Гибкость стержня определяется по формуле

2. Определяем минимальный радиус инерции для круга.

Подставив выражения для J_min и А (сечение круг)

Пример 2. Как изменится критическая сила для стержня, ес­ли изменить способ закрепления концов? Сравнить представленные схемы (рис. 37.2)

Решение

Критическая сила увеличится в 4 раза.

Пример 3. Как изменится критическая сила при расчете на устойчивость, если стержень двутаврового сечения (рис. 37.3а, дву­тавр № 12) заменить стержнем прямоугольного сечения той же пло­щади (рис. 37.3б)? Остальные параметры конструкции не меняются. Расчет выполнить по формуле Эйлера.

Решение

1. Определим ширину сечения прямоугольника, высота сечения равна высоте сечения двутавра. Геометрические параметры двутавра № 12 по ГОСТ 8239-89 следующие:

площадь сечения А₁ = 14,7см 2 ;

По условию площадь прямоугольного сечения равна площади сечения двутавра. Определяем ширину полосы при высоте 12 см.

2. Определим минимальный из осевых моментов инерции.

3. Критическая сила определяется по формуле Эйлера:

4. При прочих равных условиях отношение критических сил рав­но отношению минимальных моментов инерции:

5. Таким образом, устойчивость стержня с сечением двутавр № 12 в 15 раз выше, чем устойчивость стержня выбранного пря­моугольного сечения.

Пример 4. Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение — швеллер № 16, материал — СтЗ, запас устойчивости трехкратный. Стержень нагружен сжима­ющей силой 82 кН (рис. 37.4).

Решение

1. Определяем основные геометрические пара­метры сечения стержня по ГОСТ 8240-89. Швеллер № 16: площадь сечения 18,1см 2 ; минимальный осевой момент сечения 63,3 см 4 ; мини­мальный радиус инерции сечения г_т;_п = 1,87см.

2. Определяем категорию стержня в зависимости от гибкости.

Предельная гибкость для материала СтЗ λ_пред = 100.

Расчетная гибкость стержня при длине l = 1м = 1000мм

Рассчитываемый стержень — стержень большой гибкости, рас­чет ведем по формуле Эйлера.

3. Допускаемая нагрузка на стержень

4. Условие устойчивости

Решение

Для расчёта на устойчивость должна быть известна критическая сила для заданной стойки. Необходимо установить, по какой формуле следует вычислять критическую силу, т. е. надо сопоставить гибкость стойки с предельной гибкостью для её материала.

Вычисляем величину предельной гибкости, так как табличных данных о λ,_пред для материала стойки не имеется:

Для определения гибкости рассчитываемой стойки вычисляем геометрические характеристики ее поперечного сечения:

Определяем гибкость стойки:

и убеждаемся, что λ [n_у] на 5,2%.

Пример 2.87. Проверить на прочность и устойчи­вость заданную стержневую систему (рис. 2.86), Материал стержней — сталь Ст5 (σ_т = 280 Н/мм 2 ). Требуемые коэффи­циенты запаса: прочности [n] = 1,8; устойчивости [n_у] = 2,2. Стержни имеют круглое поперечное сечение d₁ = d₂ = 20 мм, d₃ = 28 мм.

Решение

Вырезая узел, в котором сходятся стержни, и составляя уравнения равновесия для действующих на него сил (рис. 2.86)

устанавливаем, что заданная система статически неопре­делима (три неизвестных усилия и два уравнения ста­тики). Ясно, что для расчета стержней на прочность и устойчивость необходимо знать величины продольных сил, возникающих в их поперечных сечениях, т. е. нужно раскрыть статическую неопределимость.

Составляем уравнение перемещений на основе диа­граммы перемещений (рис. 2.87):

или, подставляя значения изменений длин стержней, по­лучаем

Решив это уравнение совместно с уравнениями ста­тики, найдем:

Напряжения в поперечных сечениях стержней 1 и 2 (см. рис. 2.86):

Их коэффициент запаса прочности

Для определения коэффициента запаса устойчивости стержня 3 надо вычислить критическую силу, а это тре­бует определения гибкости стержня, чтобы решить, какой формулой для нахождения N_Kp следует воспользоваться.

Коэффициент запаса устой­чивости

Таким образом, расчет пока­зывает, что коэффициент запаса устойчивости близок к требуемо­му, а коэффициент запаса проч­ности значительно выше требуемого, т. е. при увеличении нагрузки системы потеря устойчивости стержнем 3 вероят­нее, чем возникновение текучести в стержнях 1 и 2.

Источник

Понятие о гибкости стержня

Глава 13. Анализ формулы Эйлера

Значениям критической силы высших порядков соответствуют искривления по синусоидам с двумя, тремя и т. д. полуволнами (Рис.13.1):

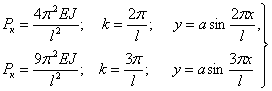(13.1)

Таким образом, чем больше точек перегиба будет иметь синусоидально-искривленная ось стержня, тем большей должна быть критическая сила. Более полные исследования показывают, что формы равновесия, определяемые формулами (13.1), неустойчивы; они переходят в устойчивые формы лишь при наличии промежуточных опор в точках В и С (рис.13.1).

Рис. 13.1

Наименьшая критическая сила определяется формулой

а изогнутая ось представляет синусоиду

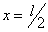
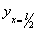
Величина постоянной интегрирования а осталась неопределенной; физическое значение ее выяснится, если в уравнении синусоиды положить ; тогда (т. е. посредине длины стержня) получит значение:

Значит, а — это прогиб стержня в сечении посредине его длины. Так как при критическом значении силы Р равновесие изогнутого стержня возможно при различных отклонениях его от прямолинейной формы, лишь бы эти отклонения были малыми, то естественно, что прогиб f остался неопределенным.

Он должен быть при этом настолько малым, чтобы мы имели право применять приближенное дифференциальное уравнение изогнутой оси, т. е. чтобы 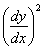было по прежнему мало по сравнению с единицей.

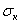
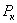
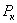
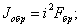
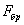
Получив значение критической силы, мы можем сейчас же найти и величину критического напряжения , разделив силу на площадь сечения стержня F; так как величина критической силы определялась из рассмотрения деформаций стержня, на которых местные ослабления площади сечения сказываются крайне слабо, то в формулу для входит момент инерции поэтому принято при вычислении критических напряжений, а также при составлении условия устойчивости вводить в расчет полную, а не ослабленную, площадь поперечного сечения стержня . Тогда

Таким образом, критическое напряжение для стержней данного материала обратно пропорционально квадрату отношения длины стержня к наименьшему радиусу инерции его поперечного сечения. Это отношение называется гибкостью стержня и играет весьма важную роль во всех проверках сжатых стержней на устойчивость.

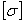
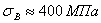
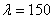
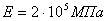
Из последнего выражения видно, что критическое напряжение при тонких и длинных стержнях может быть весьма малым, ниже основного допускаемого напряжения на прочность . Так, для стали 3 с пределом прочности допускаемое напряжение может быть принято ; критическое же напряжение для стержня с гибкостью при модуле упругости материала будет равно

Таким образом, если бы площадь сжатого стержня с такой гибкостью была подобрана лишь по условию прочности, то стержень разрушился бы от потери устойчивости прямолинейной формы.

Глава 14. Пределы применимости формулы Эйлера. Формула Ф. Ясинского.

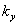
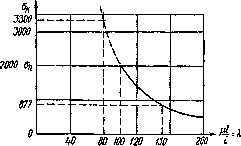
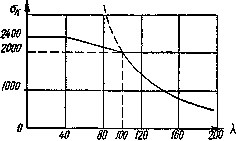
Казалось бы, что полученные в предыдущих параграфах результаты решают задачу проверки сжатого стержня на устойчивость; остается выбрать лишь коэффициент запаса . Однако это далеко не так. Ближайшее же изучение числовых величин, получаемых по формуле Эйлера, показывает, что она дает правильные результаты лишь в известных пределах.

На рис.14.1 приведена зависимость величины критических напряжений, вычисленных при различных значениях гибкости для стали 3, обычно применяемой в металлических конструкциях. Эта зависимость представляется гиперболической кривой, так называемой «гиперболой Эйлеpa»:

При пользовании этой кривой надо вспомнить, что представляемая ею формула 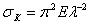получена при помощи интегрирования дифференциального уравнения изогнутой оси, т. е. в предположении, что напряжения в стержне в момент потери устойчивости не превосходят предела пропорциональности.

Рис. 14.1. Гиперболическая зависимость критического напряжения от гибкости стержня

Следовательно, мы не имеем права пользоваться величинами критических напряжений, вычисленных по формуле Эйлера, если они получаются выше этого предела для данного материала. Иначе говоря, формула Эйлера применима лишь при соблюдении условия:

или

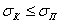
Если из этого неравенства выразить гибкость 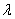, то условие применимости формул Эйлера получит иной вид:

Подставляя соответствующие значения модуля упругости и предела пропорциональности для данного материала, находим наименьшее значение гибкости, при которой еще можно пользоваться формулой Эйлера. Для стали 3 предел пропорциональности может быть принят равным 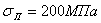, поэтому, для стержней из этого материала можно пользоваться формулой Эйлера лишь при гибкости

т. е. большей, чем 100 %

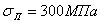
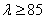
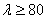
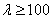
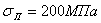
Для стали 5 при формула Эйлера применима при гибкости ; для чугуна — при , для сосны — при и т. д. Если мы на Рис.14.1 проведем горизонтальную линию с ординатой, равной , то она рассечет гиперболу Эйлера на две части; пользоваться можно лишь нижней частью графика, относящейся к сравнительно тонким и длинным стержням, потеря устойчивости которых происходит при напряжениях, лежащих не выше предела пропорциональности.

Теоретическое решение, полученное Эйлером, оказалось применимым на практике лишь для очень ограниченной категории стержней, а именно, тонких и длинных, с большой гибкостью. Между тем, в конструкциях очень часто встречаются стержни с малой гибкостью. Попытки использовать формулу Эйлера для вычисления критических напряжений и проверки устойчивости при малых гибкостях вели иногда к весьма серьезным катастрофам, да и опыты над сжатием стержней показывают, что при критических напряжениях, больших предела пропорциональности, действительные критические силы значительно ниже определенных по формуле Эйлера.

Таким образом, надо найти способ вычисления критических напряжений и для тех случаев, когда они превышают предел пропорциональности материалов, например, для стержней из мягкой стали при гибкостях от 0 до 100.

Необходимо сразу же отметить, что в настоящее время важнейшим источником для установления критических напряжений за пределом пропорциональности, т. е. при малых и средних гибкостях, являются результаты экспериментов. Имеются попытки и теоретического решения этой задачи, но они скорее указывают путь к дальнейшим исследованиям, чем дают основания для практических расчетов.

Прежде всего надо выделить стержни с малой гибкостью, от 0 примерно до 30—40; у них длина сравнительно невелика по отношению к размерам поперечного сечения. Например, для стержня круглого сечения гибкости 20 соответствует отношение длины к диаметру, равное 5. Для таких стержней трудно говорить о явлении потери устойчивости прямолинейной формы всего стержня в целом в том смысле, как это имеет место для тонких и длинных стержней.

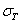
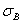
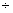
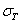
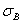
Эти короткие стержни будут выходить из строя главным образом за счет того, что напряжения сжатия в них будут достигать предела текучести (при пластичном материале) или предела прочности (при хрупких материалах). Поэтому для коротких стержней, до гибкости примерно 30 40, критические напряжения «будут равны, или немного ниже (за счет наблюдающегося все же некоторого искривления оси стержня), соответственно или (сталь), или (чугун, дерево).

Таким образом, мы имеем два предельных случая работы сжатых стержней: короткие стержни, которые теряют грузоподъемность в основном за счет разрушения материала от сжатия, и длинные, для которых потеря грузоподъемности вызывается нарушением устойчивости прямолинейной формы стержня. Количественное изменение соотношения длины и поперечных размеров стержня меняет и весь характер явления разрушения. Общим остается лишь внезапность наступления критического состояния в смысле внезапного резкого возрастания деформаций.

В сжатых стержнях большой гибкости, для которых применима формула Эйлера, после достижения силой Р критического значения обычно наблюдается резкий рост деформаций. До этого момента прогибы, как правило, растут с ростом нагрузки, но остаются незначительными. Теоретически можно было бы ожидать, что до критической силы стержень будет оставаться прямым; однако ряд неизбежных на практике обстоятельств — начальная кривизна стержня, некоторый эксцентриситет приложения нагрузки, местные перенапряжения, неоднородность материала — вызывают небольшие прогибы и при сжимающих силах, меньших критических.

Подобный же характер имеет и зависимость укорочений от напряжения при сжатии коротких стержней; мы имеет ту же внезапность роста деформаций при определенной величине напряжений (когда ).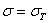

Нам остается теперь рассмотреть поведение сжатых стержней при средних величинах гибкости, например для стальных стержней при гибкостях от 40 до 100; с подобными значениями гибкостей инженер чаще всего встречается на практике.

По характеру разрушения эти стержни приближаются к категории ^ тонких и длинных стержней; они теряют свою прямолинейную форму и разрушаются при явлениях значительного бокового выпучивания. При опытах для них можно отметить наличие ясно выраженной критической силы в «эйлеровом» смысле; критические напряжения получаются выше предела пропорциональности и ниже предела текучести для пластичных и предела прочности для хрупких материалов.

Однако потеря прямолинейной формы и понижение критических напряжений по сравнению с короткими стержнями для этих стержней «средней» гибкости связаны с такими же явлениями нарушения прочности материала, какие вызывают потерю грузоподъемности в коротких стержнях. Здесь комбинируются и влияние длины, понижающее величину критических напряжений, и влияние значительного роста деформаций материала при напряжениях за пределом пропорциональности.

Экспериментальное определение критических сил для сжатых стержней производилось неоднократно как у нас, так и заграницей. Особенно обширный опытный материал собрал проф. Ф. Ясинский, составивший таблицу критических («ломающих») напряжений в. зависимости от гибкости для целого ряда материалов и положивший начало современным методам расчета сжатых стержней на устойчивость.

На основании полученного опытного материала можно считать, что при критических напряжениях, меньших предела пропорциональности, все эксперименты подтверждают формулу Эйлера для любого материала.

Для стержней средней и малой гибкости были предложены различные эмпирические формулы, показывающие, что критические напряжения при таких гибкостях меняются по закону, близкому к линейному:

где а и b — коэффициенты, зависящие от материала, a — гибкость стержня. Для литого железа Ясинский получил: а = 338,7МПа, b = 1,483 МПа. Для стали 3 при гибкостях от = 40 до = 100 коэффициенты а и b могут быть приняты: а = 336 МПа; b = 1,47МПа. Для дерева (сосна): а = 29,3 МПа; b = 0,194 МПа.

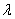
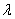
Иногда удобны эмпирические формулы, дающие для неупругой области изменение критических напряжений по закону квадратной параболы; к ним относится формула

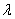
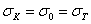
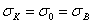
Здесь при = 0 считают для пластичного и для хрупкого материала; коэффициент а, подобранный из условия плавного сопряжения с гиперболой Эйлера, имеет значение:

Для стали с пределом текучести 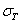= 280 МПа а = 0,009 МПа

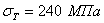
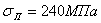
При наличии приведенных здесь данных может быть построен полный график критических напряжений (в зависимости от гибкости) для любого материала. На Рис.2 приведен такой график для строительной стали с пределом текучести и пределом пропорциональности .

Рис. 14.2. Полный график критических напряжений для строительной стали.

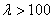
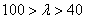
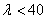
График состоит из трех частей: гиперболы Эйлера при , наклонной прямой при и горизонтальной, или слабо наклонной, прямой при . Подобные же графики можно построить, комбинируя формулу Эйлера с результатами экспериментов, и для других материалов.

Таким образом, можно считать, что задача определения критических напряжений для стержней любой гибкости решена с достаточной для практических целей точностью.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник