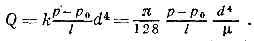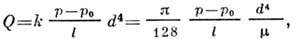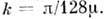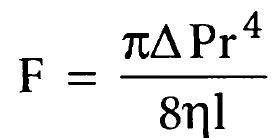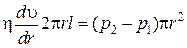в чем измеряется формула пуазейля

Вязкое движение жидкости. Формула Пуазейля. Число Рейнольдса, его физический смысл.

Если вертикальный цилиндрический сосуд наполненный жидкостью равномерно вращать вокруг своей оси, то жидкость также приходит во вращение. Сначала начинают двигаться слои, находящиеся ближе к вертикальной поверхности сосуда. Затем вращение передается внутренним слоям. Вскоре жидкость начнет вращаться равномерно, как твердое тело. Это говорит о том, что существуют некие касательные силы между сосудом и жидкостью, а так же между слоями жидкости. Эти касательные силы называются силами трения – внутренними (между слоями жидкости) и внешними (между жидкостью и стенкой сосуда). Силы внутреннего трения – силы вязкости.

где – расстояние между пластинками; – постоянная, называемая вязкостью жидкости. зависит от материала пластинок и имеет различные значения для различных жидкостей. Для конкретной жидкости зависит от различных параметров, характеризующих ее внутреннее состояние (в первую очередь от температуры).

Закон подобия течений ­– если для двух течений пять из шести безразмерных комбинаций совпадают, то будут совпадать и шестые. Такие течения называются механически или гидродинамически подобными.

Число Рейнольдса – отношение кинетической энергии жидкости к потере ее, обусловленной работой сил вязкости на характерной длине.

Таким образом, оно определяет относительную роль инерции и вязкости жидкости при течении. При больших числах Рейнольдса основную роль играет инерция при малых – вязкость.

Аналогичный смысл имеет число Фруда F. Оно по порядку величины определяет отношение кинетической энергии жидкости к приращению ее, обусловленному работой силы тяжести на пути, равному характерной длине. Чем больше число Фруда, тем больше роль инерции по сравнению с тяжестью, и наоборот.

Источник

ПУАЗЁЙЛЯ ЗАКОН

П. з. применим только при ламинарном течении жидкости и при условии, что длина трубки превышает т. н. длину нач. участка, необходимую для развития ламинарного течения в трубке. Течение, подчиняющееся П. з., паз. течением Пуазёйля; оно характеризуется параболич. распределением скорости по радиусу трубки д : 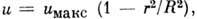где и— скорость на расстоя-

Полезное

Смотреть что такое «ПУАЗЁЙЛЯ ЗАКОН» в других словарях:

ПУАЗЁЙЛЯ ЗАКОН — [по имени франц. учёного Ж. Л. Пуазёйля (J. L. Poiseuille; 1799 1869)] закон ламинарного течения вязкой жидкости в тонкой цилиндрич. трубке. Согласно П. з., объёмный расход жидкости сквозь поперечное сечение трубки О = ПИ*Дельта р*r4/8 nl, где r… … Большой энциклопедический политехнический словарь

Пуазёйля закон — закон истечения жидкости через тонкую цлиндрическую трубку: объем Q жидкости, протекшей за секунду через поперечное сечение трубки, прямо пропорционально разности давлений ρ и ρ0 у входа в трубку и на выходе из нее и четвертой степени… … Большая советская энциклопедия

Закон Пуазёйля — (иногда закон Хагена Пуазёйля) это физический закон так называемого течения Пуазёйля, то есть установившегося течения вязкой несжимаемой жидкости в тонкой цилиндрической трубке. Закон установлен эмпирически в 1839 году Г. Хагеном, а в … Википедия

Течение Пуазёйля — Параболическое распределение скорости при течении Пуазейля. Пропеллеры показывают, что у этого течения ненулевая завихрённость. Течение Пуазёйля ламинарное течение жидкости через каналы в виде прямого кругового цилиндра или слоя между… … Википедия

Формула Пуазёйля — аналитическое выражение закона Пуазёйля (Хагена Пуазёйля): При установившемся ламинарном движении вязкой несжимаемой жидкости сквозь цилиндрическую трубу круглого сечения секундный объёмный расход прямо пропорционален перепаду давления на единицу … Википедия

Пуазёйль Жан Луи Мари — Пуазёйль, Пуазёй (Poiseuille) Жан Луи Мари (22.4.1799, Париж, 26.12.1869, там же), французский врач и физик, член Французской медицинской академии (с 1842). П. принадлежат работы по вопросам кровообращения и дыхания. Впервые применил (1828)… … Большая советская энциклопедия

Пуазёйль — Пуазёй (Poiseuille) Жан Луи Мари (22.4.1799, Париж, 26.12.1869, там же), французский врач и физик, член Французской медицинской академии (с 1842). П. принадлежат работы по вопросам кровообращения и дыхания. Впервые применил (1828) ртутный … Большая советская энциклопедия

Пуазёйль — Пуазёйль, Жан Луи Мари Жан Луи Мари Пуазёйль фр. Jean Louis Marie Poiseuille Дата рождения … Википедия

Пуазёйль Жан Луи Мари — Пуазёй (Poiseuille) (1799 1869), французский врач и физик. Труды по физиологии дыхания, динамике кровообращения. Первым применил (1828) ртутный манометр для измерения кровяного давления животных. Экспериментально установил закономерности… … Энциклопедический словарь

Источник

В чем измеряется формула пуазейля

Причину такого значительного возрастания объемного кровотока при увеличении диаметра сосуда можно объяснить с помощью схемы, представленной на рисунке. На схеме показано поперечное сечение крупного и мелкого кровеносных сосудов. Концентрические слои внутри сосудов указывают на то, что скорость движения каждого слоя отличается от скорости соседних слоев, т.к. происходит ламинарное течение крови (см. ранее в статьях на сайте). Дело в том, что слой крови, прилежащий к стенке сосуда, едва движется благодаря взаимодействию крови и эндотелия сосудистой стенки. Следующий слой крови скользит относительно пристеночного слоя и поэтому движется быстрее. Третий, четвертый, пятый и шестой слои также текут с нарастающей скоростью. Таким образом, пристеночный слой крови движется чрезвычайно медленно, в то время как по продольной оси сосуда кровь движется с наибольшей скоростью.

А. Влияние диаметра сосуда на объемный кровоток.
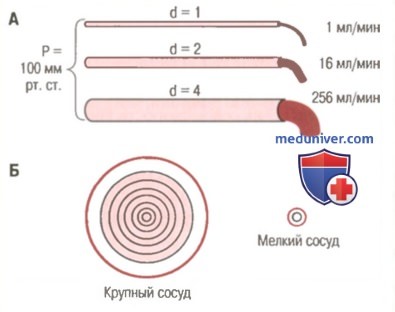
Б. Концентрические слои крови, текущие вдоль сосуда с разной скоростью; поток тем быстрее, чем дальше от стенки сосуда

В мелких сосудах практически вся кровь оказывается вблизи сосудистой стенки, поэтому быстротекущего центрального потока крови просто не существует. Сложив скорости всех концентрических слоев текущей крови, умноженные на площади поперечного сечения каждого слоя, можно вывести формулу, известную как закон Пуазейля:

где F — скорость кровотока, ΔР — разница давления на концах сосуда, r — радиус сосуда, 1 — длина сосуда и n — вязкость крови.

Обратите внимание, что в этом уравнении скорость кровотока прямо пропорциональна четвертой степени радиуса сосуда. Это еще раз показывает, что среди всех факторов, определяющих скорость кровотока, диаметр кровеносного сосуда, равный двум радиусам, имеет первостепенное значение.

Влияние диаметра артериол на их сопротивление (закон четвертой степени). В большом круге кровообращения почти 2/3 общего периферического сопротивления приходится на мелкие артериолы. Внутренний диаметр артериол имеет величину от 4 до 25 мкм. Однако мощная мышечная стенка артериол позволяет существенно менять внутренний диаметр, часто более чем в 4 раза. Исходя из закона четвертой степени, который определяет зависимость объемного кровотока от диаметра сосудов, четырехкратное увеличение диаметра приводит к возрастанию объемного кровотока, по меньшей мере, в 256 раз. Таким образом, незначительные изменения диаметра артериол в ответ на нервные сигналы или действие местных гуморальных факторов может привести или к почти полному прекращению кровотока в тканях, или — в других экстремальных ситуациях — резко увеличить кровоток. И действительно, в отдельных сосудистых областях регистрируется увеличение местного кровотока в 100 раз при переходе артериол из состояния максимального сужения к состоянию их максимального расширения.

Сопротивление сосудов, соединенных между собой последовательно и параллельно. Кровь, которая поступает в большой круг кровообращения из сердца, движется из области с высоким давлением (аорта) в область с низким давлением крови (полые вены). Кровь течет через обширную сосудистую сеть, в которой многочисленные сосуды соединены между собой последовательно и параллельно. Артерии, артериолы, капилляры, венулы и вены в целом являются системой последовательно соединенных сосудов. Общее сопротивление такой системы представляет собой сумму сопротивлений каждого отдельного сосуда:
R_общее = R1+R2+R3+R4.

Сосудистое сопротивление при последовательном (А) и параллельном (Б) соединении сосудов

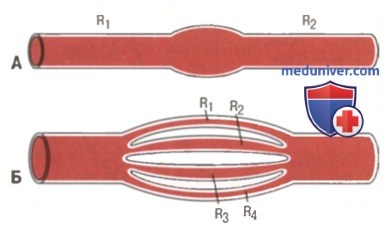
Следовательно, общее периферическое сопротивление равно сумме сопротивлений артерий, артериол, капилляров, венул и вен. На примере, приведенном на рисунке, общее сосудистое сопротивление равно сумме сопротивлений R1 и R2.

Благодаря разветвлению сосудов формируются параллельные сосудистые сети, снабжающие кровью многочисленные органы и ткани организма. Формирование параллельных сосудистых сетей позволяет каждому органу и даже участку органа в большой степени регулировать собственный местный кровоток независимо от других органов и тканей.

Для параллельно соединенных сосудов общее сопротивление рассчитывается следующим образом:
1/R_общее = 1/R₁ + 1/R₂ + 1/R₃ + 1/R₄.

Очевидно, что при одном и том же градиенте давления гораздо больший объем крови будет протекать через систему параллельных сосудов, чем через любой отдельно взятый сосуд. Таким образом, общее сопротивление системы параллельных сосудов оказывается гораздо меньше, чем сопротивление любого отдельного сосуда. Кровоток через каждый из параллельных сосудов на рисунке зависит от градиента давления и сопротивления данного сосуда, а не сопротивления всей системы. Однако увеличение сопротивления одного из сосудов параллельной системы приведет к увеличению сопротивления всей системы.

Кажется парадоксальным, что дополнительное увеличение количества сосудов в параллельной системе приводит к уменьшению общего сосудистого сопротивления. Дело в том, что множество параллельных сосудов облегчает протекание крови через сосудистую сеть, т.к. каждый параллельный сосуд обеспечивает дополнительный путь кровотоку, увеличивая так называемую проводимость системы для крови.

Итак, общая проводимость системы параллельных сосудов (Собщая) представляет собой сумму проводимостей каждого отдельного сосуда: Собщее = С1+С2+С3+С4.

Например, сосуды головного мозга, почек, мышц, желудочно-кишечного тракта, кожи, сердца представляют собой отдельные, параллельно соединенные системы, каждая из которых вносит свой вклад в общую проводимость большого круга кровообращения. Объемный кровоток каждого органа является частью общего кровотока (сердечного выброса) и зависит от сопротивления кровотоку (или проводимости) органа так же, как и от градиента давления. Следовательно, ампутация конечности или хирургическое удаление почки приводит к удалению одной из параллельных сосудистых систем большого круга кровообращения и уменьшает общую сосудистую проводимость и объемный кровоток (т.е. сердечный выброс), в то время как общее периферическое сопротивление увеличивается.

Редактор: Искандер Милевски. Дата обновления публикации: 18.3.2021

— Вернуться в оглавление раздела «Физиология человека.»

Источник

Формула Пуазейля

Течение вязких жидкостей и газов в трубах.

При течении реальных жидкостей слои в этих жидкостях движутся с различными скоростями. Вблизи стенки канала (трубы), в котором течет жидкость, скорость течения намного меньше, чем вдали от нее. Из слоя газа с большой скоростью движения переносится импульс (ко­личество движения) к слою, движущемуся с меньшей скоростью. За счет передачи импульса от одного слоя к другому поперек движения скорость движения слоев уменьшается.

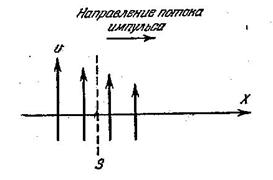
Рассмотрим течение жидкости вблизи плоской поверхности (рис.6.3). В направлении, перпендикулярном оси X, скорость движения во всех точках одинакова. Это значит, что скорость υявляется функцией только х. Как показывает опыт, импульс P, переносимый в единицу времени через единицу площади сечения, перпендику­лярного оси X, определяется уравнением

, (6.10)

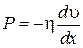
Вязкость проявляется в том, что любой слой газа или жидкости, движущийся относительно соседнего, испытывает действие некоторой силы. Эта сила и представляет собой силу трения между слоями газа.Уравнение (6.10) следует поэтому записать в виде

, (6.11)

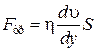
Коэффициент динамической вязкости h согласно (6.11) численно равен силе трения между слоями площадью 1 м 2 при величине гра­диента скорости (в направлении, перпендикулярном к слоям), равном единице (1 м/сек на 1 м длины). Размерность h в СИ [h]= Па · с (паскаль-секунда).

В случае стационарного ламинарного течения жидкости по трубке небольшого радиуса R объем жидкости, протекший за секунду через сечение трубки прямо пропорционален разности давлений p₁ и p₂ у входа в трубку и на выходе из нее, четвертой степени радиуса R трубки и обратно пропорционален длине l трубки и коэффициенту вязкости h

, (6.12)

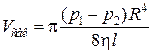
где V_сек – секундный расход жидкости. Соотношение (6.12) представляет собой формулу Пуазейля. Формула Пуазейля используется для определения коэффициента динамической вязкости сред η путем измерения объема V вытекающей жидкости за некоторое время t при заданном перепаде давлений. Этот метод называется вискозиметрическим.

Пример 6.2. Вывод формулы Пуазейля с помощью закона Ньютона для вязкого трения

Сила F_тр, действует вдоль поверхности выделенного цилиндра с площадью S = 2plr и согласно закону Ньютона (6.11) равна

. (6.13)

.

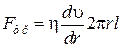
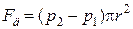
Так как F_тр,по модулю равна силе F_д, то приравнивая два последних выражения, получим

Разделяя переменные и интегрируя это уравнение, получим распределение скорости течения в радиальном направлении:

.

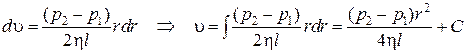
Постоянную С определим из условия равенства нулю скорости на стенке трубы:

.

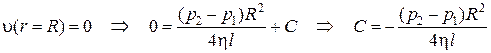
С учетом последнего равенства:

. (6.14)

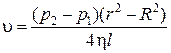
Объем жидкости dV, протекший за секунду через кольцевое сечение шириной dr (рис. 5-4), с учетом (6.14) равен:

.

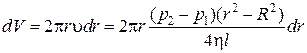
Интегрирование последнего соотношения в пределах от 0 до R приводит к формуле (6.12).

Источник

ФОРМУЛА ПУАЗЕЙЛЯ

Рассмотрим ламинарное течение вязкой жидкости по трубе радиусом R. Очевидно, что слои жидкости в трубе, будут представлять собой цилиндры, расположенные коаксиально по отношению к геометрической оси трубы. Скорости разных слоев жидкости будут разными и лежат в интервале от нуля (для слоя прилипшего к стенкам трубы) до _max (для слоя, который движется по оси этой трубы (см. диаграмму распределения скоростей рис.1).

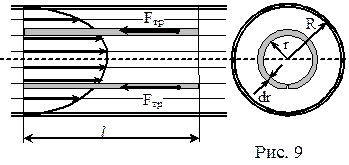
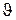
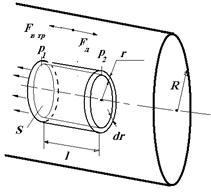
Выделим в потоке цилиндрический слой длиной l, радиусом r и толщиной dr (рис. 9). Радиус r будем измерять от осевой линии к периферии. Понятно, что слои примыкающие к неподвижным стенкам трубы будут течь медленнее, чем жидкость в середине потока. В силу этого, внутреннее трение, действующее на боковую поверхность выделенного слоя, будет равно:

, (9)

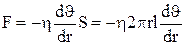
где S = 2πrl – боковая поверхность цилиндрического слоя, dυ/dr – градиент скорости в области поверхности соприкосновения цилиндра с внешними более медленными слоями жидкости. Знак минус означает, что при возрастании радиуса слоя его скорость уменьшается. Для установившегося течения сила внутреннего трения, действующая на боковую поверхность цилиндра, уравновешивается силами давления, действующими на его основания: F_тр = F_р или

, откуда . (10)

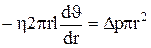
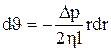
Полагая, что у стенок (на расстоянии R от оси) имеет место полное прилипание жидкости, т.е. скорость равна нулю, получим для выделенного слоя:

. (11)

Из (11) видно, что скорости частиц жидкости распределены по параболическому закону, причем вершина параболы лежит на оси трубы (рис. ).

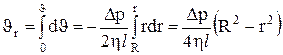
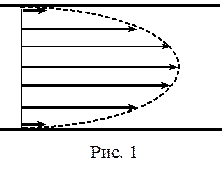
Объем жидкости, протекающей через поперечное сечение трубы за 1 с (расход жидкости, объёмная скорость течения) будет определяться соотношением:

. (12)

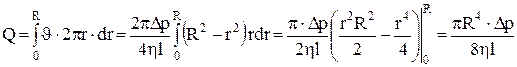
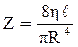
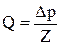
Это выражение была установлено эмпирически Гагеном (1839 г.) и Пуазейлем (1840 г.) независимо друг от друга и носит название формулы Пуазейля. Величина в формуле (10) называется гидравлическим сопротивлением сосуда. По аналогии с законом Ома (12) можно переписать в виде:

, (13)

где Δр играет роль напряжения, Q – силы тока, а Z – сопротивления.

Границы применимости формулы Пуазейля: 1) ламинарное течение; 2) гомогенная жидкость; 3) прямые жесткие трубки; 4) удаление от источников возмущений (изгибов, сужений, входа, выхода и т.д.).

Формула Пуазейля (12) лежит в основе многих методов определения вязкости жидкостей.

Источник