python номер числа фибоначчи
Числа Фибоначчи
Ряд чисел Фибоначчи представляет собой последовательность. Первый и второй элементы последовательности равны единице. Каждый последующий элемент равен сумме двух предыдущих. Рассмотрим разные способы нахождения элементов по номеру и генерацию списка с помощью Python 3.
Введение
Расчет ряда чисел Фибонначчи – один из лучших примеров программ на Python, использующих рекурсию. Хотя наиболее частый пример, рекурсии – это расчет факториала.
Рассмотрим варианты получения ряда Фибоначчи на Python 3:
Также сгенерируем список чисел и создадим генератор с помощью которого можно поочередно получать числа.
Если же запросят 3-ий или какой либо последующий элемент последовательности Фибоначчи, то мы зайдем в цикл. Во временную переменную tmp сохраним следующее число последовательности. После этого заполним prew и cur новыми значениям. Когда пройдет нужное количество итераций, выведем значение cur в консоль.
Теперь вместо трех строк кода получилась одна строка! И пропала необходимость использования дополнительной переменной.
Рекурсия
Конечно, пример с рекурсией интересен. Но он будет работать гораздо медленнее.
А если вы решите вычислить, допустим 1000-ый элемент последовательности. Используя цикл, мы его очень быстро рассчитаем. А вот в случае с рекурсией получим ошибку превышения максимального количества рекурсий:
Генератор списка
Если мы захотим инициализировать список рядом Фибоначчи, то это можно сделать следующим образом:
Если нам надо будет поочередно получать числа ряда, а не держать в памяти сразу весь список, то можно поступить следующим образом:
Здесь мы создали с помощью Python 3 генератор чисел Фибоначчи. При помощи функции next мы получаем поочередно числа ряда.
Определить номер числа Фибоначчи значение которого равно заданному числу
Вотм мой код, но он не верный.
Помощь в написании контрольных, курсовых и дипломных работ здесь.

Дано вещественное число А и массив Х(10). Определить номер элемента, равного числу А. Если такого.
Определить номер последнего элемента, значение которого равно 7.
Определить номер последнего элемента, значение которого равно 7.

Определить первый номер элемента массива С, значение которого равно Р
Решение
Black Fregat, плавающая точка в целочисленной задаче.
Добавлено через 15 минут
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Найти номер первого числа Фибоначчи, значение которого превышает 100
Найти номер первого числа Фибоначчи, значение которого превышает 100. Очень буду благодарна.
Присвоить переменной К номер элемента массива, равно заданному числу.
Задан массив целых чисел X, упорядоченный по возрастанию, а также целое число Y. Присвоить.

Определить номер элемента массива A$, значение которого равно значению заданной символьной.
Определить номер элемента списка, значение которого равно сумме первого и последнего элементов
Как реализовать данную задачу на Prolog? Определять номер элемента списка из целых чисел, значение.
Как вычислить миллионное число Фибоначчи на Python
Как-то раз я захотел найти оптимальное решение для вычисления чисел Фибоначчи и решил попробовать вычислить стотысячное число в последовательности, а потом подумал: если бы я мог вычислить стотысячное, то почему бы не вычислить миллионное число? Поэтому сейчас я покажу, как у меня это получилось и с какими проблемами я столкнулся.
Последовательность Фибоначчи является одной из наиболее известных математических последовательностей и самым простым примером рекурсий. Каждое число последовательности состоит из суммы двух предыдущих, где начальными числами выступают 0 и 1. Выглядит это всё вот так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так до бесконечности…
В течение следующих нескольких минут я пройдусь по нескольким различным подходам, а затем покажу оптимальное решение задачи:
1. Простая рекурсия.
2. Использование кэша с рекурсией.
3. Итеративный метод.
4. Использование формулы Бине.
5. Вычисление миллионного числа.
Перед тем как начать, нужно отметить, что все упомянутые замеры времени основаны именно на моем оборудовании и на версии Python 3.9.1.
1. Простая рекурсия
Это очень простой способ вычислить n-ное число Фибоначчи в Python:
Этот метод использует рекурсию, чтобы многократно вызывать функцию вычисления, рассчитывая предыдущее число и применяя его для вычисления следующего. Однако это и является недостатком метода, так как эта функция крайне неэффективная и ресурсоёмкая, ведь на каждой стадии она вычисляет два предыдущих числа, потом два предыдущих числа этого числа и так далее. В какой-то момент вы заметите, что вычисление одного числа будет занимать слишком много времени. На моем компьютере, например, вычисление 35-го числа Фибоначчи заняло 1,43 секунды. Поэтому очевидно, что вычисление еще больших значений стало бы невероятно медленным либо вообще практически невыполнимым.
2. Использование кэша с рекурсией
Поскольку мы постоянно вычисляем предыдущие два числа, то мы также можем использовать возможности кэширования для хранения числа, чтобы нам больше не нужно было их вычислять. Встроенный модуль functools позволяет нам использовать метод вытеснения из кэша (least recently used cache) — тип кэша, при котором все элементы в нем упорядочиваются по мере использования. Этот метод может значительно ускорить процесс.
Теперь, чтобы вычислить тысячное число Фибоначчи, требуется лишь 0,001198 секунд. Однако с этим методом у меня случилась еще одна проблема, потому что по какой-то неведомой причине я так и не смог вычислить 1553-е число в последовательности, и даже после увеличения глубины рекурсии ничего не помогло: терминал переставал выдавать число и просто завершал работу программы. Это, очевидно, проблема и недостаток на пути к вычислению миллионного числа Фибоначчи.
3. Итеративный метод
Можно заметить, что в среде программистов использование рекурсивного метода решения проблемы часто рассматривается как плохая практика, гораздо лучше считаются итеративные методы вычисления. Мы также можем придумать итеративное решение для генерации чисел Фибоначчи:
Этот метод можно использовать для вычисления любого числа Фибоначчи (однако я не проверял его на огромных числах), что также происходит очень быстро, так как всего за 0.0028195 я смог вычислить десятитысячное число Фибоначчи. И если подумать, почему бы не использовать этот метод для вычисления миллионного числа: это возможно, однако займет какое-то время перед тем как полностью загрузиться. Читайте дальше, и я расскажу, почему так происходит.
4. Формула Бине
Формула Бине — это формула, которую можно использовать для вычисления n-ного числа последовательности Фибоначчи, а это как раз то, что нам нужно. Эта формула названа в честь французского математика Жака Филиппа Мари Бине. Вот как она выглядит:
Фи (φ) равна золотому сечению:
Эту формулу мы можем использовать, если перенести ее в Python:
Эту проблему можно очень легко решить с помощью встроенного модуля Decimal, чтобы создать десятичный объект с гораздо большей точностью и размером для использования в нашем уравнении:
В этой новой функции мы устанавливаем значение точности до 10000 цифр и преобразуем значение корня из 5 в десятичный объект, а затем используем его в нашем уравнении. Такой способ позволяет нам легко вычислить десятитысячное число последовательности за невероятные 0,0692986 секунд, что является огромным улучшением по сравнению со всеми предыдущими методами.
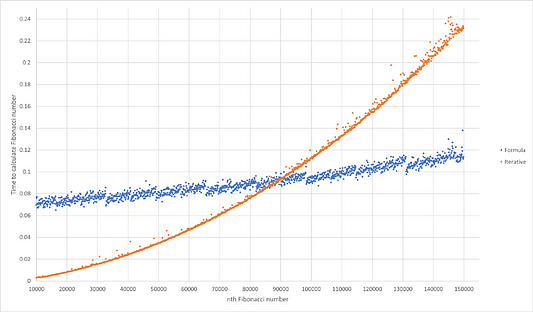
5. Вычисление миллионного числа
Как вы, возможно, заметили, применение формулы работает значительно медленнее итеративного метода, если n = 10000. Это связано с тем, что в формуле нам нужно создавать десятичный объект и использовать его в уравнении, а это занимает больше времени, чем повторение одного и того же действия 10000 раз. Однако это еще не конец истории.
Если увеличить количество повторений, необходимых для выполнения цикла, то это может значительно увеличить время завершения всего процесса. В какой-то момент, когда n достигает примерно 89200, время расчета при итеративном методе становится равным времени вычисления по формуле, а когда n увеличивается еще больше, то время итеративного метода увеличивается больше, чем по сравнению с увеличением времени по формуле.
На моем компьютере (а у вас это время может быть другим) вычисление миллионного числа Фибоначчи заняло:
Если вам хочется увидеть само число, оно состоит из 208988 цифр и в виде текстового файла весит 209 Кб:
Заключение
Вот так я и вычислил миллионное число Фибоначчи. Да, конечно, можно было вычислить число и побольше, но на самом деле это не имеет практического смысла, да и заняло бы много времени даже с применением формулы Бине. Из графика выше можно прикинуть, что на вычисление миллиардного числа Фибоначчи потребуется 310,8467 секунд. Оставлю эти расчёты на ваше усмотрение.
Серия Фибоначчи в Python и программа чисел Фибоначчи
Серия Фибоначчи в Python и программа чисел Фибоначчи
Что такое ряд Фибоначчи?
Согласно Google Ряд Фибоначчи это ряд чисел
в которой каждое число (число Фибоначчи) является суммой двух предыдущих чисел. Самым простым является ряд 1, 1, 2, 3, 5, 8, и т. д.
Последовательность Фибоначчи – это ряд чисел:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
Следующее число можно найти, сложив два числа перед ним.
Вот более длинный список:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, …
Можете ли вы вычислить следующие несколько чисел?
История
Последовательность Фибоначчи появляется в href=”https://en.wikipedia.org/wiki/Indian_mathematics”>Индийская математика в связи с href=”https://en.wikipedia.org/wiki/Sanskrit_prosody”>Санскритская просодия, как указал Пармананд Сингх в 1985 году. href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-HistoriaMathematica-8″>[8] [10] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-FOOTNOTELivio2003197-11″>[11] В санскритской поэтической традиции существовал интерес к перечислению всех образцов длинных (L) слогов длительностью 2 единицы, сопоставляемых с короткими (S) слогами длительностью 1 единица. Подсчет различных паттернов последовательных земель с заданной общей длительностью приводит к числам Фибоначчи: число паттернов длительности m единиц равно Fm + 1. href=”https://en.wikipedia.org/href=”https://en.wikipedia.org/wiki/Indian_mathematics”>Индийская математика в связи с href=”https://en.wikipedia.org/wiki/Sanskrit_prosody”>Санскритская просодия, как указал Пармананд Сингх в 1985 году. href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-HistoriaMathematica-8″>[8] [10] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-FOOTNOTELivio2003197-11″>[11] В санскритской поэтической традиции существовал интерес к перечислению всех образцов длинных (L) слогов длительностью 2 единицы, сопоставляемых с короткими (S) слогами длительностью 1 единица. Подсчет различных паттернов последовательных земель с заданной общей длительностью приводит к числам Фибоначчи: число паттернов длительности m единиц равно Fm + 1. href=”https://en.wikipedia.org/href=”https://en.wikipedia.org/wiki/Sanskrit_prosody”>Санскритская просодия, как указал Пармананд Сингх в 1985 году. href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-HistoriaMathematica-8″>[8] [10] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-FOOTNOTELivio2003197-11″>[11] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-FOOTNOTELivio2003197-11″>[11] В санскритской поэтической традиции существовал интерес к перечислению всех образцов длинных (L) слогов длительностью 2 единицы, сопоставляемых с короткими (S) слогами длительностью 1 единица. Подсчет различных паттернов последовательных земель с заданной общей длительностью приводит к числам Фибоначчи: число паттернов длительности m единиц равно Fm + 1. href=”https://en.wikipedia.org/href=”https://en.wikipedia.org/
Знание последовательности Фибоначчи было выражено еще в href=”https://en.wikipedia.org/wiki/Pingala”>Пингала (c. 450 до н. э.–200 до н. э.). Сингх цитирует загадочную формулу Пингалы misrau cha (“два смешаны”) и ученых, которые интерпретируют ее в контексте как говорящую, что число паттернов для m ударов (Fm+1) получается путем добавления одного [S] к F mслучаев и одного [L] кF случаев./em>m-1 случаев. href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-12″>[12] href=”https://en.wikipedia.org/wiki/Bharata_Muni”>Бхарата Муни также выражает знание последовательности в href=”https://en.wikipedia.org/wiki/Natya_Shastra”>Натья Шастра (около 100 г. до н. э.–около 350 г. н. э.). href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-13″>[13] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-GlobalScience-7″>[7] href=”https://en.wikipedia.org/wiki/Pingala”>Пингала (c. 450 до н. э.–200 до н. э.). Сингх цитирует загадочную формулу Пингалы misrau cha (“два смешаны”) и ученых, которые интерпретируют ее в контексте как говорящую, что число паттернов для m ударов (Fm+1) получается путем добавления одного [S] к F mслучаев и одного [L] кF случаев./em>m-1 случаев. href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-12″>[12] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-12″>[12] href=”https://en.wikipedia.org/wiki/Bharata_Muni”>Бхарата Муни также выражает знание последовательности в href=”https://en.wikipedia.org/wiki/Natya_Shastra”>Натья Шастра (около 100 г. до н. э.–около 350 г. н. э.). href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-13″>[13] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-GlobalScience-7″>[7] href=”https://en.wikipedia.org/wiki/Bharata_Muni”>Бхарата Муни также выражает знание последовательности в href=”https://en.wikipedia.org/wiki/Natya_Shastra”>Натья Шастра href=”https://en.wikipedia.org/wiki/Natya_Shastra”>Натья Шастра (около 100 г. до н. э.–около 350 г. н. э.). href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-13″>[13] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-GlobalScience-7″>[7] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-13″>[13] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-GlobalScience-7″>[7] href=”https://en.wikipedia.org/wiki/Fibonacci_number#cite_note-GlobalScience-7″>[7]
О Человеке Фибоначчи
Его настоящее имя было Леонардо Пизано Биголло, и он жил между 1170 и 1250 годами в Италии.
“Фибоначчи” было его прозвищем, что примерно означает “Сын Боначчи”.
Помимо того, что он прославился последовательностью Фибоначчи, он помог распространить индуистско-арабские цифры (как наши нынешние числа 0,1,2,3,4,5,6,7,8,9) по всей Европе вместо римских цифр (I, II, III, IV, V и т. Д.). Это избавило нас всех от многих неприятностей! Спасибо, Леонардо.
Читайте Также: Как Instagram Использует Django И Python
День Фибоначчи
День Фибоначчи-23 ноября, так как он имеет цифры “1, 1, 2, 3”, которые являются частью последовательности. Так что в следующем году, 23 ноября, пусть все знают!
Правило для рядов Фибоначчи
Последовательность Фибоначчи может быть записана как “Правило”
Во-первых, термины нумеруются от 0 и далее следующим образом:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | … |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | … |
Таким образом, термин номер 6 называется x6 (что равно 8).
| Пример: 8-й член-это 7-й член плюс 6-й 7 + x6 |
Так что мы можем написать правило:
Правило таково:n-1 + xn-2
Программа Python для рядов/Последовательностей Фибоначчи
Программа Python для рядов Фибоначчи с использованием итерационного подхода
Этот подход основан на следующем алгоритме1. Объявите две переменные, представляющие два члена ряда. Инициализируйте их в 0 и 1 как первый и второй члены ряда соответственно. Инициализируйте переменную, представляющую счетчик циклов, равным 0.3. Цикл от 0 до общего числа членов в ряду.4. На каждой итерации Добавьте переменные, определенные на шаге 1. Это представляет собой член(или элемент) ряда Фибоначчи. назначьте значение второй переменной первой, а сумму на вышеприведенном шаге А второй переменной.Итак, Python Программа для генерации рядов Фибоначчи написана в соответствии с приведенным выше алгоритмом следующим образом.
Таким образом, выход выполнения:
Введите, сколько чисел необходимо в ряду Фибоначчи –60,1,1,2,3,5,
Программа Python для рядов Фибоначчи с использованием рекурсии
Создайте рекурсивную функцию, которая получает целое число в качестве аргумента. Этот целочисленный аргумент представляет позицию в ряду Фибоначчи и возвращает значение в этой позиции. Таким образом, если он получает 5, то возвращает значение в 5-й позиции в ряду Фибоначчи. Эта рекурсивная функция возвращает 0 и 1, если значение аргумента равно 0 или 1. Для всех остальных значений он называет себя суммой n-й и (n-1) – й позиций.Программа считывает с клавиатуры общее количество элементов в рядах Фибоначчи. Затем он инициирует цикл, начинающийся с 0 до этого входного значения. На каждой итерации вызывается рекурсивная функция и выводится результирующий элемент Фибоначчи для этой позиции.
Таким образом, выход вышеприведенного исполнения является
Применение ряда Фибоначчи/последовательности/числа
Итак, я надеюсь, что вам понравилась эта статья, и если у вас есть какие-либо вопросы/рекомендации или вы просто хотите сказать привет, прокомментируйте ниже!
Фибоначчи Поиск в Python [с легким примером]
Поиск FIBONACCI – это еще один алгоритм деления и завоевания, который используется для поиска элемента в данном списке. В этом руководстве мы увидим, как это работает, как это
Фибоначчи Поиск в Python [с легким примером]
Поиск FIBONACCI – это еще один алгоритм деления и завоевания, который используется для поиска элемента в данном списке. В этом руководстве мы увидим, как это работает, как он отличается от бинарного поиска, и мы будем реализовать его в Python.
Предпосылки
Есть две темы, которые нам нужно сначала понять, прежде чем перейти на поиск Fibonacci.
1. Бинарный поиск
Двоичный поиск – это алгоритм деления и завоевания, что означает, что мы разделяем наш список, чтобы найти наш ответ. Данный список должен быть отсортирован так, чтобы мы могли выполнить алгоритм.
Мы смотрим на средний элемент списка, и потому что список сортируется, мы узнаем, где цель относительно среднего элемента. Мы либо найдем цель в середине списка, или мы устраним одну сторону с середины в зависимости от того, меньше или больше, чем средний элемент. После устранения одной стороны мы повторяем этот процесс с другой стороны.
Таким образом, в каждой итерации мы сократили половину нашего списка, чтобы найти N элементов, нам нужно только журнал 2 и итерации.
2. Фибоначчи
Числа Фибоначчи – это цифры, которые образуют серию Fibonacci. Итак, давайте сначала определим сериал Фибоначчи. Мы можем определить сериал рекурсивно, как:
У нас есть прямой способ получения чисел Фибоначчи через формулу, которая включает в себя экспоненты и золотое соотношение, но таким образом, это как серия предназначена для воспринимаемого.
В вышеуказанном определении F (N) означает «NTH FIBONACCI номер».
Таким образом, число 0-го фибоначчи 0, число 1-го фибоначчи составляет 1, 2-й номер Fibonacci – это сумма чисел 1-й и 0-го фибоначчи, номер 3-го фибоначчи является суммой 2-го и 1-го числа фибоначчи и так далее.
Наконец, номер NTH FIBONACCI – это сумма двух чисел фибоначчи до нее, то есть сумма (N-1) Th и (N-2) чисел Фибоначчи.
Вот расчет первых 10 чисел фибоначчи.
Итак, серия Fibonacci, начиная с 0-го:
F, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Реализация поиска фибоначчи в Python
Подобно бинарному поиску, поиск Fibonacci также является алгоритмом разделения и завоевания и нуждается в отсортированном списке. Он также делит список на две части, проверяет цель с элементом в центре двух частей и устраняет одну сторону на основе сравнения. Так как именно это отличается от бинарного поиска?
В поисках Fibonacci мы используем номера Фибоначчи для разделения списка на две части, поэтому он будет разделить список на две части разных длин. Кроме того, вместо того, чтобы исполнять деление, чтобы сделать это, он выполняет дополнение, которое меньше налога на ЦП. Теперь давайте погрузимся в детали.
Во-первых, нам нужно иметь длину данного списка. Затем мы находим наименьшее число фибоначчи, больше или равно размеру списка. Это означает, что если размер списка составляет 100, то наименьшее число Fibonacci больше 100 составляет 144. Давайте скажем, что это число NTH FIBONACCI. В приведенном выше примере 144 – 12-й номер фибоначчи.
После этого мы переходим в два раза в серии Фибоначчи из этого числа. По сути, мы находим (N-2) Th Fibonacci номер. Таким образом, в приведенном выше примере мы нашли 12-й номер Фибоначчи, который составляет 144, поэтому нам нужно 10-й, который составляет 55.
Мы используем это в качестве индекса для разделения списка на две части. То есть мы смотрим на этот индекс в списке, и при условии, что список отсортирован в увеличении порядка, если элемент на этом индексе меньше, чем цель, то мы устраняем левую сторону, в противном случае мы устраняем правую сторону. Мы делаем это, пока мы не найдем товар, который мы ищем, который произойдет, когда предмет рассчитанного индекса будет соответствовать цели.
Теперь давайте погрузимся в код для этого алгоритма:
Теперь давайте попробуем запустить его и увидеть его вывод:
Заключение
В этом руководстве мы обсудили, какие номера фибоначчи являются, как они используются в алгоритме поиска фибоначчи, как работает алгоритм, и мы реализовали алгоритм в Python. Надеюсь, у вас было отличное время обучения, и увидимся в следующем уроке.