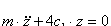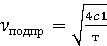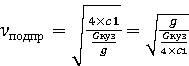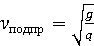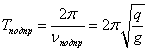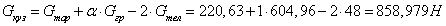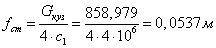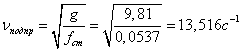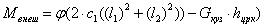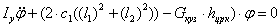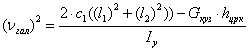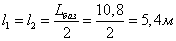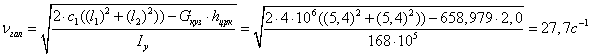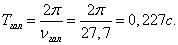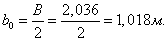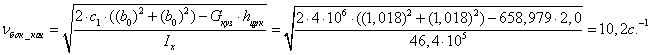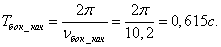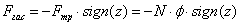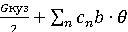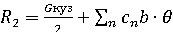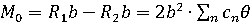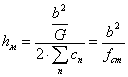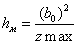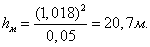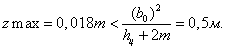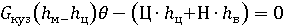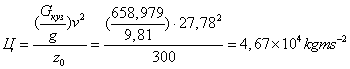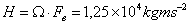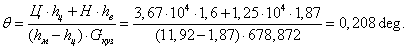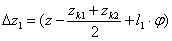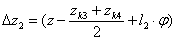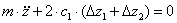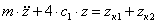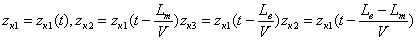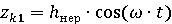галопирование вагона что это

Виды колебания кузова вагона

Во время движения по рельсовому пути кузов вагона испытывает сложные колебательные движения. Эти колебания возбуждаются динамическими усилиями и обусловливаются неровностями пути, наличием зазоров на стыковых рельсовых соединениях, коничностью поверхности катания колесных пар, а также наличием неровностей на этой поверхности, непостоянством физических свойств материалов пути и колесных пар, типом рессорного подвешивания, изменением скорости вагона и друрими.

Рессорное подвешивание и гасители колебаний, применяемые в вагонах, уменьшают влияние динамических усилий и обеспечивают более плавное движение вагона. Однако действие этих усилий (вертикальных, поперечных и продольных) настолько существенно, что обрессоренные массы вагонов приходят в колебательное состояние.

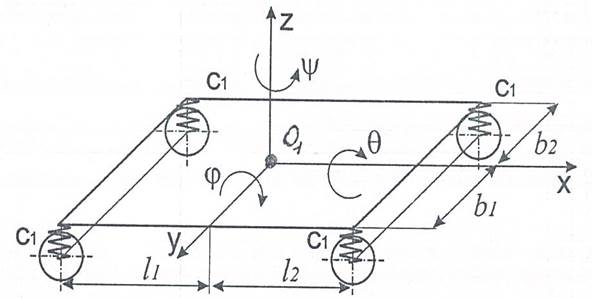
При изучении колебаний кузова вагона он рассматривается в пространственной системе координат (рис. 1, а) как твердое тело. Под влиянием действующих на вагон сил могут возникать следующие виды главных колебаний.

Рис. 1 – Главные виды колебаний

Подпрыгивание, когда обрессоренные части вагона перемещаются вверх и вниз параллельно первоначальному положению по оси z–z на величину ±z (рис. 1, б), возникает под действием вертикальных динамических сил, вызывающих одинаковые ускорения по концам кузова.

Продольная качка или галопирование – обрессоренные части вагона совершают вращательное движение относительно оси у–у на некоторый угол ±θ (рис. 1, в) – возникает от ударов колес на стыках, наличия выбоин на одной колесной паре или от неуравновешенности кузова. Галопирование вагона обычно возникает одновременно с подпрыгиванием.

Колебания поперечного относа – кузов и тележка вагона перемещаются вдоль оси у–у (рис. 1, г). Этот вид колебаний возникает совместно с колебаниями боковой качки (рис. 1, д) под действием горизонтальных боковых сил, параллельных оси.

Виляние, когда кузов вращается вокруг вертикальной оси на некоторый угол ±ψ (рис. 1, е), вызывается коничностью поверхности катания колес, неправильной установкой колесных пар, неодинаковой величиной диаметра колес, извилистостью пути.

Подергивание (рис. 1, ж) – перемещение вагона вдоль оси х–х. Оно появляется при трогании поезда с места, торможении вследствие неуравновешенности поступательно движущихся масс локомотива.

Названные колебания могут проявляться отдельно и совместно с другими видами, поэтому вагон совершает сложное движение. Зная причины появления колебаний и их характер, можно определить условия устойчивого и безопасного движения вагона, подобрать рациональные параметры его рессорного подвешивания и поглощающих аппаратов автосцепного устройства. К динамическим характеристикам вагона относятся периоды различных видов колебаний, коэффициенты динамики и критические скорости. В динамике вагонов различают собственные колебания, которые происходят от начального толчка без воздействия в дальнейшем на надрессорное строение каких-либо внешних сил, и вынужденные колебания, возникающие под влиянием периодически меняющейся силы, которую обычно называют возмущающей.

Частота собственных колебаний υc зависит от массы надрессорных частей вагона и жесткости рессорного подвешивания. Частота вынужденных колебаний υв, равна частоте изменений возмущающей силы.

При равенстве частот υв и υc, т. е. при υв:υc = 1, амплитуда колебаний значительно возрастает, наступает явлениерезонанса колебаний, т. е. совпадение периодов свободных колебаний с периодом проявления возмущающей силы. Явление резонанса колебаний характеризуется большими амплитудами или, если применяются ограничивающие колебания устройства, чрезмерно большими силами.Эти силы и перемещения вызывают повышенный износ, а также поломки деталей вагонов и угрожают безопасности движения. Явление резонанса происходит при определенной скорости, которая называется критической. Для гашения колебаний и предотвращения явлений резонанса предусматривается рессорное подвешивание с необходимой величиной коэффициента относительного трения, при которой обеспечивается условие ненарастания колебаний.

где φ – коэффициент относительного трения в рессорном подвешивании;

fст – статический прогиб рессорного подвешивания;

Источник

Галопирующие колебания вагона

Галопирующие колебания – это вращательные колебания вокруг горизонтальной оси Y, перпендикулярной бортам вагона и проходящей через центр масс вагона. При этом движение вагона подобно галопу лошади. Колебания обусловлены упругими силами подвески и инертностью вагона.

Пусть из-за случайного толчка, например на стыке рельсов или при падении груза, корпус вагона наклонился. Пусть при этом пружины передней вагонной тележки сжались, а задней тележки – растянулись. Возникает момент упругих сил пружин подвески, стремящийся вернуть вагон в положение равновесия. Но вагон по инерции проходит положение равновесия, поворачиваясь в противоположном направлении. Потом движение повторяется в обратном направлении, и таким образом возникают галопирующие колебания.

Определим период галопирующих колебаний. Так как это вращательные колебания, то для вывода применим основной закон динамики вращательного движения: произведение момента инерции вагона относительно оси вращения на угловое ускорение равно моменту упругих сил подвески: J ε = М.

Получим формулу для момента силы, который создают пружины подвески. По закону Гука упругие силы пружин пропорциональны деформации пружин и направлены противоположно деформации F = –kx. Так как передняя подвеска сжата, то ее сила упругости направлена вертикально вверх, а сила упругости растянутой задней подвески – вниз (рис. 14.4). Момент пары упругих сил подвески F равен произведению силы на плечо пары сил: M = F l, где плечо l равно расстоянию между линиями действия сил, то есть между серединами передней и задней вагонных тележек. Деформация пружин х связана с углом поворота вагона как длина дуги с центральным углом: 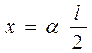. 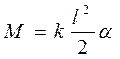Итак, момент упругих сил, действующий на вагон, равен

.

Подставив в закон динамики вращательного движения формулу момента силы, получим дифференциальное уравнение галопирующих колебаний 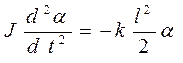. (14.14)

Здесь угловое ускорение записано как вторая производная от угла поворота по времени. Решением этого дифференциального уравнения должна быть функция, у которой вторая производная имеет такой же вид, как и сама функция, но противоположного знака. Например, это может быть функция косинуса

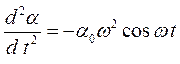
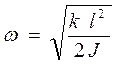
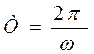
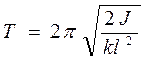
где α₀ – амплитуда колебаний, ω – циклическая частота колебаний. Если определить вторую производную от угла поворота по времени и подставить в дифференциальное уравнение, то выбранная функция будет решением, при условии, если циклическая частота колебаний равна . Период колебаний будет равен

. (14.16)

Здесь k –– коэффициент упругости пружин подвески, принятый одинаковым для передней и задней вагонных тележек, J – момент инерции вагона.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

9.8 Взаимодействие вагонов и пути

Взаимодействие вагонов и пути — одна из основных научных технических дисциплин железнодорожного транспорта, имеющая большое практическое значение. Основные объекты исследований этой дисциплины — конструкции пути и вагонов и параметры этих конструкций.

Изучение процессов взаимодействия вагонов и пути началось вместе с зарождением железнодорожного транспорта, поскольку результаты исследований их взаимодействия необходимы для создания надежных и долговечных конструкций вагонов и пути, определения норм их устройства, правил ремонта и технического содержания. Дисциплина включает в себя исследования плоских и пространственных колебаний вагонов при движении их по детерминированным и случайным (стохастическим) неровностям пути; деформаций и необходимых конструктивных размеров элементов вагонов и пути с целью обеспечения достаточной прочности, долговечности, надежности в эксплуатации.

Изучение процессов взаимодействия вагонов и пути началось вместе с зарождением железнодорожного транспорта, поскольку результаты исследований их взаимодействия необходимы для создания надежных и долговечных конструкций вагонов и пути, определения норм их устройства, правил ремонта и технического содержания. Дисциплина включает в себя исследования плоских и пространственных колебаний вагонов при движении их по детерминированным и случайным (стохастическим) неровностям пути; деформаций и необходимых конструктивных размеров элементов вагонов и пути с целью обеспечения достаточной прочности, долговечности, надежности в эксплуатации.

Исследования взаимодействия вагонов и пути являются научной базой рационального конструирования и эксплуатации вагонов и железнодорожного пути и средством интенсификации их использования, повышения пропускной и провозной способности железных дорог, обеспечения безопасности движения с точки зрения устойчивости колеса на рельсе и устойчивости от поперечного опрокидывания кузова вагона в кривых. Для выбора рациональных параметров вагонов при их проектировании, разработки норм размещения перевозимых грузов в вагонах; решения вопросов безопасности движения и повышения прочности и надежности узлов вагонов; определения конструктивной скорости движения вагонов; уменьшения силового воздействия вагонов на путь; обеспечения плавности хода, в частности пассажирских вагонов; уменьшения механического воздействия на перевозимые в грузовых вагонах грузы и соблюдения требований ездового комфорта пассажиров необходимо правильно и точно описать качественно и количественно динамические процессы, происходящие в движущемся вагоне, и управлять этими процессами.

Эту часть дисциплины о взаимодействии вагонов и пути, в которой сконцентрирована совокупность методов и приемов решения задач по качественному и количественному описанию динамических процессов в вагоне и рекомендаций по улучшению динамических показателей вагонов, называют динамикой вагона.

При проектировании конструкций железнодорожного пути и его элементов с выбором их геометрических форм, показателей прочности и надежности, с определением наибольших скоростей движения вагонов и их осевых нагрузок; норм устройства и содержания пути используется совокупность знаний, которая называется динамикой железнодорожного пути и теорией его проектирования и эксплуатации.

Основой обоих направлений взаимодействия вагонов и пути является область исследований или расчетов, которая рассматривает вагон и путь как единую механическую систему. После решения вопросов в общем плане в ряде случаев удается рассматривать изолированно с известной мерой допущения вопросы теоретической механики, относящиеся к вагону или к пути.

Наука о взаимодействии вагонов и пути служит для обеспечения безопасной перевозки грузов и пассажиров в кратчайшие сроки с минимальными затратами материалов на создание и эксплуатацию вагонов. Обеспечение безопасности движения поездов, надежности работы вагонов и пути с их максимальной производительностью и с минимальными затратами труда и энергии, особенно при высоких скоростях движения (свыше 250 км/ч для пассажирских поездов), осевых нагрузках до 30 т и погонных нагрузках до 10—12 т/м для грузовых поездов, при грузонапряженности отдельных линий свыше 200 млн т-км брутто в год, не может быть осуществлено без знания процессов взаимодействия пути и вагонов, которые в конечном итоге сводятся к взаимосвязанным случайным колебаниям различных элементов вагонов и пути, при которых могут возникнуть значительные остаточные деформации пути или потеря устойчивости вагонов на рельсах, усталостные или хрупкие поломки элементов или деталей вагонов и пути. Поэтому умение прогнозировать и рассчитывать, в зависимости от конструктивных особенностей вагонов, скоростей движения, норм содержания пути и вагонов и отступлений от них, грузонапряженности и ряда других факторов, процессы случайных колебаний вагонов и их эволюцию по мере износа пути и вагонов во всех звеньях единой механической системы «вагон — путь», умение управлять этими процессами и составляет конечную цель науки о взаимодействии вагонов и пути.

При этом управление указанными процессами не предусматривает обязательного сведения их к нулю, поскольку это на практике невозможно. Нужно лишь стремиться свести их к такому разумному минимуму, который обеспечивает технические требования к данной системе с учетом перспективы ее эксплуатации и не требует чрезмерных затрат на ее создание и эксплуатацию.

В настоящее время многие важные для железнодорожного транспорта задачи науки о взаимодействии вагонов и пути уже решены или успешно решаются для большей части практических проблем с использованием современных достижений в механике, математике и кибернетике, что позволило в буквальном смысле провести революцию в этой научной дисциплине.При изучении процессов взаимодействия вагонов и пути исследуются колебания вагонов и пути и динамические силы, развивающиеся в единой динамической системе «вагон—путь». Для теоретического исследования колебаний вагона и пути принято строить такие расчетные схемы и модели, в которых этот сложный колебательный процесс разделен на отдельные составляющие его линейные колебания: вертикальные, поперечные и продольные горизонтальные. При этом следует принимать во внимание, что обрессоренная масса вагона (рама тележки, кузов с грузом) может совершать также и угловые колебания.

К вертикальным линейным колебаниям вагона относятся подпрыгивание и галопирование, а к горизонтальным поперечным колебаниям — виляние, боковая качка и поперечный относ кузова на рессорном подвешивании.

Подпрыгивание — это вертикальные одинаковые по величине в каждый момент времени поступательные перемещения всех точек вагона или его обрессоренной массы (кузов, рама тележки).

Галопирование — это вертикальные перемещения точек вагона, возникающие в результате поворота или вращения кузова вокруг мгновенной горизонтальной поперечной оси вращения, проходящей через центр массы вагона.

Виляние — это поперечные колебания колесных пар, совершающиеся в пределах зазоров между гребнями колес и внутренней гранью головок рельсов, приводящие к извилистому движению вдоль пути колесных пар тележек, кузова.

Колебания относа — это поперечные горизонтальные колебания, при которых в каждый момент времени возникают одинаковые по величине поступательные перемещения кузова или рамы тележки.

Боковая качка — это вращательные движения кузова вагона вокруг мгновенной продольной оси вагона. Горизонтальные продольные по отношению к оси пути колебания вагона называются подергиванием.

Изучение процесса взаимодействия пути и вагонов, а также выполнение инженерных расчетов и исследований сводится к следующему: выбор соответствующей математической модели процесса взаимодействия или его расчетной схемы, определение метода исследования и нахождение метода решения той или иной конкретной задачи, определение исходных данных для расчетов или исследований, т.е. параметров всех элементов, входящих в модель или расчетную схему.

Математическая модель представляет собою систему дифференциальных уравнений, выражающих условия динамического равновесия динамической системы «вагон-путь». По этим уравнениям определяют свойства динамической системы, в частности, ее амплитудно-частотную характеристику, с помощью которой при заданных функциях неровностей пути и неровностей на поверхности качения колес могут быть определены параметры колебаний обрессоренной и необрессоренной масс, которые используются на практике для определения напряженного состояния, прочности, надежности элементов вагона и пути, накопления в них остаточных деформаций, возможного схода вагона с рельсов, для установления допускаемой скорости движения вагона.

В экспериментальных исследованиях взаимодействия вагона и пути определяются механические характеристики вагона и пути, значения наиболее существенных параметров механических процессов во взаимодействующих конструкциях. В основу этих исследований положены комплексные испытания с использованием динамометрического и путеиспытательного вагонов-лабораторий, с помощью которых регистрируются соответствующей электронной измерительной аппаратурой и компьютерами линейные и угловые перемещения обрессоренных и необрессоренных масс вагона; вертикальные и горизонтальные ускорения и динамические силы, действующие на вагон при различной конструкции пути и различных неровностях пути; вертикальные и горизонтальные нагрузки на путь от вагонов, напряжения в элементах вагона и пути.

По результатам испытаний определяется максимально допустимая скорость движения вагонов по пути с различными типами верхнего строения и различным планам линии (прямые, кривые) при наличии различных отступлений от проектных норм устройства пути и ходовых частей вагона. В комплексных испытаниях изучается также влияние на динамические процессы различных вариантов конструктивных решений в ходовых частях вагона.

Источник

РАСЧЕТ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ВАГОНА

Страницы работы

Содержание работы

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Иркутский государственный университет путей сообщения»

Факультет транспортных систем

Кафедра «Вагоны и вагонное хозяйство»

РАСЧЕТ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ВАГОНА

студент гр. ПСЖ.2-14-1

1. Тара вагона 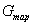= 220,63 кН;

2. Грузоподъемность 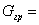604,96 кН;

3. База вагона 2L= 10800 мм;

4. Длина вагона 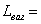13870 мм;

5. Площадь ветровой нагрузки F= 50;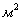

6. Высота центра давления ветровой нагрузки 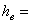2,2 м;

7. Высота центра вагона при полной загрузке относительно головки рельса 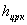=2,0 м;

8. Жесткость одного рессорного комплекта 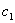= 4 МН/м;

9. Расстояние между клиньями автосцепок 2K= 11,87 м.

2. База тележки 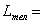1,85 м;

3. Вес тележки 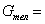4800 кгс;

5. Максимальный прогиб рессорного комплекта Zmax=50 мм;

6. Полярный момент инерции I0 = 0,625;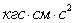

7. Тип гасителей колебаний – II тип.

1. Использование грузоподъемности вагона 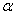=1 %;

2. Высота центра тяжести кузова с грузом hцрк=1,8 м;

3. Скорость движения вагона V=100 км/ч = 27,78 м/с;

4. Амплитуда неровности пути 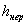= 0,6 м.

1.1 Составление дифференциальных уравнений собственных колебаний кузова на рессорах. Определение собственных частот колебаний подпрыгивания, галопирования и боковой качки вагона

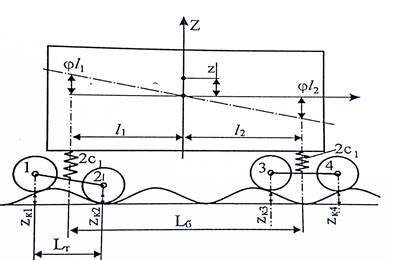
На рисунке 1 показано, что нагрузка передаётся на колёсные пары через рессоры и что жёсткость каждой рессоры вагона равна с1. Дальнейшее рассмотрение не изменилось бы, если бы вертикальные усилия от надрессорного строения передавались непосредственно на оси, а на надрессорные балки тележек, а те уже с помощью рессор передавали бы эти усилия тележкам. Важно то, что в каждой из четырёх точек усилия надрессорного строения передаются на тележки через одну рессору, т.е имеет место одинарное рессорное подвешивание. Частоты собственных колебаний с включением гасителя параллельно рессоре отличаются от собственных колебаний рессор без гасителей не более чем на 2%. Поэтому в целях упрощения, в дальнейшем рассмотрении собственных колебаний вагона исключим гасители колебаний, имеющихся во всех типах рессорного подвешивания в том или ином конструктивном оформлении. Представим, что масса надрессорного строения m в точке сосредоточена в точке О1, представляющий собой центр масс надрессорного строения вагона, а жёсткость каждой рессоры постоянна и равна С1. Поскольку масса при подпрыгивании совершает перемещения вдоль оси z и при этих же перемещениях все рессоры будут деформированы на величину z, то вполне очевидно отсутствие принципиального различия схемы колебаний подпрыгивания вагона и колебаний груза на пружине(системы с одной степенью свободы). Уравнение колебаний подпрыгивания, следовательно, можно записать в следующем виде

Здесь общая жёсткость рессорного подвешивания равна жёсткости четырёх рессор, т.е 4с1. Угловая частота собственных колебаний подпрыгивания равна

Поскольку 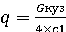, т.е статическому прогибу рессор,то

Соответственно период колебаний подпрыгивания

Вес кузова вагона определяются по формуле

1.2 Галопирование и боковая качка.

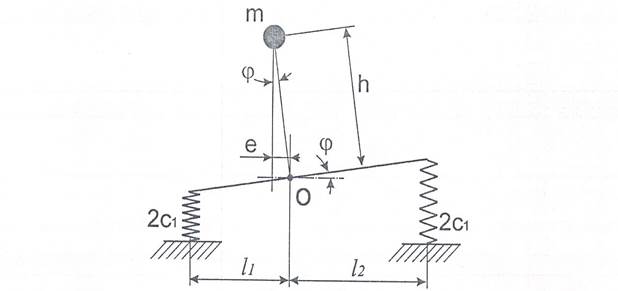
Для удобства рассмотрения колебаний галопирования схему вагона удобнее представить в плоскости xOz （рисунок 2）, однако рассмотрение колебаний галопирования по такой схеме корректно только в случае равенства расстояний l1=l2

Как известно из теоретической механики, момент сил инерции тела, вращающегося относительно оси у, равен 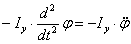, где Iy момент инерции тела (в данном случае кузова вагона) относительно оси у, а ᵩ«- угловое ускорение вращения кузова вокруг этой же оси.

По принципу Даламбера момент сил инерции кузова вагона всегда уравновешен моментом внешних сил Мвнеш, приложенных к кузову относительно его оси вращения т.е.

Iyφ«+ 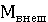= 0

Момент сил 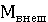относительно точки О образуется силами, возникающими в рессорном подвешивании, и силами тяжести кузова за счёт того, что его центр тяжести при повороте вокруг точки О смешается на величину е=h*φ

Получим известное уравнение( в данном случае колебаний галопирования), где νгал-угловая частота собственных колебаний галопирования кузова вагона

Из этой формулы следует, что чем меньше жёсткость рессорного подвешивания, чем больше момент инерции кузова и выше центр тяжести, тем меньше частота собственных колебаний галопирования, и тем больше период колебаний галопирования.

Период собственных колебаний галопирования кузова

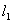
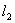
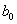
Колебания боковой качки могут быть рассмотрены с помощью той же схемы, приняв в ней вместо и величины и вместо момента инерции кузова вагона (относительно оси у)- момент инерции кузова относительно оси х- величину. Это позволяет написать формулы для определения частот и периода собственных колебаний боковой качки кузова вагона

1.4 Расчёты параметров гасителе

Возрастание колебаний при биениях, а особенно при резонансе, может привести к весьма опасным последствиям. Так в случае колебаний вагона при восходящем движении рессор возможна полная разгрузка колёсной пары от действия надрессорного строения и сход колёс с рельсов под воздействием боковых сил. При нисходящем движении рессор витки пружины рессорного подвешивая могут сомкнутся, путь и вагон при этом будет испытывать весьма большие удары, так как общая ударная масса будет равна сумме массы колеса и приходящейся на колесо массы кузова. Поэтому при конструировании вагонов принимают меры к снижению амплитуд колебаний путём установки гасителей колебаний. Для этого стремятся всю энергию, которая поступает в упругие элементы колебательной системы, израсходовать на трение в гасителях с тем, чтобы она превращалась в тепловую энергию и рассеивалась в окружающее пространство.

Гаситель с постоянной силой трения тип II

Где φ-коэффициент трения

1.5 Проверка отсутствия валкости кузова

Динамические силы, действующие на кузов, грузы или пассажиров, тем меньше, чем меньше, частоты собственных колебаний вагонов. Поэтому понижаем жесткость рессорного подвешивания.

Однако эту жесткость нельзя снижать ниже некоторых пределов. Для грузовых вагонов чрезмерное уменьшение жёсткости может привести к тому, что разница в высоте рамы порожнего и гружёного вагонов будет больше той, при которой возможна нормальная работа автосцепки. Кроме того, при чрезмерной мягкости рессор у грузовых вагонов они будут иметь недостаточную поперечную устойчивость, при которой наклон кузова под действием поперечных горизонтальных сил (центробежной силы Ц и силы ветра Н) может превосходить допустимые величины или же в результате наклона кузов не будет возвращаться в исходное положение, т.е, вагон будет обладать большой «валкостью».

=

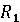
Момент реакций рессор относительно точки О1

Для того, чтобы кузов вагона после его наклона возвращался в вертикальное положение, необходимо, чтобы восстанавливающий момент был больше момента силы тяжести кузова вагона, т.е. чтобы было больше или высота метацентра была больше высоты центра масс вагона.

Отсюда ограничение статического прогиба

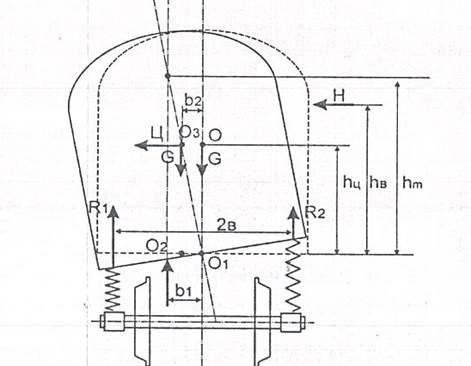
Определим величину наклона кузова на рессорах(крен кузова) под действием центробежной силы Ц и силы ветра Н. Равновесие кузова (без учёта динамических сил) показано на рисунке 3.

R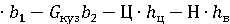=0

Из формулы следует, что при приближении hц к hм величина угла наклона кузова быстро растёт.

1.6 Составление дифференциального уравнения вынужденных колебаний подпрыгивания вагона при движении его по регулярным неровностям пути.

Зная деформации рессор и используя принцип Даламбера можем написать уравнение колебаний подпрыгивания

Учитывая, что l1=l2, то уравнение примет вид

Часто в качестве функции zk1 принимают волнообразные неровности пути вида

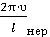
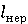
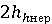
Где ω= ; здесь — расстояние между двумя горбами неровности, — глубина неровности пути, измеренная между двумя горбами, а ʋ-скорость движения вагона.

Федорова З.А., Котельникова Л.И. Расчет статических характеристик электродвигателей по паспортным данным: методические указания. – Иркутск: ИрГУПС, 2003. – 43 с.

Зорохович А.Е., Крылов С.С. Основы электротехники для локомотивных бригад: Учебник для техн. школ. – 2-е изд., перераб. и доп. – М.: Транспорт, 1987. – 414 с.: ил., табл.

Вольдек А.И. Электрические машины. Учебник для студентов высш. техн. учебн. заведений. – 3-е изд., перераб. – Л.: Энергия, 1978. – 832 с., ил.

Источник