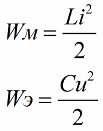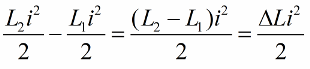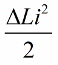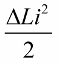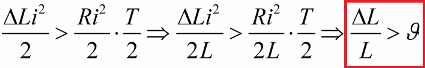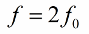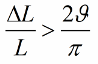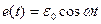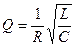Вопросы.

1. Могут ли свободные колебания быть незатухающими? Почему?

Свободные колебания не могут быть незатухающими, т.к. часть энергии всегда уходит на преодоление сил трения.

2. Что необходимо делать для того, чтобы колебания были незатухающими?

Для того чтобы колебания были незатухающими, необходимо восполнять потерю энергии, например прикладывая периодически к телу внешнюю силу.

3. Какие колебания называются вынужденными?

Вынужденными колебаниями называются колебания происходящие под действием внешней, периодически изменяющейся силы.

4. Что такое вынуждающая сила?

Вынуждающей силой называется внешняя, периодически изменяющаяся сила, вызывающая вынужденные колебания.

5. В каком случае говорят, что колебания установились?

Колебания установились, если амплитуда и частота вынужденных колебаний перестают изменяться.

6. Что можно сказать о частоте установившихся вынужденных колебаний и частоте вынуждающей силы?

Частота установившихся вынужденных колебаний и частота вынуждающей силы равны.

7. Могут ли тела, не являющиеся колебательными системами, совершать вынужденные колебания? Приведите примеры.

Вынужденные колебания совершают поршни в двигателе, швейная игла, мембрана звукового динамика, лопасти ветряной мельницы.

8. До каких пор происходят вынужденные колебания?

Вынужденные колебания происходят до тех пор, пока действует вынуждающая сила.

1. Рассмотрите рисунок 52 и скажите, какие из тел способны совершать: свободные колебания; вынужденные колебания. Ответ обоснуйте.

2. Могут ли происходить: а) вынужденные колебанияв колебательной системе; б) свободные колебания в системе, не являющейся колебательной? Приведите примеры.

а) да, такие колебания могут происходить, например раскачивание качелей или маятник часов; б) нет, такие колебания происходить не могут по определению.

Источник

Незатухающие колебания и параметрический резонанс

Незатухающие колебания — колебания, энергия которых с течением времени не изменяется. В реальных физических системах всегда существуют причины, вызывающие переход энергии колебаний в тепловую (например, трение в механических системах, активное сопротивление в электрических системах).

Поэтому незатухающие колебания можно получить только при условии, что эти потери энергии восполняются. Такое восполнение автоматически осуществляется в автоколебательных системах за счет энергии из внешнего источника. Электромагнитные незатухающие колебания используются чрезвычайно широко. Для их получения применяются различные генераторы.

Чтобы сделать электрические или механические колебания (колебательного контура или маятника) незатухающими, необходимо все время компенсировать потери на сопротивление или на трение.

Можно, например, воздействовать на колебательный контур переменной ЭДС, которая будет периодически увеличивать ток в катушке, и соответственно поддерживать амплитуду напряжения на конденсаторе. Или можно подталкивать маятник, аналогичным путем поддерживая его гармоническое качание.

Как известно, величина энергии магнитного поля катушки колебательного контура связана с ее индуктивностью и током следующим соотношением (вторая формула — энергия электрического поля конденсатора того же кобательного контура)

Из первой формулы ясно, что если мы будем периодически увеличивать ток в катушке, воздействуя на контур переменной ЭДС, то (увеличивая или уменьшая второй сомножитель в формуле — ток) станем периодически пополнять тот контур энергией.

Запишем это положение для единичного изменения индуктивности катушки:

Наиболее выразительным эффект раскачки контура получится в том случае, если изменения индуктивности осуществлять точно вовремя. Например, если взять все тот же контур в произвольный момент времени, когда по нему уже течет какой-то ток i, и внести в катушку сердечник, то энергия изменится на такую величину:

Теперь пусть свободные колебания происходят в контуре сами, но в момент времени, когда через четверть периода энергия полностью перешла в конденсатор и ток в катушке обратился в ноль, резко вынем сердечник из катушки. Индуктивность вернется к своему исходному состоянию, к первоначальной величине L. Работы против магнитного поля при выдвигании сердечника затрачивать не придется. Следовательно при вдвигании сердечника в катушку, контур получил энергию, ибо мы совершили работу, величина которой:

Через четверть периода конденсатор начинает разряжаться, его энергия снова переходит в энергию магнитного поля катушки. Когда магнитное поле достигнет амплитуды — снова резко вдвинем сердечник. Опять индуктивность увеличилась, приросла на ту же величину.

И вновь при нулевом токе возвращаем индуктивность к исходному значению. В итоге, если приросты энергии за каждые полпериода превосходят потери на сопротивление, энергия контура будет все время возрастать, амплитуда колебаний станет увеличиваться. Это положение выражается неравенством:

Здесь мы разделили обе части этого неравенства на L, и записали условие возможности параметрического возбуждения скачками для определенной величины логарифмического декремента.

Изменять индуктивность (или емкость) целесообразно два раза за период, следовательно частота изменения параметра (частота параметрического резонанса) должна быть вдвое выше собственной частоты колебательной системы:

Вот и вырисовался путь возбуждения колебаний в контуре без необходимости изменять непосредственно ЭДС или ток. Начальный флуктуационный ток в контуре так или иначе всегда присутствует, и это даже не принимая во внимание наводки от радиочастотных колебаний в атмосфере.

Если индуктивность (или емкость) будут изменяться не скачками а гармонически, то условие возникновения колебаний станет выглядеть несколько иначе:

Так как емкость и индуктивность — это параметры контура (как масса маятника или упругость пружины), то и способ возбуждения колебаний получил называние параметрического возбуждения.

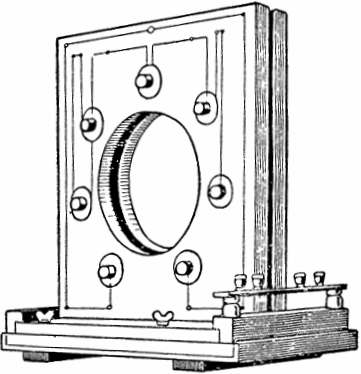
Данное явление открыли и изучали на практике в начале 20 века советские физики Мандельштам и Папалекси. На основе данного физического явления они построили первый параметрический генератор переменного тока мощностью 4 кВт на изменяющейся индуктивности.

В конструкции генератора семь пар плоских катушек располагались по две стороны на каркасе, в полости которого вращался ферромагнитный диск с выступами. Когда диск приводился во вращение мотором, его выступы периодически входили в пространство между каждой парой катушек, и выходили из него, тем самым изменяя индуктивность и возбуждая колебания.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

§ 35. Вынужденные электромагнитные колебания

Какие механические колебания называют вынужденными?

Чему равна частота вынужденных колебаний?

Какое явление называют резонансом?

1. Рассматривая процессы в колебательном контуре, видели, что в нём происходят превращения энергии электрического поля в энергию магнитного поля. Если бы не было потерь энергии, то максимальная энергия электрического поля была бы равна максимальной энергии магнитного поля и сумма энергии магнитного и электрического полей в любой момент времени была бы одинаковой. В реальных процессах, однако, часть энергии расходуется на преодоление сопротивления контура и превращается во внутреннюю энергию. Поэтому суммарная энергия электрического и магнитного полей с течением времени уменьшается и колебания затухают.

Таким образом, свободные электромагнитные колебания являются затухающими.

Чтобы затухание колебаний происходило медленнее, необходимо уменьшить сопротивление контура, при этом уменьшится энергия, идущая на нагревание проводников.

Затухающие колебания вы уже наблюдали на опыте (см. рис. 114). Вы видели, что при замыкании переключателем цепи контура стрелка гальванометра начинала колебаться, однако амплитуда колебаний достаточно быстро уменьшалась; они затухали. График зависимости силы тока затухающих колебаний от времени приведён на рисунке 116.

2. Для того чтобы получить незатухающие колебания, необходимо периодически передавать контуру энергию, которая будет компенсировать потери энергии. Чтобы это осуществить, можно включить в контур источник, напряжение которого изменяется периодически, с определённой частотой. В этом случае в контуре будут существовать вынужденные электромагнитные колебания, происходящие с частотой, равной частоте изменения напряжения источника тока.

Если в контуре существуют вынужденные колебания, то это означает, что заряд конденсатора, сила тока, энергия электрического и магнитного полей периодически изменяются с частотой приложенного переменного напряжения.

3. В том случае, когда частота переменного напряжения совпадает с частотой колебаний контура, наступает резонанс. При этом наблюдается увеличение силы тока. Оно связано с тем, что энергия поступает в контур с той же частотой, с какой расходуется. Резонанс электромагнитных колебаний аналогичен резонансу механических колебаний.

Явление резонанса широко применяется в радиотехнике. Оно используется, например, при настройке радиоприёмника или телевизора на какую-нибудь радиостанцию. Поворачивая ручку настройки, мы изменяем ёмкость конденсатора и, следовательно, частоту электромагнитных колебаний в контуре. Когда эта частота совпадёт с частотой, на которой работает передающая радиостанция, наступит резонанс. Сила тока в контуре радиоприёмника достигнет максимума, а принимаемый сигнал данной частоты будет иметь наибольшую громкость.

Вопросы для самопроверки

1. Почему свободные электромагнитные колебания являются затухающими?

2. Что нужно сделать, чтобы колебания в контуре были незатухающими?

3. С какой частотой происходят вынужденные электромагнитные колебания?

4. Где используется явление резонанса электромагнитных колебаний?

Источник

Получение незатухающих колебаний в контуре

Пополнять энергию колебательного контура можно, подзаряжая конденсатор. Для этого контур подключают к источнику тока. Контур подключается к источнику тока только в те интервалы времени, когда пластина конденсатора, присоединенная к положительному полюсу источника, заряжена положительно.

Если источник постоянного тока будет все время подключен к контуру, то в первую половину периода Т энергия поступает в контур, а следующую половину Т возвращается в источник, т. е. колебания затухают.

Незатухающие колебания установятся в том случае, если контур будет подключаться к источнику только в первую половину периода. Для выполнения такого условия ключ должен замыкать и размыкать цепь с частотой, соответствующей частоте электромагнитных колебаний контура (формула 7). Однако механический ключ инертен. Безынерционным ключом является транзистор. Транзистор обеспечивает поступление энергии к колебательному контуру, если напряжение на электронном переходе меняется синфазно (в одной фазе) с напряжением на контуре.

Источник

СВОБОДНЫЕ НЕЗАТУХАЮЩИЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ.

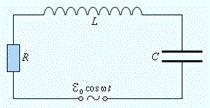
Свободные незатухающие электромагнитные колебания можно получить в электрической цепи, состоящей из последовательно соединенных конденсатора емкостью С, катушки индуктивностью L и резистора сопротивлением R:

Такую электрическую цепь называют колебательным контуром, потому что в ней могут происходить периодические изменения электрического заряда и разности потенциалов на обкладках конденсатора, а также электрического тока в цепи. Периодические колебания перечисленных физических величин достаточно вызвать даже при кратковременном подключении конденсатора колебательного контура к источнику постоянного тока. Однако, из-за потерь электрической энергии, связанной с нагреванием катушки и резистора, имеющих электрическое сопротивление R, колебания в контуре будут затухающими.

Свободные незатухающие электромагнитные колебания можно получить только в идеализированном случае, когда можно пренебречь электрическим сопротивлением (R 0) контура. Такие свободные незатухающие колебания называют еще собственными электромагнитными колебаниями.

Можно доказать, что в колебательном контуре происходят гармонические колебания заряда, согласно закону:

, (1)

, (2)

Форма записи (через cos или sin) не имеет значения, так как отличие будет определяться лишь начальными условиями, а именно различной начальной фазой колебаний. Зная связь между зарядом конденсатора и разностью потенциалов на его обкладках:

, (3)

можно аналогично записать гармонические колебания разности потенциалов:

, (4)

, (5)

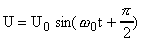
Сила тока является первой производной от электрического заряда по времени:

. (6)

Поэтому гармонические колебания силы тока в колебательном контуре будут происходить по закону:

, (7)

. (8)

Период собственных электромагнитных колебаний, соответственно, вычисляется по формуле (Формула Томсона.):

. (9)

Физические процессы, происходящие в колебательном контуре, сопровождается непрерывными преобразованиями одного вида энергии в другой, а именно: энергия электрического заряда конденсатора превращается в энергию магнитного поля катушки и наоборот. При этом, в полном соответствии с законом сохранения и превращения энергии, полная энергия в колебательном контуре остается величиной постоянной:

, (10)

ПЕРИОД И ЧАСТОТА КОЛЕБАНИЙ.

Более крупные единицы частоты-килогерц (пишут: кГц), равный 1000 Гц, и мегагерц (пишут: МГц), равный 1000 кГц, или 1000000 Гц.

Вынужденные электромагнитные колебания. Установившиеся вынужденные электромагнитные колебания. Дифференциальное уравнение вынужденных колебаний и его решение методом векторных диаграмм. Явление резонанса. Резонанс токов и напряжений.

Вынужденные колебания.

Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями.

Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.

Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω₀.

Если частота ω₀ свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте ω внешнего источника.

Для установления стационарных вынужденных колебаний необходимо некоторое время Δt после включения в цепь внешнего источника. Это время по порядку величины равно времени τ затухания свободных колебаний в цепи.

Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического источника тока, называются цепями переменного тока.

Рассмотрим последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рис. 2.3.1):

где ₀ – амплитуда, ω – круговая частота.

Вынужденные колебания в контуре

Предполагается, что для электрической цепи, изображенной на рис. 2.3.1, выполнено условие квазистационарности. Поэтому закон Ома можно записать для мгновенных значений токов и напряжений:

Величина – это перенесенная с изменением знака из правой части уравнения в левую ЭДС самоиндукции катушки. Эту величину принято называть напряжением на катушке индуктивности.

Уравнение вынужденных колебаний можно записать в виде

где u_R(t), u_C(t) и u_L(t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами U_R, U_C и U_L. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока. Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм.

На векторной диаграмме колебания определенной заданной частоты ω изображаются с помощью векторов (рис. 2.3.2).

Рисунок 2.3.2.

Изображение гармонических колебаний A cos (ωt + φ₁), B cos (ωt + φ₂) и их суммы C cos (ωt + φ) с помощью векторов на векторной диаграмме Длины векторов на диаграмме равны амплитудам колебаний A и B, а наклон к горизонтальной оси определяется фазами колебаний φ₁ и φ₂. Взаимная ориентация векторов определяется относительным фазовым сдвигом Δφ = φ₁ – φ₂. Вектор, изображающий суммарное колебание, строится на векторной диаграмме по правилу сложения векторов:

Для того, чтобы построить векторную диаграмму напряжений и токов при вынужденных колебаниях в электрической цепи, нужно знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для всех участков цепи.

Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R, конденсатору емкости C и катушки индуктивности L. Во всех трех случаях напряжения на резисторе, конденсаторе и катушке равны напряжению источника переменного тока.

Резонанс

Явление возрастания амплитуды колебаний тока при совпадении частоты ω внешнего источника с собственной частотой ω₀ электрической цепи называется электрическим резонансом. При резонансе

Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).

При последовательном резонансе (ω = ω₀) амплитуды U_C и U_L напряжений на конденсаторе и катушке резко возрастают:

Было введено понятие добротности RLC-контура:

Таким образом, при резонансе амплитуды напряжений на конденсаторе и катушке в Q раз превышают амплитуду напряжения внешнего источника.

Резонансные кривые для контуров с различными значениями добротности Q. Рис. 2.3.4 иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды U_C напряжения на конденсаторе к амплитуде ₀ напряжения источника от его частоты ω для различных значений добротности Q. Кривые на рис. 2.3.3 называются резонансными кривыми.

Источник