что необходимо знать чтобы измерить объем мяча ответ
Что необходимо знать чтобы измерить объем мяча ответ
Смотря, сколько вам нужно уместить) Если вам будет мало, я продам вам еще один автобус для теннисных мячиков )
Но так как вопрос действительно интересный, да и первый комментатор поразил высотой автобуса в 2м (надеюсь, он про высоту потолка), мне стало интересно посчитать), да и диаметр теннисного мяча не 10 см, а в среднем 6,7, я реши посчитать, хоть этого и не требует задача)
Самое интересное в этой задаче, что даже сам автор поста не будет знать точного ответа ) На самом деле, если все считать математически, то разница в 1 см в высоте потолка может дать нам очень большую разницу в количестве мячей, поместившихся в автобусе. Вопрос в соотношении мячей к объему коробки. чем больше мячей, тем точнее число. так представив себе коробку размерами 20х20х20 см и шарики диаметром 10 см, получим, что в такую коробку поместится 8 шаров. Увеличив каждую сторону коробки всего лишь на
1,5 см, можно поместить туда 9-й шар. Да, именно в самый центр. и так далее. Путем нехитрых расчетов, получаем соотношение 68% от объема. Взяв, к примеру, ПАЗ и вычеслив его внутренний объем, исключая сиденья, педальный узел, руль, и пр., получаем 18.377 мячей)
Исследовательская работа » Вычисление объёмов»
Оглавление
Введение
В пятом классе на уроках математики мы познакомились с понятием объёма тела и научились вычислять объём прямоугольного параллелепипеда. Объём прямоугольного параллелепипеда вычисляется очень просто: нужно измерить его ширину, длину, высоту и перемножить их.
А как измерить или вычислить объём тела другой формы?
Всегда ли можно измерить объем любого тела?
Как давно появились формулы для нахождения объёма и кто первым открыл их?
Зачем человеку нужно уметь измерять и вычислять объемы тел на практике?
В каких единицах можно рассчитать объем?
Где мы можем применить свои знания об объёмах?
На все эти вопросы мы решили ответить.
Цель работы:
— узнать формулы для вычисления различных геометрических тел, научиться ими пользоваться при вычислении объёмов;
— узнать исторические сведения об объёмах тел;
— найти методы измерения и вычисления объемов нестандартных тел в повседневной жизни.
Теоретическая часть
Так что же такое объём?
Во первых мы нашли в энциклопедии определение объёма тел.
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п.
В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от латинского volume — «объём», «наполнение».
За единицу измерения объема принимается куб, ребро которого равно единице измерения отрезков.
Объёмы обладают следующими свойствами:
1. Объем тела есть неотрицательное число;
2. Равные тела имеют равные объемы;
3. Если тело составлено из нескольких тел, то его объем равен сумме объемов этих тел.
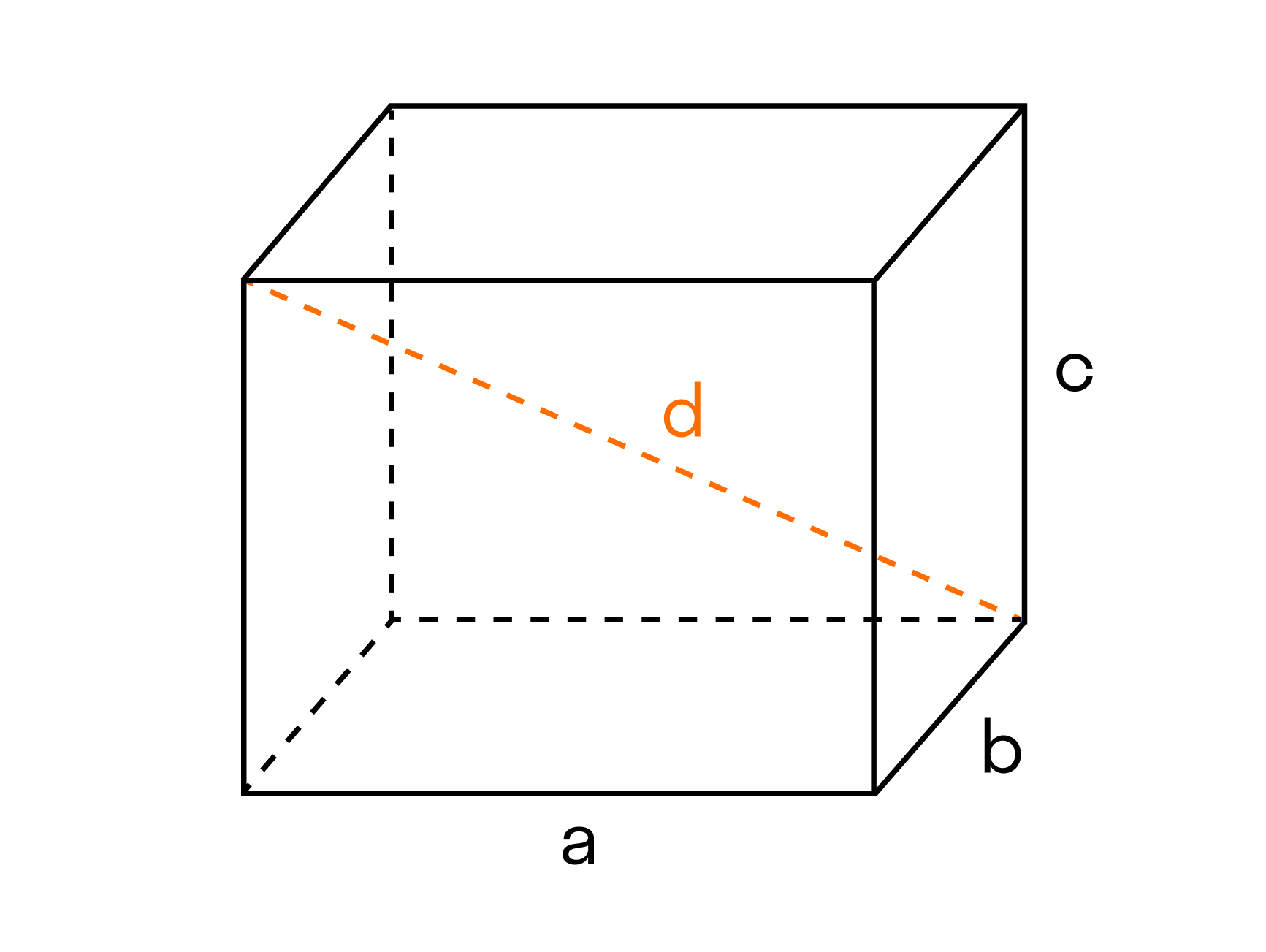
Согласно третьему свойству, чтобы найти объём прямоугольного параллелепипеда, нужно разбить его на кубы с ребром, равным единице измерения. Но такой способ измерения объёмов неудобен, поэтому применяют формулу для вычисления объёма прямоугольного параллелепипеда
V=a·b·c
Формулы для вычисления других геометрических тел немного сложнее.
Мы нашли их в учебнике геометрии 11класса и с их помощью вычислили объёмы мяча, конуса, шестигранной пирамиды и шестигранной призмы.
Формула для вычисления объёма шара V = , где R- радиус шара, π ≈ 3,14
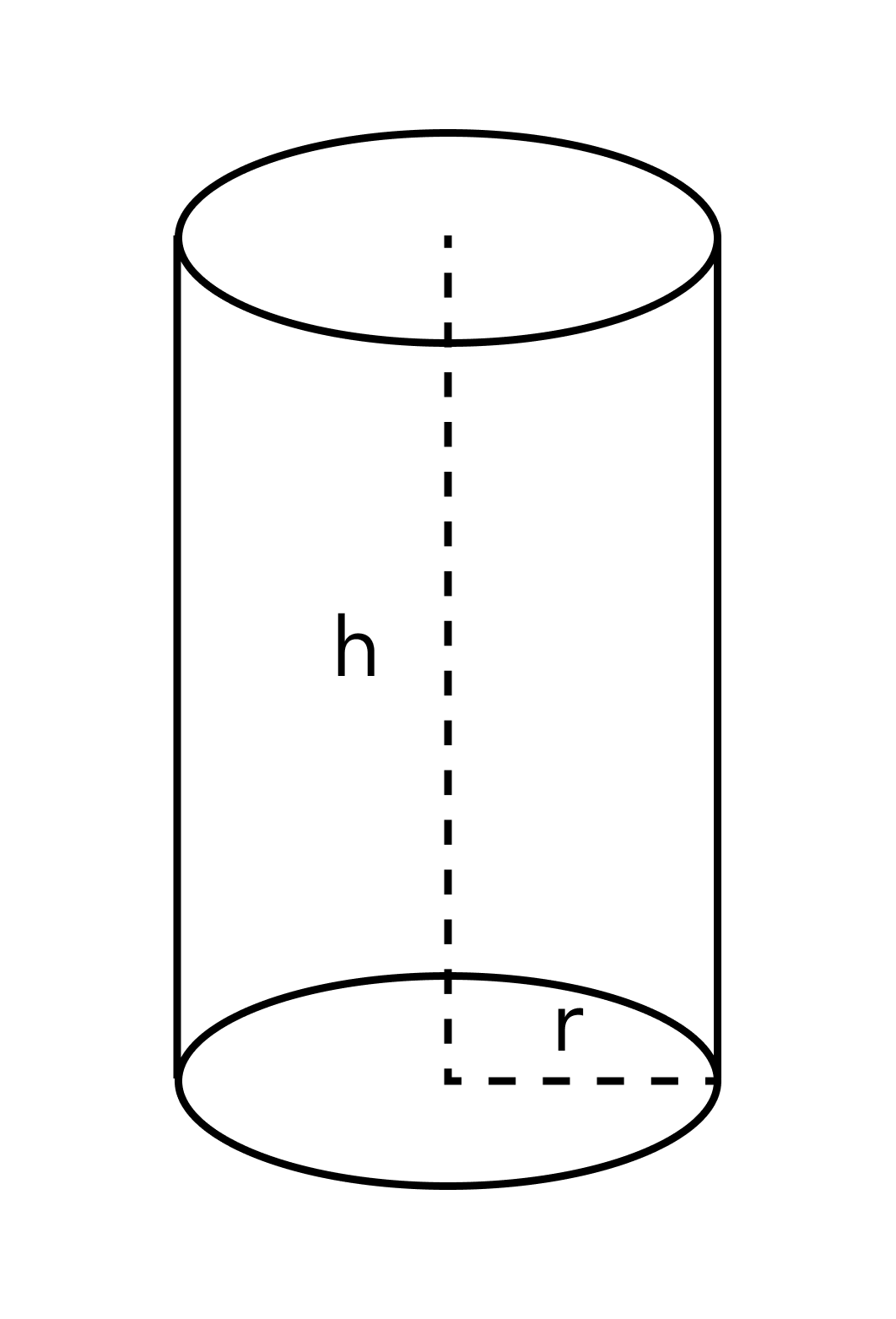
h – высота цилиндра
где R- радиус шара, h – высота конуса, π ≈ 3,14
Формула для вычисления объёма усечённого конуса
V = = + R
Формулы для вычисления объёма пирамиды и усечённой пирамиды
V=
Sниж — площадь нижнего основания, ABCDE
Sверх — площадь верхнего основания, abcde
История вычисления объёмов
Практическое применение геометрии начинается с древних времён. Египтяне использовали эту науку в различных хозяйственных работах, при сооружении оросительных каналов, грандиозных храмов и пирамид, при высечении из гранита знаменитых сфинксов и т.п.
Содержащиеся в дошедших до нас папирусах геометрические сведения и задачи почти все относятся к вычислению площадей и объемов. В них нет никаких указаний на способы вывода тех правил, которыми пользовались египтяне для вычисления длин, площадей и объёмов; часто употреблялись правила приближённых подсчётов. Высшим достижением египетской геометрии следует считать точное вычисление объёма усечённой пирамиды с квадратным основанием, содержащееся в «Московском папирусе».
Практическое применение формул для вычисления объёмов
Мы решили применить свои знания на практике.
По санитарным нормам объём воздуха, приходящийся на одного ученика должен составлять 4-5. Мы решили проверить, выдерживаются ли эти нормы в кабинете математики. Измерили длину, ширину и высоту класса. Получили следующие результаты a = 7,7м, b = 6,15м, с = 3,15м.
V = 7,7. В нашем классе учится 26 человек. Вместе с учителем нас 27 человек.
2. Вычислили объёма мяча.
Измерили с помощью рулетки длину окружности мяча С = 44, 5 см
С помощью формулы С = π d вычислили d d = 44,5:3,14≈14,1 см
Нашли радиус мяча R = d : 2 R=7,05см
Вычислили объём V = • 3,14• 1467 V= 1,467
3. Вычислили объём модели шестигранной пирамиды
Вычислили площадь основания пирамиды. В основании лежит правильный шестиугольник. Чтобы найти площадь, мы разбили его на 6 равных треугольников.
Площадь треугольника можно вычислить по формуле S = a h, где а- основание треугольника, h – его высота.
а= 5,2см, h = 4,5см Sосн= 6 = 70,2
= 20см
V = = 468
4. Вычислили объём модели конуса.
Измерили радиус конуса и его высоту: R=5cм,h=14,5 см
V = = 379
5. Вычислили объём модели шестигранной призмы
Измерили высоту призмы, сторону основания призмы, разбили основание на треугольники, измерили высоту треугольника: Hпризмы = 16,5см, а=4,8см, h=4,2см
V = = 998
Мы поняли, что если тело имеет правильную геометрическую форму, то вычислить его объём не очень сложно. Для этого нужно знать формулы и значения букв, входящих в эти формулы.
А как быть, если тело не имеет правильной формы? Как вычислить объём мраморной черепашки? Мы пошли по пути великого Архимеда.
Легенда об Архимеде
«Царь Гиерон и Архимед были очень хорошими друзьями. И однажды в мысли царя закралась тень сомнения по поводуювелира, который сделал для него новую корону. Он не был уверен, что корона была из чистого золота, которое он лично отдал ювелиру на её создание. Царь поделился своими подозрениями с Архимедом, и попросил выяснить, все ли золото было использовано на создание короны. Архимеду оказалось по душе предложенная задачка, и он тут же принялся искать для нее решение. Но Архимед переоценил свои силы и никак не мог найти решение. Он почти отчаялся уже найти ответ, и решил принять ванну. Его голова все так же была занята мыслями о короне, и как только Архимед погрузился в ванну, из нее выплеснулась часть воды. Он немного подумал и понял, что вода, выплеснувшаяся из ванны равна объему его собственного тела и таким же способом можно было найти объем короны, который так необходим был для решения этой задачи. «Эврика!» – закричал Архимед.
Он тут же бросился бежать к царю Гиерону, так сказать в «чем мать родила», ведь наука не требует отлагательств. И рассказал, как можно разоблачить или доказать честность ювелира. Он приказал принести необходимые приборы и тут же провел опыт, благодаря которому узнал объем короны. Так же он узнал объем слитка, аналогичному, который получил от царя ювелир.
Таким образом он доказал виновность ювелира и открыл знаменитый« закон Архимеда».
Мы решили проверить, действительно ли объём тела равен объёму вытесняемой им жидкости.
Для этого мы вычислили объёмы двух металлических цилиндров с помощью формул, а затем нашли объём этих же цилиндров методом полного погружения их в воду.
Получили следующие результаты:
R = 1,25см Н = 4см V = • • H =3,14 4 19,6
При погружении цилиндра в воду, объём вылившейся воды оказался равным 20 мл
1мл = 0,001 = 1 , значит объём первого цилиндра V = 20
R = 2,1см Н = 10 см V = • • H =3,14 10 138,5
При погружении цилиндра в воду, объём вылившейся воды оказался равным
138 мл
Опыты и измерения показали, что с помощью погружения тела в воду, можно с большой точностью измерить его объём.
Таким способом мы измерили объём гайки и объём черепашки
Практическое применение формул для вычисления объёмов.
Чтобы применить ту или иную формулу для вычисления объёма тела, нужно, чтобы оно имело геометрическую форму: цилиндр, шар, конус и т.д. Но часто встречаются предметы, которые не обладают идеальной с точки зрения геометрии формой (бочки, деревья и т.д). Нет ли такой универсальной формулы, по которой можно вычислить объем любого тела? Оказалось, что такая формула существует; она пригодна для любого тела (конуса, пирамиды, шара и т.д.) Эта замечательная формула известна в математике под названием формулы Симпсона. Томас Симпсон (1710-1761)- английский математик. В 1743 вывел формулу приближённого интегрирования (формула Симпсона). Другие работы Симпсона посвящены элементарной геометрии, тригонометрии, анализу и теории вероятностей
Вот как выглядит эта формула: V=h/6(a+4b+c), где
С помощью данной формулы можно найти объём ствола срубленного дерева. Этот метод вычисления объема применяется в лесной промышленности
Если сравнить объемы цилиндра, шара и куба с одинаковой площадью поверхности, то получится, что объем цилиндра больше, чем объем куба, но меньше, чем объем шара. То есть с экономической точки зрения выгоднее изготавливать ёмкости цилиндрической или шарообразной формы для хранения и перевозки веществ
( цистерны для нефти, консервные банки). Изготавливают ёмкости цилиндрической формы, т.к шарообразные неудобны в использовании.
Вывод
Велика роль геометрии в нашем современном мире. В своей практической деятельности человек часто встречается с необходимостью вычисления объёмов, например, при изготовлении каких-либо деталей или при строительстве различных сооружений. Многие строительные объекты, детали конструкций и другие предметы имеют форму геометрических тел: параллелепипедов, призм, цилиндров, шаров и т.д. Поэтому формулы для вычисления объёмов нужно знать и уметь применять при решении математических задач и в жизни.
Плотность вещества
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Масса
Начнем с самого сложного — с массы. Казалось бы, это понятие мы слышим с самого детства, примерно знаем, сколько в нас килограмм, и ничего сложного здесь быть не может. На самом деле, все сложнее.
В Международном бюро мер и весов в Париже есть цилиндр массой один килограмм. Материал этого цилиндра — сплав иридия и платины. Его масса равна одному килограмму, и этот цилиндр — эталон для всего мира.
Высота этого цилиндра приблизительно равна 4 см, но чтобы его поднять, нужно приложить немалую силу. Необходимость эту силу прикладывать обуславливается инерцией тел и математически записывается через второй закон Ньютона.
Второй закон Ньютона
F = ma
В этом законе массу можно считать неким коэффициентом, который связывает ускорение и силу. Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.
Закон Всемирного тяготения
F = GMm/R2
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
G = 6.67 × 10-11 м3 кг-1 с-2
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз. Когда думаешь об этом, хочется взвешиваться исключительно на Луне🙃
Откуда берется масса
Физики убеждены, что у элементарных частиц должна быть масса. Доказано, что у электрона, например, масса есть. В противном случае они не могли бы образовать атомы и всю видимую материю.
Вселенная без массы представляла бы собой хаос из различных излучений, двигающихся со скоростью света. Не существовало бы ни галактик, ни звезд, ни планет. Здорово, что это не так, и у элементарных частиц есть масса. Только вот пока непонятно, откуда эта масса у них берется.
Мужчину на этой фотографии зовут Питер Хиггс. Ему мы обязаны за предположение, экспериментально доказанное в 2012 году, что массу всех частиц создает некий бозон.
Бозон Хиггса невозможно представить. Это точно не частица в форме шарика, как обычно рисуют электрон в учебнике. Представьте, что вы бежите по песку. Бежать ощутимо сложно, как будто бы увеличилась масса. Частицы пробираются в поле Хиггса и получают таким образом массу.
Объем тела
Объем — это физическая величина, которая показывает, сколько пространства занимает тело. Это важный навык — уметь объемы соотносить. Например, чтобы посчитать, сколько пластиковых шариков помещается в гигантский бассейн.
Например, чтобы рассчитать объем прямоугольного параллелепипеда, нам нужно перемножить три его параметра.
Формула объема параллелепипеда
V = a*b*c
А для цилиндра будет справедлива такая формула: