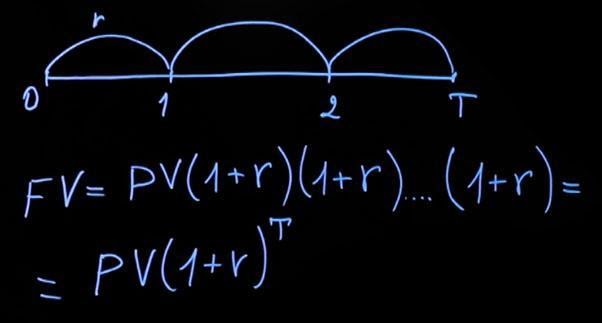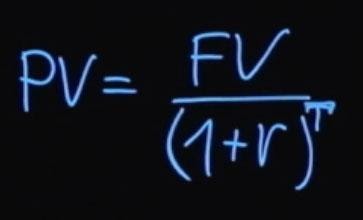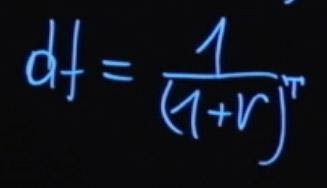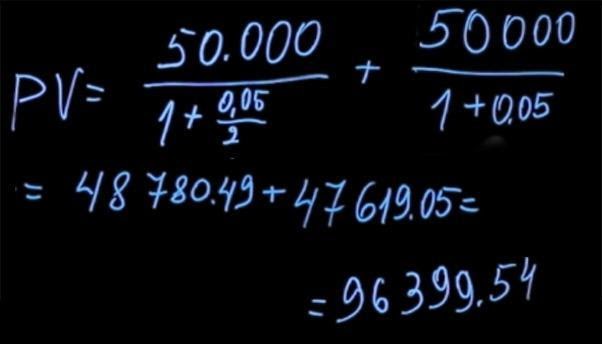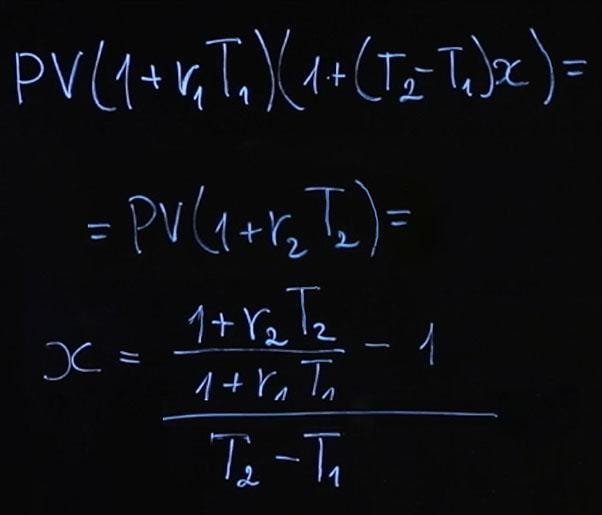что брать за ставку дисконтирования

Дисконтирование. Какую ставку применить

Одним из основных элементов метода бухгалтерского учёта является оценка.

В Концептуальных основах представления финансовых отчётов, принятых Советом по МСФО (см. сайт Минфина РФ), оценке посвящена отдельная глава.

Учётная оценка – это процесс определения (расчёта) сумм, в которых факты хозяйственной жизни отражаются в учёте и отчётности.

Оценить объект бухгалтерского учёта – значит выбрать конкретный метод оценки из предлагаемых стандартами: первоначальная (историческая) стоимость (себестоимость); текущая (восстановительная) стоимость (с учётом переоценки); цена продажи (погашения) (справедливая стоимость); приведённая (текущая дисконтированная) стоимость.

В соответствии с МСФО (IFRS) 13 «Оценка справедливой стоимости», приведённая стоимость – это эквивалент будущего денежного потока, рассчитанный на дату оценки с учётом процентной ставки.

Временная стоимость денег – это экономическая концепция, по которой определённая сумма денег в настоящий момент представляет большую ценность, чем в будущем. Большую ценность денежным средствам сейчас придают такие факторы, как:

— способность денежных средств приносить доход;

— риск невозврата денежных средств (или их части) в будущем;

О необходимости рассчитывать приведённую стоимость говорится во многих стандартах бухгалтерского учёта: ПБУ 8/2010 «Оценочные обязательства, условные обязательства и условные активы» (п. 20), ФСБУ 5/2019 «Запасы» (п. 13), ФСБУ 6/2020 «Основные средства» (п.23), ФСБУ 26/2020 «Капитальные вложения» (п. 10, 12), ФСБУ 25/2018 «Бухгалтерский учёт аренды» (п. 14,15,25,26). Необходимость таких расчётов связана с приобретением ценностей с отсрочкой платежей (если она составляет более 12 месяцев), с включением в их стоимость оценочных обязательств (например, в стоимость капитальных вложений нужно включить оценочное обязательство по будущему демонтажу, утилизации основных средств и восстановлению окружающей среды), с определением обязательства по аренде.

Формула расчёта приведённой суммы в общем виде выглядит следующим образом

где PV (presentvalue) — приведенная (дисконтированная) стоимость;

n — номер периода (обычно годового);

CFn (cashflow) — денежный поток на конец n-го периода;

i — процентная ставка

Процентная ставка в этой формуле – важнейшая составляющая. Выбор ставки – предмет профессионального суждения.

В Рекомендации БМЦ¹ Р-65/2015-КпР «Ставка дисконтирования» предлагается следующий вариант выбора.

Если первоначальная дисконтированная стоимость актива или обязательства может быть определена прямым путём, организация применяет фактическую ставку дисконтирования.

Покупаем актив с отсрочкой платежа за 1 200 тыс. руб. Без отсрочки он стоил бы 1 000 тыс. руб., согласно маркетинговой политике поставщика. Следовательно, дисконтированная стоимость актива – 1 000 тыс. руб.

Если нет возможности определить прямую ставку дисконтирования – ориентируемся на ставку доходности по долговым инструментам с наиболее близкими параметрами.

В МСФО (IFRS) 13 «Оценка справедливой стоимости» уточняется, что ставка дисконтирования, используемая при определении справедливой стоимости активов или обязательств, а также при оценке возмещаемой суммы активов:

— должна основываться на данных рынка;

— должна принимать во внимание риски, связанные с прогнозируемыми денежными потоками по активу или обязательству;

— должна учитывать риски, характерные для организации (риск отрасли, риск продукта и т. д.), рыночные риски, включая страновой риск, валютный риск и ценовой риски (п. А18 МСФО (IAS) 36 «Обесценение активов» и п. 22 МСФО (IFRS) 13 «Оценка справедливой стоимости»).

То же относится к расчёту оценочных обязательств.

В ПБУ 8/2010 «Оценочные обязательства, условные обязательства и условные активы» также говорится, что выбранная организацией ставка дисконтирования должна учитывать существующие на финансовом рынке условия, а также специфичные риски обязательства.

Согласно стандартам ФСБУ 25/2018 «Бухгалтерский учёт аренды» и МСФО (IFRS) 16 «Аренда», при формировании стоимости инвестиции в аренду и обязательства по аренде, ставку дисконтирования принимают равной ту, что указана в договоре аренды (если она легко определяется), либо ту, по которой арендатор привлекает или мог бы привлечь заёмные средства на срок, сопоставимый со сроком аренды (п.14, 15, 33 ФСБУ 25/2018).

Сложность определения ставки дисконтирования в данном случае может быть в том, что её применение должно давать возможность определить справедливую стоимость предмета аренды (п.15 ФСБУ 25/2018).

Выбор периода дисконтирования, ставки дисконтирования и определение самих денежных потоков являются примером применения профессионального суждения.

Пример расчёта дисконтированной стоимости

Стоимость внеоборотного актива 300 000 руб., ставка дисконтирования – 10 %, отсрочка в оплате – 3 года. Дисконтированная стоимость будет равна: 225 394 руб. (300 000 : (1 + 0,1) ^3), в учете отразим Дт 08 Кт 60 – 225 394. Далее ежегодно будем отражать прирост кредиторской задолженности перед поставщиком.

Через год дисконтированная стоимость будет равна 225 394 х 110% = 247 933, прирост составит 22 539 руб. (247 933 – 225 394 = 22 539), в учёте сделаем запись Дт 91/2 Кт 60 – 22 539 руб. К концу третьего года кредиторская задолженность на счете 60 составит 300 000 руб.

Источник

Для инвесторов: что такое ставка дисконтирования

Давайте сегодня разберемся в том, что такое ставка дисконтирования. Это важное понятие, которое пригодится любому инвестору. Из этой статьи вы узнаете, зачем нужна ставка дисконтирования, где она используется и какие есть методы ее расчета.

Что такое ставка дисконтирования

Если говорить простыми словами, ставка дисконтирования — это расчетная величина, которая позволяет оценить доходность будущих инвестиций. Она помогает привести будущие денежные потоки к единому знаменателю и, за счет этого, выбрать из нескольких вариантов инвестиций самый выгодный.

Если оперировать математическими категориями, то дисконтирование — это процесс, обратный начислению сложных процентов. Легче всего разобраться на примере:

Предложение банка — вклад на два года под 10% с капитализацией процентов. Допустим, вы хотите узнать, сколько денег нужно положить в банк, чтобы через два года забрать 200 тысяч рублей:

200 000 рублей = Х × (1 + 0,1)²,
где 0,1 — ставка банка (10%);
Х = 165 289, 25 рублей.

Получается, сегодня вам нужно вложить 165 289, 25 рублей, чтобы через 2 года получить 200 тысяч рублей.

У ставки дисконтирования можно выделить несколько значений:

Где используется ставка дисконтирования

Ставку дисконтирования используют для оценки и сравнения различных инвестиционных проектов.

Также ставка дисконтирования нужна, чтобы привести будущие денежные потоки к сегодняшнему дню. Например, понять, какова будет чистая доходность инструмента/бизнеса с учетом других условий (взятого кредита, инфляции и т.д.).

Кроме того, в ставке дисконтирования можно учесть минимальный уровень безрисковой доходности, инфляцию и риски конкретных вложений.

В экономике существует много вариантов расчета ставки дисконтирования, но нет единого мнения, как ее вычислить наиболее эффективно и просто. Давайте рассмотрим основные методы расчета ставки.

Методы расчета ставки

Методов очень много, поэтому разумнее выделить группы методов и разобраться с ними:

Теперь давайте разберемся с некоторыми методами поподробнее:

«Интуитивный» метод

В этом случае инвестор сам определяет ставку дисконтирования, исходя из своих ожиданий и желаний. Это субъективный метод. Здесь нет места сложным математическим формулам. К примеру, инвестор может просто сложить безрисковую доходность и инфляцию для определения ставки.

Метод на основе экспертной оценки

Этот метод основан на оценках экспертов-инвесторов, в нем тоже не используют математические расчеты. Определение ставки происходит на комиссиях экспертов, где они обсуждают и голосуют за варианты ставок.

Чтобы получилось числовое выражение, оценки нескольких экспертов усредняются. Этот метод тоже считается субъективным.

Аналитические методы

Эта группа расчетов при определении ставки дисконтирования учитывает финансовые мультипликаторы и показатели компаний. Рассмотрим два вида аналитического расчета.

1. Расчет на базе показателей рентабельности

В этой модели ставку дисконтирования определяют на основе показателей рентабельности капитала. Например, по рентабельности собственного капитала ROE или по рентабельности активов ROA. Данные для расчета берут из бухгалтерского баланса и отчета о прибылях и убытках.

Данный метод не учитывает прогнозное изменение финансовых показателей, то есть может давать ошибку для долгосрочных проектов.

2. Расчет на основе модели Гордона

Эта модель оценивает собственный капитал компании, состоящий из акций. В основе лежит предположение, что стоимость акции равна стоимости всех будущих дивидендов. Эту модель можно применить только для предприятий, которые регулярно выплачивают дивиденды. Формула расчета ставки дисконтирования по модели Гордона:

где DIV — это величина ожидаемых дивидендов на одну акцию за год;
g — темпы прироста дивидендов. Модель предполагает, что дивиденды стабильно растут на определенный процент. Это может вызывать трудности при расчетах, потому что на российском рынке стабильно растущих компаний мало. Усредненные темпы роста могут искажать результаты;
P — цена размещения акций;
fc — затраты на эмиссию в процентах.

Модель расчета на основе рыночных мультипликаторов

За ставку дисконта в этом методе берут средневзвешенное значение доходности, которое рассчитывается по опережающим рыночным мультипликаторам. В этом случае рассматривают следующие коэффициенты:

Расчет ставки дисконтирования на основе премий за риск

Методы этой группы при расчете ставки дисконтирования учитывают безрисковую ставку, инфляцию и премию за риск. Безрисковую ставку и инфляцию считают примерно одинаково, а вот премии за риск выбирают разные.

Методы оценки премии за риск. Специфические риски встречаются в любом проекте. Единой методики оценки специфических рисков не существует. Как правило, аналитики самостоятельно выбирают наиболее значимые факторы для конкретного проекта. После они оценивают эти факторы в процентах и складывают. Вот некоторые методики оценки премии за риск:

Метод на основе модели WACC

WACC — это средневзвешенная стоимость совокупного капитала фирмы. Совокупный капитал состоит из собственного и заемного капитала. Основная идея в том, что затраты на капитал должны быть меньше, чем денежные потоки, которые он приносит. Экономический смысл этой модели заключается в вычислении минимально допустимого уровня доходности бизнеса.

Расчет ставки дисконтирования можно разделить на 4 этапа:

WACC рассчитывается по формуле:

где T — ставка налога на прибыль, на которую становится меньше требуемая доходность заемного капитала;
w_d — доля заемного капитала;
r_d — ставка по заемному капиталу;
w_e — доля собственного капитала;
r_e — ставка по собственному капиталу.

Применять модель WACC может быть сложно из-за того, что стоимость собственного капитала зачастую оценить невозможно. Кроме этого, в модели не учитывается риск различных инвестиций. Цена заемного капитала может быть рассчитана неверно из-за льготных схем кредитования.

Ставка дисконтирования в России

В рыночной экономике все методы дали бы сопоставимые результаты. Но в российской экономике это не работает.

Ставка дисконтирования на Западе существенно ниже, чем в России, потому что на Западе — низкая инфляция и устойчивый курс внутренней валюты. Кроме этого, ставки рефинансирования на Западе приближаются к 0, а в некоторых странах — даже ниже 0.

В российских промышленных инвестиционных проектах ставка дисконтирования определяется от 10 до 40%, потому что экономика нестабильна, а потребительские цены растут больше, чем на 8—10%. Ставку дисконтирования, как правило, считают складывая ключевую ставку ЦБ + риски. Риски в России могут доходить до 20%.

Источник

Стоимость денег, типы процентов, дисконтирование и форвардные ставки. Ликбез для гика, ч.1

Представьте себе ситуацию – вы покупаете машину, и вам предлагают два варианта: заплатить с рассрочкой в несколько месяцев или погасить всю сумму сразу и с небольшой скидкой. Какой окажется выгоднее?

Или, например, вы хотите разместить вклад на год. Можно положить на весь срок под высокий процент или на отдельные короткие сроки под более низкий. Что лучше и насколько?

Все ответы под катом. И добро пожаловать в мир, где время — всегда деньги. До этого вы знали об этом, но теперь — в деталях и с примерами.

Меня зовут Мария Абрашкина, я математик и Product Owner в команде по расчету портфельных рисков. А также один из авторов видеокурса про финансовую математику (Ч.1 – Типы начисления процентов, Ч.2 – Дисконтирование, Ч.3 – Форвардные процентные ставки). В этом посте я расскажу о стоимости денег, процентных ставках и облигациях. Эти знания помогут вам в будущем принимать финансовые решения основываясь на точном расчете, используя простую математику.

#1. Временная стоимость денег. Типы начисления процентов

Сначала поговорим о том, что такое временная стоимость денег, или Time Value of Money (TVM), почему деньги имеют стоимость и какие виды процентов существуют.

На картинке ниже показан список фильмов с максимальными кассовыми сборами.

Можем ли мы их сравнить по этим цифрам? Учитывая, что фильмы выходили в разные годы, вряд ли такое сравнение будет правильным. Как быть?

Давайте рассмотрим более простой пример. Допустим, у вас есть тысяча рублей, и я у вас прошу эту сумму в долг. Сколько вы хотите, чтобы я вам отдала через год? Возможно, вы подумаете, что на эту тысячу рублей вы сейчас можете купить бутылку вкусного вина или что-то другое. Также вы можете предположить, что через год на ту же самую тысячу рублей вы вряд ли сможете купить этот товар по причине инфляции. Кроме того, существует риск, что деньги я не верну. Поэтому, скорее всего, вы захотите компенсацию за то, что вы пока не будете покупать бутылку вина или какую-нибудь другую вещь. Также вам необходим стимул, оправдывающий риск того, что деньги я вам могу и не вернуть. Вероятно, вы потребуете от меня вернуть деньги с какой-то надбавкой, то есть с процентом.

Итак, деньги имеют стоимость, потому что их владелец хочет компенсации за то, что он не может купить какой-то товар или услугу, и за риск, который он несет, давая деньги в долг.

На языке математики это будет выглядеть так:

Если записать эту формулу в общем виде, то будущее значение равняется сумме долга, умноженной на единицу плюс процентная ставка.

А что, если начисление процентов происходит не раз в год, а чаще? Или что если проценты начисляются в течение двух, трех, десяти лет? В данном случае нам нужно всегда уточнять, каким образом происходит начисление процентов, в конце срока или с какой-то периодичностью и на сколько лет.

Простые проценты

Рассмотрим пример, когда проценты начисляются в конце срока вклада. Будущее значение будет равняться текущему значению плюс текущее значение, умноженное на годовую процентную ставку. Годовая процентная ставка будет прибавляться к сумме нашего вклада столько раз, на сколько лет мы сделали вклад.

Если же процентная ставка начисляется каждый год, то формула будет выглядеть иначе.

Рассмотрим ситуацию с начислением за период в несколько лет. Считаем, что действующая процентная ставка на протяжении всего периода будет одинаковая. Тогда формула принимает следующий вид: текущее значение, умноженное на сумму единица плюс процентная ставка, затем еще раз на сумму единицы и процентной ставки и т. д. Умножать следует столько раз, на какое количество лет был сделан вклад. В общем виде формула будет выглядеть следующим образом:

Обратите внимание – если в первом случае к нашему вкладу каждый год прибавлялась сумма процентов (как в первом примере, где добавлялось к сумме вклада 50 рублей), то в случае с ежегодным начислением на 50 рублей, добавленные в первом периоде, у нас каждый раз начисляется процент.

Всегда важно обращать внимание на то, каким образом происходит начисление процентов. Проценты могут начисляться не только раз в год, но и раз в полгода, каждый день. И в принципе нам ничего не мешает начислять эти проценты непрерывно.

Непрерывное начисление процентов

Как же будет выглядеть формула, если мы хотим начислять проценты непрерывно? Тут придется вспомнить школьную математику. Формула будет следующей:

Для того, чтобы привести наш предел к какому-то удобному виду, нам нужно сделать подстановку. В итоге мы получаем следующее:

С учетом того, что наш предел равен числу Эйлера (е=2,71), наша формула преобразуется в очень простое выражение. Текущее значение нашего вклада умножается на экспоненту, которая возводится в степень, представленную произведением процентной ставки и количества лет, на которые начисляются наши проценты.

Давайте сравним, как выглядят платежи в зависимости от периодичности начислений. В таблице представлено будущее значение вклада в сто тысяч рублей, который положен на десять лет по ставке двадцать процентов.

Таким образом сумма вклада при начислении процентов ежегодно в два раза превышает сумму вклада при выплате процентов единожды в конце срока.

Если же начисления производятся непрерывно, то сумма вклада оказывается более 700 тысяч рублей против 300 тысяч рублей при простом начислении процентов.

На графике ниже наглядно показано, как растет итоговая сумма вкладов при разных способах начисления процентов.

Отсюда необходимо сделать вывод:

выбирая вклад, важно смотреть не только на размер процентной ставки, но и на периодичность начисления процентов. Высокая процентная ставка не всегда является по-настоящему выгодной.

Поэтому, перед тем как сделать свой выбор, имеет смысл сделать небольшие вычисления, чтобы узнать итоговую сумму вклада при заданных условиях.

#2. Дисконтирование (помогает понять, что лучше: взять рассрочку или заплатить сейчас со скидкой)

Мы рассмотрели, какие бывают ставки и какие бывают способы начисления процентов. Если проценты выплачиваются в конце срока действия вклада, проценты называются простыми, если проценты выплачиваются с какой-то периодичностью, то такие проценты называются сложными.

Давайте решим обратную задачу. Допустим, мы знаем, сколько нам заплатят в будущем (например, нам кто-то пообещал платеж за какой-то продукт). Мы также знаем, какая сейчас процентная ставка. Как нам посчитать текущую цену этого продукта?

Как было сказано ранее, будущее значение суммы платежа будет равняться текущему значению, умноженному на единицу плюс процентная ставка. Если из этой формулы мы выразим текущее значение, то оно будет равняться будущему значению, деленному на единицу плюс процентная ставка.

Если проценты начисляются с какой-то периодичностью, то в общем виде формула выглядит так:

Давайте вернемся к задаче о том, какую премию лучше выбрать. В зависимости от способа премирования сумма выплат может отличаться. При этом не всегда очевидно, какой из способов предпочтительнее. Чтобы дать правильный ответ, необходимо решить математическую задачу. Предположим, у нас есть возможность взять в конце года 105 тысяч рублей при процентной ставке 5 процентов. Либо мы можем выбрать другой способ премирования, когда нам выплачивают по 50 тысяч рублей раз в полгода при той же процентной ставке.

Сравним эти два платежа. Для этого посчитаем, какое будет текущее значение для каждой из данных выплат. Воспользовавшись формулой для нахождения текущего значения, нам нужно продисконтировать 105 тысяч по ставке пять процентов (в данном случае T=1). Получаем 100 тысяч.

Чтобы найти текущее значение выплат через каждые полгода, мы должны 50 тысяч рублей (которые получим через полгода) продисконтировать по ставке два с половиной процента (потому что начисление происходит только в первые полгода. Строго говоря, ставка на 6 мес не равна половине годовой ставки. N(1+x)(1+x)=N(1+0.05) => x=2.4695% мы инвестируем на 6 мес, а потом опять на 6 и это идентично инвестиции на год), пять процентов годовых, деленные на два, плюс 50 тысяч полученные в конце года, которые мы дисконтируем по ставке 5 процентов. В результате подсчетов мы получаем цену первого платежа за полгода в размере 48780 рублей 49 копеек и второго платежа — 47619 рублей 5 копеек. Сумма ценностей составляет 96399 рублей 54 копеек.

Выгоднее получить премию в 105 тыс рублей, подождав дольше.

Например, когда вам предлагают купить автомобиль в рассрочку или заплатить полную сумму сейчас с какой-нибудь скидкой. Нужно взять будущую сумму, которую вы заплатите, привести к текущему значению, а затем сравнивать платежи, происходящие в один и тот же момент времени.

В таком случае сравнение будет корректным.

#3. Форвардные процентные ставки

Допустим, мы с вами договоримся о процентной ставке. Под эту процентную ставку я через год возьму у вас деньги в долг, которые верну через два года плюс процент. Какова должна быть в данном случае процентная ставка, чтобы она была справедливой? Распишем этот пример подробнее.

Либо положить деньги сразу по ставке r ₂ на два года.

На финансовом рынке существует правило отсутствия арбитража (No-Arbitrage Condition). Оно говорит о том, что если в конце срока мы получаем одинаковые выплаты, то для инструментов с одинаковым риском начальная сумма должна быть тоже одинаковая. Давайте распишем и это. Будущее значение первого варианта инвестиции FV ₁ будет равняться текущему значению, умноженному на сумму единицы и rT ₁ (будем считать, что у нас простое начисление процентов).

Из этого мы получаем следующее:

Формула получилась достаточно громоздкая. Давайте рассчитаем по этой формуле пример, а затем подумаем, что мы можем сделать, чтобы она выглядела проще.

Пусть процентные ставки у нас r ₁=4%; r ₂=6%. В таком случае имеем следующее:

Казалось бы странно, что ставка на два года равняется шести процентам, на год она равняется четырем процентам, а от года до двух мы получаем ставку более семи процентов. Объясняется это так. Поскольку в первый год у нас годовая ставка ниже чем на два года, в следующий год она должна быть выше, чем обе этих ставки. Это необходимо для того, чтобы компенсировать недостаток начисления процентов в первом году, и после реинвестирования можно было бы получить такую же сумму, как при инвестировании на два года по более высокой ставке. Такая ставка называется форвардной процентной ставкой.

Чтобы облегчить себе жизнь, давайте упростим эту формулу. Если мы будем использовать формулу непрерывного начисления процентов ( FV=PVe rT ), то тогда мы можем переписать условие отсутствия арбитража следующим образом:

Если мы возьмем логарифм от обеих сторон нашего равенства и сократим константы, мы получим:

Далее легко найти x:

Согласитесь, такую формулу для будущих процентных ставок использовать гораздо проще и удобнее.

Вы можете задать вопрос – а зачем такой странный продукт и кто им пользуется?

Представьте себе ситуацию, когда у вас или у вашей компании точно будет поступление средств через год. Сейчас вы бы хотели обезопасить себя от риска изменения процентных ставок. Вы понимаете, что через год процентная ставка может увеличиться и стать более выгодной, но также вы понимаете, что она может понизиться. И вам вполне комфортно с действующей на рынке форвардной процентной ставкой. Тогда вы можете заключить контракт, указав в нем, что на те деньги которые поступят в будущем через год, вы заключаете договор по заданной ставке. Ставка фиксируется, и вы больше не переживаете о том, как будут происходить изменения процентных ставок на рынке.

Обратите внимание, что форвардная процентная ставка ни в коем случае не является предсказанием будущей цены. Это абсолютно не значит, что процентные ставки будут равны 7,7% через год, когда мы окажемся в точке T₁. Они могут принимать какое угодно значение, и вот почему. В момент, когда мы рассчитываем форвардную процентную ставку из ставок, действующих на рынке, мы можем сказать, что эта ставка является ожиданием рынка относительно будущих цен. Но к моменту, когда мы перемещаемся в будущее, происходят новые события, добавляется новая информация, и рынок каким-то образом меняется. Поэтому процентные ставки через год не будут совпадать с форвардными ставками, рассчитанными на год сейчас.

Источник