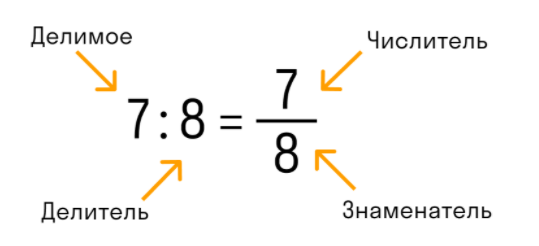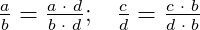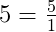что больше смешанная дробь или обычная

Сравнение десятичных дробей

Понятие десятичной дроби

Прежде чем мы расскажем, как сравнивать десятичные дроби, вспомним основные определения, виды дробей и разницу между ними.

Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это когда количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

Основные свойства

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

Правило сравнения десятичных дробей

Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.

Вот так с первой строчки раскрыли тему сравнения десятичных дробей 😜 Но это еще не все — едем дальше.

Алгоритм сравнения десятичных дробей

Применим правило на практике. Сравним десятичные дроби: 15,7 и 15,719.

Целую часть с целой частью: 15 = 15. Целые части равны.

Десятые с десятыми: 7 = 7. Десятые также равны.

Чтобы сравнить две десятичные дроби, нужно уравнять количество знаков после запятой (приписать к одной из них справа нули), затем отбросить запятую, и сравнить два натуральных числа.

Сравним 3,656 и 3,48.

Источник

Сравнение обыкновенных дробей

Сравнить две дроби — значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.

Сравнение дробей с одинаковыми знаменателями

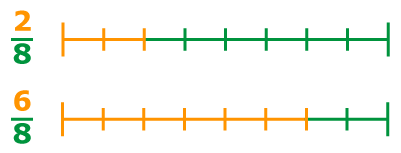
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

Пример. Дробь 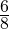больше чем дробь , потому что доли в обеих дробях одинаковы, но в первой дроби их больше, чем во второй.

Если изобразим единицу отрезком и разделим его на 8 долей, то легко увидеть, что дробь 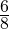больше :

Сравнение дробей с одинаковыми числителями

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.

Пример. Дробь 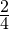больше чем дробь , потому что число долей в обеих дробях одинаково, но в первой дроби доли крупнее, чем во второй.

Изобразим две единицы в виде кругов, один разделим на 4 доли, второй на 6 долей. Теперь можно увидеть, что дробь 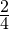больше :

Сравнение дробей с разными знаменателями и числителями

Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дроби: и .

Решение: приводим данные дроби к общему знаменателю:

Теперь сравниваем их по правилу сравнения дробей, у которых одинаковые знаменатели. Так как 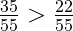, значит .

Приведём ещё один способ сравнения дробей с разными знаменателями и числителями. Рассмотрим сначала числовой пример.

Пример. Сравним дроби и .

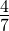
Решение: приводим данные дроби к общему знаменателю:

Решая данный пример можно заметить, что, после приведения дробей к общему знаменателю, задача сравнения свелась фактически к сравнению произведений

Так как 2 · 7 = 14, а 4 · 3 = 12, то

Значит, .

Теперь решим эту же задачу в общем виде, используя буквенную запись.

Пример. Пусть даны дроби и , где a и c — нуль или натуральные числа, b и d — натуральные числа. Приведём дроби к общему знаменателю:

Сравнение неправильной дроби с натуральным числом сводится к сравнению двух дробей.

Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби со знаменателем 1, затем их можно сравнить одним из двух способов: используя перекрёстное правило, либо привести дроби к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дробь с числом 5.

Решение: представим число 5 в виде дроби со знаменателем 1:

Приводим дроби к общему знаменателю:

Сравниваем числители, так как 11 Пример.

Онлайн калькулятор сравнения дробей

Источник

Как найти наибольшую и наименьшую дробь

Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.

Сравнение дробей с одинаковыми знаменателями.

Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.

Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.

Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:

Если мы до решаем эти дроби, то получим числа (frac = 5) и (frac = 2). Получаем, что 5 > 2

В этом и заключается правило сравнения дробей с одинаковыми числителями.

Рассмотрим еще пример.

Так как числители одинаковые, больше та дробь, где знаменатель меньше.

Пример №2:
Сравните правильную дробь с единицей?

Решение:
Любая правильная дробь всегда меньше 1.

Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?

Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби (frac ).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби (frac ).

Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.

Если у двух (или нескольких) дробей числитель одинаковый (то, что сверху черточки), то наименьшей дробью будет та, у которой знаменатель (то, что ниже черточки) наибольший, а наибольшей та, у которой знаменатель (то, что ниже черточки) наименьший.

В б наоборот – числители одинаковые, зато разные знаменатели. Представь себе пирог. Его разделили на столько частей, сколько написано внизу дроби. Из них взяли 31 часть. Чем на большее число частей поделили пирог, тем меньше часть (следовательно, находим где в знаменателе самое большое число – 53). Следовательно, пирог поделили на 53 части (маленькие) и из них взяли 31.

Ответы: 22/23 (самая большая в а)
31/53 (самая маленькая в б)

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали авторы-волонтеры.

Количество источников, использованных в этой статье: 5. Вы найдете их список внизу страницы.

Сравнивают дроби обычно для того, чтобы узнать, какая больше, а какая меньше. Чтобы сравнить дроби, вам нужно привести их к одному знаменателю, тогда дробь с большим числителем большая, а с меньшим — меньшая. Самое сложное — это уяснить, как делать так, чтобы дроби имели одинаковые знаменатели, но все не так сложно, как кажется. Мы расскажем, как все это делать. Читайте дальше!

Источник

Математические дроби – просто о сложном

В статье описаны математические дроби: основные виды дробей, их основное свойство, а также все операции, которые можно выполнять с дробями (сокращение, приведение, сравнение, сложение, вычитание, умножение и деление).

Дробь и ее виды

Правильная — дробь, у которой числитель меньше знаменателя (например, 1/5, 2/9).

Неправильная — дробь, у которой числитель больше или равен знаменателю (например, 7/2, 5/5).

Смешанная — дробь, записанная в виде целого числа и правильной дроби. Она представляет собой сумму этого числа и дроби. Любую неправильную дробь можно перевести в смешанную путем выделения целой части (например, 9/4 = 2 ¼).

Десятичная — дробь со знаменателем 10, 100, 1000 и т.д. (например, 7/10 или 0,7; 9/100 или 0,09). Десятичная дробь записывается в виде целой и дробной части, которые отделяются запятой.

Математические дроби: основное свойство

Если числитель и знаменатель умножить или разделить на одинаковое число (не ноль), то получится равная дробь. Например, 2/3 = 2*2 / 3*2 = 4/6

Сокращение дроби

Сокращение осуществляется с помощью основного свойства дроби (чтобы упростить ее вид).

Чтобы сократить математические дроби, нужно разделить числитель и знаменатель дроби на НОД.

НОД – это наибольший общий делитель (то есть максимальное число, на которое делится и числитель, и знаменатель). Например, для дроби 4/20 наименьшим общим делителем будет 4 (4/20 = 1/5).

Приведение дробей к общему знаменателю

Любые две дроби можно привести к общему знаменателю. Обычно дроби приводят к наименьшему общему знаменателю (НОК) – минимальное число, которое делится на каждый знаменатель.

Например, для дробей 1/4 и 1/3 общий знаменатель общий знаменатель равен 12, для дробей 1/6 и 1/3 общий знаменатель будет 6).

Для приведения дроби к общему знаменателю нужно:
1. Найти общий знаменатель – НОК (для дробей 1/6 и 1/9 общий знаменатель будет равен 18);
2. Найти множитель для каждой дроби – разделить общий знаменатель на знаменатель исходной дроби (для дроби 1/6 множитель будет равен 3 (18:6=3), для дроби 1/9 – 2 (18:9=2)).
3. Умножить числитель дроби на множитель (для дроби 1/6 получаем 1*3/6*3=3/18, для дроби 1/9 получаем 2*1/2*9=2/18)

Преобразование неправильной дроби в смешанную дробь и обратно

Любую неправильную дробь можно перевести в смешанную (рассмотрим на примере 14/3).
Для перевода необходимо выполнить деление числителя на знаменатель с остатком (14 разделить на 3 равно 4 и остаток 2): получавшаяся целая часть от деления (число 4) – целая часть дроби, остаток от деления (число 2) – числитель правильной дроби. Получаем число 4 2/3.
На примере пирога: каждый пирог разрезан на 3 части и всего есть 14 кусочков. Получаем, что 12 кусочков составляют 4 целых пирога и еще остается два кусочка).

Для перевода смешанной дроби в неправильную необходимо (рассмотрим на примере 4 2/3):
для получения числителя целую часть дроби умножить на знаменатель и прибавить исходный числитель (4 умножить на 3 и прибавить 2, получим 14); знаменатель оставить прежним (число 3).
На примере пирога: есть 4 целых пирога, разрезанных на 3 части, и еще 2 кусочка из трех; получаем 12 кусочков из пирогов, разрезанных на три части, и 2 кусочка из пирога, разрезанного на три части. Итого, получаем 14 кусочков пирогов, каждый из которых разрезан на три части.

Математические дроби: сравнение

Если сравнивать две математические дроби с одинаковыми знаменателями, то больше та дробь, числитель которой больше (например, 5/6 > 1/6, то есть пять частей из шести будет больше, чем одна часть из шести).

Если сравнивать две математические дроби с одинаковыми числителями, то больше та дробь, знаменатель которой меньше (например, 1/2 > 1/3, то есть 1/2 часть пирога будет больше, чем 1/3).

Чтобы сравнить две обыкновенные дроби, следует привести дроби к общему знаменателю и сравнить числители получившихся дробей (например, для сравнения 3/4 и 5/6 нужно привести дроби к общему знаменателю; получаем 9/12

Для отправки комментария вам необходимо авторизоваться.

Источник

Сравнение смешанных чисел: правила, примеры, решения.

В этой статье речь пойдет про сравнение смешанных чисел. Сначала мы разберемся, какие смешанные числа называются равными, а какие – неравными. Дальше мы приведем правило сравнения неравных смешанных чисел, которое позволяет выяснить, какое число больше, а какое – меньше, и рассмотрим примеры. Наконец, мы остановимся на сравнении смешанных чисел с натуральными числами и обыкновенными дробями.

Навигация по странице.

Равные и неравные смешанные числа

Сначала нужно знать, какие смешанные числа называются равными, а какие – неравными. Дадим соответствующие определения.

Равные смешанные числа – это смешанные числа, у которых равны и целые части, и дробные части.

Иными словами, два смешанных числа называются равными, если их записи полностью совпадают. Если же записи смешанных чисел отличаются, то такие смешанные числа называют неравными.

Неравные смешанные числа – это смешанные числа, записи которых отличаются.

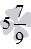
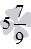
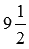
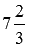
Озвученные определения позволяют с одного взгляда определить, равны ли данные смешанные числа или нет. Например, смешанные числа и равные, так как их записи полностью совпадают. Эти числа имеют равные целые части и равные дробные части. А смешанные числа и — неравные, так как они имеют неравные целые части. Другими примерами неравных смешанных чисел являются и , а также и .

Иногда возникает необходимость выяснить, какое из двух неравных смешанных чисел больше другого, а какое – меньше. Как это делается, рассмотрим в следующем пункте.

Сравнение смешанных чисел

Для примера, сравним смешанное число и смешанное число , представив их в виде неправильных дробей. Имеем и . Так сравнение исходных смешанных чисел сводится к сравнению дробей с разными знаменателями и . Так как , то .

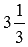
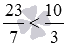
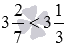
Сравнение смешанных чисел через сравнение равных им дробей является не лучшим решением. Гораздо удобнее использовать следующее правило сравнения смешанных чисел: больше то смешанное число, целая часть которого больше, если же целые части равны, то больше то смешанное число, дробная часть которого больше.

Рассмотрим, как происходит сравнение смешанных чисел по озвученному правилу. Для этого разберем решения примеров.

Сравните смешанные числа и .

Целая часть смешанного числа меньше целой части смешанного числа ( 5 смотрите сравнение натуральных чисел), поэтому .

.

Какое из смешанных чисел и больше?

Целые части сравниваемых смешанных чисел равны, поэтому сравнение сводится к сравнению дробных частей и . Так как , то . Таким образом, смешанное число больше, чем смешанное число .

.

Сравнение смешанного числа и натурального числа

Разберемся, как сравнить смешанное число и натуральное число.

Справедливо такое правило сравнения смешанного числа с натуральным числом: если целая часть смешанного числа меньше данного натурального числа, то смешанное число меньше данного натурального числа, а если целая часть смешанного числа больше или равна данному смешанному числу, то смешанное число больше данного натурального числа.

Разберем примеры сравнения смешанного числа и натурального числа.

Сравните числа 6 и .

.

Целая часть смешанного числа 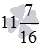меньше числа 34 ( 11 ), поэтому .

Выполните сравнение числа 5 и смешанного числа .

.

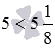
Сравнение смешанного числа и обыкновенной дроби

Сначала скажем про сравнение смешанного числа и правильной дроби. Любая правильная дробь меньше единицы (смотрите правильные и неправильные дроби), следовательно, любая правильная дробь меньше любого смешанного числа (так как любое смешанное число больше 1 ).

Приведем пример: смешанное число больше любой правильной дроби, в частности, смешанное число больше дроби .

Сравнение смешанного числа и неправильной дроби можно свести либо к сравнению двух дробей, либо к сравнению двух смешанных чисел. Для этого в первом случае смешанное число нужно представить в виде неправильной дроби, во втором случае – неправильную дробь представить в виде смешанного числа. Второй способ предпочтительнее.

Покажем два способа решения.

.

Источник