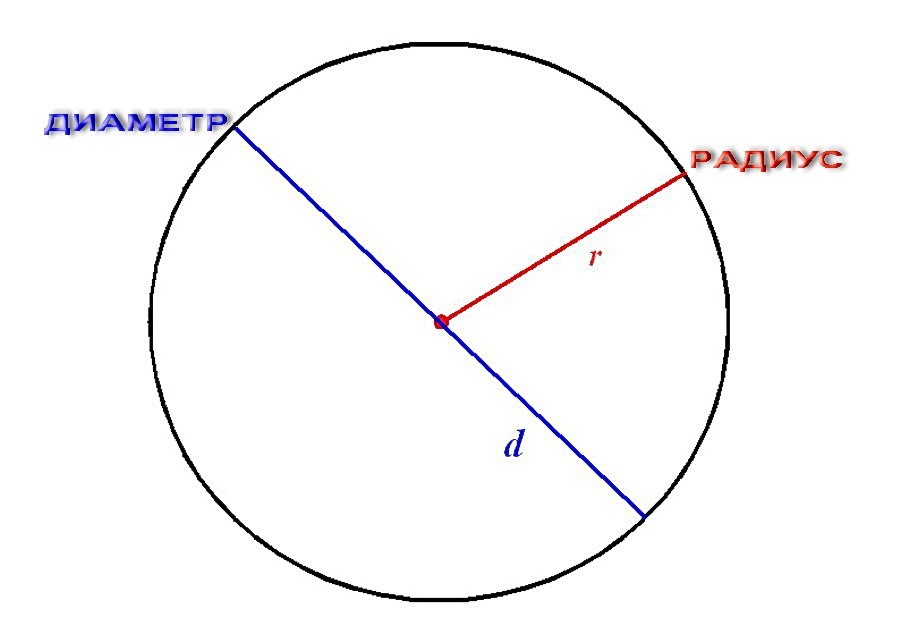
что больше радиус или диаметр окружности
Радиус и диаметр окружности
Окружность — это фигура в геометрии, которая состоит
из множества точек, расположенных на одинаковом
расстоянии от заданной точки (центра окружности).
Радиус окружности — это отрезок, который соединяет
центр окружности с какой-либо точкой окружности.
Диаметр окружности — это отрезок, который соединяет
две любые точки окружности, причем сам отрезок
должен проходить через центр окружности
Eсли от центра окружности провести
отрезки ко всем точкам окружности, то они будут иметь
одинаковую длину, то есть равны. В математике
такие отрезки называют радиусами.
Все радиусы окружности, как и диаметры окружности,
равны между собой, имеют одинаковую длину.
На рисунке выше изображена окружность, с центром в точке O.
OA = OB = OC — радиусы окружности;
BC = CO + OB — диаметр окружности;
Радиус окружности принято обозначать маленькой либо большой буквой, r или R.
Диаметр окружности обозначают буквой D.
Диаметр окружности условно состоит из двух
радиусов и равен длинам этих радиусов.
Длину радиуса окружности можно найти через диаметр окружности.
Для этого достаточно разделить на два длину диаметра окружности,
получившееся число и будет радиусом.
Формула радиуса окружности через диаметр:
Формула диаметра окружности через радиус:
Также, окружность, может быть вписанной в фигуру, описанной
около фигуры; или вообще может быть не вписана и не описана.
Формула радиуса окружности зависит от того находится фигура
внутри окружности, или окружность находится около фигуры.
Существует радиус вписанной окружности
и радиус описанной окружности.
Формулы радиуса вписанной и радиуса описанной окружностей
зависят в первую очередь от геометрической фигуры.
Радиус вписанной окружности — это радиус окружности,
которая вписана в геометрическую фигуру.
Радиус описанной окружности — это радиус окружности,
которая описана около геометрической фигуры.
Всё про окружность и круг
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
что такое радиус и диаметр?
Свернуть
WLE Austria Logo (no text).svgФотоконкурс «Вики любит Землю»: Ваш взгляд на российские природные памятники!
Диаметр
[править | править вики-текст] Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 февраля 2016; проверки требуют 12 правок.
Диа́метр в изначальном значении термина — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.
Содержание [убрать]
1Диаметр геометрических фигур
2Символ диаметра
2.1Сопряжённые диаметры эллипса и гиперболы
2.2Сопряжённые диаметры эллипса
2.3Сопряжённые диаметры гиперболы
3Вариации и обобщения
4Некоторые окружности, построенные в треугольнике на одном отрезке, как на диаметре
5См. также
6Литература
Диаметр геометрических фигур [править | править вики-текст]
Радиус (r) и диаметр (d) окружности
Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.
Символ диаметра [править | править вики-текст]
Символы со сходным начертанием: Ø · ∅
Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или ⌀). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» в Windows, программу «Таблица символов Юникода» (gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. Специализированные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов %%c (буква c — латинская) или \U+2205 в текстовой строке.
Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.
Сопряжённые диаметры эллипса и гиперболы [править | править вики-текст]
Сопряжённые диаметры эллипса [править | править вики-текст]
Пара сопряжённых диаметров эллипса. Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу и четыре таких касательных ко всем четырем концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм
Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
На рисунке представлена пара сопряженных диаметров (красный и синий). Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырем концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зеленые линии на рисунке).
Расстояния r_1 и r_2 от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
Радиус эллипса в данной точке (расстояние от его
Диаметр и радиус — что это такое?
В жизни человек часто сталкивается с понятием окружность. Все едят с круглых тарелок, грызут круглые яблоки, катаются на велосипеде или ездят на транспорте с круглыми колесами и просто видят круглое солнце.
Понятия радиус и диаметр
Немногие задумываются, что на самом деле круг – очень сложная замкнутая фигура. Она состоит из главной точки (так называемый центр), а также из множества точек, которые идут от этого центра. Расстояние от центральной точки до окружности называют радиус. Чаще всего это понятие обозначается букой «R».
Если соединить две противоположные друг другу точки окружности и провести между ними линию, то она и будет диаметром. Диаметр обозначают символом «Ø». То есть радиус всегда будет равен половине диаметра.
Как использовать эти понятия в жизни
Вообще с этими понятиями знакомы практически все, кто учил геометрию в школе. Взрослые тоже часто сталкиваются с ними, когда помогают детям делать домашнее задание или просто проверяют его.
Также эти понятия очень часто используются в черчении, к примеру, в архитектуре, когда планируется сделать круглое окно, арку или другую круглую деталь.
В ландшафте тоже не обойтись без радиуса и диаметра, ведь именно они позволят поделить круг на несколько частей, создав яркие цветочные композиции. Последние будут не только радовать глаза, но и помогут отвлечь внимание гостей от грядок с овощами.
Во время конструирования одежды тоже часто встречаются понятия радиус и диаметр. Например, когда шьют шляпы, юбки или круглые накладные воротники.
Понятия диметр и радиус часто используются в программировании и создании сайтов. К примеру, многие создают программы для коррекции кругов (последние используются в разных сферах).
Важно обратить внимание, что понятия диаметр и радиус касаются не только круга. Круг – это фигура, которая лежит на определенной плоскости. Но в геометрии фигуры не всегда лежат на плоскости, некоторые находятся в пространстве. И понятия круг в пространстве вообще не существует, в нем используются объемные фигуры, например, эллипс, цилиндр, конус или шар. Для вычисления объема всех этих фигур тоже понадобится определять диаметр и радиус.
Другие понятия
Существует еще несколько понятий, которые могут пригодиться тем, кто работает с диаметром или радиусом:
Все перечисленные выше понятия пригодятся не только тем, кто учит геометрию, но и тем, кто имеет дело с кругами в других сферах. В математике существует несколько формул, которые помогут выяснить величину любого из описанных выше понятий по заданным параметрам.
Радиус и диаметр окружности — определение двух отрезков
На практике в жизни с окружностью сталкивается каждый человек. Это может быть обруч, который крутят на уроке физкультуры либо на занятиях фитнеса, а также арена цирка либо просто украшение на пальце — кольцо. Радиус и диаметр окружности — взаимосвязанные математические понятия, которые необходимо выучить детям в школьной программе еще в начальной школе.
Определения понятий
Чтобы изобразить фигуру, достаточно обвести контур карандашом вокруг круглого предмета либо начертить при помощи циркуля. На месте прокола циркуля ставят точку, что и будет центром окружности.
Окружность — геометрическое место точек плоскости, в котором длина от точек к центру одинаковая. По-другому можно описать определение, что это замкнутая кривая, в которой править будут равные отрезки, проведенные от центра до краев фигуры. Круг — часть плоскости, которая ограничена окружностью.
Если поставить точку на окружности и соединить ее с центром, в результате получится отрезок. Таких отрезков можно нарисовать не один, сколько точек на окружности поставить — столько и будет таких отрезков, то есть бесчисленное количество.
Отрезок, который равен расстоянию от центра до границ окружности имеет название радиуса. Этот термин с латинскими корнями и в переводе означает луч либо спица колеса.
Первый раз о термине заговорили в 1569 году, и примерно через 100 лет он стал общепринятым. И не удивительно, так как в обиходе люди часто говорят, к примеру, «пожар в радиусе 10 км уничтожил все», «в радиусе 5 м нет видимости» и так далее.
Диаметром называется отрезок, который соединяет 2 точки окружности и проходит обязательно через центр круга. Такой отрезок делит круг на 2 части. По-другому — хорда, которая проходит через центр круга. Этот отрезок самый больший, который можно изобразить в круге, что и будет отличаться от других отрезков. Их можно изобразить в фигуре бесконечное число.
Обозначения и свойства
Понятия имеют принятые обозначения. Буквой d обозначают диаметр (в некоторых источниках обозначается перечеркнутой буквой о), а r — радиус. Для измерения используют:
Диаметр состоит из 2 радиусов, а это значит, если необходимо узнать, чему равен радиус, необходимо длину диаметра разделить напополам. То есть разница между ними в 2 раза. Не всегда два радиуса образуют диаметр: только при условии, если они находятся на одной прямой.
Для решений задач можно использовать формулу: d =2*r. Естественно, формула работает в обратном направлении, она будет выглядеть следующим образом: r = d/2.
Дано: r =80 мм, определить, на сколько сантиметров диаметр длиннее. Для решения задачи используют формулу d=2*r. Но для начала необходимо перевести миллиметры в сантиметры. 80 мм=8 см. Далее d=2*8=16 см. Чтобы вычислить отличие, необходимо 16−8=8 см. Ответ — на 8 см длиннее.
Дополнительные сведения
Если в окружности провести 2 радиуса, то в результате круг будет разделен на 2 части, которые называются секторами. Отрезки образуют центральный угол.