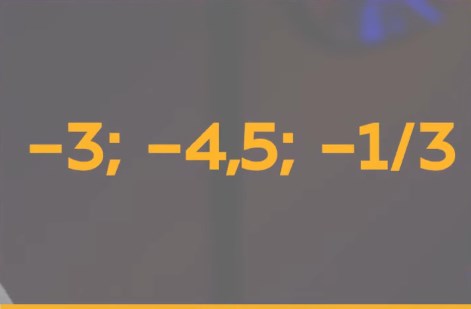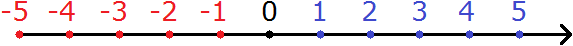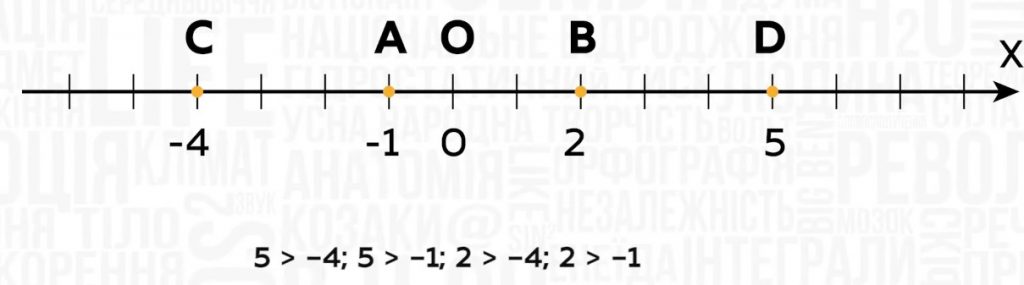что больше ноль или отрицательное число

0 положительное или отрицательное целое число?

Впоследствии, какой тип набора отрицательных целых чисел?

Ноль не считается ни положительным, ни отрицательным. Действительные числа можно визуализировать на горизонтальной числовой строке с произвольной точкой, выбранной как 0, с отрицательными числами слева от 0 и положительными числами справа от 0.

Какое наибольшее отрицательное целое число?

Какое наименьшее отрицательное целое число?

(c) Наименьшее отрицательное целое число равно -1.

Ноль больше любого отрицательного целого числа?

0 стоит слева от всех натуральных чисел. … 0 находится справа от всех отрицательных целых чисел. Так, 0 больше любого отрицательного целого числа.

Что такое отрицательная бесконечность?

Есть ли в математике отрицательный ноль?

Каковы примеры ненастоящих чисел?

Какие есть примеры целых чисел?

Является ли одновременно целым и целым числом?

Какие бывают типы целых чисел?

Целые числа бывают трех типов:

Какое отрицательное наибольшее отрицательное целое число?

Наибольшее отрицательное целое число -1.

Что больше в отрицательных числах?

В числовой строке отрицательные числа слева от нуля. –5 меньше 4, потому что –5 находится слева от 4 в числовой строке. –1 больше –3, потому что –1 находится справа от –3 на числовой прямой.

Какое наибольшее отрицательное целое число?

Какое число является наименьшим целым числом?

Какое правило умножения отрицательных чисел?

Вы также должны обращать внимание на знаки при умножении и делении. Следует помнить два простых правила: когда вы умножаете отрицательное число на положительное, тогда продукт всегда отрицательный. Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда будет положительным.

Какое наименьшее целое число?

Какое наибольшее отрицательное целое число?

Наибольшее отрицательное целое число -1.

Что больше любого отрицательного целого числа?

0 больше любого отрицательного целого числа.

Что является самым большим положительным или отрицательным?

Источник

Положительные и отрицательные числа. Число 0

Отрицательные числа появились в Древнем Китае примерно во II веке до нашей эры из-за жизненных потребностей людей. Отрицательные числа тогда толковали как долг, а положительные как имущество.

Если на банковском счету есть деньги, то сумма денег положительная. Но если со счета снимают сумму больше, чем текущий остаток денег, то сумма на счете становится отрицательной.

К примеру, на банковском счету пять тысяч рублей (5000 руб). Это число положительное. Если снимают сумму шесть тысяч рублей (6000 руб), то уже есть долг перед банком 1000 рублей. Говорят, на счету минус тысяча рублей (–1000 руб). Пишут: минус тысяча рублей.

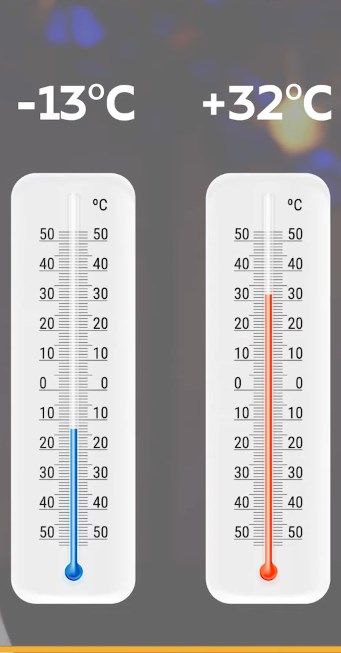
Столбик термометра, изображенный на первом рисунке, указывает на тринадцатое деление, расположенное ниже нуля. В таком случае говорят, что температура равна минусу тринадцать градусов. Можно сказать, что термометр показывает тринадцать градусов ниже нуля или тринадцать градусов мороза.

На втором рисунке термометр показывает тридцать два градуса выше нуля. В таком случае говорят, что температура равняется плюс тридцать два градуса, или тридцать два градуса тепла.

Помни, что число больше нуля является положительным, а число меньше нуля – отрицательным. Число 0 – ни положительное, ни отрицательное.

Положительные числа обозначаются с помощью знака «+» или не имеют этого знака перед собой. Например, +32ºС (плюс тридцать два градуса по Цельсию). +15 (плюс пятнадцать) и 15 (пятнадцать) – это одно и то же число, записанное разными способами. Итак, натуральные и дробные числа, которые вы изучали раньше, будем называть положительными.

Если число отрицательное, то перед ним стоит знак «-«. К примеру, на банковском счету минус тысяча рублей (–1000 руб). Числа –3 (минус три); – 4,5 (минус четыре целых пять десятых); –1/3 (минус одна третья) отрицательные.

Если одно число положительное, а второе – отрицательное, то о таких числах говорят, что они имеют разные знаки. Сорок пять и минус тринадцать – числа с разными знаками. А если оба числа положительные или оба отрицательные, то говорят, что они имеют одинаковые знаки. Двадцать четыре и пятьдесят шесть. Минус три и минус пять целых и восемь десятых – числа с одинаковыми знаками

Решим задачу 1
Какие из приведенных чисел являются положительными, а какие – отрицательными:
23; – 65; –4,9; 5,76; 0; –7 1/7
Решение
Положительные: 23; 5,76
Отрицательные: – 65; –4,9; –7 1/7
Напомним, что ноль ни положительное, ни отрицательное число.

Решим задачу 2

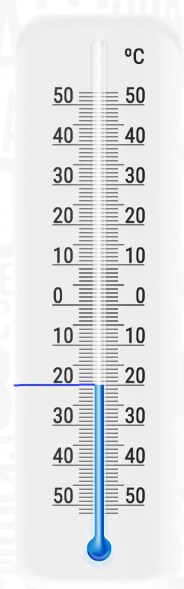
Какую температуру будет показывать термометр, изображенный на рисунке, если:

Решение

Решим задачу 3

Леночка вошла в лифт на пятом этаже, проехала три этажа и вышла из лифта.
На каком этаже она вышла?
Сколько вариантов ответа?

Решение

Источник

Математика

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

В кабинет к шестиклассникам вошла Наталья Ивановна, и сообщила,что завтра в школе состоится выступление цирковой труппы, стоимость билета составляет 50 рублей. Желающие посетить представление, должны завтра принести деньги на приобретение билета. Ваня и Игнат очень хотели посмотреть выступление, договорились приобрести билеты. Однако, Игнат забыл деньги дома. Мальчик очень огорчился. Наталья Ивановна заметила грустного ученика и предложила купить билет вместо него, с условием, что мальчик принесет забытую купюру завтра. Друзья с радостью пошли на представление.

Сравнение положительных чисел с нолем

Чтобы не испытывать трудностей при выполнении сравнения положительных чисел и нуля, давайте рассмотрим задачу.

У Марины в кармане было четыре конфеты, а в Наташином кармашке лежало 0 конфет. Подумайте и объясните, у кого из девочек имелось большее количество конфет.

Изучив условие задачи, мы понимаем, что для ответа на главный вопрос задачи нужно выполнить сравнение количества Марининых сладостей с количеством сладостей, имеющихся у Натальи, то есть 4 и 0.

Давайте определим, к каким числам можно отнести значение четыре? К положительным или отрицательным?

Вспомним определение положительного:

Положительными числами называют числа со знаком +.На письме, не принято ставить знак «плюс» перед положительными числами. Считается, что если перед числом не стоит знак «минус», то число является положительным.

Исходя из определения, рассматриваемое значение считается положительным.

Переходим ко второму числу: 0.

Обязательно нужно понимать, что такое 0.

0 является целым числом, но при этом, не обозначает количество предметов.

Если будем рассматривать ноль в обычной жизни, то можно сказать иначе: 0 = «ничего».

в кассе 0 рублей = касса пуста, денег нет;

улов дедушки составил 0 рыб = дедушка ничего не поймал;

мальчик вынес во двор 0 игрушек = мальчик не вынес во двор игрушки.

Делаем вывод, что у Наташи не было конфет, а у Марины было 4 леденца.

Теперь можно выполнить сравнение положительного числа 4 с числом 0.

Даже ребенок понимает, что четыре конфетки больше, чем ничего или 0.

Из рассмотренного пояснения следует:

любое положительное число всегда будет больше, чем ноль!

Сравнение отрицательных чисел с нулем

Теперь, давайте разберемся, как сравнить отрицательное число с нулем. Для начала вспомним, какие числа называют отрицательными.

Чтобы разобрать данную ситуацию, нужно определить, в какой из дней на улице будет теплее, следовательно, температура воздуха будет выше (больше). Для этого необходимо сравнить прогнозируемую температуру четверга и пятницы. По условию, в четверг 0˚C, а в пятницу-2˚C. Получается, что нам нужно сравнить отрицательное число и ноль. А как это правильно сделать? В математике существует правило, которое говорит:

Ноль всегда будет больше любого отрицательного числа.

Исходя из рассмотренного правила, сравним предполагаемые показатели термометра в указанные дни:

0>-2 – ноль больше, чем минус два.

Теперь, мы можем сказать, что в четверг температура воздуха будет больше (выше), а значит, именно в этот день будет теплее.

Выполнять сравнение цифровых записей со знаком «минус» и ноля очень просто, главное помнить, что ноль всегда больше любого отрицательного числа!

Сравнение положительных и отрицательных чисел

Как выполнять сравнение положительных и отрицательных чисел с нолем мы уже знаем, а как же сравнивать числа со знаками «плюс» и «минус» между собой? Математика предусмотрела и этот вариант сравнения чисел. Существует правило сравнения положительных и отрицательных чисел.

При сравнении положительного и отрицательного числа, большим всегда будет положительное число.

Рассмотрим на примере.

Сравнение отрицательных чисел

Теперь давайте рассмотрим, как правильно сравнивать числовые значения со знаком «минус».

Если возникла необходимость сравнить отрицательные числа, то нужно помнить простое правило сравнения отрицательных чисел.

Из двух отрицательных чисел большим будет то число, модуль которого меньше.

Разберем на примере.

Вначале, кажется, что сравнивать такие числа очень просто и с этим заданием справится даже первоклассник. Но на самом деле, для выполнения сравнения данных значений необходимо соблюдать следующий алгоритм:

Модуль любого числа всегда имеет только положительное значение.

Для положительного числа модуль равен этому числу:
3=|3|, 24=|24|.

Так как перед каждой записью стоит знак минус, то числа считаются отрицательными, а модуль отрицательного числа равен противоположному числовому значению самого числа.

Рассмотренное правило, говорит о том, что большим будет то число, которое имеет меньший модуль.

При выполнении сравнения значений со знаком минус важно помнить, большим будет то число, модуль которого меньше!

Сравнение числовых значений с использованием горизонтальной координатной прямой

Ну а теперь, рассмотрим еще одни способ сравнения цифровых записей с разными знаками.

Давайте начертим координатную прямую. Для этого, вспомним, что представляет собой координатная прямая.

Координатная прямая – прямая линия, имеющая направление, точку начала отсчета и единичный отрезок.

Отметим на прямой точки A(-4), C(-2), B(2),D(3).

Помни!Точки с положительным значением координаты расположены справа от точки начала отсчета, точки с отрицательным значением координаты находятся слева от точки начала отсчета.

И теперь, с помощью горизонтальной координатной прямой давайте рассмотрим математическое действие – сравнение чисел.

Мы знаем, что точки с положительными координатами, расположились справа от точки начала отсчета, а с отрицательными слева. На координатную прямую нанесены точки B и D, имеющие координаты со знаком «плюс». Сравним координаты данных точек.

Используя рассмотренное правило, делаем вывод, что точка с любой положительной координатой, находится на координатной прямой, правее точки начала отсчета, а значит, имеет большее числовое значение.

То есть, ноль всегда меньше любого положительного числа.

Любая точка, имеющая отрицательное значение координаты, всегда будет расположена левее точки 0, следовательно, любая числовая запись со знаком «минус» всегда меньше 0.

Сравнивать очень просто и интересно, главное запомнить простые правила сравнения и верно использовать их при выполнении заданий!

Источник

Отрицательные числа

Отрицательные числа — это числа со знаком минус (−), например −1, −2, −3. Читается как: минус один, минус два, минус три.

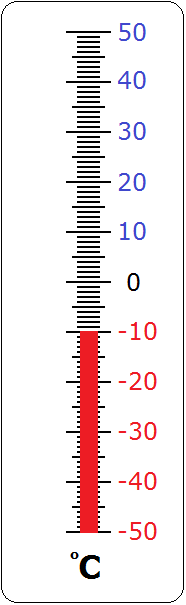
Примером применения отрицательных чисел является термометр, показывающий температуру тела, воздуха, почвы или воды. В зимнее время, когда на улице очень холодно, температура бывает отрицательной (или как говорят в народе «минусовой»).

Например, −10 градусов холода:

Обычные же числа, которые мы рассматривали ранее такие как 1, 2, 3 называют положительными. Положительные числа — это числа со знаком плюс (+).

При записи положительных чисел знак + не записывают, поэтому мы и видим привычные для нас числа 1, 2, 3. Но следует иметь ввиду, что эти положительные числа выглядят так: +1, +2, +3.

Координатная прямая

Координатная прямая это прямая линия, на которой располагаются все числа: и отрицательные и положительные. Выглядит следующим образом:

Здесь показаны только числа от −5 до 5. На самом деле координатная прямая бесконечна. На рисунке представлен лишь её небольшой фрагмент.

Числа на координатной прямой отмечают в виде точек. На рисунке жирная чёрная точка является началом отсчёта. Начало отсчёта начинается с нуля. Слева от начала отсчёта отмечают отрицательные числа, а справа — положительные.

Каждая точка на координатной прямой имеет своё имя и координату. Имя — это любая латинская буква. Координата — это число, которое показывает положение точки на этой прямой. Проще говоря, координата это то самое число, которое мы хотим отметить на координатной прямой.

Например, точка А(2) читается как «точка А с координатой 2« и будет обозначаться на координатной прямой следующим образом:

Здесь A — это имя точки, 2 — координата точки A.

Пример 2. Точка B(4) читается как «точка B с координатой 4« и будет обозначаться на координатной прямой так:

Пример 3. Точка M(−3) читается как «точка M с координатой минус три» и будет обозначаться на координатной прямой так:

Здесь M — это имя точки, −3 — координата точки M.

Точки можно обозначать любыми буквами. Но общепринято обозначать их большими латинскими буквами. Более того, начало отчёта, которое по другому называют началом координат принято обозначать большой латинской буквой O

Легко заметить, что отрицательные числа лежат левее относительно начала отсчёта, а положительные числа правее.

Сравнение отрицательных и положительных чисел

Правило 1. Любое отрицательное число меньше любого положительного числа.

Например, сравним два числа: −5 и 3. Минус пять меньше, чем три, несмотря на то, что пятёрка бросается в глаза в первую очередь, как цифра большая, чем три.

Связано это с тем, что −5 является отрицательным числом, а 3 — положительным. На координатной прямой можно увидеть, где располагаются числа −5 и 3

«Минус пять меньше, чем три»

Правило 2. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой.

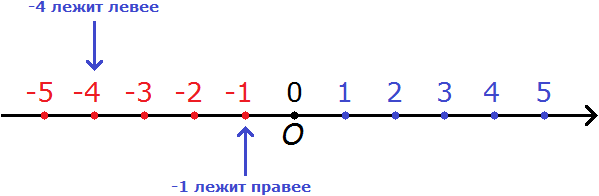
Например, сравним числа −4 и −1. Минус четыре меньше, чем минус единица.

Связано это опять же с тем, что на координатной прямой −4 располагается левее, чем −1

Правило 3. Ноль больше любого отрицательного числа.

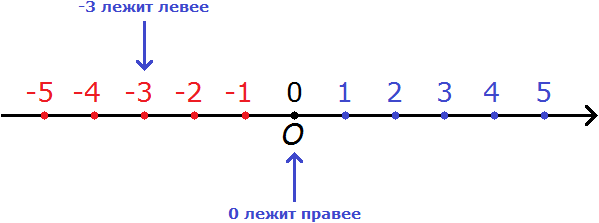
Например, сравним 0 и −3. Ноль больше, чем минус три. Связано это с тем, что на координатной прямой 0 располагается правее, чем −3

Ноль больше, чем минус три

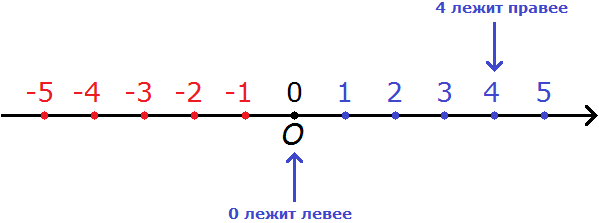
Правило 4. Ноль меньше любого положительного числа.

Например, сравним 0 и 4. Ноль меньше, чем 4. Это в принципе ясно и так. Но мы попробуем увидеть это воочию, опять же на координатной прямой:

Источник

Сравнение положительных и отрицательных чисел

Из этого урока вы научитесь сравнивать рациональные числа.

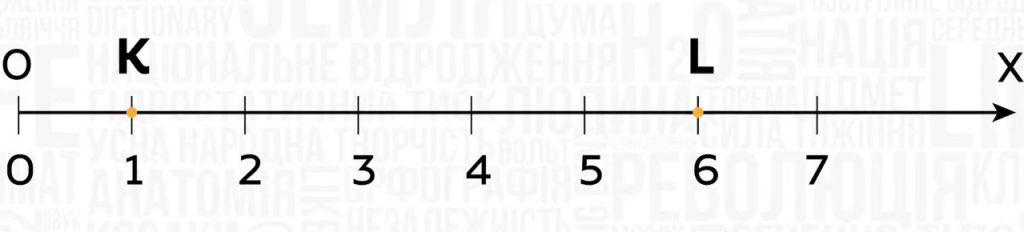
На координатном луче точка L с координатой 6 расположена правее точки К с координатой 1. Поэтому 6 > 1.

Следовательно, большим из двух чисел есть число, расположенное на координатной прямой правее.

Помни, что на координатной прямой любое отрицательное число расположено левее любого положительного числа. Поэтому любое отрицательное число всегда меньше любого положительного числа.

Например, пять больше минус четыре; пять больше минус один; два больше минус четыре; два больше минус один.

На рисунке точка А с координатой минус один лежит правее (ближе нуля) от точки С с координатой минус четыре, поэтому минус один больше минус четыре. Заметим, что модуль минус один меньше модуля минус четыре. Следовательно, из двух отрицательных чисел больше то, модуль которого меньше.

На координатной прямой число 0 расположено левее любого положительного числа и правее любого отрицательного числа.
Следовательно, любое положительное число больше нуля. Записывают в виде неравенства: a > 0.

Любое отрицательное число меньше нуля. Записывают в виде неравенства: a ≥ 0. Читают: «а больше или равно нулю».
Если а – не положительное число (т.е. отрицательное или ноль), то пишут а ≤ 0. Читают: «а меньше или равно нулю»

Используя эти обозначения запишем свойство модуля числа а так:

модуль «а» равен «а», если «а больше или равен нулю»;
модуль «а» равен «-а», если «а меньше нуля».

Решаем задачи

Задание 1:

Какая из двух точек расположена справа от другой:

Решение:

Задание 2:

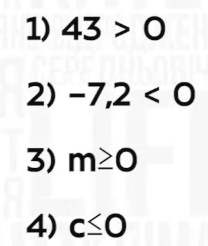
Запишите в виде неравенства утверждение:

Решение:

любое положительное число больше нуля, следовательно, 43 > 0;

поскольку «С» – не положительное число, то «С» ≤ 0.

Задание 3:

Решение:

По условию следует записать числа от наибольшего к наименьшему.

Наибольшим из чисел, расположенным на координатной прямой справа, является число 7,23. Затем 2; 0,2; 0.

Поскольку среди отрицательных чисел наибольшее число то, у которого модуль наименьший, поэтому сравним модули отрицательных чисел:

Ответ:

Вы научились сравнивать рациональные числа. Для закрепления этого навыка выполните задания Онлайн тренажера Сравнение целых чисел

Источник