число грэма для чего нужно

зачем нужно число Грэма?

Самым большим числом, когда-либо применявшимся в математическом доказательстве, является предельная величина, известная как число Грэма (Graham’s number), впервые использованная в 1977 года в доказательстве одной оценки в теории Рамсея. Оно связано с бихроматическими гиперкубами и не может быть выражено без особой 64-уровневой системы специальных математических символов, введённых Кнутом в 1976 году.
Термин «гугол» не имеет серьёзного теоретического и практического значения. Каснер предложил его для того, чтобы проиллюстрировать разницу между невообразимо большим числом и бесконечностью, и с этой целью термин иногда используется при обучении математике.

Интересные факты;
Гугол больше, чем количество частиц в известной нам части Вселенной, которых насчитывается, по разным оценкам от 1079 до 1081.

Сторона куба, состоящего из гугола атомов алюминия, составит около 58 млн световых лет.

Гугол «приблизительно» равен факториалу числа 70. Имеет только два простых делителя — 2 и 5. Двоичное представление гугола состоит из 333 бит.

Используя официально принятую в России, США и ряде других стран систему именования больших чисел (см. http://sizes.org.ru/numbers/large/ или en:Names of large numbers), гугол можно представить как десять дуотригинтиллионов.

В двоичной системе счисления гугол записывается следующим образом:
1 0010 0100 1001 1010 1101 0010 0101 1001 0100 1100 0011 0111 1100 1110 1011 0000 1011 0010 0111 1000 0100 1100 0100 1100 1110 0000 1011 1111 0011 1000 1010 1100 1110 0100 0000 1000 1110 0010 0001 0001 1010 0111 1100 1010 1010 1011 0010 0100 0011 0000 1000 1010 1000 0010 1110 1000 1111 0001 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000

В 16-ричной системе:
1249AD2594C37CEB0B2784C4CE0BF38ACE408E211A7CAAB24308A82E8F1000000000000000000000000

Повторение Большого взрыва возможно, однако вероятность этого события крайне мала. Ученые высчитали это число, однако написать его практически невозможно.

Это число выглядит как десятичная дробь, у которой после запятой и перед единицей стоит 100 миллионов триллионов триллионов триллионов триллионов нулей.

Источник

Самое большое число в мире, которое что-то обозначает

Миллион = 1 000 000 = 10⁶

Представить миллион чего-то мы тоже можем:

С миллионами чего-либо мы сталкиваемся довольно часто и так:

— миллион секунд — это всего-навсего 11,5 дней;

— миллион книг, поставленных друг на друга, не выйдет даже за пределы атмосферы Земли;

— очередь, из миллиона букв можно составить одну, достаточно большую, книгу (например, полная Библия состоит из более чем 2,5 миллионов букв).

— миллион горошин поместится в большом мешке, который в принципе можно будет даже приподнять, если вы не боитесь надорваться;

— миллион песчинок запросто поместится в пригоршне;

— миллион бактерий будет едва различим невооруженному глазу.

— человеческий волос, увеличенный в миллион раз, будет диаметром около 100 метров.

— здание в миллион этажей (если бы такое можно было построить) поднялось бы в высоту на 2,5 тысячи километров, — в 4 с лишним раза выше, чем летает телескоп Хаббла и большинство искусственных спутников Земли.

Миллиард = 1 000 000 000 = 10⁹

Представить миллиард чего-то мы тоже можем:

— миллиард молекул, поставленных «плечом к плечу», займут около 30 сантиметров (вообще, молекулы сильно различаются по своим размерам и для примера мы взяли молекулу воды, состоящую, как известно, из двух атомов водорода и одного атома кислорода);

— головной мозг человека состоит из 100 миллиардов нейронов и столько же, но только людей, жило на нашей планете за всю ее историю.

— если разделить расстояние от Земли до Луны на миллиард, то получится примерно 40 сантиметров. А если на тот же миллиард разделить расстояние от Земли до Солнца, то получится уже 150 метров, а это большой такой небоскреб высотой почти в половину Эйфелевой башни. Сама Земля, уменьшенная в миллиард раз, станет размером с виноградину, — и, кстати, тогда она превратится в черную дыру;

— космические аппараты «Вояджер», запущенные в 1977 году, пролетели почти по 20 миллиардов километров каждый;

— миллиард секунд — это 31,7 года, целое поколение.

— если увеличить атом водорода в миллиард раз, то его диаметр составит целых 10 сантиметров, хотя его ядро даже при таком увеличении все равно не разглядишь. В этом масштабе мельчайшие вирусы будут гигантами размером в несколько десятков, а то и сотен метров. И даже молекула ДНК будет шириной в целых 3 метра.

Триллион = 1 000 000 000 000 = 10¹²

— общая масса воздуха, который вдыхают все люди на нашей планете за 1 год, составляет около 6 триллионов килограмм;

— в океанах нашей планеты обитает около триллиона рыб;

— триллион секунд, как вы наверняка уже догадались, это в тысячу раз дольше, чем миллиард, — то есть 31 с лишним тысяча лет;

— примерно столько времени назад вымерли неандертальцы. Но это секунды. А вот через триллион лет случится нечто гораздо более интересное — в галактиках прекратят образовываться новые звезды;

— триллион километров — такое расстояние свет в вакууме проходит чуть больше чем за месяц;

— 42 триллиона километров — это расстояние до ближайшей к нам звезды (Проксимы Центавра);

— если мы возьмем триллион бактерий (допустим, у нас как-то получится их собрать всех вместе), то они займут объем одного кубика сахара. Примерно столько бактерий содержится на теле человека. А число клеток в нем — несколько десятков триллионов;

— во всех когда-либо отпечатанных книгах за всю историю книгопечатания около 100 триллионов букв;

— горстку из триллиона атомов даже не увидеть невооруженным взглядом, вот насколько они малы. Например, электрон. Он будет размером с горошину. А вот кварки, увеличенные в триллион раз, все еще не будут видны.

Квадриллион = 1 000 000 000 000 000 = 10¹⁵

— в теле человека (не только на коже, как в предыдущем абзаце) обитает до 1 квадриллиона бактерий, и их общий вес составляет около 2 килограмм;

— на нашей планете живет примерно квадриллион муравьев (да, их гораздо больше, чем людей, — примерно в 100 тысяч раз);

— пролететь квадриллион километров (а это примерно 100 световых лет), то можно посетить несколько ближайших к Земле звезд и вернуться обратно;

— через 200 квадриллионов секунд Солнце перейдет в стадию красного гиганта;

— еще самые мощные современные компьютеры выдают несколько десятков квадриллионов операций в секунду (петафлопсов).

Квинтиллион = 1 000 000 000 000 000 000 = 10¹⁸

— квинтиллион километров — это примерный диаметр нашей галактики, которая называется Млечный Путь;

— до нашей соседки — галактики Андромеды — 25 квинтиллионов;

— квинтиллион секунд — это время в 2 раза большее, чем то, которое прошло от Большого Взрыва и до сегодняшнего момента;

— именно столько кубометров воды есть на земле;

— 25-30 квинтиллионов молекул содержится в 1 куб.см воздуха при нормальной температуре и давлении (в основном, это молекулы азота – 78% и кислорода – 21%);

— масса всей атмосферы Земли — около 5 квинтиллионов килограмм;

— число возможных комбинаций кубика Рубика — 43 квинтиллиона с лишним.

Секстиллион = 1 000 000 000 000 000 000 000 = 10²¹

— столько атомов содержится в небольшом шарике из алюминия, диаметром в пару миллиметров;

— вес гидросферы Земли – полтора секстиллиона килограмм, а Луны около 70 секстиллионов;

— количество песчинок на всех пляжах Земли — несколько секстиллионов, хотя это сильно зависит от того, как и что именно мы считаем;

— размер видимой ее части — примерно 130 секстиллионов километров. Разумеется, такие расстояния никто в километрах не меряет, а использует для этого куда более подходящие световые годы и парсеки.

Септиллион = 1 000 000 000 000 000 000 000 000 = 10²⁴

— 6 септиллионов килограмм весит наша Земля;

— количество звезд в обозримой Вселенной — септиллион или совсем немного меньше;

— знаменитое число Авогадро, обозначающее количество молекул в одном моле вещества, составляет почти септиллион (более точное значение: 6 на 10²³ степени);

— 10 септиллионов молекул воды поместится в одном стакане. А если выложить в ряд 50 септиллионов маковых зерен, то такая цепочка протянется до Туманности Андромеды.

Октиллион = 1 000 000 000 000 000 000 000 000 000 = 10²⁷

Октиллион горошин займут такой же объем как планета Земля. Еще это число интересно тем, что если взять 5-10 октиллионов атомов, то из них можно составить человеческое тело.

Казнер знаменит тем, что придумал слова «гугол» и «гуголплекс», а также известно решение Казнера для вакуумного пространства-времени (1922), к которому, согласно с гипотезой Белинского — Лифшица — Халатникова, приближается асимптотически любое космологическое решение около сингулярности.

Число Скьюза. Записывается как 10 в степени 10 в степени 10 в степени 963. Обозначает верхний предел для математической задачи.

3|||3 это 3 с высотой столба степени 3 равной расстоянию от Земли до Марса. Количество троек в степени равняется 7.000.000.000.000. И заметьте, это не само число, а его степень! Математики обозначили его G1. Всего 5 троек из этой башни полностью покрывают гуголплекс, а первые 10 сантиметров ставят в тупик все существующие на Земле компьютеры. Дальше пустота и неведение. Далее идёт число G2, где количество стрелок равняется G1. Далее идёт G3, где количество стрелок равняется G2 и так далее. Всего таких чисел 64. G64 это и есть число Грэма. Записать его где либо невозможно, поэтому записывают формулой: G=f^64(4), где f(n)=3|^n3. (значок «^» обозначает степень: 1.000.000=10^6). Подсчитывать это бессмысленно. Число Грэма не поместится в тех самых 10 в степени 500 вселенных, даже если пронумеровать каждую частицу! Но мы всё же кое что знаем о нём. Вот последние 10 цифр этого числа: 2464195387. Первые цифры не знает никто. Возможно, через тысячи или десятки тысяч лет человечество всё-таки сможет его высчитать и оно станет элементарным и банальным.

Источник

Число Грэма и взгляд в бесконечность

Вглядываться в бесконечность можно по-разному. Можно представлять себе всё увеличивающиеся астрономические числа и сопоставлять их с физическими явлениями. Можно всматриваться в выбранную точку фрактала Мандельброта, плавно увеличивая масштаб в 10 198 раз (можно и больше, но в угоду скорости страдает наглядность). Фрактал, сколь малую часть его не бери, остаётся самоподобным и сохраняет дробную структуру.

А можно представлять себе число Грэма так, как его представляет автор статьи «Число Грэма на пальцах». Число Грэма настолько велико, что даже если вы представите себе какое-то чудовищно большое астрономическое число, а потом возведёте его в столь же чудовищную степень, а потом повторите всё это чудовищное число раз — то вы даже не стронетесь с места на шкале того пути, что ведёт к числу Грэма. Чтобы сосчитать до числа Грэма, придётся научиться считать совсем иначе, нежели мы привыкли — представляя, что путь в бесконечность лежит через дописывание нулей к известным нам астрономическим числам. В этой системе счёта загибанию пальца на руке будет соответствовать не прибавление к числу единицы или миллиона, не дописывание нуля или сотен нулей разом, но шаг от сложения к умножению, от умножения к возведению в степень и дальше в невообразимые дали.

Сразу предупреждаю, что все эти упражнения небезыздержечны — не увлекайтесь, берегите своё душевное здоровье. Однако иногда полезно всмотреться в бесконечность, чтобы понять, где ты и что ты ей, как человек, можешь противопоставить.

Для меня в своё время взгляд бесконечность, подобный описанному «на пальцах» числу Грэма, дала функция Аккермана (которую приводят как пример сложной рекурсивной функции в теории алгоритмов). Она тесно связана со стрелочной записью Кнута, используемой в статье про число Грэма.

Если мы возьмём натуральное (т.е. неотрицательное целое) число и применим к нему операцию порядка, равного этому числу, то у нас получится примерно функция Аккермана (на самом деле, она определяется сложнее и от трёх или двух аргументов, но не суть).

Функция Аккермана растёт очень быстро, она растёт невыразимо быстро, она растёт быстрее чего угодно, что вы можете себе представить. Уже на пятом шаге она выходит за границы Вселенной. Но чтобы досчитать до числа Грэма за обозримое число шагов, даже её недостаточно. Нужно взять функцию Аккермана «второго порядка». Т.е. функцию Аккермана от функции Аккермана от функции Аккермана — и так Y раз. Получится эдакая «башенка» функций Аккермана. Вот такая «башенка» высотой в 64 этажа как раз до числа Грэма и досчитает.

Кажется, что осознание невыразимой величины этого числа может раздавить человека. Но не спешите с выводами. Автор упомянутой статьи, пытаясь оценить подступы к этому числу, сравнивает его элементы с числом частиц во Вселенной, сравнивает высоту «башенок» с расстоянием между планетами. Но вся эта кажущаяся с виду невыразимость сводится к числу «полтора». Ладно, пусть «два с половиной».

Поясню. Считать «бесконечность» (в кавычках — ибо любое число всё же конечно) нужно не тем, сколько песчинок она в себе содержит, а тем, сколько раз количество переходит в качество, сколько в ней нетривиальных идей. Посчитаем, сколько нетривиальных идей в числе Грэма. Функция Аккермана с её порядком арифметической операции как аргументом функции — идея раз. Применение функции Аккермана к самой себе — даже на полноценную идею не тянет, так, на половинку (а ведь можно представить и функцию Аккермана третьего порядка, чтобы ещё большее число получить — но тем отчётливее вырожденность идеи). Добавим ещё, собственно, описание задачи, в рамках которой появилось число Грэма (покраска в случайную комбинацию двух цветов диагоналей многомерных гиперкубов), чтобы иметь представление, где остановиться в нашем счёте — и получим две с половиной идеи.

Вроде, с одной стороны, почти необозримая бесконечность — а с другой стороны, тривиальность. Поставьте два зеркала друг напротив друга, встаньте между ними — и вы увидите бесконечное количество всё более тускнеющих отражений. Отражений бесконечное количество, но оригинал у них один — отражаетесь лишь вы сами.

Если в каком-то явлении вы замечаете, что с какого-то момента начинают повторяться лишь ухудшающиеся (в лучшем случае, такие же) копии того, что уже было раньше — то это дурная бесконечность, ложная. Движение по её шкале — лишь видимость жизни, но по сути это западня для вашего сознания.

Или вот был хороший оригинал — и сделали ему сиквел, приквел или ответвление сюжета. Чем наполнить? Известно чем — взять всё то же, что в оригинале, но в бОльших количествах и иначе скомбинированное. Была одна идея, стало полторы. Этих сиквелов можно теперь бесконечное число делать, зарабатывая деньги на тех, кому полюбился оригинал. И опять перед нами дурная бесконечность.

Вообще, возьми любой жанр — и большую часть его составят повторения, ухудшенные копии родоначальника жанра. Если вы чувствуете, что задыхаетесь в засилье этих похожих друг на друга отражений — плывите против течения, ищите источник отражений. Лишь так вы сможете в лабиринте дурной бесконечности отыскать истинный путь.

Источник

Число Грэма

Что такое Число Грэма

Число Грэма — это чрезвычайно большое конечное число и считается самым большим числом в мире, которое было использовано в математическом доказательстве (например, в теории Рамсея).

Используя стрелочные обозначения Кнута (стрелкой вверх), число Грэма G можно записать так:

Стрелочные обозначения Кнута используются в записи очень больших чисел.

3↑↑4 значит 3↑(3↑(3↑3)) или ;

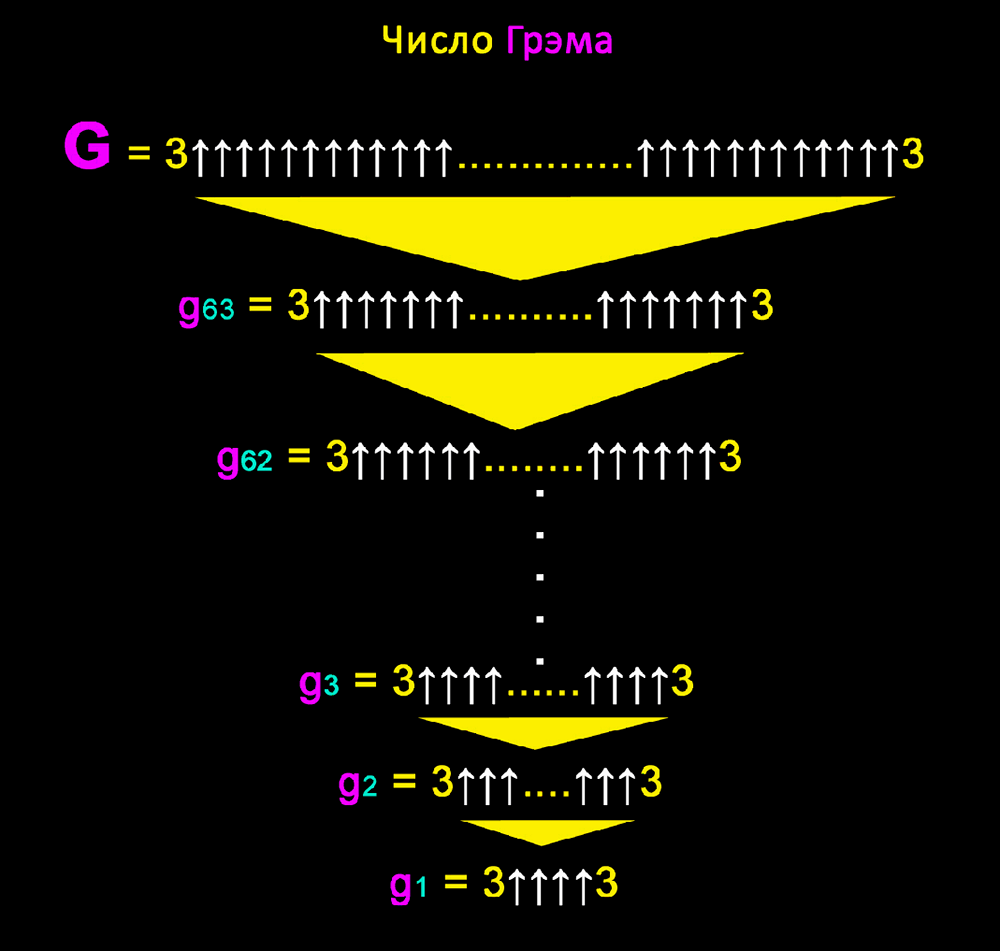
Что такое G64 и g1?

Ещё Число Грэма обозначают G64.

И g1 — это первый из 64 слоёв нужных для того, чтобы получить это число (на картинке сверху находятся остальные).

G1 можно немного упростить:

Количество стрелок g2 считается в g1. Далее процесс продолжается, до 64-го, последнего.

G = g64 — это последний слой, в нём g63 стрелок между тройками (как показано на картинке).

Однако только первый уровень G1 уже настолько велик, что считается, что его невозможно записать.

Что такое число гугол? И гуголплекс?

Гугол — это число равно 10¹ºº (десять в сотой степени) — это единица и сто нулей.

Гуголплекс — это 10^гугол (10 в степени «гугол») — это или .

Что такое число Райо?

Число Райо выглядит так: .

Считается, что эту функцию невозможно вычислить. Имеется в виду, что ни один современный компьютер не может её вычислить.

Узнайте также, что такое Экспонента и Логарифм.

Источник

Рональд Грэм, друг Бесконечности

Для своего времени (1977 год) и на протяжении многих лет это было самое больше число, использованное в математическом доказательстве.

И тем число Грэма ещё восхитительней, что для его понимания не нужно обладать специальным математическим образованием. Его может понять и испытать невероятный душевный трепет самый обычный человек с элементарными знаниями и хорошим творческим мышлением. Я это докажу.

Число Грэма настолько велико, что для него бессмысленны такие эпитеты как «огромное», «гигантское», «сверх-гигантское», «колоссальное», «чудовищное» и так далее. Любые определения превосходных категорий крайне убоги на фоне этого числа, поэтому мы сразу же успокоимся и для простоты назовём его просто: «Очень Большое число».

Рональд Грэм, друг Бесконечности

Число Грэма не имеет эквивалента в физическом мире, его невозможно отобразить предметно и даже вообразить в объеме чего-либо.

Это не количество песчинок в пустыне Сахара и всех остальных пустынь, не количество молекул воды в Мировом океане и не количество атомов во всей наблюдаемой Вселенной (≈10 80 ).

Как первое, так второе и третье, как бы это выразиться. ну скажем: ничтожное чуть более, чем ничто по сравнению с числом Грэма.

Более того, если представить, что существует столько других Вселенных, сколько атомов в нашей Вселенной, и в каждой из них тоже столько же атомов, сколько в нашей, и если все атомы этой Мультивселенной взять вместе – то это тоже будет чуть более, чем ничто по сравнению с числом Грэма.

Это выходит, что 10 80 нужно умножить на 10 80 – при умножении с одинаковыми основаниями показатели степени просто складываются, а основание остаётся неизменным: получится 10 160 – невидимая пыль в масштабе числа Грэма.

Можно в буквальном смысле всю жизнь сидеть и придумывать Мультивселенные мультивселенных, складывать и перемножать их атомы, но результатом будет все тот же: ничтожное чуть более, чем ничто по сравнению с числом Грэма.

Ну мы гугол даже рассматривать не будем в масштабе числа Грэма, эту станцию мы давно проехали. Но есть такое число как гуголплекс – десять в степени гугол.

Впечатляет, да? Цифру 10 нужно перемножить гугол раз. Гуголплекс нельзя записать в десятичной системе. Потому что придется написать цифру 1, а после неё гугол нулей. Понимаете? Не миллиард нулей написать после цифры 1, не триллион нулей, не дециллион, а гугол нулей!

Но у нас во Вселенной атомов меньше, чем гугол, как мы помним!

То есть если даже мы решим, что каждый атом – это отдельная цифра – «1» и «0», то их не хватит, чтобы записать гуголплекс! Да на чём писать-то?! На производство бумаги уже ничего не останется во Вселенной.

Поэтому гуголплекс можно записать только в виде степени, как показано выше.

Большое число гуголплекс? Оооочень большое!

А по сравнению с числом Грэма? Гм. ничтожное чуть более, чем ничто. Простите!

А гуголплекс в степени гуголплекс? Может уже близко к числу Грэма?

Ничтожное чуть более, чем ничто.

А гуголплекс в степени гуголплекс в степени гуголплекс в степени гуголплекс в степени гуголплекс – и так гуголплекс раз?! Ничтожное чуть более, чем ничто.

Я сильно понижу планку сравнений, потому что говорил о вещах абстрактных с крайне малым индексом воображения. А представьте себе обычную пшеничную муку. У каждого на кухне есть. Если набить пшеничной мукой под завязку нашу Вселенную, как мешок размером в 93 миллиарда световых лет, то будет слишком нелепо сравнивать количество крупинок муки с числом Грэма. Слишком нелепо! Число Грэма больше в невообразимое количество раз.

Я понимаю: рассуждения кажутся густо заливистыми и мошенническими – ну разве может такое быть, чтобы число атомов вселенных и мультивселенных, гуголплексы в степени гуголплексов – и всё это ничтожное?! – может, автор чеканулся?! – но когда вы позже поймёте число Грэма, сомнения развеются.

Но достаточно лирики в отношении предмета, перейдём к прозаическому его разъяснению. Конечно, я наговорил о нём предостаточно необъятно-возвышенного. Однако, с помощью особой записи, которую можно понять и без математического образования, вы осознаете если не масштаб числа Грэма (это невозможно), но хотя бы ухватите рассудком крупицу числа Грэма, затмевающую Вселенную.

Природа числа

Эту главу можно не читать, здесь просто объясняется, как Грэм пришёл к своему числу.

Важно понимать: число Грэма – это не просто выдуманная от нечего делать величина в математике, выдумать-то можно, что угодно. Оно не символическая абстракция, а прикладной инструмент. Число Грэма – доказательство в решении математической задачи.

Сама задача из области математики под названием комбинаторика. Тоже можно понять без специального образования. Я понял, поймете и вы.

Напишу предельно простым языком, не употребляя такие слова как «графы» и «подграфы»

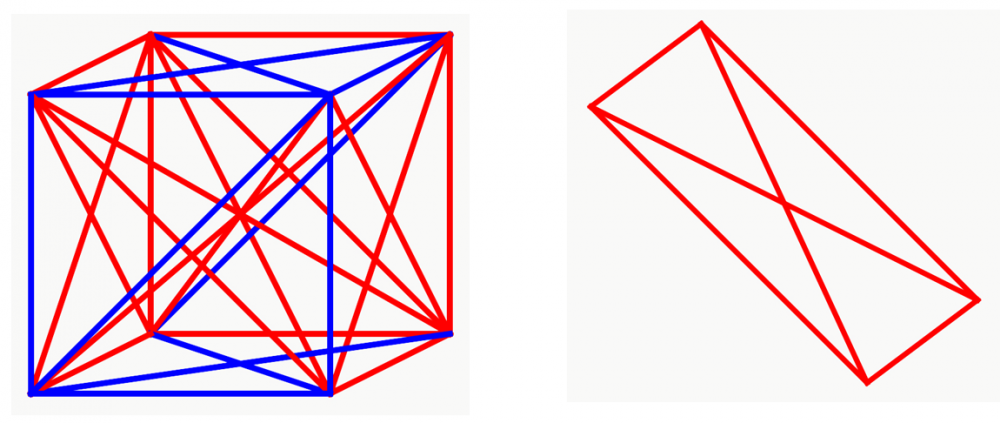
В общем так: у нас есть трехмерный куб. Все его вершины соединены линиями двух цветов – синего и красного. В произвольном порядке (но из каждой вершины должна исходить хотя бы одна линия другого цвета).

Можно распределить цвета так, что внутри куба получатся линии только одного цвета и лежащие в одной плоскости.

Как на рисунке справа.

Этакий красненький «андреевский» флаг или «почтовый» конвертик, как кому нравится. Но можно по-другому распределить цвета, и они не будут одного цвета в одной же плоскости – закрасить, например, одну линию «конвертика» синим.

А в четырехмерном кубе – тессеракте – можно тоже два варианта? Да, можно.

А в пятимерном? Да, можно.

В общем, математики дошли до шестимерного куба, и там всё также срабатывали оба варианта: можно и с одноцветным «конвертиком», и без него разукрасить.

На этом они остановились, потому что дело было в 70-х, и это был предел математических способностей того времени.

Но, конечно же, учёных продолжал безумно волновать вопрос: какой минимальной размерности должен быть куб, чтобы ИЗБЕЖАТЬ одноцветных линий в одной плоскости было НЕЛЬЗЯ?!

«Сколько-мерный» куб должен быть построен, когда как ни старайся, как ни комбинируй цветные линии, одноцветный «конвертик» обязательно будет наличествовать?!

Рональд Грэм предложил сокрушительный метод решения задачи: он доказал, что та самая размерность находится между цифрой 6 и неким Большим числом, которое он предложил. Может, уже семимерный куб даст неизбежный одноцветный «конвертик», а может, предпоследнее число перед Большим числом – где-то между ними – обязательно.

Проще говоря: Большое число – верхний предел размерности куба. Впоследствии это Большое число и назвали числом Грэма.

Кстати, в наше время нижняя граница поднялась повыше: до 13-мерного куба рассчитали математики – нет ещё обязательного одноцветного «конвертика»)))

Да, вы, конечно, можете поинтересоваться: «А почему они это делают, Грэм и другие?! Строят кубы, разрисовывают квадратики, ищут плоскости? Кому это надо вообще?!» Конечно, конечно. Но давайте так: две с половиной тысячи лет назад подобные вопросы задавали Пифагору и Евклиду их незатейливые современники, а вон оно как вышло. Не уподобляйтесь незатейливым современникам.

Приступим к осознанию числа Грэма.

Тройка

Нам понадобится цифра «3», которая должна быть возведена в Очень Большую Степень.

Но как я уже сказал, число Грэма нельзя записать не только в десятичной системе, но даже в виде степени это сделать невозможно. Однако, в семидесятых годах другой математик по имени Дональд Кнут разработал метод записи Больших чисел, который после назвали стрелочная нотация Кнута. Очень красиво звучит. Даже поэтически.

Я не буду разъяснять отдельно, что такое стрелочная нотация Кнута, чтобы не перегружать. Вы поймёте этот метод по ходу осознания числа Грэма. Также я не буду использовать особые термины (тетрация, пентация и гексация) с той же целью: не утяжелять восприятие. Как говорил Эйнштейн, нужно упрощать всё до предела, но не более того.

Итак, первый уровень:

«Одна стрелка»

Одна стрелка в нотации Кнута означает простое возведение цифры в какую-либо степень: 2↑4 = 2 4 = 16; 5↑3 = 5 3 = 125; 10↑5 = 10 5 = 100 000

Но у нас в основе цифра «3».

Всё просто! Пока всё очень просто.

Переходим на второй уровень.

«Две стрелки»

Тут тоже всё достаточно просто. При двух стрелках в нотации Кнута число справа указывает, в каком количество будет представлено число, которое находится слева, при горизонтальной развёртке записи «две стрелки» в запись «одна стрелка» – упрощаем.

Справа у нас цифра «3». И слева, так получилось, что она же.

Таким образом 3↑↑3 = 3↑3↑3 – и мы получаем последовательное возведение в степени троек.

Важно. Вычисление в стрелочной нотации Кнута производится справа-налево.

– это не 27↑3 = 27 3 = 19 683! – неправильно!

3↑↑3 = 3↑3↑3 = 3↑27 = 3 27 = 7 625 597 484 987!

Всего две стрелки в нотации Кнута и уже более 7 с половиной триллионов!

Но это ещё не всё. Нам придётся задержаться на уровне «две стрелки» и ввести такое понятие как «степенная башня», потому что дальше нам без него не обойтись.

Итак, возвращаемся к записи «две стрелки»: 3↑↑3

Схема построения степенной башни такая же, как при горизонтальной развёртке. Проще говоря, степенная башня – это вертикальная развёртка нотации Кнута.

Число справа указывает, в каком количестве будет представлено число, которое находится слева, при вертикальной развёртке:

– у нас получилась степенная башня!

Важно. Результат степенной башни вычисляется сверху-вниз!

То есть самое верхнее число обозначает степень, в которую нужно возвести число ниже, результат сам становится степенью, в которую нужно возвести число ниже. И так далее до самого нижнего числа.

3↑↑3 = 3 3 3 = 3 27 = 7 625 597 484 987

– как и при горизонтальной развёртке! Ну надо же – один результат )

Чтобы вы понимали: если бы справа была цифра «5», то развёртка выглядела бы так: 3↑↑5 = 3↑3↑3↑3↑3 – пять троек. И степенная башня состояла бы из пяти троек, и башню нужно было бы вычислять сверху вниз. Число уже огромное, позже придём к нему.

Думаю, всё понятно с двумя стрелками. Переходим на следующий уровень.

«Три стрелки»

Тут сложнее, но всё равно ещё доступно для быстрого понимания.

Применяем метод горизонтальной развёртки при трёх стрелках. Число справа указывает, в каком количестве будет представлено число слева, при горизонтальной развёртке записи «три стрелки» в запись «две стрелки».

Тогда 3↑↑↑3 = 3↑↑(3↑↑3) – три тройки, а между ними по две стрелки.

Берём развёртку в «две стрелки» и вычисляем правую часть, которая в скобках:

. (3↑↑3) – скобки и вставлены для того, чтобы показать очередность вычислений.

Это простая запись в «две стрелки», которую мы уже вычислили выше в виде горизонтальной развёртки в три тройки справа-налево и в виде степенной башни в три тройки же сверху-вниз, и у нас получилось 7 625 597 484 987.

Тогда подставляем это число вместо троек с двумя стрелками в скобках:

3↑↑↑3 = 3↑↑7 625 597 484 987

Как мы прекрасно помним, в записи «две стрелки» число справа указывает, в каком количестве будет представлено число, которое находится слева, при горизонтальной развёртке записи «две стрелки» в запись «одна стрелка».

3↑↑↑3 = 3↑↑7 625 597 484 987 = 3↑3↑3↑3. 3↑3↑3↑3

– и количество троек, между которыми будет «одна стрелка», будет равняться числу 7 625 597 484 987!

То есть цифры «3» нужно последовательно возвести в непомерно возрастающие степени, вычисляя справа-налево – когда результат вычисления справа становится степенью для тройки левее и так далее – 7 625 597 484 987 раз!

Или можно создать вертикальную развёртку и построить «степенную башню», при которой цифра «3» вытянется лестницей степеней в количестве 7 625 597 484 987 раз!

Если каждую тройку записывать в тетрадную клеточку, то высота такой башни составит примерно 38 миллионов километров – это расстояние до планеты Венеры.

Важно. Степенная башня высотой до Венеры – это не число с таким количеством цифр – да, оно тоже было бы гигантским! А это именно что степенная башня, которую нужно ещё вычислять, чтобы получить конечный результат в виде числа. И вычислять нужно, как мы помним, сверху-вниз!

Так вот если мы представим, что на Венере существует какая-то древняя могущественная цивилизация, и один из её представителей возьмётся для нас вычислить степенную башню в 7 625 597 484 987 троек, то он будет спускаться по ней как по лестнице.

Первая ступенька – 3.

Вторая ступенька – 27.

Третья ступенька – 7 625 597 484 987

Четвёртая ступенька – 3 7 625 597 484 987 – понятия не имею, сколько это будет, вычислить уже нельзя подручными мощностями. Только супер-компьютер справится.

Пятая ступенька – 3 3 7 625 597 484 987 – тройка в степени тройки, которая сама в степени более 7 с половиной триллионов!

Это число, которое уже нельзя вычислить ни на одном супер-компьютере.

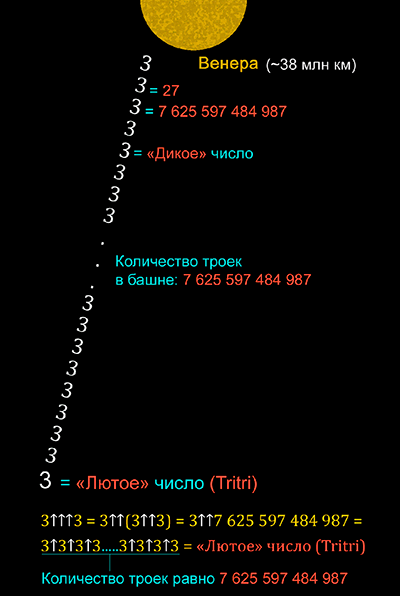
Гуголплекс побледнел перед ним и рассыпался. Это какое-то «Дикое» число! И оно всего лишь на пятой ступеньке вниз! А их там. ещё более

7 с половиной триллионов ступенек-троек! И каждая нижняя возводится в степень числа, которое получилось при вычислении верхней предыдущей.

Это – чудовищно-взрывная прогрессия.

Мы понятия не имеем в какую степень должна быть возведена самая нижняя ступенька-тройка, равно как понятия не имеем, каков будет результат – что это будет за конечное число в вычислении степенной башни?!

Но допустим, представитель древней могущественной венерианской цивилизации справился с вычислением. И не имея возможности назвать его нам, потому что в человечьем языке нет таких слов и масштабов в сознании, венерианец ограничился образным определением и назвал его «Лютое» число.

В земном научном мире у него, правда, есть название – «Tritri» («Тритри»).

Итак: 3↑↑↑3 = 3↑↑(3↑↑3) = 3↑↑7 625 597 484 987 = Лютое число (Tritri)

И для большей наглядности я нарисовал инфографику.

Переходим на следующий уровень.

«Четыре стрелки»

Я бы хотел написать «а вот это уже сложно», но если вы поняли предыдущие вычисления, то нет! Не сложно, хоть и массивней.

Применяем метод горизонтальной развёртки по прежнему алгоритму: в записи «четыре стрелки» число справа указывает, в каком количестве число слева будет представлено при переводе в запись «три стрелки»:

Мы её вычислили выше. И у нас получилось Лютое число или Тритри.

Подставляем его в горизонтальную развёртку:

Смотрим опять на нотацию «три стрелки»:.

Мы помним, что при записи «три стрелки» число справа указывает, в каком количестве число слева будет представлено в горизонтальной развёртке при переводе в запись «две стрелки». А справа у нас – Лютое-Тритри число.

. 3↑↑↑Лютое-Тритри = 3↑↑(3↑↑(3↑↑(3. (3↑↑(3↑↑(3↑↑3)) – таким образом мы видим, что при переводе записи «три стрелки» в запись «две стрелки» количество троек, между которыми «две стрелки», будет равняться. Лютому-Тритри числу!

Значит, в целом получается, что:

3↑↑↑↑3 = 3↑↑↑(3↑↑↑3) = 3↑↑↑Лютое-Тритри = 3↑↑(3↑↑(3↑↑(3. (3↑↑(3↑↑(3↑↑3)) – таким образом выходит, что в нашем случае нотация «четыре стрелки» разворачивается в конечном итоге в нотацию «две стрелки», где количество троек будет равняться Лютому-Трири числу. Скобки поставлены для того, чтобы обозначить первоочерёдность вычисления – справа-налево.

Значит, можем исключить из записи нотацию «три стрелки» – она своё отработала, и упростить нотацию «четыре стрелки».

– где количество троек в нотации «две стрелки» – Лютое-Тритри. Скобки я тоже убрал, чтобы не смущали.

Нет никакого смысла пытаться представить длину этой цепочки.

Идём дальше и метод горизонтальной развёртки дополняем вертикальными развёртками – степенными башнями.

Мы помним, что запись «две стрелки» означает, что число справа указывает, в каком количестве будет представлено число слева при вертикальной развёртке, то есть при построении степенной башни.

И у нас тут Лютое-Тритри число троек с «двумя стрелками», которые взаимосвязаны в цепочке горизонтальной развёртки.

Начинаем строить в горизонтальной развёртке степенные башни и вычислять сверху-вниз, двигаясь справа-налево.

Тогда строим башни и вычисляем, начиная с крайних справа троек:

= 3↑↑3↑↑3↑↑3. 3↑↑3↑↑3↑↑7 625 597 484 987

Получается, что тройка левее должна вырасти в степенную башню, состоящую аж из 7 625 597 484 987 троек – до Венеры, помните! Я её нарисовать уже не могу тут)

И когда мы вычислим эту башню сверху-вниз, то получим наше старое доброе Лютое-Тритри число!

А следующая тройка левее должна, соответственно, вырасти в степенную башню, состоящую и Лютого-Тритри числа троек! И когда мы вычислим эту степенную башню сверху-вниз, то получим число, назовём его Лютое-1.

А следующая тройка левее должна вырасти в степенную башню, состоящую из Лютого-1 числа троек. И так далее! – мы должны двигаться левее-левее-левее. – сверхчудовищная, сверхвзрывная прогрессия от башни к башне.

И всего троек-башен у нас, как мы помним, в цепочке горизонтальной развёртки Лютое-Тритри число (учитывая, что самая права тройка – тоже башня, маленькая такая, из одной цифры).

Помним: каждая башня левее состоит из количества троек, полученного при вычислении числа предыдущей башни, которая справа.

Таким образом, когда последняя тройка слева вырастит в башню, состоящую из невообразимого числа троек, полученного при вычислении предпоследней башни; и когда мы вычислим последнюю башню, то мы получим совершенно «Жуткое» число. Или как оно называется по-научному – g1.

Для простоты понимания смотрите инфографику.

Я, конечно, тут разошёлся малость – «вычислим Лютое число, вычислим Лютое-1 число, вычислим число g1!» – смешно!

Если помните, то Лютое-Тритри нам вычислил венерианец. Сами мы не вычислим ничего. Это абсолютно невозможно.

Жуткое-g1 число – запредельно, оно за гранью всех мыслимых и немыслимых Вселенных и Мультивселенных.

И это уже число Грэма? Гм. Честно сказать: не совсем )

Давайте снова маленькое лирическое отступление.

Знаете, есть такая наука палеонтология – изучение древней жизни на Земле. В нашем случае проще говоря – динозавров. Известно, что многие из них были большими и очень большими животными. Но целиком окаменелый скелет обнаружить очень трудно. Палеонтологи чаще всего находят фрагменты, например, уцелевший позвонок аргентинозавра или амфицелия, например. И учитывая размер позвонка – 1,8 – 2,5 метров высоту, прикидывают габариты животного в целом – получается внушительно: 40 – 50 метров в длину.

Так вот Жуткое-g1 число – это фрагмент числа Грэма, но! – с небольшими поправками. Всё-таки позвонок динозавра – довольно крупный фрагмент динозавра.

А g1 – как бы это сказать, не очень крупный фрагмент числа Грэма.

Это не только не позвонок, но и даже не клетка числа Грэма. А уж если быть совсем точным – это даже не атом числа Грэма.

g1 – запредельное гигантское, невообразимое число – это какая-то субатомная, запредельно маленькая частица числа Грэма, неразличимая в масштабе его тела целиком никоим образом. Никоим!

Проследим ещё раз наш путь:

3↑↑3 = 7 625 597 484 987

3↑↑↑3 = Лютое-Тритри число

3↑↑↑↑3 = Жуткое-g1 число

Понимаете, что всего четыре шага – от одной стрелки до четвёртой включительно – и мы получили феноменальную прогрессию от числа 27 до Жуткого-g1 числа.

Всего четыре стрелки!

Но вслед за g1 идёт g2 число.

Что оно из себя представляет?

Да это очень просто:

g2 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g1. Это мучительно больно!

Понимаете, да?! «Четыре стрелки» катастрофическим образом разнесли наше представление о размерности и масштабах в виде необъятного числа g1.

И следующий уровень – это «g1 стрелок», которые нужно поместить между двумя тройками.

В результате мы получим число g2. То есть никогда мы ничего не получим, это я просто так говорю – образно, поэтически)))

А после g2 идёт число g3. Что это такое? Тоже просто:

g3 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g2.

g4 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g3.

g5 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g4.

g63 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g62.

И наконец 64-й слой:

g64 = 3↑↑↑↑↑↑. ↑↑↑↑↑↑↑3 – где количество стрелок равно. g63.

и привет Бесконечности! )

А есть ли число больше, чем число Грэма, которое также применялось в математическом доказательстве?

И называется это число TREE(3) – ДЕРЕВО(3)

И о нём как-нибудь в другой раз )

Конечно же, число Грэма – вымышленный персонаж физико-математического мира. Но так получилось, что многие персонажи этого мира – хоть вымышленные, хоть нет – производят несоизмеримо большее драматическое впечатление, чем любые вымышленные персонажи из лирико-художественного мира. Просто мало кто об этом задумывается.

Источник