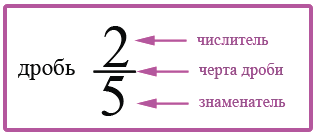числитель и знаменатель что это такое

Доли. Обыкновенные дроби

Нам известно, что при подсчете чего-либо мы используем натуральные числа, но часто приходится что-то целое делить на части. Например, нам дан апельсин:

Допустим, нам надо разделить апельсин на 6 равных частей:

В этом случае каждую часть называют долей. То есть целый апельсин разделили на 6 частей, поэтому мы можем сказать, что апельсин это 1 целая, и 6 долей апельсина тоже составляет 1 целую:

Название долей зависит от числа частей. Каждая доля в нашем случае будет называться «одной шестой долей апельсина» или, короче, «одной шестой апельсина«. Если апельсин поделить на 8 частей, то мы получим восьмые доли. При этом, чем на большее число частей делят целое, тем меньше доля.

Например, рассмотрим брусок:

Разделим его на 5 частей:

То есть мы получим пятые доли бруска. Закрасим две части красным:

Теперь закрасим три части бруска:

Мы закрасили три пятые доли. Дробь, обозначающая эти доли, записывается так: .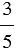

Теперь закрасим желтым цветом пять частей бруска:

Мы закрасили пять пятых долей, то есть мы закрасили весь брусок. Дробь, обозначающая эти доли, записывается так: .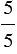

Рассмотрим рисунок ниже:

Определения

Правильная дробь – это дробь, числитель которой меньше знаменателя.

Неправильная дробь – это дробь, у которой числитель больше знаменателя или равен ему.

Поделись с друзьями в социальных сетях:

Источник

Числитель и знаменатель

Числитель дроби — это число, стоящее в записи обыкновенной дроби над дробной чертой, то есть сверху. Числитель показывает количество долей.

Знаменатель дроби — это число, стоящее в записи дроби под дробной чертой, то есть снизу. Знаменатель показывает, какие это доли и на сколько равных частей разделена единица.

Дробная черта — это горизонтальная черта в записи дроби, которая отделяет числитель и знаменатель друг от друга.

Вместе, числитель и знаменатель дроби, называются членами дроби.

Условились считать, что дробная черта означает деление верхнего числа на нижнее, поэтому:

Любую операцию деления можно записать в виде дроби. И наоборот, любую дробь можно записать в виде операции деления.

Как читать запись обыкновенных дробей

По этому правилу читаются все обыкновенные дроби.

Пример 1. Прочитайте дробь , назовите числитель и знаменатель.

Пример 2. Прочитайте дробь .

Пример 3. Прочитайте дробь .

Источник

Доли, обыкновенные дроби: определения, обозначения, примеры, действия с дробями

Рассмотрение данной темы мы начнем с изучения понятия доли в целом, которое даст нам более полное понимание смысла обыкновенной дроби. Дадим основные термины и их определение, изучим тему в геометрическом толковании, т.е. на координатной прямой, а также определим список основных действий с дробями.

Доли целого

Представим некий предмет, состоящий из нескольких, совершенно равных частей. Например, это может быть апельсин, состоящий из нескольких одинаковых долек.

Доля целого или доля – это каждая из равных частей, составляющих целый предмет.

Очевидно, что доли могут быть разные. Чтобы наглядно пояснить это утверждение, представим два яблока, одно из которых разрезано на две равные части, а второе – на четыре. Ясно, что размеры получившихся долей у разных яблок будут различаться.

Доли имеют свои названия, которые зависят от количества долей, составляющих целый предмет. Если предмет имеет две доли, то каждая из них будет определяться как одна вторая доля этого предмета; когда предмет состоит из трех долей, то каждая из них – одна третья и так далее.

Половина – одна вторая доля предмета.

Треть – одна третья доля предмета.

Четверть – одна четвертая доля предмета.

Понятие доли естественно расширяется с предметов на величины. Так, можно использовать для измерения небольших предметов доли метра (треть или одна сотая), как одной из единиц измерения длины. Аналогичным образом можно применить доли других величин.

Обыкновенные дроби, определение и примеры

Обыкновенные дробиприменяются для описания количества долей. Рассмотрим простой пример, который приблизит нас к определению обыкновенной дроби.

Числитель и знаменатель

Т.е. числитель – число, расположенное сверху над чертой обыкновенной дроби (или слева от наклонной черты), а знаменатель – число, расположенное под чертой (справа от наклонной черты).

Какой же смысл несут в себе числитель и знаменатель? Знаменатель обыкновенной дроби указывает на то, из скольких долей состоит один предмет, а числитель дает нам информацию о том, каково рассматриваемое количество таких долей. К примеру, обыкновенная дробь 7 54 указывает нам на то, что некий предмет состоит из 54 долей, и для рассмотрения мы взяли 7 таких долей.

Натуральное число как дробь со знаменателем 1

Черта дроби как знак деления

Использованное выше представление данного предмета как n долей является не чем иным, как делением на n равных частей. Когда предмет разделен на n частей, мы имеем возможность разделить его поровну между n людьми – каждый получит свою долю.

При помощи обыкновенной дроби мы можем записать итог деления двух натуральных чисел. К примеру, деление 7 яблок на 10 человек запишем как 7 10 : каждому человеку достанется семь десятых долей.

Равные и неравные обыкновенные дроби

Результатом сравнения обыкновенных дробей может быть: равны или неравны.

В случае, когда выясняется, что дроби не являются равными, обычно необходимо также узнать, какая из данных дробей меньше, а какая – больше. Чтобы дать ответ на эти вопросы, обыкновенные дроби сравнивают, приводя их к общему знаменателю и затем сравнив числители.

Дробные числа

Дроби на координатном луче

Все дробные числа, как и любое другое число, имеют свое уникальное месторасположение на координатном луче: существует однозначное соответствие между дробями и точками координатного луча.

Здесь работает тот же принцип, что и с целыми числами: на горизонтальном, направленном вправо координатном луче точка, которой соответствует большая дробь, разместится правее точки, которой соответствует меньшая дробь. И наоборот: точка, координата которой – меньшая дробь, будет располагаться левее точки, которой соответствует бОльшая координата.

Правильные и неправильные дроби, определения, примеры

В основе разделения дробей на правильные и неправильные лежит сравнение числителя и знаменателя в пределах одной дроби.

Источник

Дроби обыкновенные правильные и неправильные, смешанные и составные.

Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дроби являются частью поля рациональных чисел. По способу записи дроби делятся на 2 формата: обыкновенные вида и десятичные.

Числитель дроби — число, показывающее количество взятых долей (находится в верхней части дроби – над чертой). Знаменатель дроби — число, показывающее, на сколько долей разделена единица (находится под чертой – в нижней части). Обыкновенные дроби, в свою очередь делятся на: правильные и неправильные, смешанные и составные. Обыкновенные дроби тесно связаны с единицами измерения. 1 метр содержит в себе 100 см. Что означает, что 1 м разделён на 100 равных долей. Таким образом, 1 см = 1/100 м (один сантиметр равен одной сотой метра).

или 3/5 (три пятых), здесь 3 — числитель, 5 — знаменатель. Если числитель меньше знаменателя, то дробь меньше единицы и называется правильной:

Если числитель равен знаменателю, дробь равна единице. Если числитель больше знаменателя, дробь больше единицы. В обоих последних случаях дробь называется неправильной:

Чтобы выделить наибольшее целое число, содержащееся в неправильной дроби, нужно разделить числитель на знаменатель. Если деление выполняется без остатка, то взятая неправильная дробь равна частному:

Если деление выполняется с остатком, то (неполное) частное дает искомое целое число, остаток же становится числителем дробной части; знаменатель дробной части остается прежним.

Число, содержащее целую и дробную части, называется смешанным. Дробная часть смешанного числа может быть и неправильной дробью. Тогда можно из дробной части выделить наибольшее целое число и представить смешанное число в таком виде, чтобы дробная часть стала правильной дробью (или вовсе исчезла).

К подобному виду обычно и приводят смешанные дроби.

Составные дроби.

Многоэтажной, или составной дробью является дробь, которая содержит в себе несколько горизонтальных (либо реже — наклонных) черт:

либо либо .

Источник

Обыкновенные дроби. Числитель, знаменатель. Доли в дробях.

Обыкновенные дроби. Понятие дроби. Доли в дробях.

Дроби мы постоянно используем в жизни. Например, когда едим торт с друзьями. Торт можно разделить на 8 равных частей или на 8 долей. Доля – это равная часть от чего-то целого. Четыре друга съели по кусочку торта. Четыре взяли из восьми кусочков можно записать математически в виде обыкновенной дроби \(\frac<4><8>\), читается дробь “четыре восьмых” или “четыре деленное на восемь”. Обыкновенную дробь еще называют простой дробью.

Дробная черта заменяет деление:
\(4 \div 8 = \frac<4><8>\)
Это мы записали доли в дробях. В буквенном виде будет так:
\(\bf m \div n = \frac\)

4 – числитель или делимое, находится вверху над дробной чертой и показывает сколько частей или долей из общего было взято.
8 – знаменатель или делитель, находится внизу под дробной чертой и показывает общее количество частей или долей.

Если мы приглядимся внимательно, то увидим, что друзья съели половину торта или одну часть из двух. Запишем в виде обыкновенной дроби \(\frac<1><2>\), читается “одна вторая”.

Рассмотрим еще пример:
Имеется квадрат. Квадрат разделили на 5 равных частей. Две части закрасили. Запишите дробь для закрашенных частей? Запишите дробь для не закрашенных частей?

Две части закрасили, а всего частей пять, поэтому дробь будет иметь вид \(\frac<2><5>\), читается дробь “две пятых”.
Три части не закрасили, всего частей пять, поэтому дробь запишем так \(\frac<3><5>\), читается дробь “три пятых”.

Разделим квадрат на более мелкие квадраты и запишем дроби, для закрашенных и не закрашенных частей.

Закрашенных 4 части, а всего 25 частей. Получаем дробь \(\frac<4><25>\), читается дробь “четыре двадцать пятых”.
Не закрашенных 21 частей, а всего 25 частей. Получаем дробь \(\frac<21><25>\), читается дробь “двадцать один двадцать пятых”.

Любое натуральное число можно представить в виде дроби. Например:

Любое число делиться на единицу, поэтому это число можно представить в виде дроби.

Вопросы по теме “обыкновенные дроби”:
Что такое доля?
Ответ: доля – это равная часть от чего-то целого.

Что показывает знаменатель?
Ответ: знаменатель показывает на сколько всего частей или долей поделено.

Что показывает числитель?
Ответ: числитель показывает сколько частей или долей было взято.

Дорога составляла 100м. Миша прошел 31м. Запишите дробью выражение сколько прошел Миша?
Ответ:\(\frac<31><100>\)

Что такое обыкновенная дробь?
Ответ: обыкновенная дробь – это отношение числителя к знаменателю, где числитель меньше знаменателя. Пример, обыкновенных дробей \(\frac<1><4>, \frac<3><7>, \frac<5><13>, \frac<9><11>…\)

Как перевести натуральное число в обыкновенную дробь?
Ответ: любое число можно записать в виде дроби, например, \(5 = \frac<5><1>\)

Задача №1:
Купили 2кг 700г дыни. Мише отрезали \(\frac<2><9>\) дыни. Чему равна масса отрезанного кусочка? Сколько граммов дыни осталось?

Решение:
Переведем килограммы в граммы.
2кг = 2000г
2000г + 700г = 2700г всего весит дыня.

Мише отрезали \(\frac<2><9>\) дыни. В знаменателе стоит число 9, значит на 9 частей разделили дыню.
2700 : 9 =300г масса одного кусочка.
В числители стоит число 2, значит надо Мише дать два кусочка.
300 + 300 = 600г или 300 ⋅ 2 = 600г столько дыни съел Миша.

Чтобы найти какая масса дыни осталась нужно вычесть от общей массы дыни съеденную массу.
2700 — 600 = 2100г осталось дыни.

Источник