бухгольц в шахматах что это
Бухгольц в шахматах что это
В шахматах дополнительные показатели очень неоднозначны, нуждаются в пояснении, да ещё их очень много и они разные. На одних турнирах применяются одни, на других другие.
Итак, два или более участника в турнире по швейцарской системе, набрали одинаковое количество очков. Кто из них занял какое место?
1. Коэффициент Бухгольца.
В турнире по швейцарской системе, каждый конкретный участник играет не со всеми остальными, а с определённым количеством участников (у которых в каждом из туров было приблизительно столько же очков). Эти наши соперники, закончив турнир, набрали очки. Идея коэффициента Бухгольца достаточно проста. Складываем очки всех соперников каждого из разделивших места участников, и тот, у которого соперники набрали больше очков, становится победителем нашего турнира. Ему, ведь, было тяжелее всех! Он играл с более сильными! Если Вы поняли, о чём речь, то этот дополнительный показатель должен Вам понравится! Его справедливость более менее ясна. И он бы всегда и всеми применялся, если бы не одно очень неожиданное НО!
Представьте себе, что в одном из первых туров, Вы сыграли партию с неким N. Тут даже не очень важно каким был результат (выиграли, проиграли или вничью). И вот этот N, скажем после третьего тура, взял да и бросил турнир (заболел, расхотелось играть. ). Больше он в этом турнире очков не получит, и потянет весь ваш коэффициент Бухгольца вниз! А это уже несправедливо! Вы же не виноваты, что он бросил турнир! А при дележе, Ваши шансы получить более худшее место заметно возрастают по сравнению с теми, кто с этим N не играл.
Эту проблему попытались решить математически. Смысл был прост. Участник выбыл после третьего тура. Смотрим, сколько очков набрали в турнире все участники, кто после третьего тура имел столько же очков, сколько и этот N, берём среднее, и считаем, что N набрал бы именно столько очков, сколько это среднее. Получается своего рода виртуальный Бухгольц.
Другим вариантом решения проблемы выбывшего участника, явился так называемый усечённый Бухгольц. При его вычислении, отбрасываются очки соперника, показавшего самый плохой результат. Это называется Бухгольц, усечённый снизу.
А ещё некоторые программы для проведения жеребьёвки просто не считают ни усечённый Бухгольц, ни виртуальный! Поэтому коэффициент Бухгольца ни простой, ни усечённый, могут не являться приоритетными показателями на некоторых соревнованиях.
2. Коэффициент Бергера.
Этот показатель является своего рода уточнённым Бухгольцем. Попросту говоря, если при подсчёте коэффициента Бухгольца учитываются все очки Ваших соперников, то в коэффициенте Бергера складываются очки набранные соперниками у которых Вы выиграли, очки набранные соперниками с которыми Вы сыграли вничью делятся пополам, а очки соперников которым Вы проиграли просто не учитываются.
Коэффициент Бергера является основным показателем при проведение круговых турниров, так как там Бухгольц просто не работает. Ведь в круговом турнире все участники обязательно переиграют друг с другом и если двое наберут одинаковое количество очков, то их соперники в сумме наберут столько же и коэффициент Бухгольца всегда будет одинаков. Правда, в турнирах по швейцарской системе, Бергер, хотя и считается программами, но в качестве дополнительного показателя практически никогда не используется.
Прогресс, или нарастающий итог это сумма очков участника, набранная им после каждого тура.
Пример. Участник N сыграл в турнире по швейцарской системе в 7 туров следующим образом: 1, 0, 0.5, 1, 1, 0, 1, Тогда, после первого тура у него было 1 очко, после второго 1 очко, после третьего 1,5, после четвёртого 2,5, после пятого 3,5, после шестого 3,5, после седьмого 4,5. Складываем все эти числа 1+1+1,5+2,5+3,5+3,5+4,5=17,5. Это и есть прогресс.
Смысл этого коэффициента в том, что чем лучше участник стартовал, тем он будет больше. А те, кто стартовал лучше, как правило, получают более сильных соперников.
Есть ещё и другие дополнительные показатели. Например, средний рейтинг соперников, количество партий сыгранных чёрным цветом, а можно что-нибудь придумать самому. Например (в детских соревнованиях), отдавать при дележе более высокое место младшему по возрасту (по дате рождения). Правда, есть маленькая вероятность, что может случиться так, что придётся делать запросы в роддома, на предмет точного времени рождения если ненароком участники родились в один день. А в турнирах для ветеранов, можно тем же способом отдавать предпочтения более пожилому шахматисту.
Подведём итоги. ОПТИМАЛЬНОГО КОЭФФИЦИЕНТА НЕ СУЩЕСТВУЕТ! Каждый имеет свои плюсы и минусы. И, если Вы хотите, чтобы эти математические хитросплетения не лишали Вас призовых мест, то надо просто выигрывать все партии. Тогда, никакой, даже самый заумный коэффициент не поможет Вашим соперникам.
Коэффициенты Бухгольца и Бергера
 Коэффициент Бергера
Коэффициент Бергера
Коэффициент Бергера – способ определения мест (дополнительный коэффициент) в соревнованиях среди участников, набравших равное количество очков в основном турнирном зачете. Применяется в играх, где за победу, ничью и поражение присуждается определенное постоянное число очков (например, 1, 0.5 и 0 – в шахматах, шашках, Го, рэндзю и т.д.).
Первым такую систему подсчета очков при распределении мест предложил чехословацкий шахматный мастер Оскар Гелбфус (Oskar Gelbfuhs) в августе 1873 года.
Коэффициент Бергера был первоначально разработан для круговых шахматных турниров, где каждый участник играет с каждым. Позже этот метод стали применять и для соревнований по другим играм, например, Го.
На практике коэффициент Бергера впервые применили Уильям Зонненборн (William Sonneborn) и Иоганн Бергер (Johann Berger) на турнире в Ливерпуле в 1882 году. В 1886 году распределение мест по коэффициенту Бергера было введено в регулярную практику.
Коэффициент Бергера определенного участника складывается из суммы всех очков противников, у которых данный участник выиграл, плюс половина суммы очков противников, с которыми данный участник сыграл вничью. Идея, на которой базируется коэффициент: из двух участников, равных по числу очков, сильнее тот, кто выиграл у более сильных противников, то есть у тех, кто набрал больше очков. Поэтому участнику, имеющему больший коэффициент Бергера, присуждается более высокое итоговое место в турнире.
Коэффициент Бергера придуман для круговых турниров, но может, при необходимости, применяться и в других схемах розыгрыша с равным числом партий, например, в турнирах по швейцарской системе (хотя традиционно там применяется коэффициент Бухгольца).
Коэффициент Бухгольца
Коэффициент Бухгольца – способ определения мест (дополнительный коэффициент) в турнирах среди участников, набравших равное количество очков. Так же, как и коэффициент Бергера, применяется в играх, где за победу, ничью и поражение присуждается постоянное число очков. Однако, в отличие от коэффициента Бергера, который чаще всего применяется в круговых турнирах, коэффициент Бухгольца используется в турнирах, проводимых по швейцарской системе. В круговых турнирах система Бухгольца не применяется, т.к. в случае равенства очков в основном зачете, соперники будут иметь и равные коэффициенты.
Способ определения мест в соревнованиях среди участников, набравших равное количество очков, по коэффициенту Бухгольца был предложен в 1932 году и был назван по имени его изобретателя – шахматиста Бруно Бухгольца (Bruno Buchholz).
Коэффициент Бухгольца определенного участника складывается из суммы всех очков соперников, с которыми данный участник играл, независимо от результата встреч между ними. Идея заключается в том, что Участнику, игравшему с более сильными соперниками (соперниками, набравшими в сумме больше очков), присуждается более высокое итоговое место.
Усеченный коэффициент Бухгольца
Если у двух или более участников оказываются равными и количество набранных очков, и коэффициенты Бухгольца, то из коэффициента Бухгольца каждого участника вычитают результат соперника с меньшим количеством очков. Если после такого вычитания коэффициенты Бухгольца (без результата соперника с меньшим количеством очков) остаются равными, то процедура повторяется, то есть вычитают результат следующего слабейшего соперника и т.д.
Коэффициенты Бухгольца и Бергера изначально применялись только в турнирах по шахматам, однако, затем широко распространились и на другие игры, в которых результат строго фиксирован по набранным очкам (победа, поражение или ничья).
Примечание. К вопросу о расчете коэффициентов при пропуске тура и неявке соперника.
Как правило, используется следующий подход.
Все несыгранные партии (пропуск тура, неявка или нехватка соперника, «плюс») в целях подсчета коэффициентов условно считаются ничейными:
Коэффициент Бухгольца
Определение и применение [ ]
В турнирах часто случается так, что два или несколько участников набирают одинаковое количество очков. В этих случаях применяют коэффициент Бухгольца. Участнику, имеющему больший коэффициент Бухгольца, присуждается более высокое итоговое место в турнире. Коэффициент Бухгольца определённого участника складывается из суммы всех очков соперников, с которыми данный участник играл, независимо от результата встреч между ними. Идея заключается в том, что участнику, игравшему с более сильными соперниками (соперниками, набравшими в сумме больше очков), присуждается более высокое итоговое место. Все несыгранные партии (+/-) условно считаются ничейными.
Если у двух или более участников оказываются равными и количество набранных очков, и коэффициенты Бухгольца, то из коэффициента Бухгольца каждого участника вычитают результат соперника с меньшим количеством очков. Если после такого вычитания коэффициенты Бухгольца (без результата соперника с меньшим количеством очков) остаются равными, то процедура повторяется: вычитается результат следующего слабейшего соперника, и т.д. Иногда такой коэффициент называют усечённым коэффициентом Бухгольца.
В круговых турнирах система распределения мест по коэффициентам Бухгольца неприменима, так как в них каждый играет с каждым, и поэтому участники, набравшие одинаковое количество очков, имеют также равные коэффициенты Бухгольца. В круговых турнирах применяют коэффициенты Бергера.
История [ ]
Коэффициенты Бухгольца и Бергера
Коэффициенты Бухгольца и Бергера

Первым такую систему подсчета очков при распределении мест предложил чехословацкий шахматный мастер Оскар Гелбфус (Oskar Gelbfuhs) в августе 1873 года.
Коэффициент Бергера был первоначально разработан для круговыхшахматных турниров, где каждый участник играет с каждым. Позже этот метод стали применять и для соревнований по другим играм, например, Го.
На практике коэффициент Бергера впервые применили Уильям Зонненборн (William Sonneborn) и Иоганн Бергер (Johann Berger) на турнире в Ливерпуле в 1882 году. В 1886 году распределение мест по коэффициенту Бергера было введено в регулярную практику.
Коэффициент Бергера определенного участника складывается из суммы всех очков противников, у которых данный участник выиграл, плюс половина суммы очков противников, с которыми данный участник сыграл вничью. Идея, на которой базируется коэффициент: из двух участников, равных по числу очков, сильнее тот, кто выиграл у более сильных противников, то есть у тех, кто набрал больше очков. Поэтому участнику, имеющему больший коэффициент Бергера, присуждается более высокое итоговое место в турнире.
Коэффициент Бергера придуман для круговых турниров, но может, при необходимости, применяться и в других схемах розыгрыша с равным числом партий, например, в турнирах по швейцарской системе (хотя традиционно там применяется коэффициент Бухгольца).
Коэффициент Бухгольца – способ определения мест (дополнительный коэффициент) в турнирах среди участников, набравших равное количество очков. Так же, как и коэффициент Бергера, применяется в играх, где за победу, ничью и поражение присуждается постоянное число очков. Однако, в отличие от коэффициента Бергера, который чаще всего применяется в круговых турнирах, коэффициент Бухгольца используется в турнирах, проводимых по швейцарской системе. В круговых турнирах система Бухгольца не применяется, т.к. в случае равенства очков в основном зачете, соперники будут иметь и равные коэффициенты.
Способ определения мест в соревнованиях среди участников, набравших равное количество очков, по коэффициенту Бухгольца был предложен в 1932 году и был назван по имени его изобретателя – шахматиста Бруно Бухгольца (Bruno Buchholz).
Коэффициент Бухгольца определенного участника складывается из суммы всех очков соперников, с которыми данный участник играл, независимо от результата встреч между ними. Идея заключается в том, что Участнику, игравшему с более сильными соперниками (соперниками, набравшими в сумме больше очков), присуждается более высокое итоговое место.
Усеченный коэффициент Бухгольца
Если у двух или более участников оказываются равными и количество набранных очков, и коэффициенты Бухгольца, то из коэффициента Бухгольца каждого участника вычитают результат соперника с меньшим количеством очков. Если после такого вычитания коэффициенты Бухгольца (без результата соперника с меньшим количеством очков) остаются равными, то процедура повторяется, то есть вычитают результат следующего слабейшего соперника и т.д.
Коэффициенты Бухгольца и Бергера изначально применялись только в турнирах по шахматам, однако, затем широко распространились и на другие игры, в которых результат строго фиксирован по набранным очкам (победа, поражение или ничья).
Примечание. К вопросу о расчете коэффициентов при пропуске тура и неявке соперника.
Как правило, используется следующий подход.
Все несыгранные партии (пропуск тура, неявка или нехватка соперника, «плюс») в целях подсчета коэффициентов условно считаются ничейными:
Коэффициент Бухгольца в шахматах
В шахматных турнирах, проходящих по швейцарской системе, определение победителя нередко проводится не просто по очкам, а с применением коэффициента Бухгольца. Эту систему подсчетов применяют в тех случаях, когда требуется выбрать лучшего среди претендентов с равным количеством набранных баллов. Она актуальна только для состязаний с большим количеством участников — более 30, подходит для применения в рамках open-турниров, где встречаются игроки с разным уровнем и опытом. О том, что такое коэффициент Бухгольца, как и зачем его считают, стоит поговорить более подробно.
Что это такое — коэффициент Бухгольца?
Вспомогательные коэффициенты для подсчета очков применяют в шахматах в тех случаях, когда прочие показатели у двух игроков равны. В турнирах по швейцарской системе этот метод носит имя немецкого шахматиста Бруно Бухгольца. В круговых состязаниях применяют другой коэффициент — Бергера. В случае с «Бухгольцем» в таблицах он обычно обозначается латиницей «BH».
Принцип подсчета максимально прост. У каждого игроков берется статистика игры его партнеров по турниру. Очки суммируются. Например, соперники набрали 3+5+4+4+2 каждый. Коэффициент Бухгольца у игрока составит 18. После этого подсчитываются очки соперников у другого претендента на победу. При большем коэффициенте игрок становится единоличным лидером турнирной таблицы.
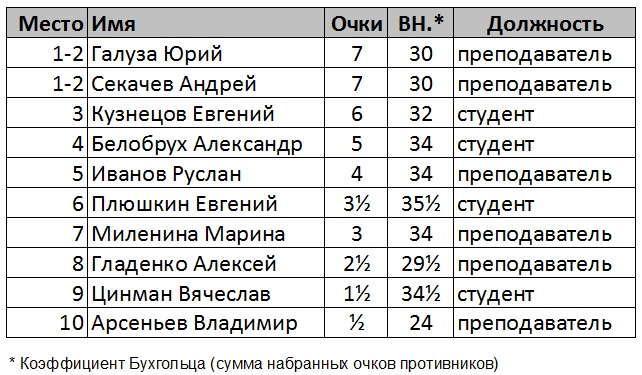
Если турнир проводится по швейцарской системе, коэффициент Бухгольца чаще всего рассчитывается сразу после каждой партии или дня с актуальными изменениями. Тогда в таблице результатов, помимо данных о количестве партий, числе побед, ничьих и поражений, появляется дополнительный столбец. В нем указывается коэффициент Бухгольца для каждого игрока, помогающий, в случае необходимости, обосновать расстановку результатов при определении итогового положения шахматиста в турнире.
Важно учесть, что свою важность этот элемент статистики приобретает только при равенстве по очкам. Соответственно, равный коэффициент Бухгольца не становится преимуществом, если у одного игрока 7 очков, а у другого 6. Основным показателем по-прежнему является число поражений и побед. Дополнительные коэффициенты применяются только в тех случаях, когда все партии сыграны, а определить лучшего по очкам не представляется возможным.
Как считается коэффициент Бухгольца
Система подсчета результатов в шахматах не приемлет полумер. Здесь используется всего 2 варианта начисления баллов:
Если в турнире нечетное количество участников, соперник не явился на игру или пропустил тур — это тоже учитывается. «Пострадавший» игрок получает техническую «ничью», как если бы он сыграл сам с собой с подобным результатом.
Использование дополнительных коэффициентов в шахматах — важная составляющая в распределении мест в турнирной таблице. Ситуация, когда сразу несколько участников имеют одинаковый результат, здесь нередка. В других видах спорта, где счет ведется по баллам, такая практика тоже довольно распространена. Например, у тяжелоатлетов берется за расчет разница в массе тела спортсменов и количестве попыток, использованных ими для подъема веса.
Логика коэффициента Бухгольца строится на простом утверждении: при равном количестве очков сильнее оказывается тот игрок, соперники которого показали в сумме более высокие результаты. Фактически, это означает, что игроку было сложнее добиться цели при прочих равных условиях. Утверждение не лишено логики, тем более что такая методика подсчетов вполне успешно работает.
При равном количестве очков и значений коэффициента применяется «усеченный Бухгольц». Из результатов вычитаются очки соперника с наименьшими показателями, затем они опять сверяются. Подсчеты продолжаются до тех пор, пока победитель не будет объявлен.
 Коэффициент Бергера
Коэффициент Бергера