выражение на порядок больше что это значит
Порядок, это сколько? Что значит на порядок выше, ниже?
Порядок, это сколько? Что значит на порядок выше, ниже?
Одно из понятий, которые большинством понимаются и употребляются неверно.
Но это от неграмотности!
Чтоб понять, что такое порядок, нужно обратится к математике, как нас учили в школе.
В математике словом порядок обычно называют количество цифр в числе. То есть если говорят на порядок выше и прибавить на порядок, то имеют ввиду, что цифр в записанном числе будет на одну больше, или меньше, если говорят уменьшилось на порядок. А что такое цифры, из которых состоит любое число. Самая правая цифра, показывает сколько в числе единиц, следующая сколько десятков, потом сотен, тысяч, десятков тысяч, сотен тысяч, миллионов. Каждая новая цифра увеличивает число на порядок, но если увеличение от 5 рублей до 50, на один порядок, не очень заметно, то увеличение ста тысяч до миллиона уже ощутимо. То есть порядок зависит от размера числа.
Так как у нас принята десятичная система исчисления, то порядок определяется десятками. Первый порядок- десятки, второй- сотни, третий тысячи и т.д. Соответственно на порядок выше, значит надо умножить на 10, на прядок ниже- разделить на 10.
Но часто эту фразу произносят люди далёкие от математики и по отношению к вещам, которые нельзя выразить в цифрах. К примеру, уровень знаний этого ученика на порядок выше, чем у других детей в классе. В большинстве таких случаев «на порядок выше» можно заменить на «намного лучше», «в несколько раз лучше» и тд.
Это слово, «порядок» пришло к нам из математики. Где используется десятичная система. На порядок выше, или на порядок ниже-это значит на порядок больше или меньше. А именно к числу прибавляется или отнимается о. То есть в десять раз.
В народе, может быть да, несколько неверно трактуют это понятие. Имея ввиду то, что «на порядок»-это «раза в два, ну может в три больше». А на самом деле это в десять раз. А на два порядка, это уже будет в сто раз.
поиск информации по открытым источникам 5 000 р
создание социально-психологического портрета личности 4 000 р
проверка » особых » обстоятельств ведения бизнеса 120 000 р
проверка юридических лиц 12 000 р
проверка физических лиц 7 000 р
Гранаты бывают очень разные по сортам, размерам, есть с косточками, есть совсем без косточек. Так что можно лишь приблизительно сказать сколько косточек в гранате. Если гранат бескостные, то можно сказать точнее- 0 косточек. А если с косточками, то их приблизительно 200.
Лекарственный препарат «Канефрон» используют при заболеваниях в урологии, назначают его в следующих случаях:
Заболевания являются серьезными, поэтому не стоит его применять для лечения самостоятельно.
Таким образом, лечащий врач должен вам назначить срок приема.
Если рассматривать общие рекомендации по приему, то они указывают, что принимать препарат можно в течение полугода, с небольшими перерывами. Курс должен состоять из приема канефорона в течение четырех недель, а затем одни неделя перерыва и снова повторяется такой прием. Даже возможно прием этого лекарства в течение 5-6 лет, но под строгим присмотром врача, обязательно узнавайте у него сколько вам времени нужно его пить.
Что значит «на порядок больше»?
Часто говорят «на порядок больше», «на порядок меньше» или даже «больше/меньше на несколько порядков». Интуитивно понятно, что «на порядок больше» означает «сильно больше», «значительно больше» — но вот хотелось бы знать, на сколько именно? Если прочитаете эту статью, будете знать точно.
Любое действительное число… Простите… Возможно, не все помнят, что это такое. А знаете — неважно. Как сказал дядюшка Мерфи: «Если вы не понимаете какой-либо термин в технической статье или документации, смело его пропускайте — статья полностью сохранит свой смысл и без этого термина».
Ноль, кстати, невозможно записать таким способом, потому что мантисса, по определению, не ноль, а десятку в какую целую степень ни возводи, всё равно получится число, большее ноля, а произведение двух чисел, не равных нулю, не равно нулю.
Такой вид записи числа называют научным или стандартным. Он удобен, например, тем, что числа, записанные в такой нотации, удобно сравнивать: если числа имеют один и тот же знак (оба положительные или оба отрицательные), то сначала сравниваются экспоненты, и только потом, если экспоненты равны, сравниваются мантиссы.
Подумаешь, скажете вы, открыл Америку! И так понятно: смотрим, какое число «длиннее» — то и больше! В общем — да. Интуитивно данное понятие уже входило в круг ваших понятий, в этой статье мы просто оформили их и придали им большую чёткость.
Ещё парочка примеров:
пять миллиардов на три порядка больше семи миллионов;
скорость чтения/записи данных на жёсткий диск (миллисекунды, 10^(-3)) на три порядка меньше скорости доступа к оперативной памяти (микросекунды, 10^(-6)).
Вот, в первом приближении, и всё. Теперь вы можете с уверенностью щеголять этим термином. Или просто употреблять его грамотно и к месту. Последнее, пожалуй, предпочтительнее.
Почему «в первом приближении»? Хм… Есть довольно известная в кругах программистов шутка: для программиста «на порядок» означает «в два раза». Почему в два? Мы же только что рассказали, что «на порядок» — это «в десять раз»? Как вам сказать… Есть один нюанс. Но это уже тема другого разговора.
Порядок выполнения действий, правила, примеры.
Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий.
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок:
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: 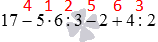
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени.
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Рассмотрим решения примеров.
Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.


 tverdyi_znak posting in
tverdyi_znak posting in  pishu_pravilno
pishu_pravilno На порядок больше?
На порядок больше?