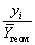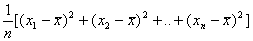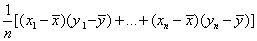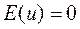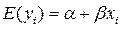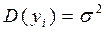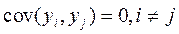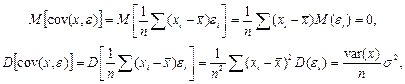второе условие гаусса маркова предполагает что дисперсия случайного числа
Второе условие гаусса маркова предполагает что дисперсия случайного числа
47. Всю совокупность реализаций случайной величины называют __________________ совокупностью.
• генеральной
49. Второе условие Гаусса-Маркова предполагает, что дисперсия случайного члена __________________ в каждом наблюдении.
• постоянна
50. Второй шаг метода Зарембки заключается в пересчете наблюдений y в новые 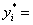
•
51. Выборочная дисперсия зависимой переменной регрессии равна __________________ объясненной дисперсии зависимой переменной и необъясненной дисперсии зависимой переменной.
• сумме
52. Выборочная дисперсия как оценка теоретической дисперсии имеет __________________ смещение.
• отрицательное
53. Выборочная дисперсия остатков в наблюдениях Var (y — (a + bx)) называется __________________ дисперсией зависимой переменной.
• необъясненной
54. Выборочная дисперсия рассчитывается по формуле: 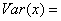
•
55. Выборочная дисперсия расчетных значений величины y называется __________________ дисперсией зависимой переменной.
• объясненной
56. Выборочная ковариация рассчитывается по формуле: 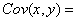
•
57. Выборочная корреляция является __________________ теоретической корреляции.
• оценкой
58. Гетероскедастичность заключается в том, что дисперсия случайного члена регрессии __________________ наблюдений.
• зависит от номера
59. Гетероскедастичность приводит к __________________ оценок параметров регрессии по МНК.
• неэффективности
60. Граничное значение области принятия гипотезы с p%-ной вероятностью совершить ошибку I рода определяется __________________ при p-процентном уровне значимости.
• критическим значением теста
Условия Гаусса-Маркова



Для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие из всех возможных результаты, случайная ошибка должна удовлетворять определенным условиям, известным как условия Гаусса-Маркова.
Понимание важности этих условий отличает компетентного исследователя от некомпетентного. Если условия не выполнены, надо это осознавать. А именно, если возможно, то провести корректирующие действия; если невозможно корректировка, то оценить, как невыполнение условий влияет на результат.
1-е условие Гаусса-Маркова состоит в том, что математическое ожидание случайной ошибки в любом наблюдении должно быть равно нулю:
Это означает, что иногда случайная ошибка будет положительной, иногда отрицательной, но она не должна иметь систематического смещения. Фактически, если уравнение регрессии включает свободный член, то разумно предположить, что это условие выполнено автоматически, так как роль константы состоит в определении любой систематической тенденции объясняемой переменной, которую не учитывают объясняющие переменные, включенные в уравнение регрессии.
Таким образом, если уравнение регрессии включает постоянную 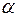
В терминах зависимой переменной условие 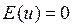
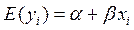
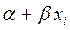
2-е условие Гаусса-Маркова состоит в том, что дисперсия ошибки постоянна для всех наблюдений:
Условие независимости дисперсии от номера наблюдения называется гомоскедастичностью (homoscedasticity). Случай непостоянства дисперсии для разных наблюдений называется гетероскедастичностью (heteroscedasticity). На рис.5 а) приведен пример типичной картинки для случая гомоскедастичности ошибок, на рис. 5 б) – пример данных с гетероскедастичными ошибками.
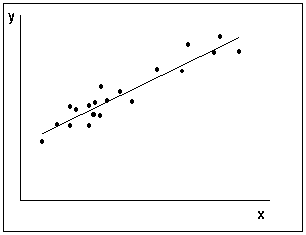 | 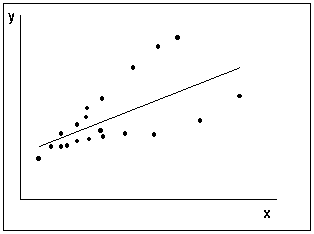 |
| а) гомоскедастичность ошибок | б) гетероскедастичность ошибок |
Рисунок 4 – Принципиальные схемы случаев гомоскедастичности и гетероскедастичности ошибок
Иногда случайная ошибка будет больше, иногда меньше, однако не должно быть такого, что в одних наблюдениях ошибка систематически больше, чем в других. Эта постоянная дисперсия обозначается σ 2 .
Если условие постоянства дисперсии не выполняется, то оценки, найденные по методу наименьших квадратов, будут неэффективны. Для получения более надежных результатов надо использовать модифицированный метод наименьших квадратов (см., например, Доугерти, 2001).
Величина σ 2 неизвестна. Одна из задач регрессионного анализа состоит в ее оценке, точнее оценке стандартного отклонения случайного члена.
Например, если случайная ошибка в одном наблюдении велика и положительна, то это не должно обусловливать систематическую тенденцию к тому, что в следующем наблюдении она будет обязательно мала и отрицательна (или велика и отрицательна, или мала и положительна). Случайные ошибки должны быть абсолютно независимы друг от друга, то есть ковариация между ними должна быть равна нулю.
Это условие часто нарушается в случае, когда наши данные являются временными рядами. В случае, когда условие некоррелированности ошибок не выполняется, то говорят об автокорреляции ошибок.
Типичная картинка автокорреляции ошибок представлена на рис. 6.
В терминах зависимой переменной условие отсутствия автокорреляции означает статистическую независимость значений y для разных наблюдений: cov(yi, yj)=0, i≠j.
Если третье условие не выполнено, то регрессия, оцененная методом наименьших квадратов, даст неэффективные результаты. Методы получения более надежных результатов представлены, например, в учебнике Кристофера Доугерти (2001).
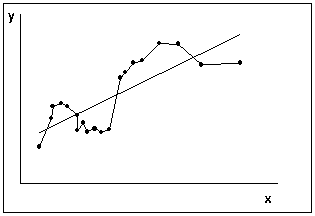 | 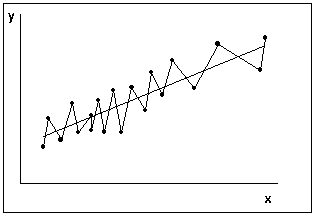 |
| а) ковариация ошибок положительна | б) ковариация ошибок отрицательна |
Рисунок 5 – Принципиальные схемы автокорреляции ошибок
4-е условие Гаусса-Маркова – случайная ошибка должна быть распределена независимо от объясняющих переменных.
Значение объясняющей переменной x в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.
Во многих случаях используется более сильное условие: объясняющие переменные не являются стохастическими.
Предположение о нормальности распределения ошибок часто используется одновременно с условиями Гаусса-Маркова:
При соблюдении перечисленных пяти условий регрессионная модель (41) называется классической нормальной линейной регрессионной моделью.
Итак, мы имеем набор данных (xi,yi) i=1…n, и классическую линейную регрессионную модель (выполняются четыре условия Гаусса-Маркова). Задача – оценить параметры модели α, β и дисперсию ошибки σ 2 «наилучшим» способом, то есть найти несмещенные эффективные состоятельные оценки.
В предположениях классической линейной регрессии модели:
1) 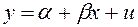
где x – неслучайная величина; y, u – случайные величины.
2)
3)
4)
оценки а и b для параметров α и β, полученные по методу наименьших квадратов, имеют наименьшую дисперсию среди всех линейных несмещенных оценок, то есть аиb несмещенные эффективные оценки.
Таким образом, оценки а и b являются наилучшими в статистическом смысле.
4.6.3. Оценка дисперсии ошибок σ 2
Имеем 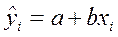
Тогда 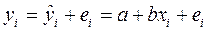
Не следует путать остатки ei с ошибками ui. Остатки тоже случайные величины, однако остатки ei наблюдаемы в отличие от ошибок ui.
Можно доказать, что 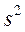
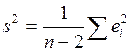 | (42) |
4.6.4. Оценка дисперсий параметров модели a и b
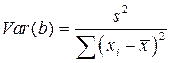 . . | (43) |
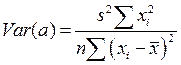 . . | (44) |
Стандартное отклонение оценки коэффициента регрессии:
Предпосылки регрессионного анализа. Условия Гаусса-Маркова
Глава 3. Свойства коэффициентов регрессии и проверка гипотез
Случайные составляющие коэффициентов регрессии
Величина Y в модели регрессии Y = a + b× X + e имеет две составляющие: неслучайную (a + b×X) и случайную (e).
Оценки коэффициентов регрессии (a; b)являются линейными функциями Y и теоретически их также можно представить в виде двух составляющих.
Воспользовавшись разложением показателей:

получим преобразованные соотношения для (a; b):

Таким образом, коэффициенты (a; b) разложены на две составляющие:
неслучайную, равную истинным значениям (a; b) и случайную, зависящую от e.
На практике нельзя разложить коэффициенты регрессии на составляющие, т.к. значения (a; b) или фактические значения e в выборке неизвестны.
Предпосылки регрессионного анализа. Условия Гаусса-Маркова
Линейная регрессионная модель с двумя переменными имеет вид:
где Y –объясняемая переменная, X – объясняющая переменная, e – случайный член.
Для того, чтобы регрессионный анализ, основанный на МНК давал наилучшие из всех возможных результаты, должны выполняться условия Гаусса-Маркова.
1.Математическое ожидание случайного члена в любом наблюдении должно быть равно нулю
2. Дисперсия случайного члена должна быть постоянной для всех наблюдений
3. Случайные члены должны быть статистически независимы (некоррелированы) между собой
4.Объясняющая переменнаяxi естьвеличина неслучайная.
При выполнении условий Гаусса-Маркова модель называется классической нормальной линейной регрессионной моделью.
Наряду с условиями Гаусса-Маркова обычно предполагается, что случайный член распределен нормально, т.е. ei
Замечание. Если случайный член имеет нормальное распределение, то требование некоррелированности случайных членов эквивалентно их независимости.
Рассмотрим подробнее условия и предположения, лежащие в основе регрессионного анализа.
Первое условие означает, что случайный член не должен иметь систематического смещения. Если постоянный член включен в уравнение регрессии, то это условие автоматически выполняется.
Второе условиеозначает, что дисперсия случайного члена в каждом наблюдении имеет только одно значение.
Под дисперсией s 2 имеется в виду возможное поведение случайного члена до того, как сделана выборка. Величина s 2 неизвестна, и одна из задач регрессионного анализа состоит в её оценке.
Условие независимости дисперсии случайного члена от номера наблюдения называется гомоскедастичностью (что означает одинаковый разброс). Зависимость дисперсии случайного члена от номера наблюдения называется гетероскедастичностью.
Характерные диаграммы рассеяния для двух случаев показаны на рис. 9,а и б соответственно.
Если условие гомоскедастичности не выполняется, то оценки коэффициентов регрессии будут неэффективными, хотя и несмещенными.
Существуют специальные методы диагностирования и устранения гетероскедастичности.
Третье условиеуказывает на некоррелированность случайных членов для каждых двух соседних наблюдений. Это условие часто нарушается, когда данные являются временными рядами. В случае, когда третье условие не выполняется, говорят об автокорреляции остатков.
Типичный вид данных при наличии автокорреляции показан на рис. 10.
|
Если условие независимости случайных членов не выполняется, то оценки коэффициентов регрессии, полученные по МНК, оказываются неэффективными,хотя и несмещенными.
Существуют методы диагностирования и устранения автокорреляции.
Четвертое условиео неслучайностиобъясняющей переменной является особенно важным.
Если это условие нарушается, то оценки коэффициентов регрессии оказываются смещенными и несостоятельными.
Нарушение этого условие может быть связано с ошибками измерения объясняющих переменных или с использованием лаговых переменных.
В регрессионном анализе часто вместо условия о неслучайности объясняющей переменной используется более слабое условие о независимости (некоррелированности) распределений объясняющей переменной и случайного члена.Получаемые при этом оценки коэффициентов регрессии обладают теми же основными свойствами, что и оценки, полученные при использовании условия о неслучайности объясняющей переменной.
Предположение о нормальности распределения случайного члена необходимо для проверки значимости параметров регрессии и для их интервального оценивания.
Теорема Гаусса-Маркова
Теорема Гаусса-Маркова. Если условия 1-4 регрессионного анализа выполняются, то оценки (a, b), сделанные с помощью МНК, являются наилучшими линейными несмещенными оценками, т.е. обладают следующими свойствами:
несмещенности: M(a) = a, M(b) = b, что означает отсутствие систематической ошибки в положении линии регрессии;
эффективности: имеют наименьшую дисперсию в классе всех линейных несмещенных оценок, равную

состоятельности: 
Для проверки выводов теоремы воспользуемся оценками (a, b) в виде разложения (3.1) и соотношением

Пусть x не случайная величина, тогда
Вычислим математическое ожидание и дисперсию оценок b, a:
Второе условие гаусса маркова предполагает что дисперсия случайного числа
2.3. Статистические свойства оценок метода наименьших квадратов
Поскольку полученные оценки a и b коэффициентов линейной регрессии основаны на статистических данных и являются случайными величинами, то естественно установить свойства этих оценок, как случайных величин. Более того, не выяснив этих свойств, невозможно сделать обоснованных выводов относительно качества и надежности полученных оценок. Необходимо, в частности, определить такие их статистические характеристики, как математическое ожидание и дисперсия. К желательным свойствам оценок относятся также несмещенность и состоятельность. Далее, если бы удалось определить вид распределения (плотности распределения) оценок, можно было бы построить доверительные интервалы для истинных значений параметров регрессии (то есть получить интервальные оценки коэффициентов) и реализовать процедуры проверки гипотез относительно их значений. Важную роль играет также изучение статистических свойств остатков оцененной регрессии.
Все эти задачи можно решить, основываясь на некоторых правдоподобных теоретических предпосылках (гипотезах) модели, выполнение которых на практике подлежит проверке с помощью специально разработанных для этого статистических процедур.
Предположение относительно независимых переменных
Предположения относительно случайной составляющей модели
При выполнении предпосылки относительно переменной x статистические свойства оценок параметров и зависимой переменной, а также остатков, целиком определяются вероятностными свойствами случайной составляющей регрессионной модели. Относительно случайной составляющей в классическом регрессионном анализе предполагают выполнение следующих условий, которые называются условиями Гаусса-Маркова и играют ключевую роль при изучении свойств оценок, полученных по методу наименьших квадратов.
1. Первое условие заключается в том, что математическое ожидание случайной составляющей во всех наблюдениях должно быть равно нулю. Формально это записывается так
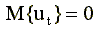 , для всех t =1,2,…,n. , для всех t =1,2,…,n. |
Смысл этого условия заключается в том, что не должно быть систематического смещения случайной составляющей. В линейной регрессии систематическое смещение линии регрессии учитывается с помощью введения параметра смещения 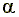
2. Дисперсия случайной составляющей постоянна для всех наблюдений (то есть не зависит от номера наблюдения). Это условие записывается так
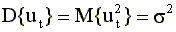 , где дисперсия , где дисперсия 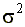 — величина постоянная. — величина постоянная. |
Это свойство дисперсии ошибок называется гомоскедастичностью (однородностью) (запомните этот термин).
Графическая иллюстрация понятий гомоскедастичность и гетероскедастичность
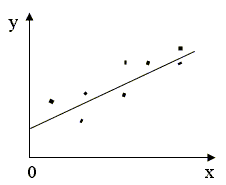
Рис. 2.6а. Гомоскедастичность
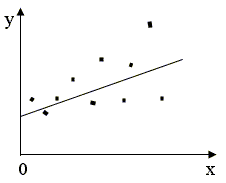
Рис. 2.6б. Гетероскедастичность
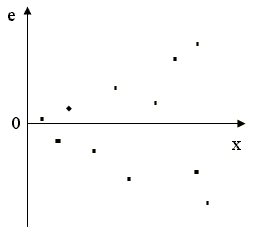
Рис. 2.6в. Гетероскедастичность
3. Случайные составляющие модели для различных наблюдений некоррелированы. Это условие записывается таким образом
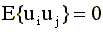 , для всех i не равных j (i, j=1,2,…,n). , для всех i не равных j (i, j=1,2,…,n). |
Выполнение этого условия означает отсутствие систематической (статистической) связи между значениями случайного члена в любых двух наблюдениях. Это свойство на практике также проверяется с помощью статистических процедур на основе анализа остатков модели. Если оно нарушается, то процедура оценки параметров должна быть скорректирована.
4. Четвертое условие Гаусса-Маркова записывается так
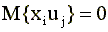 , для всех i и j, , для всех i и j, |
и означает, что объясняющие переменные и случайные составляющие некоррелированы для всех наблюдений. Ранее мы предположили, что объясняющая переменная в модели не является стохастической. В этом случае четвертое условие выполняется автоматически.
Дополнительное предположение о нормальном распределении ошибок
Данное предположение является, пожалуй, наиболее спорным. Дело в том, что предположение о нормальности можно считать правдоподобным, если значения случайной величины порождаются в результате воздействия большого количества независимых случайных факторов, каждый из которых не обязательно имеет нормальное распределение. Примером такого воздействия является так называемое броуновское движение (хаотичное движение малых частиц в жидкости как результат совокупного воздействия на частицу (ударов, соударения) большого количества молекул жидкости).
Если случайные величины в модели распределены по нормальному закону, то из свойств некоррелированности в третьем и четвертом условиях Гаусса-Маркова следует и независимость соответствующих случайных величин.
2.3.2. Свойства выборочных вариаций и ковариаций. Остаточные ошибки (остатки) модели, их свойства
Свойства выборочных вариаций (дисперсий) и ковариаций
Для дальнейшего изложения нам понадобиться установить ряд правил, которые можно использовать при преобразовании выражений, содержащих выборочные вариации и ковариации.
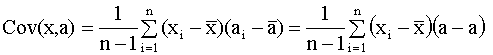 , , |
откуда следует свойство
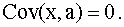
Далее, нетрудно видеть, что имеют место равенства