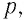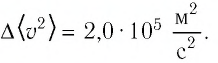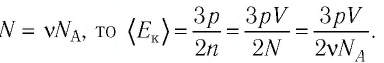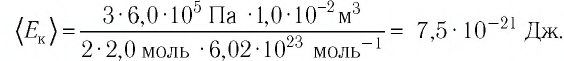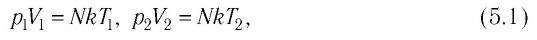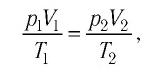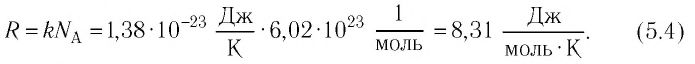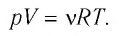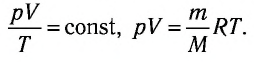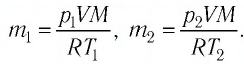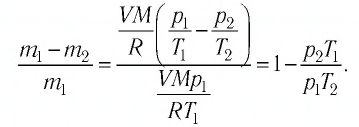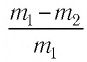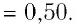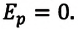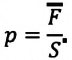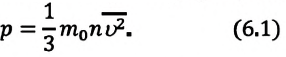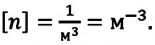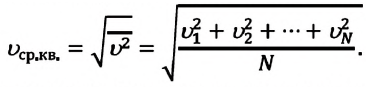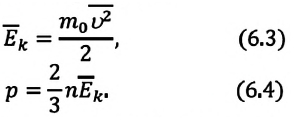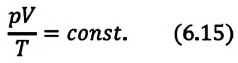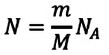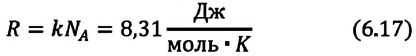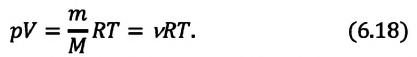вследствие чего возникает давление газа

Давление газа на стенки сосуда

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Газ: агрегатное состояние

В мире есть три агрегатных состояния — твердое, жидкое и газообразное. Их характеристики — в таблице

Агрегатные состояния

Свойства

Расположение молекул

Расстояние между молекулами

Движение молекулы

сохраняет форму и объем

в кристаллической решетке

соотносится с размером молекул

колеблется около своего положения в кристаллической решетке

близко друг к другу

малоподвижны, при нагревании скорость движения молекул увеличивается

занимают предоставленный объем

больше размеров молекул

хаотичное и непрерывное

В жизни мы встречаем газообразное состояние вещества, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (он занимает весь предоставленный ему объем), состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.

Давление газа

Мы только что выяснили, что молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.

Например, в комнате, в которой вы сейчас находитесь, на каждый квадратный сантиметр за 1 с молекулами воздуха наносится столько ударов, что их количество выражается двадцати трехзначным числом.

Хотя сила удара отдельной молекулы мала, действие всех молекул о стенки сосуда приводит к значительному давлению. Это как если бы один комар толкал машину, то она бы и не сдвинулась с места, а вот пару сотен миллионов комаров вполне себе способны эту машину сдвинуть.

Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.

Зависимость давления от других величин

Зависимость давления от объема

В механике есть формула давления, которая показывает: давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.

Давление
p = F/S

p — давление [Па]
F — сила [Н]
S — площадь [м^2]

То есть, если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы они толкали грузовой автомобиль (просто потому что легковая меньше грузовика).

Из формулы давления следует, что давление на легковой автомобиль будет больше из-за меньшей площади.

Давайте рассмотрим аналогичный пример с двумя сосудами разной площади.

Давление в левом сосуде будет больше, чем во втором, по аналогичной схеме — потому что площадь меньше. Но если площадь основания меньше, то и объем меньше. Это значит, что давление будет зависеть от объема следующим образом: чем больше объем, тем меньше давление — и наоборот.

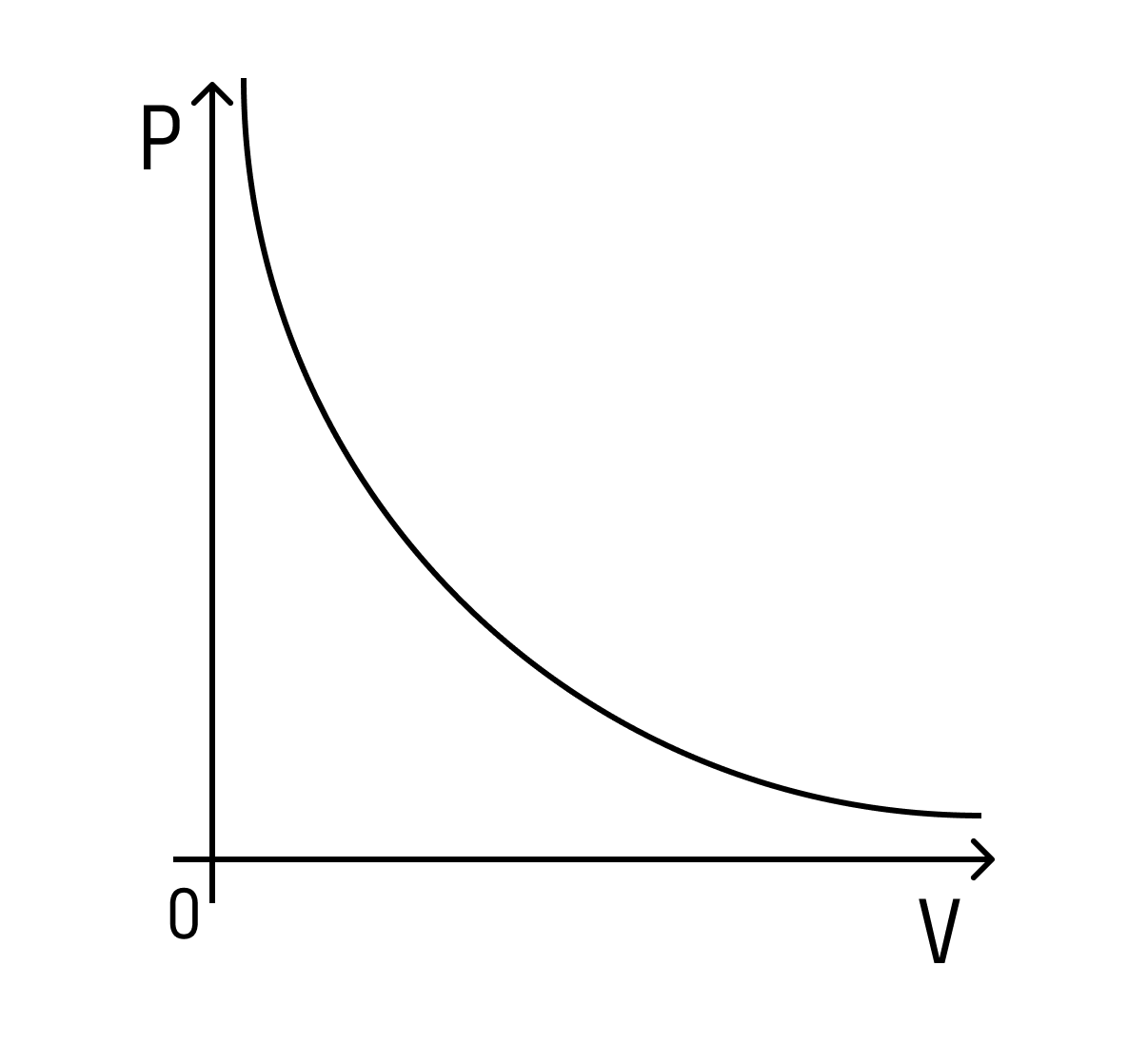
При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):

Такая зависимость называется законом Бойля-Мариотта.

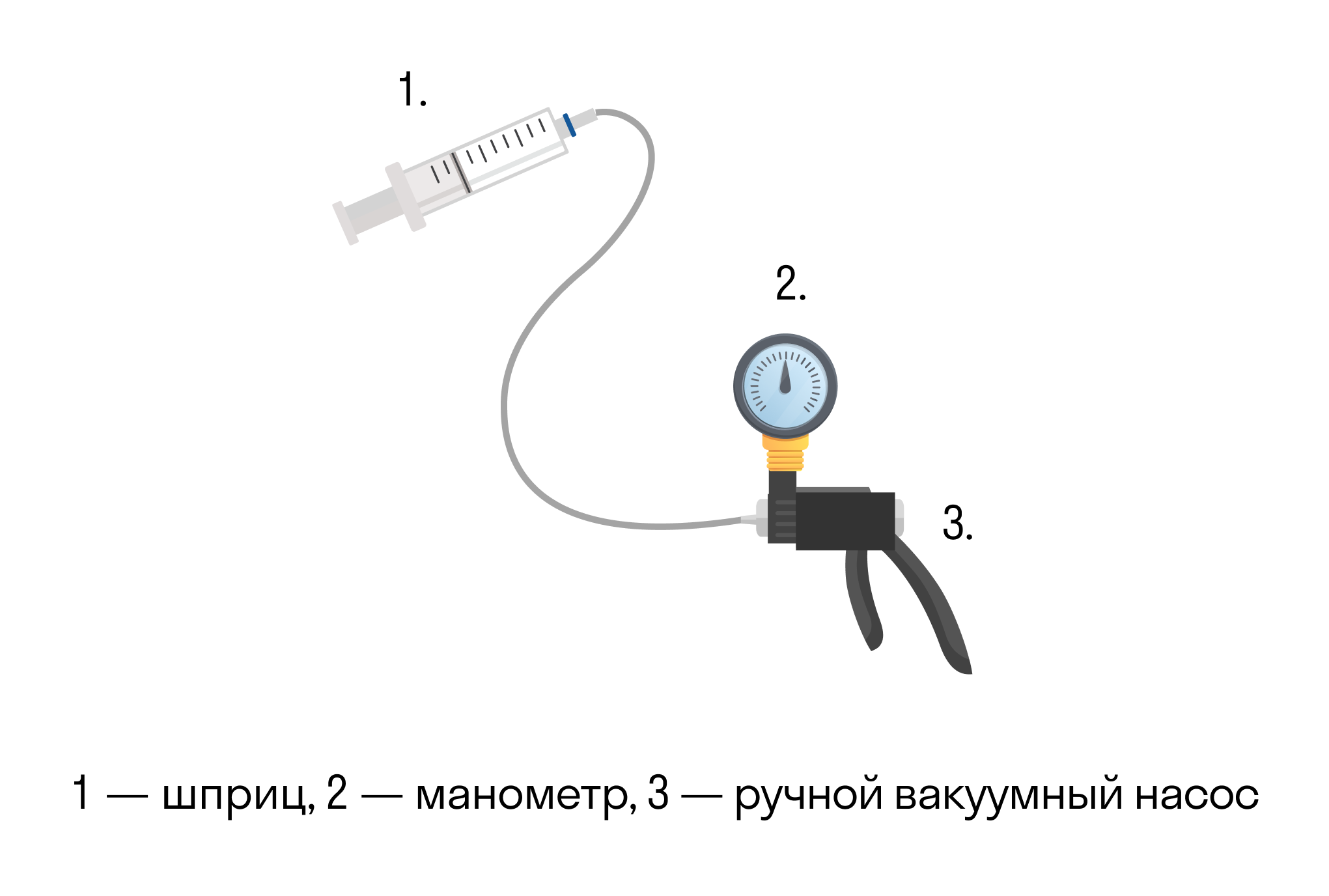
Она экспериментально проверяется с помощью такой установки.

Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.

Зависимость давления от температуры

Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Эти исследования были впервые произведены в Жаком Шарлем.

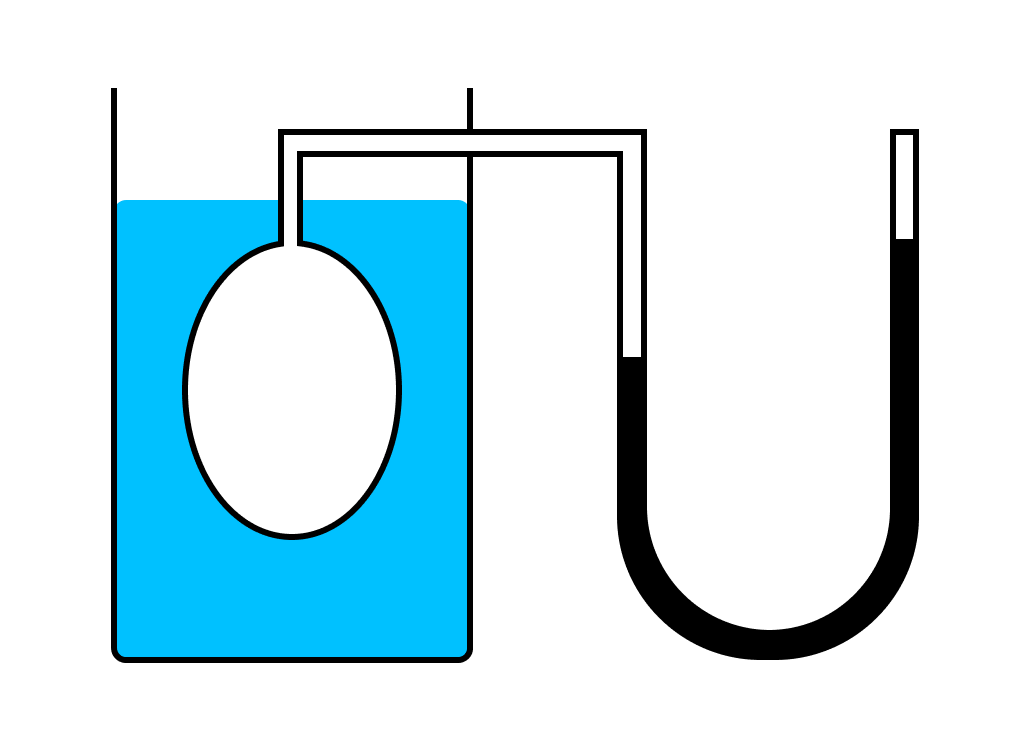
Газ нагревался в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Пренебрегая ничтожным увеличением объема колбы при нагревании и незначительным изменением объема при смещении ртути в узкой манометрической трубке.

Таким образом, можно считать объем газа неизменным. Подогревая воду в сосуде, окружающем колбу, измеряли температуру газа по термометру, а соответствующее давление — по манометру.

Этот эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.

С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейно:

Эта зависимость называется законом Шарля.

Хранение и транспортировка газов

Если нужно перевезти значительное количество газа из одного места в другое, или когда газы необходимо длительно хранить — их помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.

Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.

Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или любым способом пытаться сделать в них отверстие, даже после использования.

Источник

Содержание:

Идеальный газ:

Наиболее простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ начинают с газов. Газ (греч. chaos — хаос) — такое агрегатное состояние вещества, когда составляющие его частицы почти свободно и хаотически движутся между соударениями, во время которых происходит резкое изменение их скорости. Термин «газ» предложил в начале XVII в. нидерландский химик Ян Батист ван Гельмонт (1579— 1644).

Макро- и микропараметры:

При изучении механики в 9-м классе вы познакомились с понятием «состояние механической системы тел». Параметрами этого состояния являются координаты, скорости или импульсы тел. В тепловых процессах основными физическими величинами, характеризующими состояние макроскопических тел без учёта их молекулярного строения, являются давление

Одна из важнейших задач молекулярно-кпнетической теории состоит в установлении связи между макроскопическими и микроскопическими параметрами.

Идеальный газ

Для теоретического объяснения свойств газов используют их упрощённую модель — идеальный газ.

Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия их взаимодействия равна нулю); силы действуют только во время столкновений молекул, причём это силы отталкивания.

Поведение молекул идеального газа можно описать, используя законы Ньютона и учитывая, что между соударениями молекулы движутся практически равномерно и прямолинейно.

Модель идеального газа можно использовать в ограниченном диапазоне температур и при достаточно малых давлениях. Так, например, свойства водорода и гелия при нормальном атмосферном давлении и комнатной температуре близки к свойствам идеального газа.

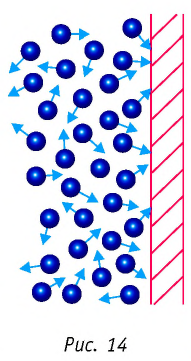
Изучая физику в 7-м классе, вы узнали, что давление газа на стенки сосуда, в котором он находится, как и на любое тело, помещённое внутрь сосуда, создаётся в результате ударов частиц, образующих газ (рис. 14). Вследствие хаотичности их движения усреднённое по времени давление газа в любой части сосуда одинаково, и его можно определить по формуле

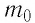
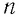
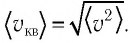
Выражение (3.1) называют основным уравнением молекулярно-кинетической теории идеального газа. Это уравнение позволяет рассчитать макроскопический параметр давление р идеального газа через массу молекулы, концентрацию молекул и среднюю квадратичную скорость их теплового движения, определяемую по формуле Формула (3.1) связывает между собой макро- и микроскопические параметры системы «идеальный газ».

Зависимость давления газа от среднего значения квадрата скорости 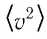теплового движения его молекул обусловлена тем, что с увеличением скорости, во-первых, возрастает импульс молекулы, а следовательно, и сила удара о стенку. Во-вторых, возрастает число ударов, так как молекулы чаще соударяются со стенками.

Обозначим через 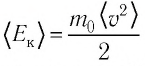среднюю кинетическую энергию поступательного движения молекул. Тогда основное уравнение молекулярно-кинетической теории примет вид:

Из выражения (3.2) следует, что давление идеального газа зависит от средней кинетической энергии поступательного движения его молекул и их концентрации.

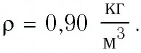
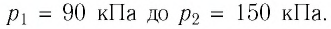
Баллон электрической лампы наполнен газом, плотность которого После включения лампы давление газа в ней увеличилось от Определите, на сколько при этом увеличился средний квадрат скорости теплового движения молекул газа.

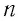
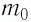
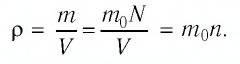
Решение. Покажем, что между плотностью р газа и концентрацией его частиц существует связь. Плотность вещества газа равна отношению массы к предоставленному ему объёму. Поскольку произведение массы одной молекулы и числа N молекул равно массе вещества, то:

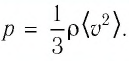
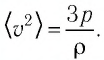
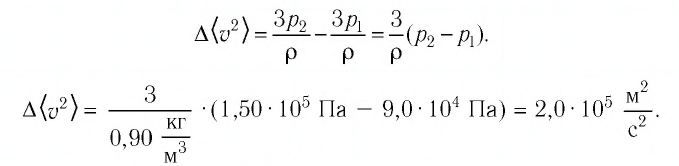
Тогда основное уравнение молекулярно-кинетической теории можно записать в виде: Следовательно, средний квадрат скорости теплового движения молекул газа Определим изменение среднего квадрата скорости теплового движения молекул газа после включения лампы:

Ответ:

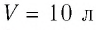
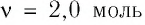
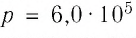
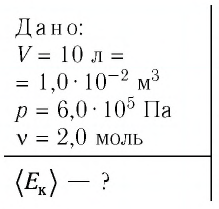
В сосуде вместимостью находится одноатомный газ, количество вещества которого и давление Па. Определите среднюю кинетическую энергию теплового движения атомов этого газа.

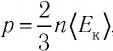
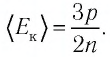
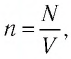
Решение. Из основного уравнения молекулярно-кинетической теории, записанного в виде , следует, что Так как концентрация атомов а число атомов газа

Ответ:

Уравнение состояния идеального газа

Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.

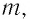
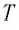
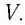
Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление р, масса температура и объём Уравнение, связывающее параметры данного состояния, называют уравнением состояния системы. Изменение параметров состояния системы с течением времени называют процессом.

Если при переходе идеального газа из одного состояния в другое число его т

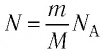
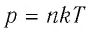
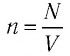
молекул остается постоянным, т. е. масса и молярная масса газа не изменяются, то из уравнений и следует:

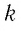
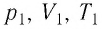
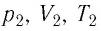
где — постоянная Больцмана; — параметры начального состояния газа, а — конечного. Из соотношений (5.1) следует, что

При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.

Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.

Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799—1864), поэтому его называют уравнением Клапейрона.

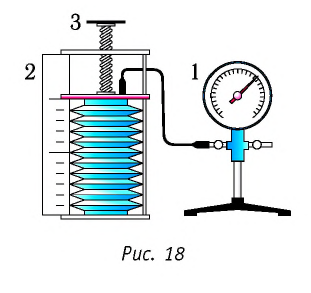
В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.

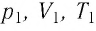
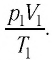
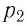
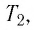
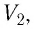
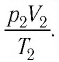
Измерив параметры газа в начальном состоянии, вычисляют отношение Затем помещают сосуд в горячую воду. При этом температура газа и его давление изменяются. Вращая винт 3, изменяют вместимость сосуда. Измерив снова давление газа и температуру а также рассчитав предоставленный ему объём вычисляют отношение Как показывают расчёты, уравнение состояния (5.2) выполняется в пределах погрешности эксперимента.

Уравнение состояния (5.2) можно применять для газов при следующих условиях:

Поскольку число частиц 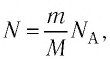то из уравнения (5.1) следует:

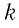
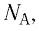
Величину, равную произведению постоянной Больцмана и постоянной Авогадро назвали универсальной газовой постоянной R:

С учётом выражения (5.4) уравнение (5.3) примет вид:

Поскольку количество вещества 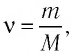то формулу (5.5) можно записать в виде:

Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834—1907) в 1874 г., поэтому его называют уравнением Клапейрона—Менделеева.

Отметим, что уравнение Клапейрона—Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона-Менделеева, можно описать различные процессы, происходящие в идеальном газе.

Давление смеси газов

В повседневной жизни часто приходится иметь дело не с газом, состоящим из одинаковых молекул, а со смесью нескольких разнородных газов, не вступающих в химические реакции при рассматриваемых условиях. Например, воздух в комнате является смесью азота, кислорода, инертных газов и водорода, а также некоторых других газов.

Вследствие теплового движения частиц каждого газа, входящего в состав газовой смеси, они равномерно распределяются по всему предоставленному смеси объёму. Столкновения частиц обеспечивают в смеси тепловое равновесие.

Каждый газ вносит свой вклад в суммарное давление, производимое газовой смесью, создавая давление, называемое парциальным.

Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.

Смесь идеальных газов принимают за идеальный газ.

Из истории физики:

Фундаментальные исследования газовых смесей провёл английский учёный Джон Дальтон (1766-1844). Им сформулирован закон независимости парциальных давлений компонентов смеси (1801-1802). В 1802 г. на несколько месяцев раньше французского учёного Жозефа Гей-Люссака (1778-1850) Дальтон установил закон теплового расширения газов, а также ввёл понятие атомного веса.

При постоянных массе и молярной массе отношение произведения давления идеального газа и его объёма к абсолютной температуре является величиной постоянной (уравнение состояния идеального газа):

Парциальное давление — давление газа, входящего в состав газовой смеси, если бы он один занимал весь объём, предоставленный смеси, при той же температуре.

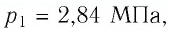
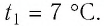
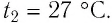
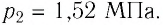
Баллон с газом, давление которого находился в неотапливаемом помещении, где температура воздуха После того как некоторое количество газа было израсходовано, баллон внесли в помещение, где температура воздуха Определите, какая часть газа была израсходована, если после длительного пребывания баллона в отапливаемом помещении давление газа в нём стало

Решение. Если пренебречь тепловым расширением баллона, то его вместимость не изменяется. Запишем уравнение Клапейрона—Менделеева для начального и конечного состоянии газа, считая его идеальным:

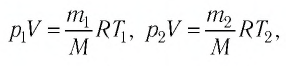
откуда

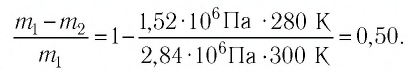
Ответ:

Основное уравнение молекулярно-кинетической теории идеального газа

В молекулярной физике изучаются свойства вещества во всех агрегатных состояниях, в том числе и газообразном. В природе почти нет отдельно взятого газа, реальный газ атмосферы представляют собой сложную систему разных газов.

Идеальный газ:

Первый шаг в создании любой физической теории состоит в построении идеализированной модели реального объекта. Такая модель всегда имеет упрощенный вид действительности, и с ее помощью изучаются количественные и качественные закономерности и свойства реального объекта с учетом определенных ограничений.

Поэтому идеальный газ можно сколько угодно сжимать; —только при соударении молекул друг с другом или со стенками сосуда между ними возникают силы отталкивания;

Свойства идеального газа характеризуются микроскопическими и макроскопическими параметрами и связями между ними.

Макроскопическими являются такие параметры газа, как ее давление, объем и температура, определяющие свойства газа в целом.

Основной задачей молекулярно-кинетической теории является установление взаимной связи между микроскопическими параметрами, характеризующими молекулы газа, и макроскопическими (измеряемыми) величинами, характеризующими газ.

Основное уравнение молекулярно-кинетической теории идеального газа:

Известно, что давление газа возникает в результате многочисленных непрерывных и беспорядочных соударений молекул газа о стенки сосуда, в котором он находится. Это давление равно среднему значению модуля равнодействующей силы, приходящейся на единицу площади:

В 1857 г. немецкий физик Рудольф Клаузиус (1822-1888), используя модель идеального газа, определил уравнение для давления газа, называемое основным уравнением молекулярно-кинетической теории идеального газа.

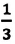
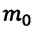
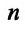
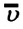
Где — количественный коэффициент, характеризующий трехмерность пространства и выражающий равноправность всех трех направлений в хаотическом движении молекул, — масса одной молекулы, — концентрация молекул, — средняя квадратичная скорость молекул.

Концентрация молекул — это число молекул в единице объема:

Единица концентрации в СИ:

Средняя квадратичная скорость молекул равна корню квадратному из средней арифметической величины квадратов скоростей отдельных молекул:

Так как среднее значение квадрата скорости молекул связано со средним значением кинетической энергии их поступательного движения, то, следовательно, и давление идеального газа зависит от среднего значения кинетической энергии молекул:

Давление идеального газа прямо пропорционально концентрации молекул и среднему значению кинетической энергии молекул.

Если принять во внимание, что плотность газа 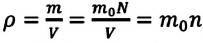в (6.1), то получится формула зависимости давления идеального газа от ее плотности:

Вы исследовали идеальный газ с позиций MKT и определили связь между его макроскопическими и микроскопическими параметрами.

Уравнение Клапейрона

Связь между тремя макроскопическими параметрами (давление, объем и температура), характеризующими состояние идеального газа, определяет уравнение состояние идеального газа.

Если число молекул идеального газа остается постоянным, то есть масса и молярная масса не меняются, то при переходе идеального газа из одного состояния в другое, из формул (6.2) и (6.9) имеем для этих состояний:

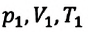
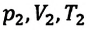
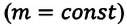
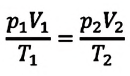
Где — параметры идеального газа в начальном состоянии, — параметры идеального газа в конечном состоянии. При помощи простых математических преобразований выражений (6.14) для идеального газа данной массы получим:

или

Это уравнение (6.15), характеризующее состояние идеального газа, впервые в 1834 году получил французский физик Бенуа Клапейрон (1799-1864), поэтому его назвали уравнением Клапейрона.

Отношение произведения давления идеального газа данной массы на его объем к абсолютной температуре является постоянной величиной.

Уравнение Менделеева-Клапейрона:

Приняв во внимание формулу, связывающую число частичек вещества, общую массу вещества, молярную массу и число Авогадро,

в формуле (6.14), получим:

Произведение постоянной Больцмана на постоянную Авогадро также является постоянной величиной. Оно называется универсальной газовой постоянной, обозначается буквой 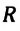и имеет числовое значение:

Приняв во внимание выражение (6.17) в (6.16), получаем выражение, характеризующее состояние идеального газа и называемое уравнением Менделеева-Клапейрона.

Физический смысл универсальной газовой постоянной определяется из последнего выражения.

Универсальная газовая постоянная равна отношению произведения давления и объема к абсолютной температуре одного моля любого газа.

Уравнение Менделеева-Клапейрона можно записать и в таком виде:

Где 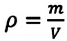— плотность газа.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник