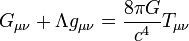временного континуума что это
Может ли квантовая механика объяснить существование пространства-времени?
Квантовая механика странная. Для нас, существ, не способных видеть микромир не вооруженным глазом, представить себе как все устроено на уровне атомов довольно сложно. Между тем, согласно атомной теории, все во Вселенной состоит из мельчайших частиц – атомов, скрепленных друг с другом электрическими и ядерными силами. Физические эксперименты, проведенные в ХХ веке показали, что атомы можно дробить на еще более мелкие, субатомные частицы. В 1911 году британский физик Эрнест Резерфорд провел ряд экспериментов и пришел к выводу, что атом похож на Солнечную систему, только по орбитам вместо планет вокруг него вращаются электроны. Два года спустя, взяв за основу модель Резерфорда, физик Нильс Бор изобрел первую квантовую теорию атома и в этой области теоретической физики все стало еще сложнее. Но если квантовая механика объясняет как взаимодействуют между собой мельчайшие частицы, может ли она объяснить существование пространства-времени?
Ученые ищут ответ на вопрос о том из чего состоит пространство-время уже много лет, но пока безуспешно
Что такое пространство-время?
Уверена, большинство из нас воспринимают пространственно-временной континуум как нечто, само собой разумеющееся. И в этом нет ничего удивительного, ведь не каждый день мы размышляем над чем-то подобным. Но если хорошенько задуматься, то окажется, что ответить на вопрос о том, что представляет собой пространство-время не так уж просто.
Начнем с того, что в соотвествии с теорией относительности (ОТО) Эйнштейна, Вселенная имеет три пространственных измерения и одно временное измерение. При этом все четыре измерения органически связаны в единое целое, являясь почти равноправными и в определенных рамках и условиях способными переходить друг в друга. В свою очередь пространственно-временной континуум или пространство-время – это физическая модель, дополняющая пространство временным измерением.
В рамках общей теории относительности пространство-время также имеет единую динамическую природу, а его взаимодействие со всеми остальными физическими объектами и есть гравитация.
В рамках ОТО теория гравитации и есть теория пространства-времени, которое не является плоским и способно менять свою кривизну.
Из ОТО также следует, что гравитация является результатом массы, такой как планета или звезда, искажающая геометрию пространства-времени. Космический аппарат NASA Gravity Probe, запущенный в 2004 году, точно измерил, насколько гравитация Земли искривляет пространство-время вокруг нее, в конечном итоге подтвердив расчеты Эйнштейна. Но откуда взялось пространство-время? Ответ, как это ни странно, может скрывать в себе квантовая механика.
Квантовая механика и теория гравитации
Как пишет портал Astronomy.com, сегодня физики стоят на пороге революции, которая может привести к пересмотру всего что мы знаем о пространстве-времени и, возможно, к объяснению того, почему квантовая механика кажется такой странной.
«Пространство-время и гравитация должны в конечном итоге возникнуть из чего-то другого», – пишет физик Брайан Свингл из Университета Мэриленда в статье, опубликованной в журнале Annual Review of Condensed Matter Physics. Иначе трудно понять, как гравитация Эйнштейна и математика квантовой механики могут примирить их давнюю несовместимость.
Квантовая механика противоречит ОТО
Взгляд Эйнштейна на гравитацию как проявление геометрии пространства-времени был чрезвычайно успешным. Но то же самое относится и к квантовой механике, которая с безошибочной точностью описывает махинации материи и энергии на атомном уровне. Однако попытки найти математическое решение, которое совместило бы квантовую странность с геометрической гравитацией, наталкивались на серьезные технические и концептуальные препятствия.
Хотите всегда быть в курсе последних новостей из мира популярной науки и высоких технологий? Подписывайтесь на наш новостной канал в Google News чтобы не пропустить ничего интересного.
По крайней мере, так было долгое время при попытках понять обычное пространство-время. Возможный ответ пришел из теоретического изучения альтернативных геометрий пространства-времени, мыслимых в принципе, но обладающих необычными свойствами. Одна из таких альтернатив известна как антидеситтеровское пространство, которое имеет тенденцию сжиматься само по себе, а не расширяться, как это делает Вселенная. Для жизни, безусловно, это было бы не самое приятное место. Но как лаборатория для изучения теорий квантовой гравитации, оно может многое предложить и даже стать ключом к квантовым процессам, которые могут быть ответственны за создание пространства-времени.
Что такое антидеситтеровское пространство?
Исследования антидеситтеровское пространства предполагают, например, что математика, описывающая гравитацию (то есть геометрию пространства-времени), может быть эквивалентна математике квантовой физики в пространстве с одним меньшим измерением.
Представьте себе голограмму — плоскую двумерную поверхность, которая включает в себя трехмерное изображение. Подобным же образом, возможно, четырехмерная геометрия пространства-времени может быть закодирована в математике квантовой физики, работающей в трехмерном пространстве. Или, может быть, нужно больше измерений — а вот сколько измерений требуется, являются частью проблемы, которую нужно решить.
Квантовая запутанность – одна из сложнейших для понимания научных теорий
Во всяком случае, исследования в этом направлении открыли удивительную возможность: само пространство-время может быть порождено квантовой физикой, в частности загадочным явлением, известным как квантовая запутанность. Подробно о том, что представляет собой квантовая запутанность я рассказывала в этой статье.
Если попробовать объяснить более-менее простыми словами, то квантовая запутанность это сверхъестественная связь между частицами, разделенными огромными расстояниями. Испускаемые из общего источника, такие частицы остаются запутанными независимо от того, как далеко они друг от друга находятся. Если вы измерите свойство (например, спин) одной частицы, то узнаете, каким будет результат измерения спина другой частицы. Но до измерения эти свойства еще не определены, что противоречит здравому смыслу и подтверждается многими экспериментами. Кажется, что измерение в одном месте определяет, каким будет измерение в другом отдаленном месте.
Энергичные усилия нескольких физиков подарили миру теоретические доказательства того, что сети запутанных квантовых состояний плетут ткань пространства-времени. Эти квантовые состояния часто описываются как «кубиты» — биты квантовой информации. Запутанные кубиты создают сети с геометрией в пространстве с дополнительным измерением, выходящим за пределы числа измерений, в которых находятся кубиты. Таким образом, квантовую физику кубитов можно приравнять к геометрии пространства с дополнительным измерением.
Примечательно, что геометрия, созданная запутанными кубитами, может очень хорошо подчиняться уравнениям из общей теории относительности Эйнштейна, которые описывают движение под действием гравитации — по крайней мере, последние исследования указывают в этом направлении.
Подводя итог отмечу, что никто точно не знает, какие квантовые процессы в реальном мире ответственны за соткание ткани пространства-времени. Возможно, некоторые допущения, сделанные в уже имеющихся расчетах, окажутся ошибочными. Но вполне возможно, что физика стоит на пороге проникновения в основы природы глубже, чем когда-либо. В существование, содержащее ранее неизвестные измерения пространства и времени.
Пространственно-временной континуум
Космология
| Фундаментальные идеи |
|---|
| Специальная теория относительности Пространство-время Принцип эквивалентности Мировая линия · Псевдориманова геометрия |
| Явления |
|---|
| Задача двух тел в ОТО · Гравитационное линзирование · Гравитационные волны Увлечение инерциальных систем отсчёта · Расхождение геодезических Горизонт событий · Гравитационная сингулярность Чёрная дыра |
| Уравнения |
|---|
| Линеаризованная ОТО Параметризованный постньютоновский формализм Уравнения Эйнштейна |
| Развитие теории |
|---|
| Теории типа Калуцы — Клейна Квантовая гравитация Теории гравитации |
| Точные решения ОТО |
|---|
| Шварцшильда Райсснера — Нордстрёма · Керра Керра — Ньюмена · Решение Гёделя Казнера · Модель Милна · Фридмана — Леметра — Робертсона — Уолкера |
| Известные учёные |
|---|
| Эйнштейн · Минковский · Шварцшильд · Леметр · Эддингтон · Фридман · Робертсон · Керр · Чандрасекар · Хокинг и другие… |
Простра́нство-вре́мя — физическая модель, дополняющая пространство временны́м измерением и, таким образом, создающая новую теоретико-физическую конструкцию, которая называется пространственно-временным континуумом. В соответствии с теорией относительности, Вселенная имеет три пространственных измерения и одно временное измерение.
Количество измерений, необходимых для описания Вселенной, окончательно не определено. Теория струн, например, требовала наличия 10, а теперь даже 11 измерений (в рамках М-теории). Предполагается, что дополнительные (ненаблюдаемые) 6 или 7 измерений свёрнуты до планковских размеров, так что экспериментально они пока не могут быть обнаружены. Ожидается, тем не менее, что эти измерения каким-то образом проявляют себя в макроскопическом масштабе.
Первый вариант модели естественного объединения пространства и времени, пространство Минковского, был создан Германом Минковским в 1908 году [2] на основе специальной теории относительности Эйнштейна.
Несмотря на то, что, на первый взгляд, временное измерение абстрактно, понятие времени как измерения вполне конкретно. Когда мы хотим с кем-то встретиться, мы говорим, где «в пространстве» мы рассчитываем встретиться с ним, например, на 9-м этаже здания на углу Верхней Полевой улицы и шоссе Энтузиастов. В этом описании содержатся три элемента информации (9-й этаж, Верхняя полевая улица, шоссе Энтузиастов), описывающих конкретное место в трёх пространственных измерениях Вселенной. Не менее важным является указание времени встречи, например, в 3 часа пополудни. Эта часть информации указывает, где «во времени» состоится встреча. Следовательно, события описываются четырьмя элементами информации: тремя, указывающими расположение в пространстве, и одним, указывающим положение во времени. Таким образом характеризуется положение события в пространстве и времени, то есть в пространстве-времени. В этом смысле время представляет собой ещё одно измерение.
Пространство-время
Математическая формулировка
Космология
| Фундаментальные принципы |
|---|
| Специальная теория относительности · Пространство-время · Принцип эквивалентности · Мировая линия · Псевдориманова геометрия |
| Явления |
|---|
| Задача Кеплера в ОТО · Гравитационное линзирование · Гравитационные волны · Увлечение инерциальных систем отсчёта · Расхождение геодезических · Горизонт событий · Гравитационная сингулярность · Чёрная дыра |
| Уравнения |
|---|
| Уравнения Эйнштейна · Линеаризованная ОТО · Постньютоновский формализм |
| Развитие теории |
|---|
| Параметризованный постньютоновский формализм · Теории типа Калуцы — Клейна · Квантовая гравитация · Альтернативные теории |
| Решения |
|---|
| Шварцшильда · Райсснера — Нордстрёма · Керра · Керра — Ньюмена · Гёделя · Казнера · Фридмана — Леметра — Робертсона — Уолкера Приближённые решения: Постньютоновский формализм · Ковариантная теория возмущений · Численная относительность |
| Журналы |
|---|
| General Relativity and Gravitation · Classical and Quantum Gravity · Гравитация и космология · Living Reviews in Relativity |
| Известные учёные |
|---|
| Эйнштейн · Минковский · Шварцшильд · Леметр · Эддингтон · Фридман · Робертсон · Фок · Керр · Чандрасекар · Пенроуз Хокинг и другие… |
Простра́нство-вре́мя (простра́нственно-временно́й конти́нуум) — физическая модель, дополняющая пространство равноправным [1] временны́м измерением и таким образом создающая теоретико-физическую конструкцию, которая называется пространственно-временным континуумом.
В соответствии с теорией относительности, Вселенная имеет три пространственных измерения и одно временное измерение, и все четыре измерения органически связаны в единое целое, являясь почти равноправными и в определенных рамках (см. примечания ниже) способными переходить друг в друга при смене наблюдателем системы отсчёта.
В рамках общей теории относительности пространство-время имеет и единую динамическую природу, а его взаимодействие со всеми остальными физическими объектами (телами, полями) и есть гравитация. Таким образом, теория гравитации в рамках ОТО и других метрических теорий гравитации есть теория пространства-времени, полагаемого не плоским, а способным динамически менять свою кривизну.
Пространство-время непрерывно и с математической точки зрения представляет собой многообразие с лоренцевой метрикой.
Содержание
Современные представления
Первый развёрнутый вариант модели естественного объединения пространства и времени, пространство Минковского, был создан Германом Минковским в 1908 году [2] на основе специальной теории относительности Эйнштейна, а несколько ранее (в 1905 году), ключевое продвижение на этом пути сделал Анри Пуанкаре, заложивший основы четырехмерного пространственно-временного формализма.
Ключевым математическим отличием пространства-времени (пространства Минковского, или, в случае общей теории относительности — четырехмерного многообразия с лоренцевой метрикой) от обычного евклидова 4-мерного пространства является то, что при вычислении расстояния (интервала) квадраты значений разностей времени и длин пространственных координат берутся с противоположными знаками (в обычном пространстве соответствующие значения равноправны для любой оси координат и имеют одинаковый знак). Из этого вытекает следующее: прямая между двумя точками этого континуума (под прямой понимается движение по инерции) даёт максимальную продолжительность собственного времени (интервала). Для пространственной же длины прямая — это минимальная, а не максимальная величина.
В контексте теории относительности время неотделимо от трёх пространственных измерений и зависит от скорости наблюдателя [4] (см. собственное время).
Концепция пространства-времени сыграла исторически ключевую роль в создании геометрической теории гравитации. В рамках общей теории относительности гравитационное поле сводится к проявлениям геометрии четырехмерного пространства-времени, которое в этой теории не является плоским (гравитационный потенциал в ней отождествлен с метрикой пространства-времени).
Количество измерений, необходимых для описания Вселенной, окончательно не определено. Теория струн (суперструн), например, требовала наличия 10 (считая время), а теперь даже 11 измерений (в рамках М-теории). Предполагается, что дополнительные (ненаблюдаемые) 6 или 7 измерений свёрнуты (компактифицированы) до планковских размеров, так что экспериментально они пока не могут быть обнаружены. Ожидается, тем не менее, что эти измерения каким-то образом проявляют себя в макроскопическом масштабе. В самом старом — бозонном — варианте теория струн требует 26-мерного объемлющего пространства-времени; предполагается, что «лишние» измерения этой теории также должны или могут быть компактифицированы сперва до 10, сводясь таким образом к теории суперструн, а потом уже, как упомянуто здесь чуть выше, до 4 обычных измерений.
Временного континуума что это
Простра́нство-вре́мя (простра́нственно-временно́й конти́нуум) — физическая модель, дополняющая пространство равноправным[1] временны́м измерением и таким образом создающая теоретико-физическую конструкцию, которая называется пространственно-временным континуумом.
В соответствии с теорией относительности, Вселенная имеет три пространственных измерения и одно временное измерение, и все четыре измерения органически связаны в единое целое, являясь почти равноправными и в определенных рамках (см. примечания ниже) способными переходить друг в друга при смене наблюдателем системы отсчёта.
В рамках общей теории относительности пространство-время имеет и единую динамическую природу, а его взаимодействие со всеми остальными физическими объектами (телами, полями) и есть гравитация. Таким образом, теория гравитации в рамках ОТО и других метрических теорий гравитации есть теория пространства-времени, полагаемого не плоским, а способным динамически менять свою кривизну.
Пространство-время непрерывно и с математической точки зрения представляет собой многообразие с лоренцевой метрикой.
Континнуум это одно из выражений бесконечности. Причем, непрерывной бесконечности..Слияние трех измерений пространства и одного измерения времени в единый четырехмерный
Так называется среда, в которой разворачивается вселенная. Вроде как водичка, в которой плавают рыбки.
Звено,удерживающее настоящее между прошлым и будущим,или граница между паралельными мирами.
это математическая модель, абстракция, с помощью которой люди пытаются описать реальность.
а полегче вопрос нельзя?)я где то в фильме слышал такое))а так не знаю что это.
Фантастический термин характерезующий связь между временем и пространством
почитай Откровения людям Нового века, найдешь ответы на все важные вопросы.
Это что-то вроде точки пересечения пространства и времени
точка в пространстве, где возможен переход в другое время
ЭТО ПОРТАЛ МЕЖДУ БУДУШИМ И ПРОШЛЫМ ИЛИ МЕЖДУ МИРАМИ
я бы тебе сказал. если бы знал что такое континиум
Пространственно-временной континуум
«Французская революция началась в Париже 14 июля 1789 года». В этом предложении установлены место и время события. Тому, кто слышит это утверждение впервые и кто не знает, что значит Париж, можно было бы сказать: это город на нашей Земле, расположенный на 2° восточной долготы и 49° северной широты. Два числа характеризовали бы тогда место, а 14 июля 1789 года — время, в которое произошло событие. В физике точная характеристика, когда и где произошло событие, чрезвычайно важна, гораздо важнее, чем в истории, так как эти числа образуют основу количественного описания.
Ради простоты мы рассматривали прежде только движение вдоль прямой. Нашей координатной системой был твердый стержень с началом, но без конца. Сохраним это ограничение. Отметим на стержне различные точки; положение каждой из них может быть охарактеризовано только одним числом — координатой точки. Говоря, что координата точки равна 7,586 м, мы подразумеваем, что ее расстояние от начала стержня равно 7,586 м. Наоборот, если кто-то задает мне любое число и единицу измерения, я всегда могу найти точку на стержне, соответствующую этому числу. Мы видим, что каждому числу соответствует определенная точка на стержне, а каждой точке соответствует определенное число. Этот факт выражается математиками в следующем предложении:
Все точки стержня образуют одномерный континуум.
Тогда существует точка, сколь угодно близкая к данной точке стержня. Мы можем связать две отдаленные точки на стержне рядом отрезков, расположенных один за другим, каждый из которых сколь угодно мал. Таким образом, тот факт, что эти отрезки, связывающие отдаленные точки, могут быть взяты сколь угодно малыми, является характеристикой континуума.
Возьмем другой пример. Пусть мы имеем плоскость или, если вы предпочитаете что-либо более конкретное, поверхность прямоугольного стола (рис. 66). Положение точки на этом столе можно охарактеризовать двумя числами, а не одним, как раньше. Два числа суть расстояния от двух перпендикулярных краев стола. Не одно число, а пара чисел соответствует каждой точке плоскости; каждой паре чисел соответствует определенная точка. Другими словами, плоскость есть двумерный континуум. Тогда существуют точки, сколь угодно близкие к данной точке плоскости. Две отдаленные точки могут быть связаны кривой, разделенной на отрезки, сколь угодно малые. Таким образом, произвольная малость отрезков, последовательно укладывающихся на кривой, связывающей две отдаленные точки, каждая из которых может быть определена двумя числами, снова является характеристикой двумерного континуума.
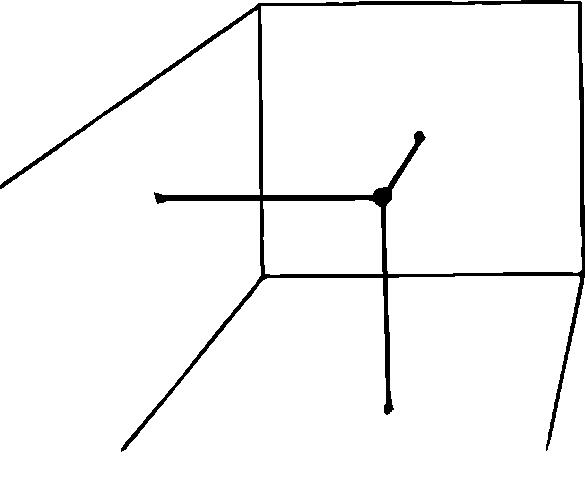
Еще один пример. Представим себе, что вы хотите в качестве системы координат рассматривать свою комнату. Это означает, что вы хотите любое положение тела определить относительно стен комнаты. Положение центра лампы, если она в покое, может быть описано тремя числами: два из них определяют расстояние от двух перпендикулярных стен, а третье — расстояние от пола или потолка. Каждой точке пространства соответствуют три определенных числа; каждым трем числам соответствует определенная точка в пространстве (рис. 67). Это выражается предложением:
Наше пространство есть трехмерный континуум.
Существуют точки, весьма близкие к каждой данной точке пространства. И опять произвольная малость отрезков линии, связывающей отдаленные точки, каждая из которых представлена тремя числами, есть характеристика трехмерного континуума.
Но все это едва ли относится к физике. Чтобы вернуться к физике, нужно рассмотреть движение материальных частиц. Чтобы исследовать и предсказывать явления в природе, необходимо рассматривать не только место, но и время физических событий. Возьмем снова простой пример.
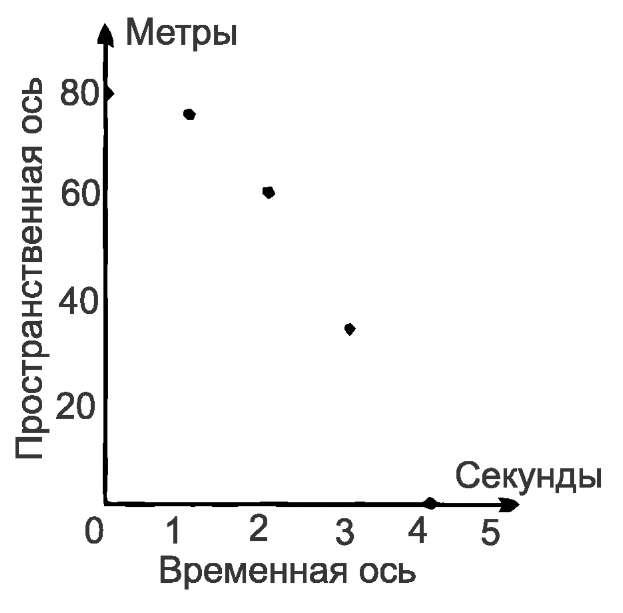
Маленький камешек, который примем за частицу, падает с башни. Допустим, что высота башни равна 80 м. Со времен Галилея мы в состоянии предсказать координаты камня в произвольный момент времени после начала его падения. Ниже представлено «расписание», приближенно описывающее положение камня после 1, 2, 3 и 4 секунд.
Время, с Высота над землёй, м 0 80 1 75 2 60 3 35 4 0
Те сведения, которые записаны в «расписании», можно было бы представить иначе. Пять пар чисел его можно было бы представить как пять точек на плоскости. Установим сначала масштаб. Например: пусть один отрезок будет изображать метр, а другой секунду (рис. 68).
Затем начертим две перпендикулярные линии; одну из них, скажем горизонтальную, назовем временно?й осью, вертикальную же — пространственной осью. Мы сразу же видим, что наше «расписание» можно представить пятью точками в пространственно-временно?й плоскости (рис. 69).
Расстояния точек от пространственной оси представляют собой координаты времени, указанные в первой колонке «расписания», а расстояния от временно?й оси — их пространственные координаты.
Одна и та же связь выражена двумя способами — с помощью «расписания» и точками на плоскости. Одно может быть построено из другого. Выбор между этими двумя представлениями является лишь делом вкуса, ибо в действительности они оба эквивалентны.
Сделаем теперь еще один шаг. Представим себе улучшенное «расписание», дающее положения не для каждой секунды, а, скажем, для каждой сотой или тысячной доли секунды. Тогда у нас будет много точек в нашей пространственно-временно?й плоскости. Наконец, если положение дается для каждого мгновения или, как говорят математики, если пространственная координата дается как функция времени, то совокупность точек становится непрерывной линией. Поэтому наш следующий рисунок (рис. 70) дает не отрывочные сведения, как прежде, а полное представление о движении камня.
Движение вдоль твердого стержня (башни), т. е. движение в одномерном пространстве, представлено здесь в виде кривой в двумерном пространственно-временно?м континууме. Каждой точке в нашем пространственно-временно?м континууме соответствует пара чисел, одно из которых отмечает временну?ю, а другое — пространственную координату. Наоборот, определенная точка в нашем пространственно-временно?м континууме соответствует некоторой паре чисел, характеризующей событие. Две соседние точки представляют собой два события, происшедших в местах, близких друг от друга, и в моменты времени, непосредственно следующие друг за другом.
Вы могли бы возразить против нашего способа представления следующим образом: мало смысла в том, чтобы представлять время отрезками и механически соединять его с пространством, образуя двумерный континуум из двух одномерных континуумов. Но тогда вы должны были бы столь же серьезно протестовать против всех графиков, представляющих, например, изменение температуры в Нью-Йорке в течение последнего лета, или против графиков, изображающих изменение стоимости жизни за последние несколько лет, так как в каждом из этих случаев употребляется тот же самый метод. В температурных графиках одномерный температурный континуум соединяется с одномерным временны?м континуумом в двумерный температурно-временной континуум.
Вернемся к частице, падающей с 80-метровой башни. Наша графическая картина движения есть полезное соглашение, так как она позволяет нам характеризовать положение частицы в любой произвольный момент времени. Зная, как движется частица, мы хотели бы изобразить ее движение еще раз. Сделать это можно двумя путями.
Вспомним изображение частиц, изменяющих свое положение со временем в одномерном пространстве. Мы изображаем движение как ряд событий в одномерном пространственном континууме. Мы не смешиваем время и пространство, применяя динамическую картину, в которой положения изменяются со временем.
Но можно изобразить то же самое движение другим путем. Мы можем образовать статическую картину, рассматривая кривую в двумерном пространственно-временно?м континууме. Теперь движение рассматривается как нечто заданное, существующее в двумерном пространственно-временно?м континууме, а не как нечто, изменяющееся в одномерном пространственном континууме.
Обе эти картины совершенно равноценны, и предпочтение одной из них перед другой есть лишь дело соглашения и вкуса.
То, что здесь сказано о двух картинах движения, не имеет отношения к теории относительности. Оба представления могут быть использованы с одинаковым правом, хотя классическая теория скорее предпочитала динамическую картину описания движения как того, что происходит в пространстве, статической картине, описывающей его в пространстве-времени. Но теория относительности изменила этот взгляд. Она явно предпочла статическую картину и нашла в этом представлении движения как того, что существует в пространстве-времени, более удобную и более объективную картину реальности. Мы должны еще ответить на вопрос, почему эти две картины эквивалентны с точки зрения классической физики и не эквивалентны с точки зрения теории относительности. Ответ будет понятным, если снова рассмотреть две системы координат, движущиеся прямолинейно и равномерно друг относительно друга.
Но мы уже убедились в том, что классические преобразования не могут применяться в физике в общем случае. С практической точки зрения они еще пригодны для малых скоростей, но не годятся для обоснования фундаментальных физических вопросов.
Согласно теории относительности, момент соударения камня с землей не будет одним и тем же для всех наблюдателей. И временна?я, и пространственная координата будут различными в двух различных системах координат, и изменение временно?й координаты будет весьма заметным, если относительная скорость систем приближается к скорости света. Двумерный континуум не может быть разбит на два одномерных континуума, как в классической физике. Мы не можем рассматривать пространство и время раздельно при определении пространственно-временны?х координат в другой системе координат. Разделение двумерного континуума на два одномерных оказывается с точки зрения теории относительности произвольным процессом, не имеющим объективного смысла.
Все, что мы только что сказали, нетрудно обобщить для случая движения, не ограниченного прямой линией. В самом деле, для описания событий в природе нужно применить не два, а четыре числа. Физическое пространство, постигаемое через объекты и их движения, имеет три измерения, и положения объектов характеризуются тремя числами. Момент события есть четвертое число. Каждому событию соответствует четыре определенных числа; каким-либо четырем числам соответствует определенное событие. Поэтому мир событий образует четырехмерный континуум. В этом нет ничего мистического, и последнее предложение одинаково справедливо и для классической физики, и для теории относительности. И опять различие обнаруживается лишь тогда, когда рассматриваются две системы координат, движущиеся друг относительно друга. Пусть движется комната, а наблюдатели внутри и вне ее определяют пространственно-временны?е координаты одних и тех же событий. Сторонник классической физики разобьет четырехмерный континуум на трехмерное пространство и одномерный временно?й континуум. Старый физик заботится только о преобразовании пространства, так как время для него абсолютно. Он находит разбиение четырехмерного мирового континуума на пространство и время естественным и удобным. Но с точки зрения теории относительности время, так же как и пространство, изменяется при переходе от одной системы координат к другой; при этом преобразования Лоренца выражают трансформационные свойства четырехмерного пространственно-временно?го континуума — нашего четырехмерного мира событий.
Мир событий может быть описан динамически с помощью картины, изменяющейся во времени и набросанной на фоне трехмерного пространства. Но он может быть также описан посредством статической картины, набросанной на фоне четырехмерного пространственно-временно?го континуума. С точки зрения классической физики обе картины, динамическая и статическая, равноценны. Но с точки зрения теории относительности статическая картина более удобна и более объективна.
Даже в теории относительности мы можем еще употреблять динамическую картину, если мы ее предпочитаем. Но мы должны помнить, что это деление на время и пространство не имеет объективного смысла, так как время больше не является «абсолютным». Дальше мы еще будем пользоваться «динамическим», а не «статическим» языком, но при этом всегда будем учитывать его ограниченность.
Данный текст является ознакомительным фрагментом.