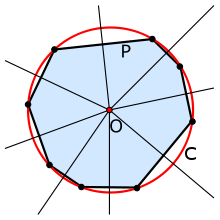
вокруг чего можно описать окружность
Описанная окружность (ЕГЭ 2022)
Первый вопрос, который может возникнуть: описанная – вокруг чего?
Ну, вообще-то иногда бывает и вокруг чего угодно, а мы будем рассуждать об окружности, описанной вокруг (иногда ещё говорят «около») треугольника.
Описанная окружность — коротко о главном
Определение
Окружность, описанная около треугольника – это окружность, которая проходит через все три вершины этого треугольника.
Центр описанной окружности
Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Радиус описанной окружности
Обрати внимание: теорема синусов сообщает, что для того чтобы найти радиус описанной окружности, нужна одна сторона (любая!) и противолежащий ей угол.
Расположение центра описанной окружности
В остроугольном треугольнике центр описанной окружности всегда лежит внутри треугольника
В тупоугольном треугольнике центр описанной окружности всегда лежит вне треугольника
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, а радиус равен половине гипотенузы.
Описанная окружность — подробнее
Определение
Описанная окружность – такая окружность, что проходит через все три вершины треугольника, около которого она описана.
Свойства и центр описанной кружности
И вот, представь себе, имеет место удивительный факт:
Вокруг всякого треугольника можно описать окружность.
Почему этот факт удивительный?
Потому что треугольники ведь бывают разные!
И для всякого найдётся окружность, которая пройдёт через все три вершины, то есть описанная окружность.
Доказательство этого удивительного факта мы приведем чуть позже, а здесь заметим только, что если взять, к примеру, четырехугольник, то уже вовсе не для всякого найдётся окружность, проходящая через четыре вершины.
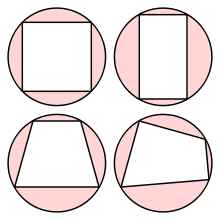
Вот, скажем, параллелограмм – отличный четырехугольник, а окружности, проходящей через все его четыре вершины – нет!
А есть только для прямоугольника:
Ну вот, а треугольник всякий и всегда имеет собственную описанную окружность! И даже всегда довольно просто найти центр этой окружности.
Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам этого треугольника.
Знаешь ли ты, что такое серединный перпендикуляр?
Серединный перпендикуляр — это прямая, проходящая через середину отрезка и перпендикулярная ему.
Прямая \( \displaystyle a\) – это серединный перпендикуляр к отрезку \( \displaystyle AB\).
А теперь посмотрим, что получится, если мы рассмотрим целых три серединных перпендикуляра к сторонам треугольника.
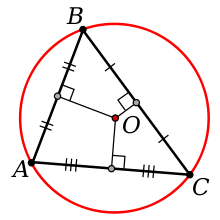
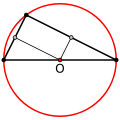
Вот оказывается (и это как раз и нужно доказывать, хотя мы и не будем), что все три перпендикуляра пересекутся в одной точке. Смотри на рисунок – все три серединных перпендикуляра пересекаются в одной точке \( \displaystyle O\).
Это и есть центр описанной около (вокруг) треугольника \( \displaystyle ABC\) окружности.
Как ты думаешь, всегда ли центр описанной окружности лежит внутри треугольника? Представь себе – вовсе не всегда!
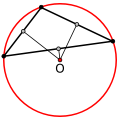
Если треугольник тупоугольный, то центр его описанной окружности лежит снаружи!
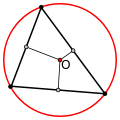
А вот если остроугольный, то внутри:
Что же делать с прямоугольным треугольником?
В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
Если треугольник – прямоугольный, то не надо строить аж три перпендикуляра, а можно просто найти середину гипотенузы – и центр описанной окружности готов!
Да ещё с дополнительным бонусом:
В прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.
Раз уж заговорили о радиусе описанной окружности: чему он равен для произвольного треугольника? И есть ответ на этот вопрос: так называемая теорема синусов.
В произвольном треугольнике:
\( \Large \displaystyle \frac<\sin \angle A>=2R\)
То есть чтобы найти радиус описанной окружности, нужно знать одну (!) сторону и один (!) противолежащий ей угол.
Хорошая формула? По-моему, просто отличная!
Доказательство теоремы
Теорема. Вокруг всякого треугольника можно описать окружность, при том единственным образом.
Центр этой окружности – точка пересечения серединных перпендикуляров к сторонам треугольника.
Давай наберёмся мужества и докажем эту теорему.
Если ты читал уже тему «Биссектриса» разбирался в том, почему же три биссектрисы пересекаются в одной точке, то тебе будет легче, но и если не читал – не переживай: сейчас во всём разберёмся.
Доказательство будем проводить, используя понятие геометрического места точек (ГМТ).
Геометрическое место точек, обладающих свойством «\( \displaystyle X\)» — такое множество точек, что все они обладают свойством «\( \displaystyle X\)» и никакие другие точки этим свойством не обладают.
Ну вот, например, является ли множество мячей – «геометрическим местом» круглых предметов? Нет, конечно, потому что бывают круглые …арбузы.
А является ли множество людей, «геометрическим местом», умеющих говорить? Тоже нет, потому что есть младенцы, которые говорить не умеют.
В жизни вообще сложно найти пример настоящего «геометрического места точек». В геометрии проще. Вот, к примеру, как раз то, что нам нужно:
Серединный перпендикуляр к отрезку является геометрическим местом точек, равноудалённых от концов отрезка.
Тут множество – это серединный перпендикуляр, а свойство «\( \displaystyle X\)» — это «быть равноудаленной (точкой) от концов отрезка».
Проверим? Итак, нужно удостовериться в двух вещах:
Проверим 1. Пусть точка \( \displaystyle M\) лежит на серединном перпендикуляре к отрезку \( \displaystyle AB\).
Соединим \( \displaystyle M\) с \( \displaystyle A\) и с \( \displaystyle B\).Тогда линия \( \displaystyle MK\) является медианой и высотой в \( \displaystyle \Delta AMB\).
Значит, \( \displaystyle \Delta AMB\) – равнобедренный, \( \displaystyle MA=MB\) – убедились, что любая точка \( \displaystyle M\), лежащая на серединном перпендикуляре, одинаково удалена от точек \( \displaystyle A\) и \( \displaystyle B\).
Теперь 2. Почти точно так же, но в другую сторону. Пусть точка \( \displaystyle M\) равноудалена от точек \( \displaystyle A\) и \( \displaystyle B\), то есть \( \displaystyle MA=MB\).
Возьмём \( \displaystyle K\) – середину \( \displaystyle AB\) и соединим \( \displaystyle M\) и \( \displaystyle K\). Получилась медиана \( \displaystyle MK\). Но \( \displaystyle \Delta AMB\) – равнобедренный по условию \( \displaystyle (MA=MB)\Rightarrow MK\) не только медиана, но и высота, то есть – серединный перпендикуляр. Значит, точка \( \displaystyle M\) — точно лежит на серединном перпендикуляре.
Всё! Полностью проверили тот факт, что серединный перпендикуляр к отрезку является геометрическим местом точек, равноудаленных от концов отрезка.
Это все хорошо, но не забыли ли мы об описанной окружности? Вовсе нет, мы как раз подготовили себе «плацдарм для нападения».
Описанная окружность
Теорема
| Около любого треугольника можно описать окружность. |
Доказательство
Дано: произвольный 
Доказать: около 
Доказательство:
1. Проведем серединные перпендикуляры к сторонам 
Точка О равноудалена от вершин 

Замечание 1
| Около треугольника можно описать только одну окружность. |
Доказательство
Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.
Замечание 2
| Около четырехугольника не всегда можно описать окружность. |
Доказательство
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.
Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
Доказательство
Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).
Верно и обратное утверждение:
Доказательство
Доказать: около АВСD можно описать окружность.
Доказательство:
Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.
Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).








Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).
Подставим (3) и (4) в (2), получим:
Примечание:
Окружность всегда можно описать:
Поделись с друзьями в социальных сетях:
Вокруг чего можно описать окружность
Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность
Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.
Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.
Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.
Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности
Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.
Окружность называется описанной около треугольника, если она проходит через три его вершины.
Окружность, вписанная в прямоугольный треугольник
Окружность, описанная около прямоугольного треугольника
Четырехугольник, вписанный в окружность
Окружность, вписанная в ромб
Описанная окружность
Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать 
Содержание
Свойства
Для треугольника
Обозначаем буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА = OB = ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.
Радиус
Радиус описанной окружности может быть найден по формулам



Где:





Положение центра описанной окружности
Пусть 

При этом 

Уравнение описанной окружности
Пусть 

Для точек 
Для четырехугольника
Вписанный простой (без самопересечений) четырёхугольник необходимо является выпуклым.
Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180° (π радиан).
Можно описать окружность около:
У четырёхугольника, вписанного в окружность, произведение длин диагоналей равно сумме произведений длин пар противоположных сторон: [1]
Для многоугольника
В сферическом треугольнике
Описанная окружность для сферического треугольника — это окружность, содержащая все его вершины.
См. также
Примечания
Литература
Полезное
Смотреть что такое «Описанная окружность» в других словарях:
Окружность — и её центр Окружность геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом. Содержание … Википедия
Окружность Аполония — Здесь собраны определения терминов из планиметрии. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф … Википедия
Окружность девяти точек — 9 точек Окружность девяти точек это окружность, проходящая через середины всех трёх сторон треугольника. Она также назы … Википедия
Окружность Эйлера — В геометрии треугольника окружность девяти точек это окружность, проходящая через середины всех трёх сторон треугольника. Она также называется окружностью Эйлера, окружностью Фейербаха, окружностью шести точек. Окружность девяти точек получила… … Википедия
Вписанная окружность — Окружность, вписанная в многоугольник ABCDE Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектри … Википедия
Вневписанная окружность — Вписанная (с центром I) и 3 вневписанные (с центрами в J) окружности в Вневписанная … Википедия
основная окружность конического зубчатого колеса с циклоидальной линией зубьев — Концентрическая окружность на развертке делительного конуса конического зубчатого колеса, при качении по которой другой окружности, называемой паллоидной, точка, жестко связанная с паллоидной окружностью, образует линию зуба в форме удлиненной… … Справочник технического переводчика
прилегающая окружность — Окружность минимального диаметра, описанная вокруг реального профиля наружной поверхности вращения, или окружность максимального диаметра, вписанная в реальный профиль внутренней поверхности вращения. Примечание В тех случаях, когда расположение… … Справочник технического переводчика
Основная окружность конического зубчатого колеса с циклоидальной линией зубьев — 163. Основная окружность конического зубчатого колеса с циклоидальной линией зубьев Концентрическая окружность на развертке делительного конуса конического зубчатого колеса, при качении по которой другой окружности, называемой паллоидной, точка,… … Словарь-справочник терминов нормативно-технической документации
начальная окружность ротора — Описанная вокруг оси технологического или транспортного ротора окружность, на которой расположены условные центры позиций ротора. [ГОСТ 14334 87] Тематики роторные и роторно конвейерные линии … Справочник технического переводчика