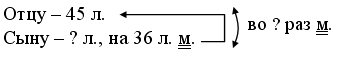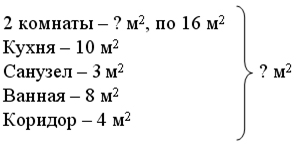во сколько раз одни единицы больше чем другие
Помогите учи ру! Во сколько раз одни единицы больше чем другие?
Ответ:
ориентируйся на вложения
,
,
Ответ:
Пошаговое объяснение:
,
,
Во сколько раз больше или меньше?
Победитель конкурса «Электронный учебник на уроке».
Цели: совершенствовать навыки решения задач на кратное сравнение; закреплять умения решать задачи с величинами «цена», «количество», «стоимость»; продолжить формирование вычислительных навыков; развивать внимание и мышление.
Ход урока
I. Организационный момент
II. Устный счет (работа в парах ЭФУ)
а) Длина бассейна – 8 м. Петя проплыл туда и обратно 4 раза. Сколько метров проплыл Петя?
б) Сколько шнурков нужно для 8 пар ботинок?
3. Геометрия на спичках.
а) Сколько всего на чертеже квадратов? Сколько на нем всего многоугольников?
б) Уберите одну палочку так, чтобы осталось 3 квадрата. Найдите несколько решений.
в) Уберите одну палочку так, чтобы осталось 2 квадрата. Найдите несколько решений.
г) Уберите две палочки так, чтобы осталось 3 квадрата. Найдите два решения и сравните их.
д) Уберите две палочки так, чтобы остался 1 квадрат. Какие еще остались многоугольники?
III. Сообщение темы урока
– Сегодня на уроке будем решать задачи с отношениями «на несколько больше (меньше)» и «в несколько раз больше (меньше)».
IV. Работа по теме урока
Задание № 8 (с. 66).
– Рассмотрите рисунок. Какие фигуры здесь изображены? (На нем изображены синий и красный отрезки.)
– На сколько частей точками разбит синий отрезок? (На 5 частей.)
– Выполните измерения и выясните, чему равна длина каждой такой части. (2 см.)
– Значит, синий отрезок разбит на 5 равных отрезков длиной 2 см. Измерьте длину красного отрезка. (Тоже 2 см.)
– Сколько раз красный отрезок будет «укладываться» в синем? (5 раз.)
– Делаем вывод: синий отрезок в 5 раз длиннее красного, а красный отрезок в 5 раз короче синего.
Задание № 9 (с. 66).
Это задание лучше выполнить фронтально.
· Если 28 больше 4 в 7 раз, то 4 меньше 28 в 7 раз.
· Если 56 больше 7 в 8 раз, то 7 меньше 56 в 8 раз и т. д.
Задание № 10 (с. 67).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Запишите кратко условие задачи.
– Что значит «Петя в 3 раза старше Сережи»?
Задание № 11 (с. 67).
– Рассмотрите рисунок в учебнике.
– Назовите самое высокое дерево. (Ель.)
– Во сколько раз ель выше рябины? (В 3 раза.)
– Во сколько раз рябина ниже ели? (В 3 раза.)
– Во сколько раз береза выше рябины? (В 2 раза.)
– Во сколько раз рябина ниже березы? (В 2 раза.)
Задание № 12 (с. 67).
– Что известно в задаче? Что требуется узнать?
– Запишите кратко условие задачи.
1) Сколько лет сыну?
2) Во сколько раз сын моложе отца?
Ответ: в 5 раз моложе.

V. Повторение пройденного материала
1. Работа по учебнику.
Задание № 25 (с. 70).
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи и решите ее с помощью выражения.
16 + 16 + 10 + 3 + 8 + 4 = 57 (м 2 ).
Задание № 26 (с. 70).
– Что известно? Что требуется узнать?
– Заполните таблицу по условию этой задачи.
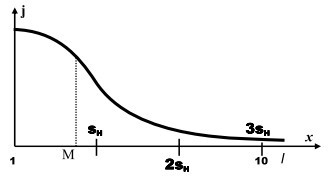
Для начала отметим, что понятие «несколько» применяется к величинам, имеющим очень большой разброс по абсолютной величине. Это могут быть единицы, десятки, тысячи, миллионы штук, или метры, километры, килограммы, тонны. Это могут быть и дробные величины, такие как сантиметры, миллиметры, литры, миллилитры, граммы, миллиграммы и т. д. Поскольку мы пользуемся позиционной системой счисления, то порядок величины может быть вынесен за скобки рассмотрения и служить простым размерным множителем для того отрезка, который мы оцениваем как «несколько». В этом случае удобно воспользоваться логарифмическими представлениями, т. е. использовать логарифмическую шкалу для представления величин. С учётом сказанного, приведём все величины к единому интервалу, базовую величину которого выберем равной основанию (M) используемой позиционной системы счисления. В привычной для нас десятичной системе счисления длина базового интервала будет равна 10 единицам. Он и будет служить нам осью х (смотри рисунок).
Теперь рассмотрим отмеченный выше феномен с инверсией направления изменения верхней границы интервала «несколько» при переходе к миллиону. Человек практически ежедневно и широко пользуется деньгами для покупки товаров и услуг. Наиболее часто он пользуется такими единицами как рубли, десятки и сотни рублей, реже тысячами. Количество людей, пользующихся в своей повседневной практике десятками тысяч рублей и более достаточно мало. Тогда можно проследить следующую тенденцию. Чем выше повседневная потребительская значимость денежной купюры для человека, тем ближе для неё устанавливаются границы значения «несколько» к их математически точному значению. Поскольку миллион для обычного потребителя не является повседневной купюрой, то его повседневная потребительская значимость для человека более абстракция, чем реальность. В этом случаи и границы понятия «несколько» для миллиона устанавливаются скорее как для абстрактного, чем реального объекта, поэтому и оказываются завышенными. А мы-то считали, что ведём опрос на отвлечённых, абстрактных числах и понятиях, а всё свелось подспудно к обыденным денежным знакам, с которыми мы оперируем повседневно. Это следует учитывать при проведении опросов и, особенно, при интерпретации полученных результатов.
Приведённые выше рассуждения о границах понятия «несколько» можно применить к позиционным системам счисления с произвольным основанием. Воспользуемся широко распространённой в вычислительной технике 16-ричной системой счисления. В этом случае длина базового интервала будет равна 16 единицам (от 1 до 16) и поэтому в рассуждениях необходимо использовать логарифмические представления так же по основанию 16. Для функции распределения исходными параметрами будут х0 = 1, sн = 5, тогда математическое ожидание величины «несколько» равно 0,7979sн = 3,9895; дисперсия равна 0,3634(sн)2 = 9,0850; s = 0,6028sн = 3,0140. При переходе от логарифмического к обычному представлению (не забудем, что логарифм берётся по основанию 16), ответ на поставленный в заголовке материала вопрос будет следующим: понятие «несколько» для 16-ричной системы счисления лежит в диапазоне от 2 до 6. Для системы счисления по основанию 8 (ещё одна система счисления, применяемая в вычислительной технике) получим следующий ответ: от 2 до 3.
Таким образом, можно сказать, что понятие «несколько» для:
16-ричной системы счисления лежит в диапазоне от 2 до 6;
10-тичной системы счисления в диапазоне от 2 до 4;
Журнал «Современные наукоемкие технологии» 2009. №4