внутренний угол шестиугольника чему равен
Гексагон
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
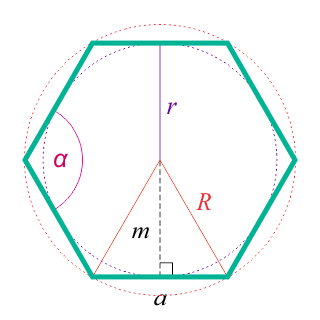
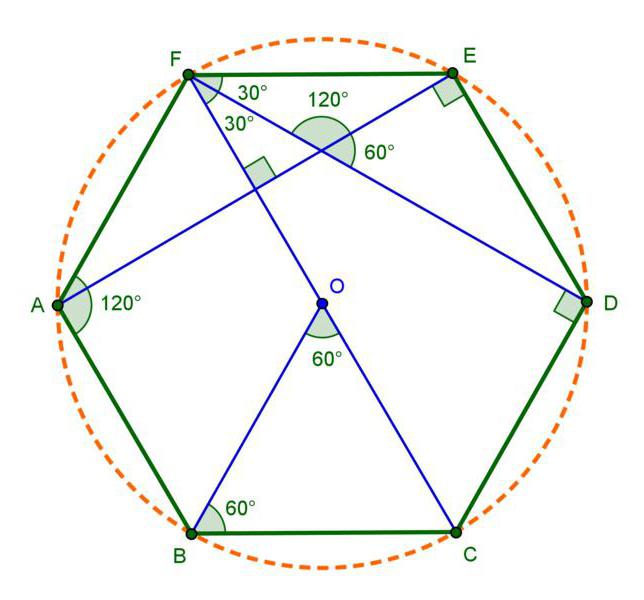
Внутренние углы Внутренние углы в правильном шестиугольнике равны \(120^\circ\) :
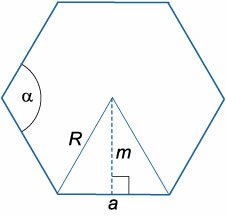
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
\(r = m = a\large\frac<<\sqrt 3 >><2>\normalsize\)
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
\(S = pr =
где \(p\) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Большая диагональ правильного шестиугольника
Правильным шестиугольником называется шестиугольник, у которого все стороны и углы равны. Правильный шестиугольник обладает следующими свойствами.
– Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
– Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.
– Меньшая диагональ правильного шестиугольника в раз больше его стороны.
– Угол между сторонами правильного шестиугольника равен 120°.
– Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
– Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.
Шестиугольник – это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.
Выпуклый шестиугольник – это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.
Правильный шестиугольник – это шестиугольник, все стороны которого равны между собой.
Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 – 2 ) = 720 градусов.
При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.
Свойства правильного шестиугольника
Внутренние углы Внутренние углы в правильном шестиугольнике равны (120^circ) :
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac >
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
Периметр правильного шестиугольника
Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны
(S = pr = largefrac >
ormalsize),
где (p) − полупериметр шестиугольника.
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности
Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности
Правильным шестиугольником называется выпуклый многоугольник с шестью одинаковыми сторонами и шестью углами.
Внутренние углы в правильном шестиугольнике равны (120^circ):
(alpha = 120^circ)
Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)
(m = alargefrac >
ormalsize)
Радиус вписанной окружности правильного шестиугольника равен апофеме:
(r = m = alargefrac >
ormalsize)
Радиус описанной окружности равен стороне правильного шестиугольника:
(R = a)
Периметр правильного шестиугольника
(P = 6a)
Площадь правильного шестиугольника
(S = pr = largefrac >
ormalsize),
где (p) − полупериметр шестиугольника.
Самая известная фигура, у которой больше четырех углов — это правильный шестиугольник. В геометрии он часто используется в задачах. А в жизни именно такой вид имеют соты на срезе.
Чем он отличается от неправильного?
Во-первых, шестиугольником является фигура с 6 вершинами. Во-вторых, он может быть выпуклым или вогнутым. Первый отличается тем, что четыре вершины лежат по одну сторону от прямой, проведенной через две другие.
В-третьих, правильный шестиугольник характеризуется тем, что все его стороны равны. Причем каждый угол фигуры тоже имеет одинаковое значение. Чтобы определить сумму всех его углов, потребуется воспользоваться формулой: 180º * (n — 2). Здесь n — число вершин фигуры, то есть 6. Простой расчет дает значение в 720º. То есть каждый угол равен 120 градусам.
В повседневной деятельности правильный шестиугольник встречается в снежинке и гайке. Химики видят ее даже в молекуле бензола.
Какие свойства требуется знать при решении задач?
К тому, что указано выше, следует добавить:
Введенные обозначения
Традиционно сторона правильной геометрической фигуры обозначается латинской буквой «а». Для решения задач требуются еще площадь и периметр, это S и P соответственно. В правильный шестиугольник бывает вписана окружность или описана около него. Тогда вводятся значения для их радиусов. Обозначаются они соответственно буквами r и R.
В некоторых формулах фигурируют внутренний угол, полупериметр и апофема (являющаяся перпендикуляром к середине любой стороны из центра многоугольника). Для них используются буквы: α, р, m.
Формулы, которые описывают фигуру
Для расчета радиуса вписанной окружности потребуется такая: r = (a * √3) / 2, причем r = m. То есть такая же формула будет и для апофемы.
Поскольку периметр шестиугольника — это сумма всех сторон, то он определится так: P = 6 * a. С учетом того, что сторона равна радиусу описанной окружности, для периметра существует такая формула правильного шестиугольника: P = 6 * R. Из той, что приведена для радиуса вписанной окружности, выводится зависимость между а и r. Тогда формула принимает такой вид: Р = 4 r * √3.
Для площади правильного шестиугольника может пригодиться такая: S = p * r = (a 2 * 3 √3) / 2.
Задачи
№ 1. Условие. Имеется правильная шестиугольная призма, каждое ребро которой равно 4 см. В нее вписан цилиндр, объем которого необходимо узнать.
Решение. Объем цилиндра определяется как произведение площади основания на высоту. Последняя совпадает с ребром призмы. А она равна стороне правильного шестиугольника. То есть высота цилиндра — тоже 4 см.
Чтобы узнать площадь его основания, потребуется вычислить радиус вписанной в шестиугольник окружности. Формула для этого указана выше. Значит, r = 2√3 (см). Тогда площадь круга: S = π * r 2 = 3,14 * (2√3 ) 2 = 37,68 (см 2 ).
Осталось сосчитать объем: V = 37, 68 * 4 = 150,72 (см 3 ).
№ 2. Условие. Вычислить радиус окружности, которая вписана в правильный шестиугольник. Известно, что его сторона равна √3 см. Чему будет равен его периметр?
Решение. Эта задача требует использования двух из указанных формул. Причем их необходимо применять, даже не видоизменяя, просто подставить значение стороны и вычислить.
Таким образом, радиус вписанной окружности получается равным 1,5 см. Для периметра оказывается верным такое значение: 6√3 см.
Ответ. r = 1,5 см, Р = 6√3 см.
№ 3. Условие. Радиус описанной окружности равен 6 см. Какое значение в этом случае будет у стороны правильного шестиугольника?
Решение. Из формулы для радиуса вписанной в шестиугольник окружности легко получается та, по которой нужно вычислять сторону. Ясно, что радиус умножается на два и делится на корень из трех. Необходимо избавиться от иррациональности в знаменателе. Поэтому результат действий принимает такой вид: (12 √3) / (√3 * √3), то есть 4√3.
Правильный многоугольник
Правильный многоугольник — это многоугольник, все стороны и углы которого равны.
Вокруг правильного многоугольника можно описать окружность и в него можно вписать окружность. Центры этих окружностей совпадают.
Правильный шестиугольник
Правильный шестиугольник – это шестиугольник, все стороны и углы которого равны.
Описанный многоугольник
Шестиугольник, виды, свойства и формулы
Шестиугольник, виды, свойства и формулы.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
2. Все углы равны между собой и составляют 120°.
Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.
Рис. 5. Правильный шестиугольник
5. Количество диагоналей правильного шестиугольника равно 9.
Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.
Правильный шестиугольник
Содержание
Свойства
Построение
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Правильный шестиугольник в природе, технике и культуре
Примечания
Смотрите также
Ссылки
 |
 Правильные многоугольники Правильные многоугольники | |
|---|---|
| Основные | Треугольник • Квадрат • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Семнадцатиугольник • 257-угольник • 65537-угольник |
| См. также | Многоугольник • Теорема Гаусса — Ванцеля |
Полезное
Смотреть что такое «Правильный шестиугольник» в других словарях:
Шестиугольник — Правильный шестиугольник Шестиугольник многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы. Сумма внутренних углов выпуклого шестиугольника р … Википедия
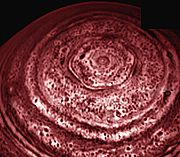
Шестиугольник Сатурна — Гексагональное устойчивое атмосферное образование на северном полюсе Сатурна, открытое аппаратом Вояджер 1 и наблюдаемое снова в 2006 году а … Википедия
Правильный семиугольник — Правильный семиугольник это правильный многоугольник с семью сторонами. Содержание … Википедия
Правильный треугольник — Правильный треугольник. Правильный (или равносторонний) треугольник это правильный многоугольник с тремя сторонами, первый из правильных многоугольников. Все стороны … Википедия
Правильный девятиугольник — это правильный многоугольник с девятью сторонами. Свойства Правиль … Википедия
Правильный 17-угольник — Правильный семнадцатиугольник геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание 1… … Википедия
Правильный семнадцатиугольник — геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание … Википедия
Правильный восьмиугольник — (октагон) геометрическая фигура из группы правильных многоугольников. У него восемь сторон и восемь углов и все углы и стороны равны между собой … Википедия
Правильный 65537-угольник — 65537 угольник или окружность? Правильный 65537 угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиугольник) геометрическая фигура из группы правильных многоугольников, состоящая из 65537 … Википедия
Шестиугольник, виды, свойства и формулы




Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник
Рис. 2. Невыпуклый шестиугольник
Сумма внутренних углов любого выпуклого шестиугольника равна 720°.
Размеры
Чтобы отвертка прослужила долго, и не стерлась, важно выбрать правильный размер инструмент с нужным наконечником.
Для каждого вида разработаны специальные стандарты размеров, и присвоены им номерные обозначения.
Шлицевые отвертки с плоской формой наконечника могут иметь ширину от 2 до 18 мм, а крестообразные модели идут с нумерацией от 0 до 4.
Все номерные виды рассчитаны на определенный диаметр наружной резьбы:
• № 0 – до двух мм; • № 1 – от двух до трех мм; • № 2 – от трех до пяти мм; • № 3 – от пяти до семи мм и т.д.
Размеры стержня зависят от номера отвертки.
Так, например, нулевая отвертка имеет диаметр стержня 4 миллиметра при длине до 80 миллиметров.
По мере возрастания номера увеличивается диаметр и длина стержня.
Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Углы правильного шестиугольника образуют шесть равносторонних треугольников.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Торцевые гаечные ключи
Этот вид ключей представляет собой полую трубку или цилиндр с углублениями на обоих концах. Торцевые ключи бывают двух типов:
Г-образные торцевые ключи
Они имеют одинаковый размер на обоих краях рабочих частей. Это сделано с тем расчетом, что гайка (или болт) могут находиться глубоко от поверхности и тогда используется длинная часть ключа, но при этом необходимо приложить больше усилий (из-за маленького рычага). Если деталь находится неглубоко, тогда используется короткая часть ключа, соответственно из-за большего рычага усилий прикладывается меньше.
I-образные гаечные ключи
Выглядят как полый цилиндр с рабочей частью разного размера на обоих концах. Работать таким ключом приходиться, используя рычаг (вороток) который вставляется в сквозное отверстие в корпусе ключа.
Виды молотков и их назначение
Шестигранные ключи
Этот вид ключей имеет Г-образную форму и используется для работы с болтами (шурупами, винтами) имеющими не внешние грани, а внутренние. В основном применяются в основном при сборке мебели, ремонте бытовой технике и подобных работах.



Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
a1 = a2 = a3 = a4= a5= a6.
2. Все углы равны между собой и составляют 120°.
α1 = α2 = α3 = α4 = α5 = α6 = 120°.
Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.
Рис. 5. Правильный шестиугольник
5. Количество диагоналей правильного шестиугольника равно 9.
Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.
Рис. 8. Правильный шестиугольник
Накидные ключи
У этих ключей рабочая часть имеет фору кольца с гранями на внутренней стороне. Его конструкция более надежна чем у рожковых ключей, так как деталь охватывается по всей поверхности (то есть как минимум в шести местах), что практически исключает деформацию углов. Накидные ключи существуют с двумя типами внутреннего профиля – с 6-и гранным профилем и 12-и гранным профилем. Профилем с 12-ю гранями работать в ограниченном пространстве удобней, так как ему достаточно поворота на 30 градусов, к ключу с 6-и гранным профилем необходимо 60 градусов поворота.
Чистый двор и дом — мойка высокого давления!
Более распространенны ключи с наклонной головкой, когда рабочая часть находится под небольшим углом к рукоятке. Накидные ключи выпускаются разного размера, как и рожковые ключи.
Правильный шестиугольник в природе, технике и культуре:
Пчелиные соты имеют форму правильного шестиугольника.
Графит, графен имеют гексагональную кристаллическую решетку.
Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.
Рис. 9. Гигантский гексагон на Сатурне
Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
Панцирь черепахи состоит из шестиугольников.
Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.
Рис. 10. Материковая часть Франции
Виды отверток и их назначение
Универсальная отвертка слесарная – это инструмент, который есть практически в каждом доме.
Благодаря отвертке можно выполнять ремонтные работы разной степени сложности, главное знать, какой тип и диаметр подойдет в каждом конкретном случае.
О том, какие бывают отвертки можно узнать, если детальнее углубиться в тему.
Отличительной особенностью всех видов является разное толщина стержня.
Читать также: Как проверить акб без нагрузочной вилки
Наиболее популярными считают отвертки с круглым и квадратным сечением, с прямым или крестообразным шлицем.
Однако технический прогресс не стоит на месте и наряду с новыми видами крепежа появляются профессиональные отвертки для вкручивания болтов, шурупов и прочих элементов.
Все это делается для того, чтобы облегчить работу потребителям.
• На данный момент кроме универсальных моделей существует еще несколько модернизированных видов отверток для проведения разных работ.
Например, переставная отвертка отличается своей универсальностью, т.к. с одной стороны стержня она плоская, а с другой крестовая.
Некоторые переставные модели имеют несколько разных наконечников, что повышает универсальность инструмента.
• Точная или как ее еще называют, тонкая отвертка – подойдет для ремонта мобильных телефонов, ее маркировка соответствует нулевому обозначению.
Изделие производят с малым размером шлица, не более 2мм, что позволяет выполнить точную работу с мелкими деталями.
• Особые эргономичные свойства приобрела двухкомпонентная отвертка, ее отличительной особенностью стала прочная рукоять из комбинированных материалов.
Для покрытия рукояти использовали полипропилен и резину.
Двухкомпонентное покрытие способствует надежному захвату, чтобы изделие уже не могло выскользнуть из рук.
• Для работы с тонкими деталями используют часовые отвертки, с их помощью ремонтируют часовые механизмы.
Размер наконечника изделия – не более миллиметра.
На этом классификация профессиональных монтажных отверток не заканчивается, существует еще много разновидностей моделей, предназначенных для определенных целей.
Формулы правильного шестиугольника:
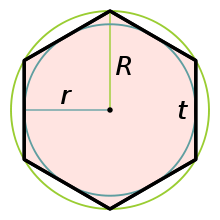
Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.
Формулы периметра правильного шестиугольника:
Формулы площади правильного шестиугольника:
Формула радиуса окружности, вписанной в правильный шестиугольник:
Формула радиуса окружности, описанной вокруг правильного шестиугольника:
Маркировка и размеры [ править | править код ]
Ключи и отвёртки имеют маркировку T
или
TX
с номером шлица — 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 20, 25, 27, 30, 40, 45, 50, 55, 60, 70, 80, 90, 100.
Ключи и отвёртки со шлицом Torx Tamper Resistant
после основной маркировки дополнительно обозначаются
TR
.
У ключей и отвёрток со шлицом Torx Plus
сначала указывается номер шлица, а после — вместо
T
или
TX
обозначается буквами
IP
.
Ключи и отвёртки со шлицом Torx Plus Tamper Resistant
после основной маркировки дополнительно обозначаются
TS
.
Размер определяется по диаметру окружности описанной по вершинам звездочки инструмента (для версии E — болта).
Приблизительные размеры и моменты затяжки [3]
| дюймы | мм | Н•м | ||
| T1 | 0,031″ | 0,81 | 0,02 — 0,03 | |
| T2 | 0,036″ | 0,93 | 0,07 — 0,09 | |
| T3 | 0,046″ | 1,10 | 0,14 — 0,18 | |
| T4 | 0,050″ | 1,28 | 0,22 — 0,28 | |
| T5 | 0,055″ | 1,42 | 0,43 — 0,51 | |
| T5.5 [4] [5] [6] | ||||
| T6 | 0,066″ | 1,70 | 0,75 — 0,90 | |
| T7 | 0,078″ | 1,99 | 1,4 — 1,7 | |
| T8 | 0,090″ | 2,31 | 2,2 — 2,6 | |
| T9 | 0,098″ | 2,50 | 2,8 — 3,4 | |
| T10 | 0,107″ | 2,74 | 3,7 — 4,5 | |
| T15 | 0,128″ | 3,27 | 6,4 — 7,7 | |
| T20 | 0,151″ | 3,86 | 10,5 — 12,7 | E4 |
| T25 | 0,173″ | 4,43 | 15,9 — 19 | E5 |
| T27 | 0,195″ | 4,99 | 22,5 — 26,9 | |
| T30 | 0,216″ | 5,52 | 31,1 — 37,4 | E6 |
| T35 [7] [8] [9] | ||||
| T40 | 0,260″ | 6,65 | 54,1 — 65,1 | E8 |
| T45 | 0,306″ | 7,82 | 86 — 103,2 | |
| T47 [10] [11] | GM-Style | |||
| T50 | 0,346″ | 8,83 | 132 — 158 | E10 |
| T55 | 0,440″ | 11,22 | 218 — 256 | E12 |
| T60 | 0,519″ | 13,25 | 379 — 445 | E16 |
| T70 | 0,610″ | 15,51 | 630 — 700 | E18 |
| T80 | 0,690″ | 17,54 | 943 — 1048 | E20 |
| T90 | 0,784″ | 19,92 | 1334 — 1483 | |
| T100 | 0,871″ | 22,13 | 1843 — 2048 | E24 |
Размеры внешних шлицов Torx
| Номер | Размер [12] | Стандартный болт [13] | ||
| дюймы | мм | SAE | метрический | |
| E4 | 0,15″ | 3,8 | #6 | M3 |
| E5 | 0,18″ | 4,7 | #8 | M4 |
| E6 | 0,22″ | 5,6 | #10 | M5 |
| E7 | 0,24″ | 6,1 | ||
| E8 | 0,29″ | 7,4 | 1/4″ | M6 & M7 |
| E10 | 0,36″ | 9,3 | 5/16″ | M8 |
| E12 | 0,43″ | 11,1 | 3/8″ | M10 & M11 |
| E14 | 0,50″ | 12,8 | 7/16″ | M12 |
| E16 | 0,57″ | 14,7 | 1/2″ | |
| E18 | 0,65″ | 16,6 | 9/16″ | M14 |
| E20 | 0,72″ | 18,4 | 5/8″ | M16 |
| E24 | 0,87″ | 22,1 | 3/4″ | M18 & M20 |
| E28 | 7/8″ | M22 | ||
| E32 | 1″ | M24 & M27 | ||
| E36 | 1-1/8″ | M30 | ||
| E40 | 1-1/4″ | M33 | ||
| E44 | 1-3/8″ | M36 | ||
Использование [ править | править код ]
Крепёж со шлицом Torx обычно используется в технике: автомобилях, велосипедах, тормозных системах, разнообразных сборных металлических конструкциях, жёстких дисках компьютеров, банкоматах, потребительской электронике и топливной аппаратуре.
Неизвестно, специально это было сделано или нет, но размеры Torx коррелируются с размерами инбусовых ключей и позволяют выкрутить сорванный шестигранный шлиц. При срыве шлица в образованное отверстие забивается инструмент Torx и практически со стопроцентным результатом позволяет выкрутить сорванный болт или винт.
Следует отметить, что при работе с Torx необходимо учитывать следующие особенности:
Несоблюдение этих правил зачастую ведёт к разрушению головки болта и, как следствие, к необоснованной критике Torx.